基于模塊度和均衡度的復(fù)雜產(chǎn)品架構(gòu)評價方法

魏云篷，陳永亮，索樹燦

（天津大學(xué)機(jī)械工程系，天津 300354）

通過對一定范圍內(nèi)的不同功能或相似功能的產(chǎn)品進(jìn)行功能分析，對產(chǎn)品進(jìn)行分解，建立通用的模塊系列，再選用模塊來組合出多樣化的新產(chǎn)品，以滿足市場多樣化需求的設(shè)計(jì)方法稱為模塊化設(shè)計(jì)[1]。同樣，通過模塊化設(shè)計(jì)產(chǎn)生的模塊的組合，可以進(jìn)一步表達(dá)產(chǎn)品架構(gòu)。產(chǎn)品架構(gòu)是綜合設(shè)計(jì)理論、軟件工程、運(yùn)作管理和產(chǎn)品開發(fā)管理等多學(xué)科的知識而形成的，是將產(chǎn)品功能分配給物理組件而形成的系統(tǒng)性方案[2]，體現(xiàn)了產(chǎn)品的分解和集成。產(chǎn)品的物理組件及其關(guān)系可以用復(fù)雜網(wǎng)絡(luò)表示。復(fù)雜網(wǎng)絡(luò)是現(xiàn)實(shí)世界中復(fù)雜系統(tǒng)的一種抽象表現(xiàn)形式。現(xiàn)實(shí)世界中存在很多類型的復(fù)雜網(wǎng)絡(luò)，例如社交網(wǎng)絡(luò)、技術(shù)網(wǎng)絡(luò)和神經(jīng)網(wǎng)絡(luò)等。Newman[3]于2002年提出了復(fù)雜網(wǎng)絡(luò)的“社團(tuán)結(jié)構(gòu)”概念。在隨后的幾年中，復(fù)雜網(wǎng)絡(luò)的研究受到了眾多學(xué)者的關(guān)注[4-5]。

產(chǎn)品模塊的劃分是模塊化設(shè)計(jì)的關(guān)鍵環(huán)節(jié)，國內(nèi)外學(xué)者對此進(jìn)行了大量研究。Tsai等[6]根據(jù)零件的幾何約束、機(jī)械強(qiáng)度、能量和信號建立相關(guān)度矩陣，并用制造和裝配的信息熵對產(chǎn)品模塊的劃分結(jié)果進(jìn)行評價。潘雙夏等[7]根據(jù)產(chǎn)品的客戶需求、幾何相關(guān)性和物理相關(guān)性建立相關(guān)度矩陣，并用裝配、成本、維修的信息熵對產(chǎn)品模塊的劃分結(jié)果進(jìn)行評價。王日君等[8]根據(jù)產(chǎn)品的功能相關(guān)性和結(jié)構(gòu)相關(guān)性建立相關(guān)度矩陣，并用橫系列設(shè)計(jì)復(fù)雜度、縱系列設(shè)計(jì)復(fù)雜度和更新?lián)Q代設(shè)計(jì)復(fù)雜度對模塊劃分結(jié)果進(jìn)行評價。李中凱等[9]根據(jù)產(chǎn)品的功能、結(jié)構(gòu)、壽命、材料和回收的相關(guān)性建立相關(guān)度矩陣，并用最小描述長度對模塊劃分結(jié)果進(jìn)行評價。毛保全等[10]提出了用設(shè)計(jì)制造的復(fù)雜度、成本和維修的信息熵對模塊劃分方案進(jìn)行評價的方法。呂健等[11]根據(jù)產(chǎn)品的功能相關(guān)性和結(jié)構(gòu)相關(guān)性建立相關(guān)度矩陣，并用設(shè)計(jì)復(fù)雜度、裝配復(fù)雜度、維護(hù)復(fù)雜度、更新升級復(fù)雜度和循環(huán)利用復(fù)雜度對模塊劃分結(jié)果進(jìn)行評價。李愛平等[12]根據(jù)客戶需求相關(guān)性矩陣、功能性矩陣、幾何相關(guān)性矩陣和物理相關(guān)性矩陣建立相關(guān)度矩陣，并用裝配復(fù)雜度、客戶參與變型設(shè)計(jì)的復(fù)雜度、模塊相對獨(dú)立性和模塊內(nèi)部元素的親密度對模塊劃分結(jié)果進(jìn)行評價。Gu等[13]提出了面向產(chǎn)品全生命周期的模塊劃分方法，根據(jù)產(chǎn)品生命周期各階段的目標(biāo)要求建立各相關(guān)矩陣，并由設(shè)計(jì)人員對以每個設(shè)計(jì)目標(biāo)為基礎(chǔ)得出的模塊劃分方案進(jìn)行比較，選出最佳方案。田楚楚[14]用模塊化程度和模塊化效益對模塊劃分方案進(jìn)行評價。陳永亮等[15]基于可適應(yīng)信息熵提出了產(chǎn)品可適應(yīng)度評價。還有學(xué)者用綜合評價方法從不同角度對模塊劃分方案進(jìn)行了評價[16-18]。

以上研究大多是建立產(chǎn)品不同要素之間的相關(guān)度矩陣，并用信息熵等單一指標(biāo)對模塊劃分結(jié)果進(jìn)行評價的。而對于復(fù)雜產(chǎn)品，由于其零部件眾多，以上方法可能不再適用。因此，筆者提出復(fù)雜產(chǎn)品的相關(guān)度矩陣建立方法和模塊劃分結(jié)果的評價方法。首先，介紹復(fù)雜產(chǎn)品相關(guān)度矩陣的建立方法；其次，提出復(fù)雜產(chǎn)品模塊劃分方案的綜合評價指標(biāo)；最后，以盾構(gòu)螺旋輸送機(jī)為例，利用層次聚類得到不同的模塊劃分方案，用提出的綜合評價指標(biāo)評價模塊劃分方案，并從中選出最優(yōu)方案，以此來得到螺旋輸送機(jī)的最優(yōu)產(chǎn)品架構(gòu)。

1 復(fù)雜產(chǎn)品相關(guān)度矩陣的建立

研發(fā)成本高、生產(chǎn)規(guī)模大、技術(shù)含量高、單件或小批量定制化、集成度高的大型產(chǎn)品，系統(tǒng)或基礎(chǔ)設(shè)施稱為復(fù)雜產(chǎn)品[19]。

1.1 復(fù)雜產(chǎn)品的網(wǎng)絡(luò)圖

復(fù)雜產(chǎn)品的零件之間存在著約束關(guān)系。當(dāng)產(chǎn)品的零件數(shù)n=6時，根據(jù)零件之間的關(guān)系可以建立復(fù)雜產(chǎn)品的網(wǎng)絡(luò)圖，如圖1（a）所示，其中存在頂點(diǎn)和邊兩種元素。設(shè)網(wǎng)絡(luò)圖為G，則：

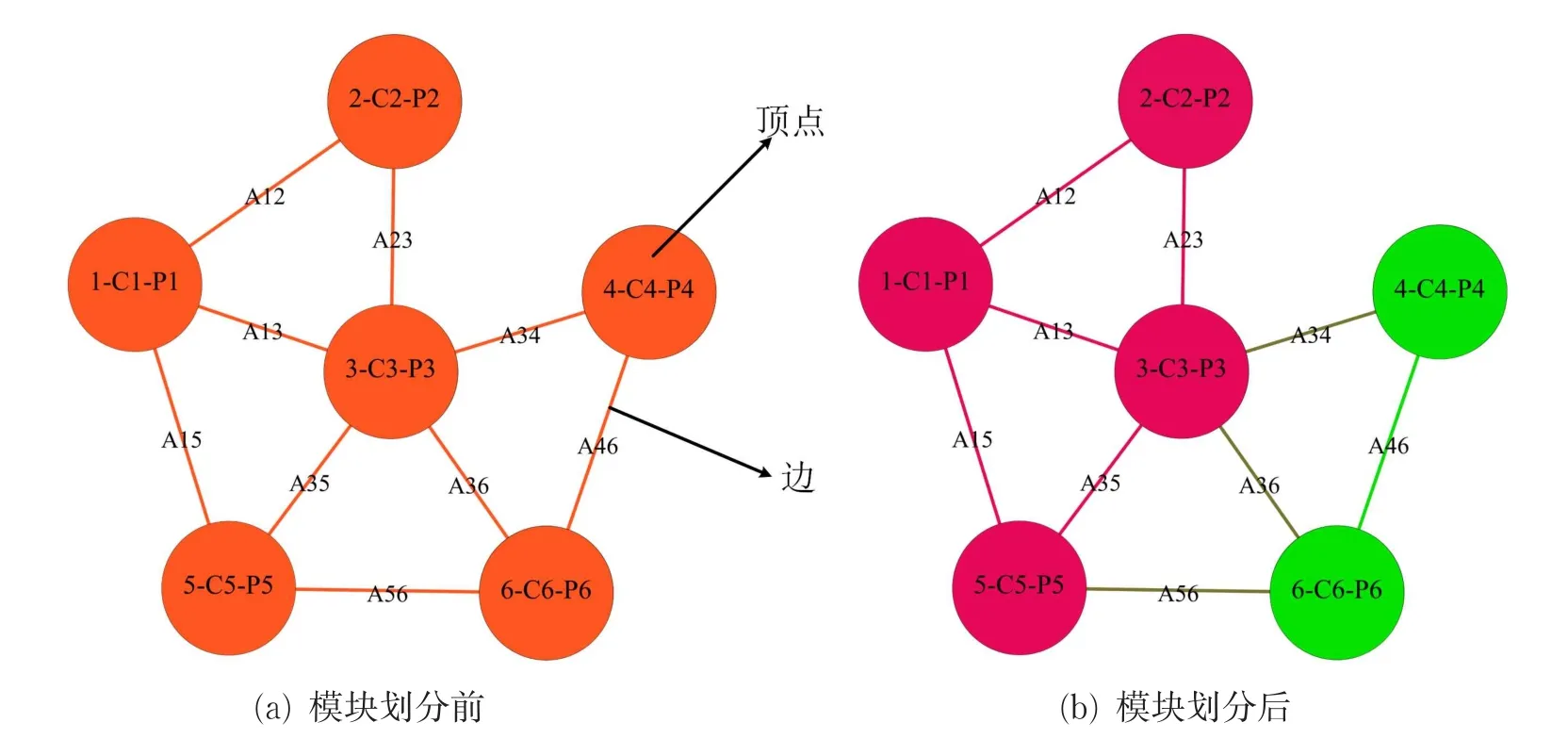
圖1 復(fù)雜產(chǎn)品網(wǎng)絡(luò)圖Fig.1 Network diagram of complex product

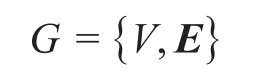
式中：V為頂集，包括組成產(chǎn)品的所有零件；E為邊集，包括所有零件之間的關(guān)系，即相關(guān)度矩陣。

一般地，當(dāng)產(chǎn)品有n個零件時，則：

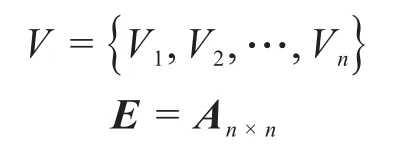
式中：A為產(chǎn)品的相關(guān)度矩陣。

同時，零件具有成本、復(fù)雜度屬性。設(shè)零件的屬性集為R，則：

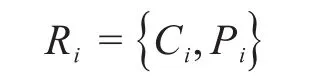
式中：Ri為零件i（i=1，2，…，n）的屬性集；Ci為零件i的成本；Pi為零件i的復(fù)雜度。

模塊劃分后的產(chǎn)品網(wǎng)絡(luò)圖如圖1（b）所示。共劃分為M1和M2兩個模塊，模塊1包含零件1，2，3，5，模塊2包含零件4，6，即：

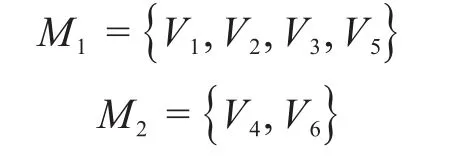
1.2 復(fù)雜產(chǎn)品的相關(guān)度矩陣

對于復(fù)雜產(chǎn)品，因其零件數(shù)量眾多，直接建立零件間的相關(guān)度矩陣比較困難，且大部分已有模塊劃分方案。因此，根據(jù)復(fù)雜產(chǎn)品已有的模塊劃分方案對產(chǎn)品的每個模塊建立相關(guān)度矩陣。假如產(chǎn)品由n個零件組成，已有劃分方案將產(chǎn)品劃分為m個模塊，則產(chǎn)品最終的相關(guān)度矩陣為An×n，每個模塊的相關(guān)度矩陣（子矩陣）為Ai(i=1，2，…，m)。將所有模塊的相關(guān)度矩陣構(gòu)造成分塊矩陣，再添加模塊間的相關(guān)度值即得到整個復(fù)雜產(chǎn)品的相關(guān)度矩陣。復(fù)雜產(chǎn)品相關(guān)度矩陣的建立過程如圖2所示。

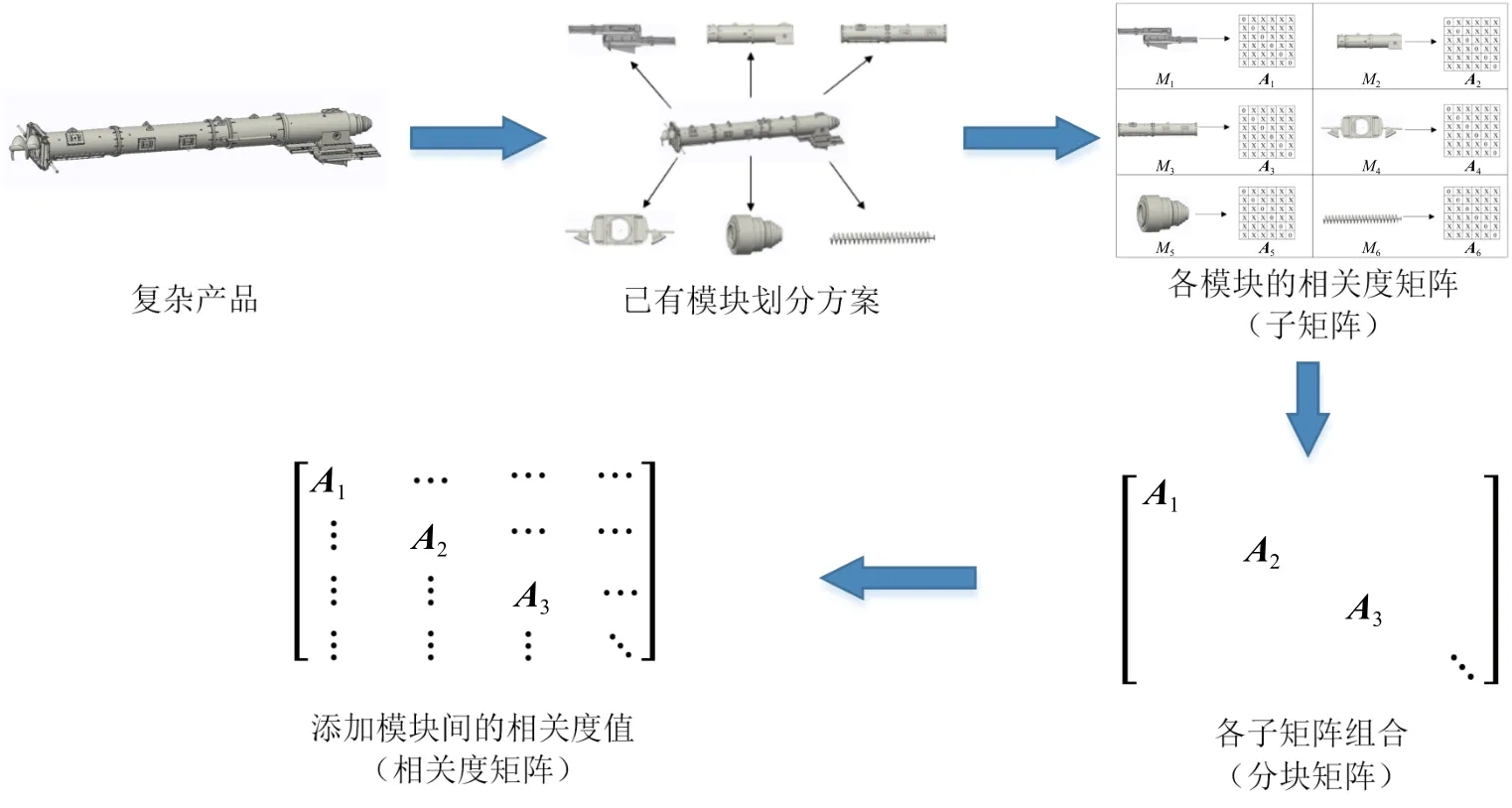
圖2 復(fù)雜產(chǎn)品相關(guān)度矩陣的建立過程Fig.2 Establishment process of complex product correlation matrix

復(fù)雜產(chǎn)品零件間的相關(guān)度取值見表1。這里考慮的是零部件之間的連接關(guān)系。

表1 復(fù)雜產(chǎn)品零件間的相關(guān)度取值Table 1 Value of correlation between parts of complex product

2 基于層次聚類的模塊劃分方案的生成

2.1 層次聚類數(shù)據(jù)的準(zhǔn)備

凝聚層次聚類（agglomerative hierarchical clustering，AHC）是一種自下向上聚合數(shù)據(jù)的聚類算法。根據(jù)算得的每一種類別的數(shù)據(jù)點(diǎn)與所有數(shù)據(jù)點(diǎn)之間的距離來確定它們之間的相似度，距離越小，則相似度越高。將最為相似的2個數(shù)據(jù)點(diǎn)進(jìn)行組合，成為一個新的數(shù)據(jù)點(diǎn)，并替換掉原來的那2個數(shù)據(jù)點(diǎn)，再進(jìn)行下次聚合。

得到相關(guān)度矩陣后，須對相關(guān)度矩陣進(jìn)行處理。

首先，將相關(guān)度矩陣A轉(zhuǎn)換為距離矩陣D。相關(guān)度值越大，兩零件間的關(guān)系越密切；而對于距離來說，兩零件間的距離越小，則其關(guān)系越密切。距離矩陣D為：

式中：B為元素全為1的矩陣。

其次，對矩陣D進(jìn)行標(biāo)準(zhǔn)化處理得到矩陣D'。D'中的元素利用式（2）進(jìn)行計(jì)算。

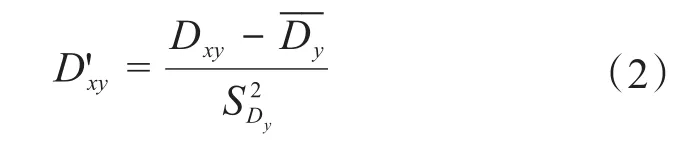
式中：Dxy、D'xy分別為矩陣D和D'第x行、第y列的元素；為矩陣D第y列數(shù)值的平均值；為矩陣D第y列數(shù)值的方差。

最后，通過矩陣D'計(jì)算距離，得到層次聚類所需要的向量T。設(shè)duw為向量u（矩陣D'的第u行）和向量w（矩陣D'的第w行）的距離，則：

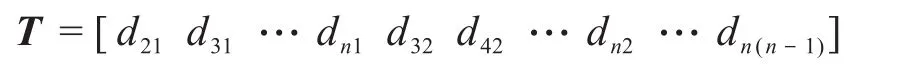
計(jì)算距離時可以采用歐幾里德距離、馬哈拉諾比斯距離、曼哈頓距離、相關(guān)距離和夾角余弦距離等，這里采用相關(guān)距離進(jìn)行計(jì)算，即：

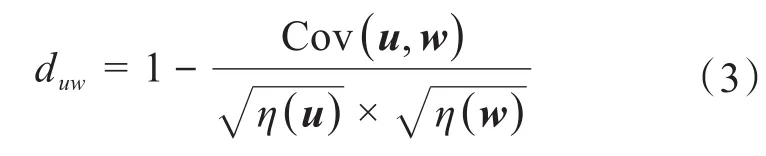
式中：Cov(u，w)為向量u和向量w的協(xié)方差；η(u)、η(w)分別為向量u、w的方差。

得到向量T后，利用MATLAB的linkage函數(shù)進(jìn)行聚類。聚類時采用平均距離（average）進(jìn)行計(jì)算。

2.2 模塊劃分結(jié)果的表示

利用層次聚類劃分模塊后，可得到不同的模塊劃分方案。則具有n個零件，被劃分為m個模塊的產(chǎn)品可表示為：{M1，M2，…，Mm}。其中，Mj={Vi}(i=1，2，…n；j=1，2，…，m)。

對于每個模塊劃分方案，存在以下條件：

1）Mj≠?，表示每個模塊內(nèi)必須有零件；

2）Mj1∩Mj2=?(j1≠j2)，表示2個模塊中不會出現(xiàn)同一零件，即一個零件只屬于一個模塊；

3 模塊劃分方案評價指標(biāo)的建立和計(jì)算

3.1 模塊度

模塊度是衡量模塊劃分效果的指標(biāo)之一，最早由Newman提出[20]。模塊度越大，表明模塊劃分效果越好。模塊度Q的計(jì)算公式如式（4）所示。Q值范圍為[-0.5，1），當(dāng)Q=0.3～0.7時，說明聚類效果較好。

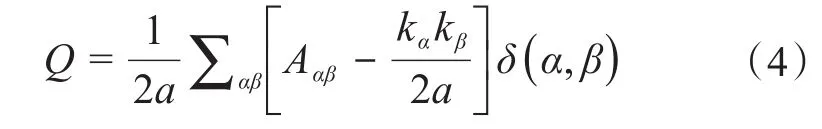
式中：2a為網(wǎng)絡(luò)中所有頂點(diǎn)的度（即與該頂點(diǎn)相連的邊的總數(shù)，若邊帶權(quán)重，則為權(quán)重之和，；α和β為其中的2個頂點(diǎn)；Aαβ為頂點(diǎn)α與頂點(diǎn)β的相關(guān)度；kα、kβ分別為頂點(diǎn)α、β的度；δ(α，β)表示α與β是否在同一個模塊，如果α與β在同一個模塊，則此值為1，否則為0。

3.2 最小描述長度

最小描述長度由Rissanen提出[21]，最初應(yīng)用于編碼。最小描述長度L的計(jì)算公式如式（5）所示。其包含2項(xiàng)，第1項(xiàng)為模塊之間運(yùn)動的熵，第2項(xiàng)為模塊內(nèi)運(yùn)動的熵（其中退出模塊也被視為運(yùn)動）。每一項(xiàng)都是根據(jù)它在特定分區(qū)中出現(xiàn)的頻率來加權(quán)的。

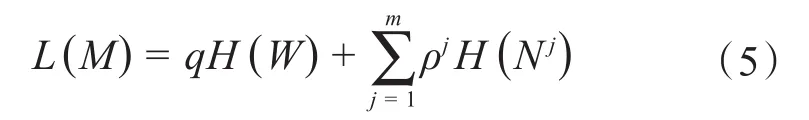
式中：q為隨機(jī)游走在任何給定步驟中切換模塊的概率；H(W)為模塊編碼的熵；H(Nj)為模塊內(nèi)部運(yùn)動的熵，包括模塊j的退出編碼；權(quán)重ρj為模塊j中發(fā)生的模塊內(nèi)運(yùn)動的概率和退出模塊j的概率。

3.3 均衡度

1）成本均衡度。

從成本的角度考慮，產(chǎn)品實(shí)際的生產(chǎn)和裝配成本與每個模塊的成本有很大的關(guān)系。在模塊劃分過程中應(yīng)盡量使模塊的成本均衡，這樣能夠降低維修和更換零部件的成本，因此提出了成本均衡度。

成本均衡度的計(jì)算過程如下：首先根據(jù)模塊劃分方案計(jì)算每個模塊的成本（即該模塊中所有零件的成本。對于結(jié)構(gòu)類零件，可用單位質(zhì)量的價格乘以零件質(zhì)量；對于密封類零件，可用單位長度的價格乘以零件長度；對于外購件，則為直接購買的價格）。得到各模塊的成本之后，根據(jù)式（6）計(jì)算成本的信息熵：

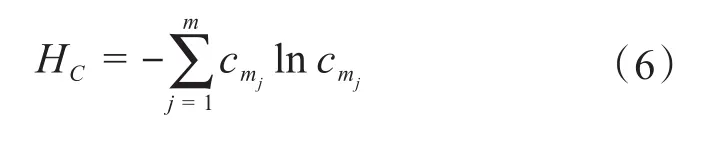
式中：HC為產(chǎn)品成本的信息熵；cmj為模塊j的相對成本，為模塊j的成本。

成本的信息熵值反映了模塊劃分的多少及各模塊成本分布的均勻程度：模塊劃分越多，各模塊的成本相差越小，熵值就越大。但在不同的模塊劃分方案下，當(dāng)模塊數(shù)不同時，信息熵值缺乏可比性[22]。因此，基于該信息熵函數(shù)引入模塊劃分的成本均衡度公式，在理論上當(dāng)各模塊的成本相等時，信息熵取得最大值HCmax=lnm。因此成本均衡度JC為：

JC取值為0～1，JC值越大，表明各模塊的成本越均衡。

2）復(fù)雜度均衡度。

制造和裝配模塊的工作量即為模塊的復(fù)雜度。在復(fù)雜產(chǎn)品的模塊劃分中，應(yīng)盡量使模塊的復(fù)雜度均衡。復(fù)雜度的計(jì)算公式如式（8）所示，其包含2項(xiàng)：第1項(xiàng)為模塊內(nèi)每個零件的復(fù)雜度，與模塊制造時的工作量相關(guān)聯(lián)；第2項(xiàng)為模塊內(nèi)各零件由于連接關(guān)系產(chǎn)生的額外復(fù)雜度，與模塊裝配時的工作量相關(guān)聯(lián)。

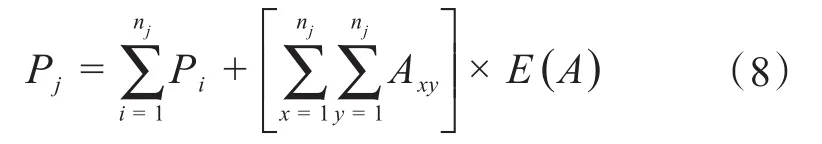
式中：Pj為模塊j的復(fù)雜度；nj為模塊j中零件的個數(shù)；Axy為矩陣A中第x行、第y列的元素λb為相關(guān)度矩陣A的第b個特征值。

與成本均衡度類似，得到每個模塊的復(fù)雜度后，再通過式（9）計(jì)算復(fù)雜度信息熵：

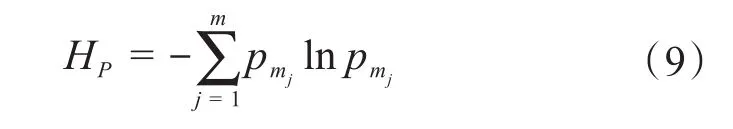
式中：HP為產(chǎn)品復(fù)雜度的信息熵；pmj為模塊j的相對復(fù)雜性為模塊j的復(fù)雜度。

同理，在不同模塊劃分方案下，當(dāng)模塊數(shù)不同時，信息熵值缺乏可比性。因此，基于該信息熵函數(shù)引入模塊劃分的復(fù)雜度均衡度公式，在理論上當(dāng)各模塊的復(fù)雜度相等時，信息熵取得最大值HPmax=lnm。因此復(fù)雜度均衡度為：

JP取值為0～1，JP值越大，表明各模塊的復(fù)雜度越均衡。

3.4 評價指標(biāo)的計(jì)算

在計(jì)算模塊度和均衡度時，須利用X矩陣表示模塊劃分方案。每一種劃分方案對應(yīng)一個X矩陣，X矩陣中的元素只為0或1。

計(jì)算完各個指標(biāo)后，最終的綜合評價指標(biāo)I為：

式中：f為評價指標(biāo)個數(shù)；ωt為第t個評價指標(biāo)的權(quán)重值；It為第t個評價指標(biāo)。

模塊度和均衡度的計(jì)算過程如圖3所示。

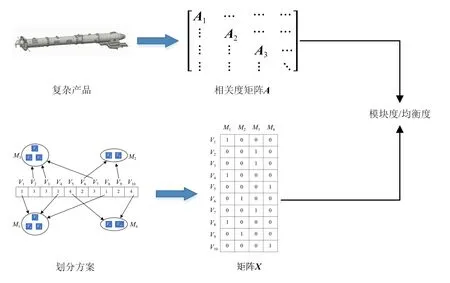
圖3 模塊度和均衡度的計(jì)算過程Fig.3 Calculation process of modularity and equilibrium

4 基于熵權(quán)法的評價指標(biāo)權(quán)重的計(jì)算

利用熵權(quán)法確定模塊劃分方案評價指標(biāo)的權(quán)重，步驟如下：

1）建立模塊劃分指標(biāo)矩陣S，若有g(shù)個劃分方案、f個評價指標(biāo)，則S為g×f階矩陣，srt為第r個劃分方案的第t個指標(biāo)值 (r=1，2，…，g；t=1，2，…，f)，S=(srt)g×f。

2）對數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理，將指標(biāo)絕對值轉(zhuǎn)化為相對值zrt，正向指標(biāo)zrt+和負(fù)向指標(biāo)zrt-如式（12）所示：

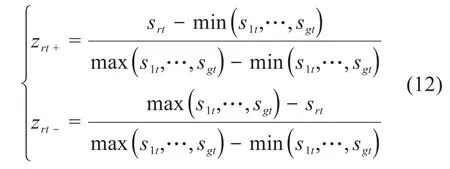
3）根據(jù)式（13）計(jì)算劃分方案中各指標(biāo)所占的比重εrt，然后根據(jù)式（14）計(jì)算各個指標(biāo)的信息熵值et。

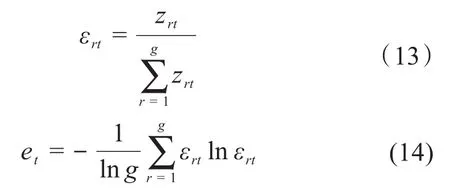
4）根據(jù)式（15）計(jì)算出劃分方案中各項(xiàng)指標(biāo)的客觀權(quán)重值ωr。

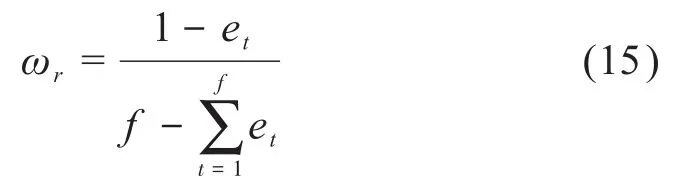
5 案例分析

以盾構(gòu)螺旋輸送機(jī)為例來驗(yàn)證所提出的復(fù)雜產(chǎn)品架構(gòu)評價方法的正確性。螺旋輸送機(jī)是土壓平衡盾構(gòu)機(jī)排土和建立土壓平衡的主要設(shè)備，其結(jié)構(gòu)如圖4所示。螺旋輸送機(jī)工作時，深入土艙內(nèi)的螺桿和螺旋葉片在液壓馬達(dá)的驅(qū)動下旋轉(zhuǎn)，土艙內(nèi)的土碴隨著螺旋軸的旋轉(zhuǎn)而上升，然后經(jīng)出碴門排出[23]。螺旋輸送機(jī)的零件數(shù)眾多，集成度高，研發(fā)成本高，屬典型的復(fù)雜產(chǎn)品。因此，模塊劃分對其設(shè)計(jì)、制造、裝配和維修具有重要意義。

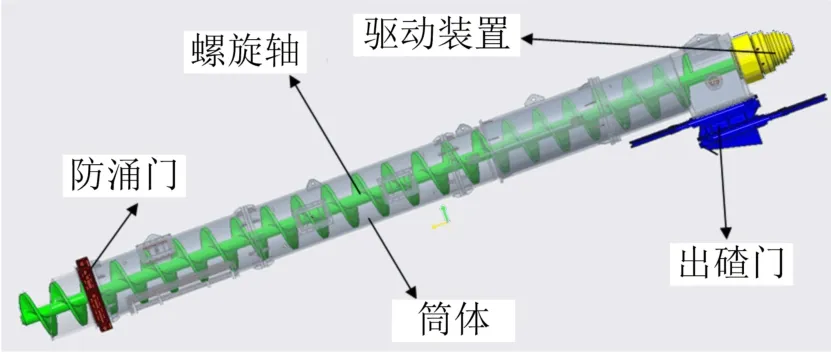
圖4 盾構(gòu)螺旋輸送機(jī)的結(jié)構(gòu)Fig.4 Structure of shield screw conveyor

5.1 盾構(gòu)螺旋輸送機(jī)相關(guān)度矩陣的建立

盾構(gòu)螺旋輸送機(jī)已有的模塊劃分方案如表2和圖5所示，共分為出碴門、伸縮節(jié)、連接節(jié)、防涌門、驅(qū)動裝置和螺旋軸六個模塊。

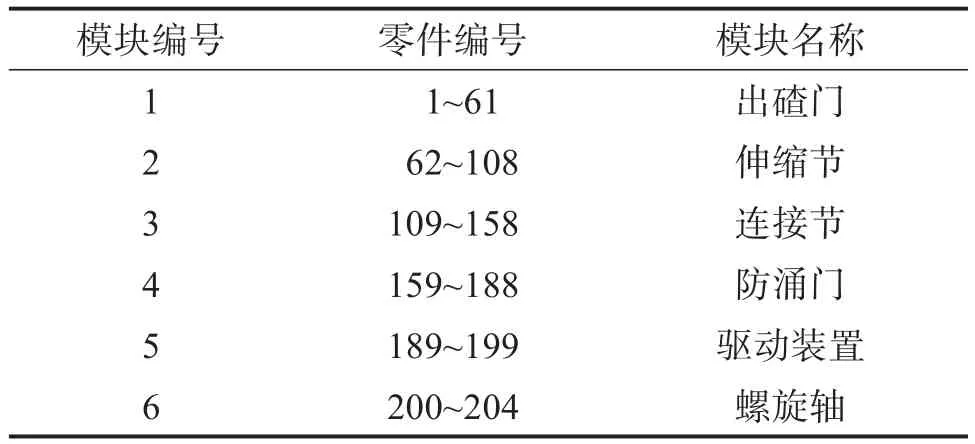
表2 盾構(gòu)螺旋輸送機(jī)已有模塊劃分方案Table 2 Existing module division scheme of shield screw conveyor

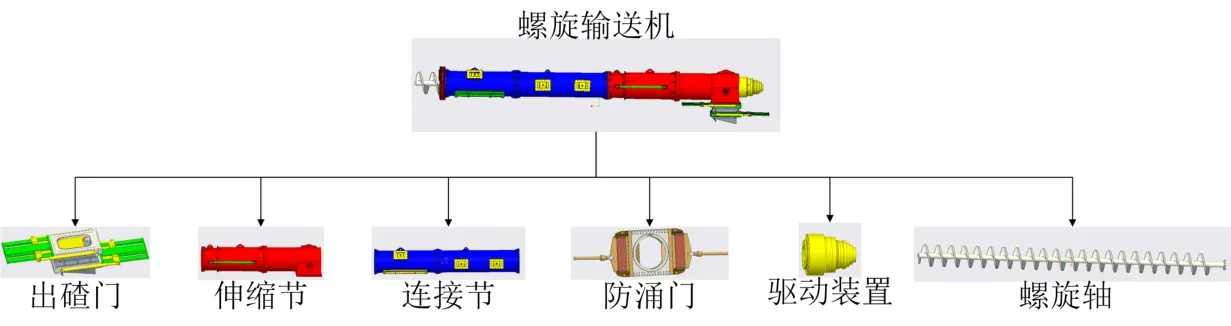
圖5 盾構(gòu)螺旋輸送機(jī)已劃分的模塊Fig.5 Existing division modules of shield screw conveyor

利用這6個模塊構(gòu)造螺旋輸送機(jī)的相關(guān)度矩陣。首先建立每個模塊的相關(guān)度矩陣A1、A2、A3、A4、A5和A6，其網(wǎng)絡(luò)圖如圖6所示。圖中頂點(diǎn)以“零件編號-成本-復(fù)雜度”示出，其中：零件成本通過表3算得；零件復(fù)雜度根據(jù)零件制造時的難易程度進(jìn)行量化而得出，如表4所示。

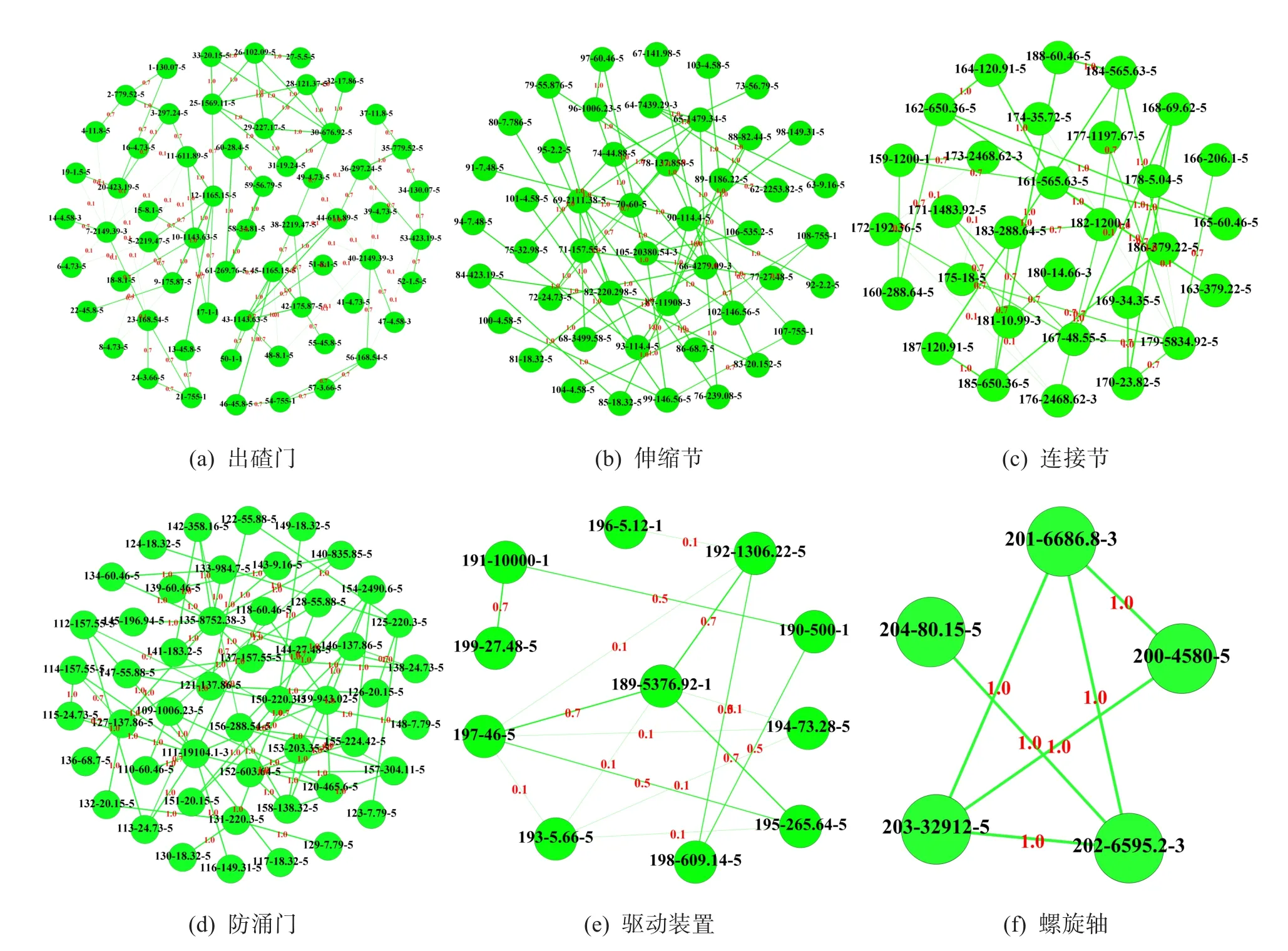
圖6 盾構(gòu)螺旋輸送機(jī)已有劃分模塊的網(wǎng)絡(luò)圖Fig.6 Network diagram of existing division modules of shield screw conveyor

表3 盾構(gòu)螺旋輸送機(jī)的零件成本Table 3 Parts cost of shield screw conveyor

表4 盾構(gòu)螺旋輸送機(jī)的零件復(fù)雜度Table 4 Part complexity of shield screw conveyor

6個模塊的相關(guān)度矩陣建立后，再添加模塊間的相關(guān)度。這6個模塊間的連接均為螺栓連接，相關(guān)度為0.7。其連接關(guān)系如圖7所示。在相關(guān)度矩陣中的對應(yīng)位置添加模塊間的相關(guān)度數(shù)值后，即得到盾構(gòu)螺旋輸送機(jī)整體的相關(guān)度矩陣A，其整體網(wǎng)絡(luò)關(guān)系如圖8所示。

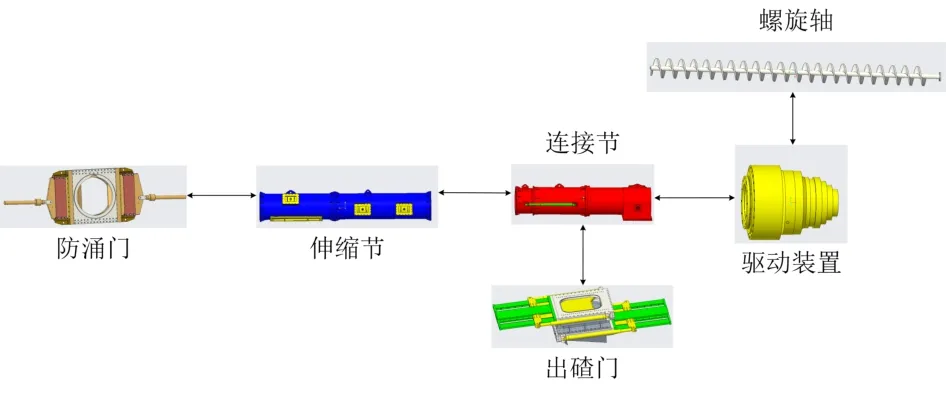
圖7 盾構(gòu)螺旋輸送機(jī)6個模塊間的連接關(guān)系示意Fig.7 Schematic of connection relationship between six modules of shield screw conveyor

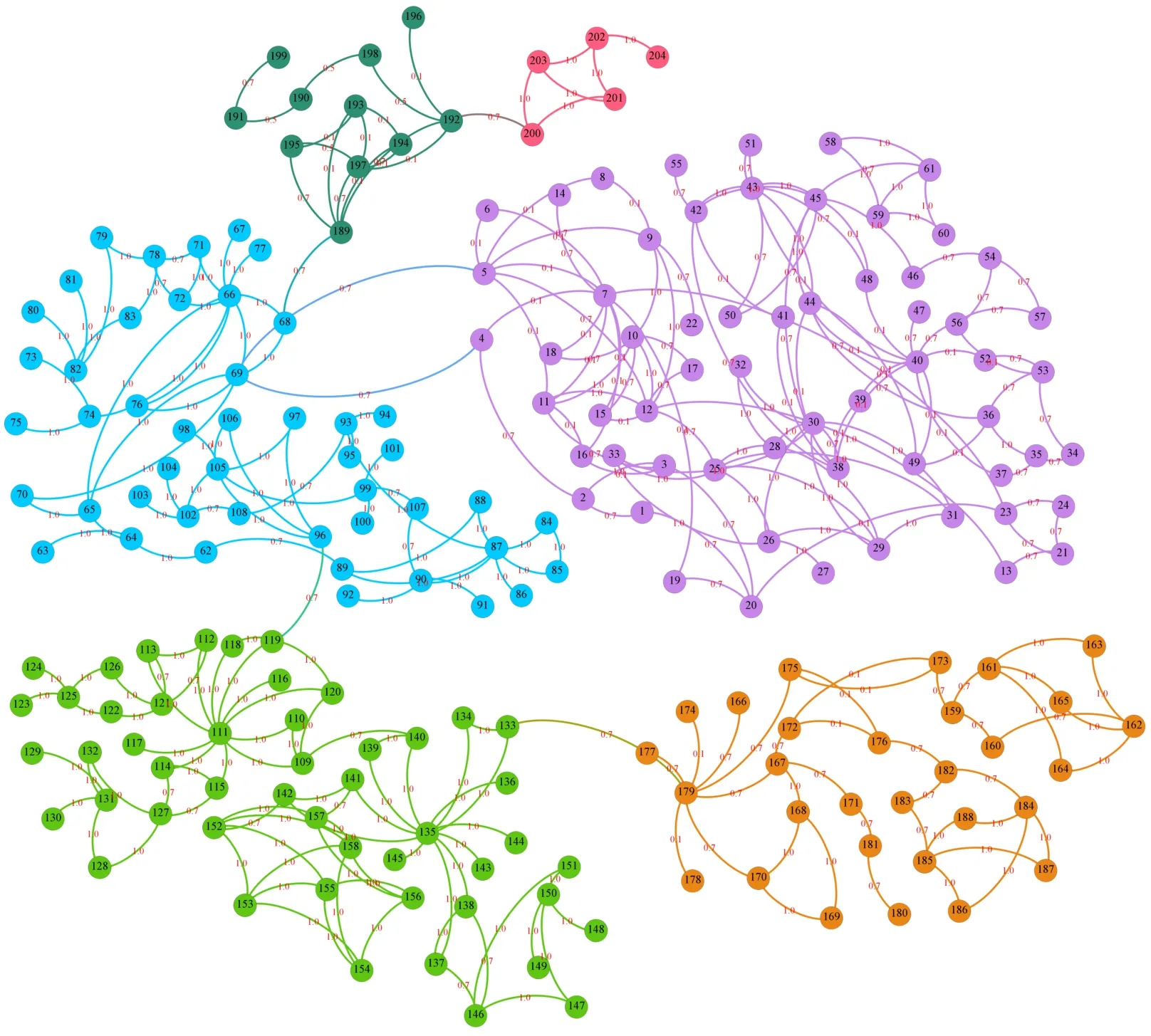
圖8 盾構(gòu)螺旋輸送機(jī)整體網(wǎng)絡(luò)圖Fig.8 Overall network diagram of shield screw conveyor

5.2 盾構(gòu)螺旋輸送機(jī)的模塊劃分

利用層次聚類進(jìn)行模塊劃分。不同的聚類數(shù)形成不同的模塊劃分方案。一般地，產(chǎn)品的模塊數(shù)不會超過零件數(shù)的算數(shù)平方根。螺旋輸送機(jī)共有204個零件，因此取最大模塊數(shù)為15(> 204≈14.28)，得到如表5所示的模塊劃分方案。

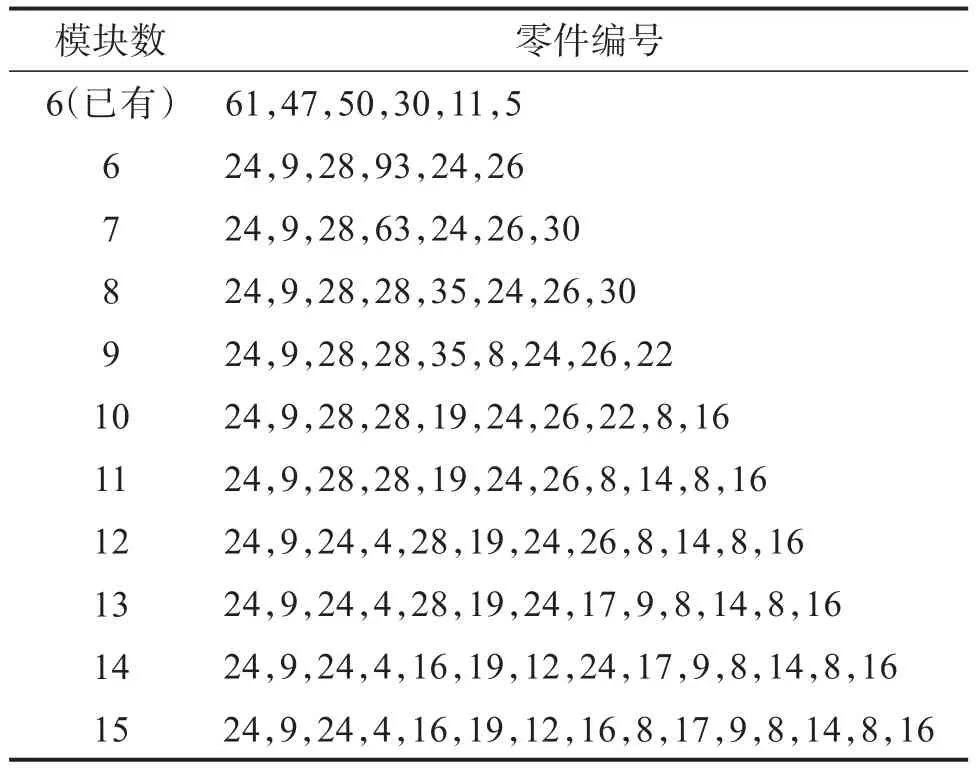
表5 盾構(gòu)螺旋輸送機(jī)模塊劃分方案Table 5 Module division scheme of shield screw conveyor

5.3 盾構(gòu)螺旋輸送機(jī)模塊劃分方案的評價

計(jì)算盾構(gòu)螺旋輸送機(jī)模塊劃分方案的評價指標(biāo)，結(jié)果如表6和圖9所示。最小描述長度值越小，其他三項(xiàng)指標(biāo)值越大，則模塊劃分效果越好，制造和裝配效率越高。最小描述長度取值范圍不在0～1之間，因此對其取倒數(shù)并作歸一化處理，得到-L。

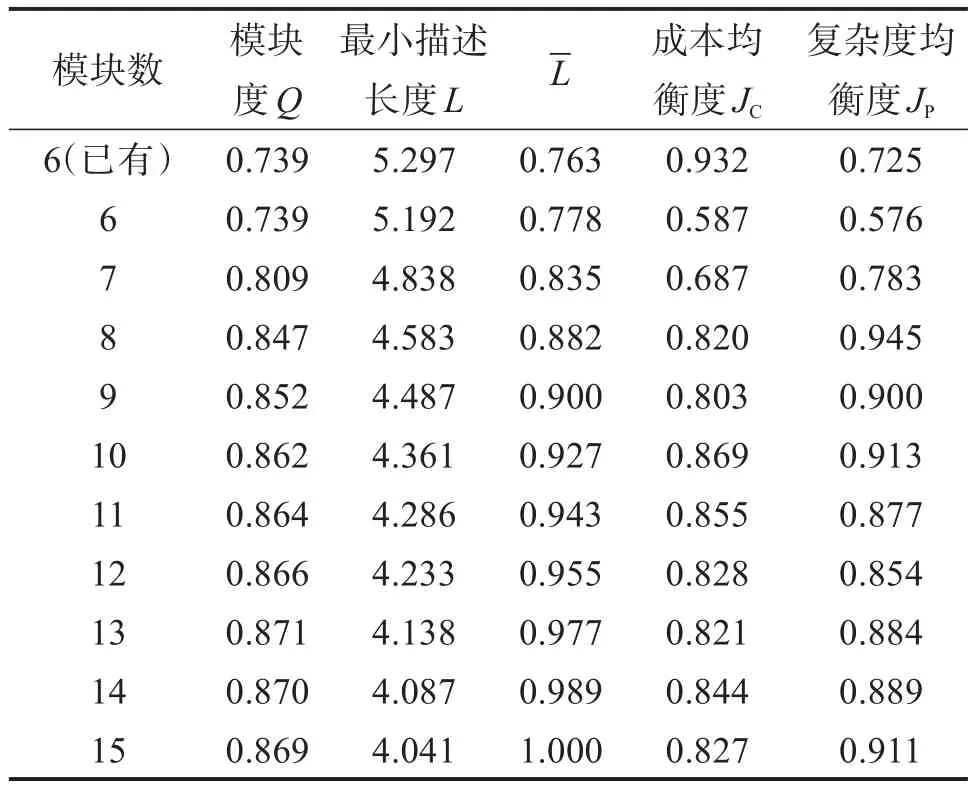
表6 盾構(gòu)螺旋輸送機(jī)模塊劃分方案的評價指標(biāo)值Table 6 Evaluation index value of module division scheme of shield screw conveyor

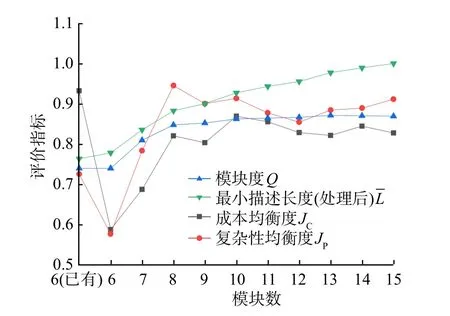
圖9 盾構(gòu)螺旋輸送機(jī)模塊劃分方案評價指標(biāo)的變化曲線Fig.9 Changing curves of evaluation indexes under different module division schemes of shield screw conveyor

由圖9可知，模塊度與最小描述長度（處理后）的變化趨勢類似，成本均衡度與復(fù)雜度均衡度的變化趨勢類似。經(jīng)過計(jì)算可得，模塊度和最小描述長度（處理后）的相關(guān)系數(shù)為0.94，成本均衡度和復(fù)雜度均衡度的相關(guān)系數(shù)為0.62。

成本均衡度與復(fù)雜度均衡度的相關(guān)系數(shù)比模塊度與最小描述長度（處理后）的相關(guān)系數(shù)小，因此，在選擇綜合評價指標(biāo)時，在模塊度和最小描述長度中選擇一個，成本均衡度、復(fù)雜度均衡度則都須考慮。

1）考慮模塊度、成本均衡度和復(fù)雜度均衡度時，利用熵權(quán)法確定其權(quán)重值為：

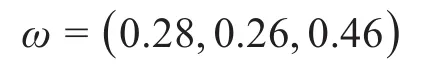
此時各評價指標(biāo)值和綜合評價指標(biāo)值如表7所示。

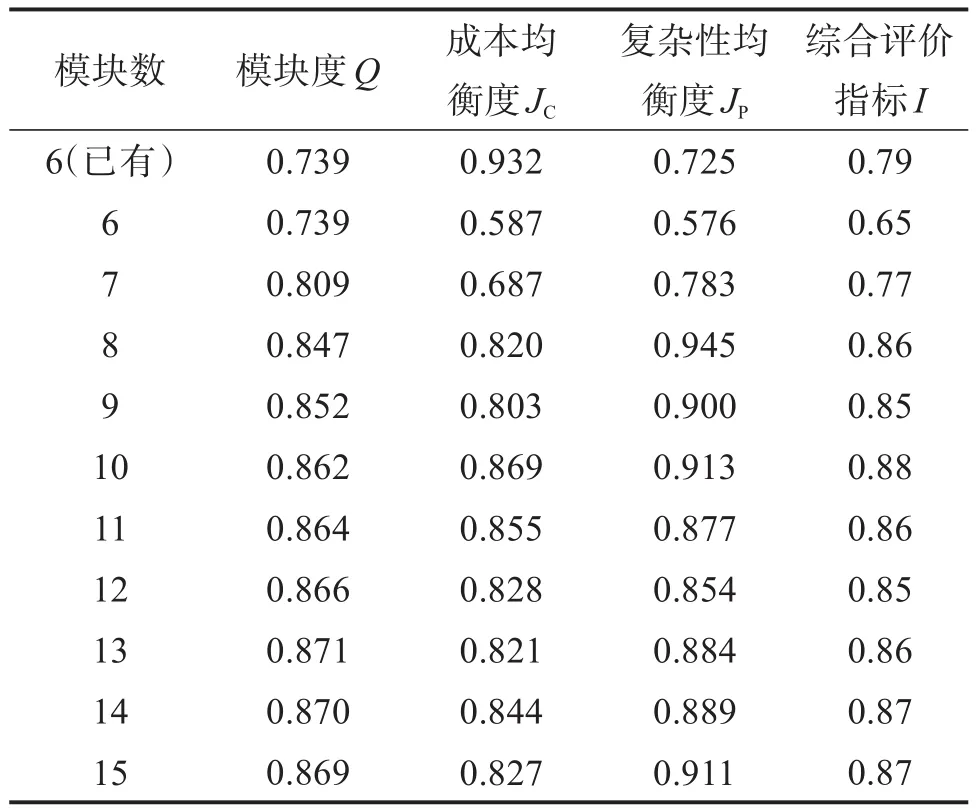
表7 考慮模塊度和均衡度時的評價指標(biāo)值Table 7 Evaluation index value when considering modularity and equilibrium

2）考慮最小描述長度、成本均衡度和復(fù)雜度均衡度時，利用熵權(quán)法確定其權(quán)重值為：

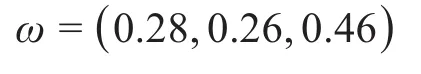
此時各評價指標(biāo)值和綜合評價指標(biāo)值如表8所示。

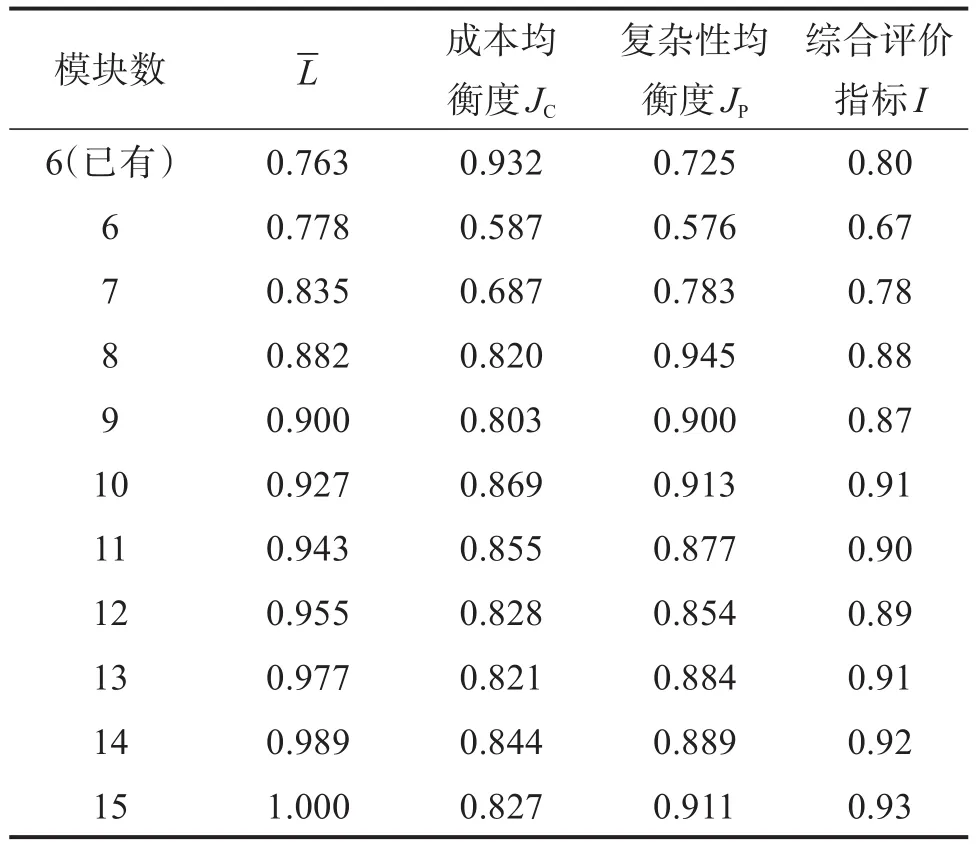
表8 考慮最小描述長度和均衡度時的評價指標(biāo)值Table 8 Evaluation index value when considering minimum description length and equilibrium

5.4 模塊劃分方案的改進(jìn)

2種評價方案下綜合評價指標(biāo)的變化曲線如圖10所示。考慮模塊度和均衡度時綜合評價指標(biāo)的最大值為0.88，此時模塊數(shù)為10。考慮最小描述長度和均衡度時綜合評價指標(biāo)的最大值為0.93，此時模塊數(shù)為15。

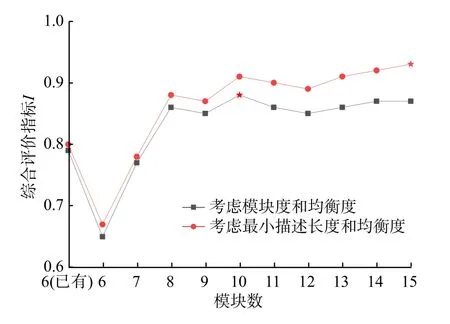
圖10 2種評價方案下綜合評價指標(biāo)的變化曲線Fig.10 Changing curves of comprehensive evaluation index under two evaluation schemes

考慮模塊度和均衡度時的最優(yōu)模塊劃分方案如表9所示，考慮最小描述長度和均衡度時的最優(yōu)模塊劃分方案如表10所示。當(dāng)模塊數(shù)為15時，伸縮部分分成了兩部分（模塊6和模塊7）；將中間節(jié)的一個檢修門單獨(dú)分成了一個模塊（模塊9）；將固定節(jié)的蓋板單獨(dú)分成了一個模塊（模塊11）；將防涌門分成了左門板、面板、右門板三部分，如圖11所示。由于這些部分存在結(jié)構(gòu)和功能上的聯(lián)系，將其拆開并不合理，因此模塊數(shù)為10的劃分方案較為合理，且其綜合評價指標(biāo)也較好。由于該方案也將防涌門的右門板單獨(dú)作為一個模塊，因此改進(jìn)方案，將防涌門作為一個模塊看待，則為9個模塊，如表11所示。

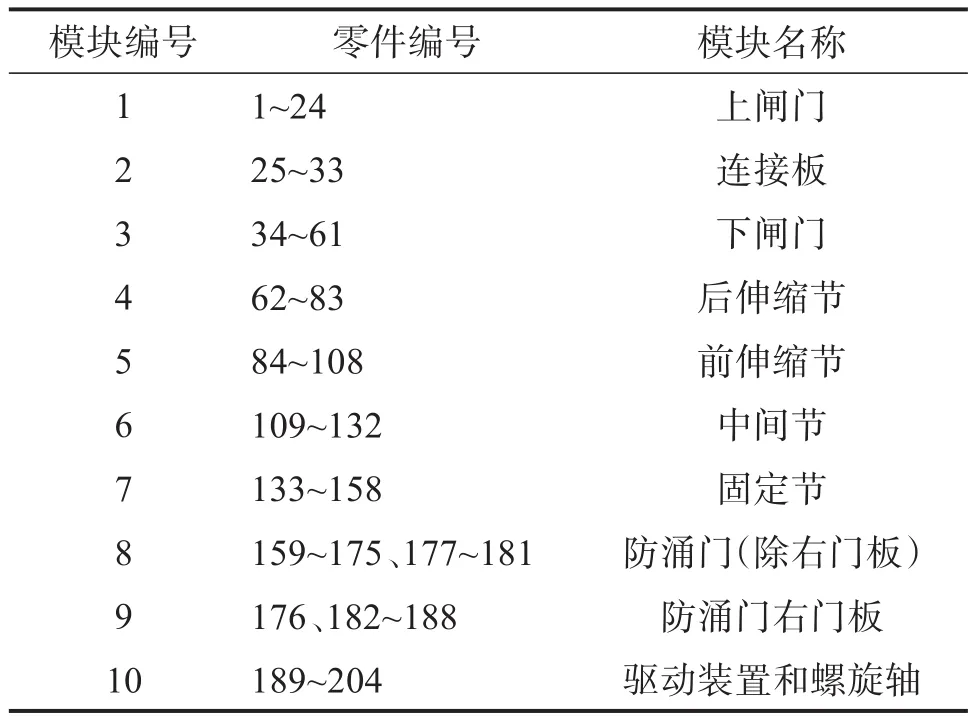
表9 考慮模塊度和均衡度時的最優(yōu)模塊劃分方案Table 9 Optimal module division scheme when considering modularity and equilibrium

表10 考慮最小描述長度和均衡度時的最優(yōu)模塊劃分方案Table 10 Optimal module division scheme when considering minimum description length and equilibrium

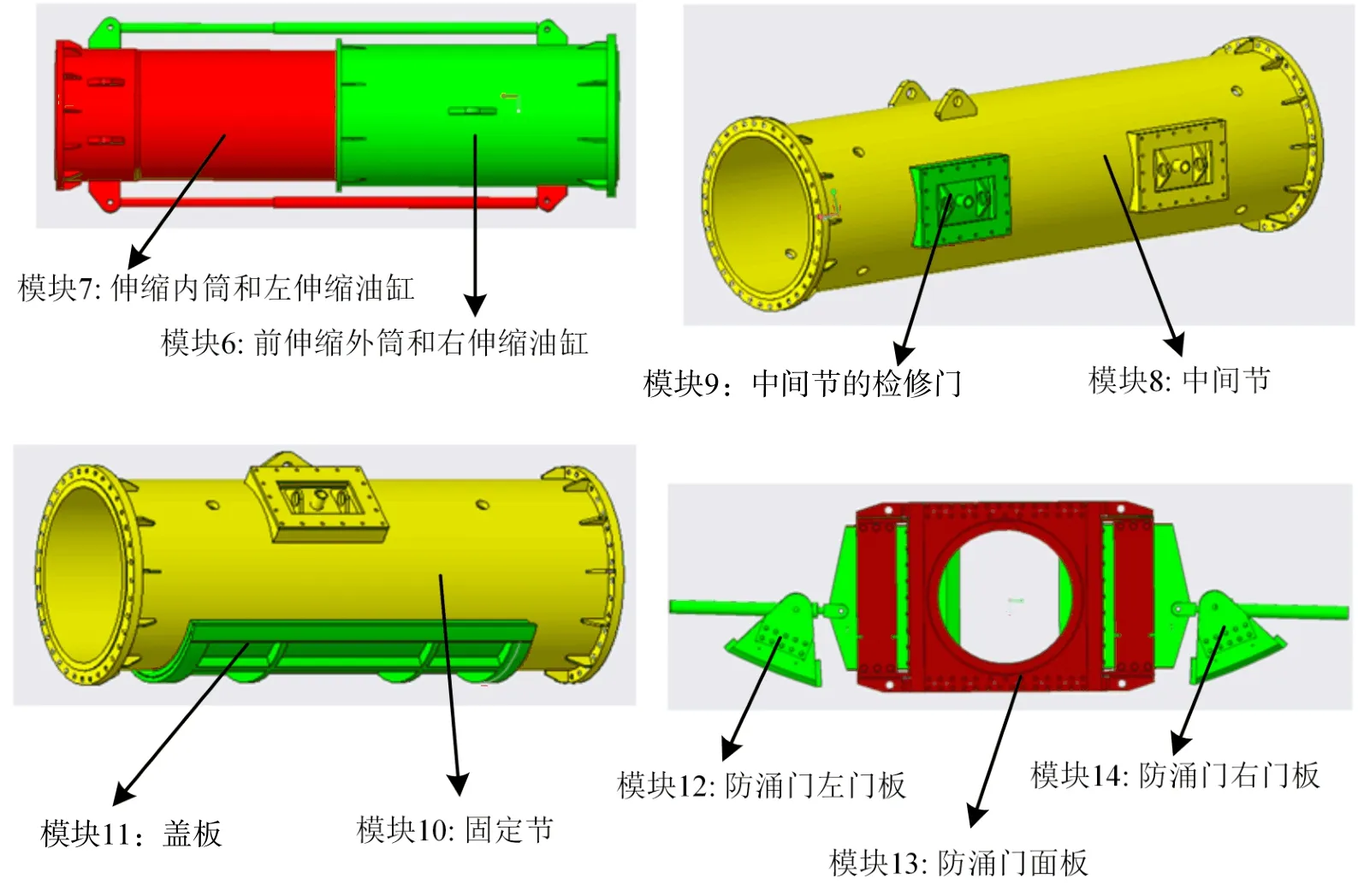
圖11 考慮最小描述長度和均衡度時最優(yōu)模塊劃分方案中的模塊6至模塊14Fig.11 Module 6 to module 14 in the optimal module division scheme when considering minimum description length and equilibrium

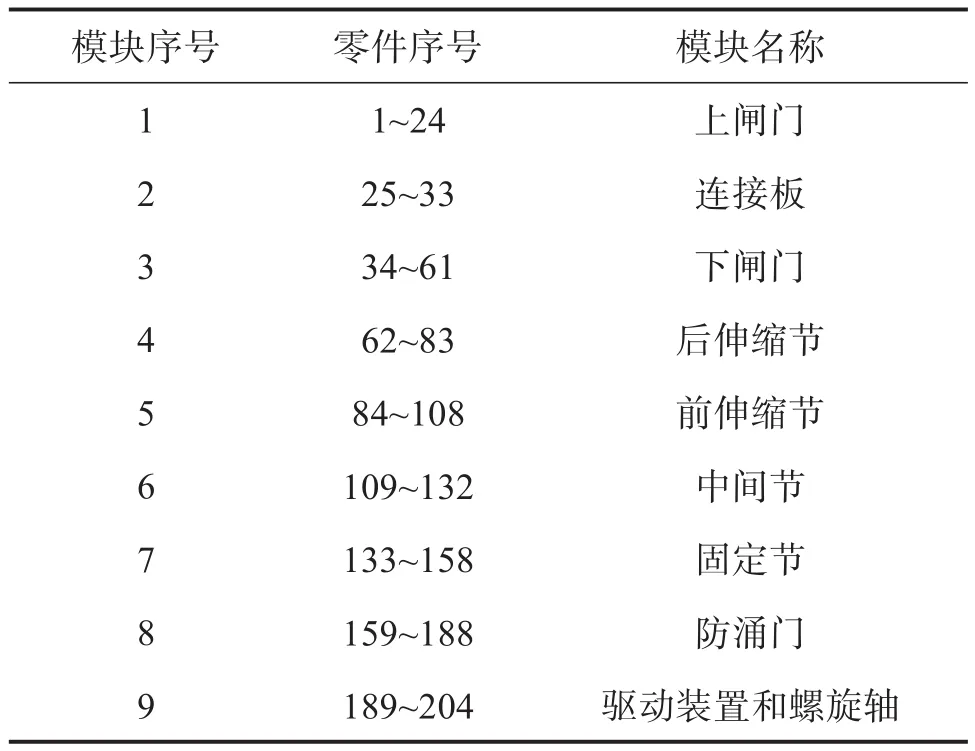
表11 改進(jìn)后的模塊劃分方案Table 11 Improved module division scheme

根據(jù)改進(jìn)后的模塊劃分方案計(jì)算模塊度和均衡度。雖然模塊度由0.862降低到0.855，但是均衡度由1.782提高到1.801，綜合評價指標(biāo)由0.877提高到0.880。不管從評價指標(biāo)數(shù)值還是從實(shí)際劃分結(jié)果來看，改進(jìn)后的模塊劃分方案比較合理。方案改進(jìn)后盾構(gòu)螺旋輸送機(jī)的產(chǎn)品架構(gòu)如圖12所示。

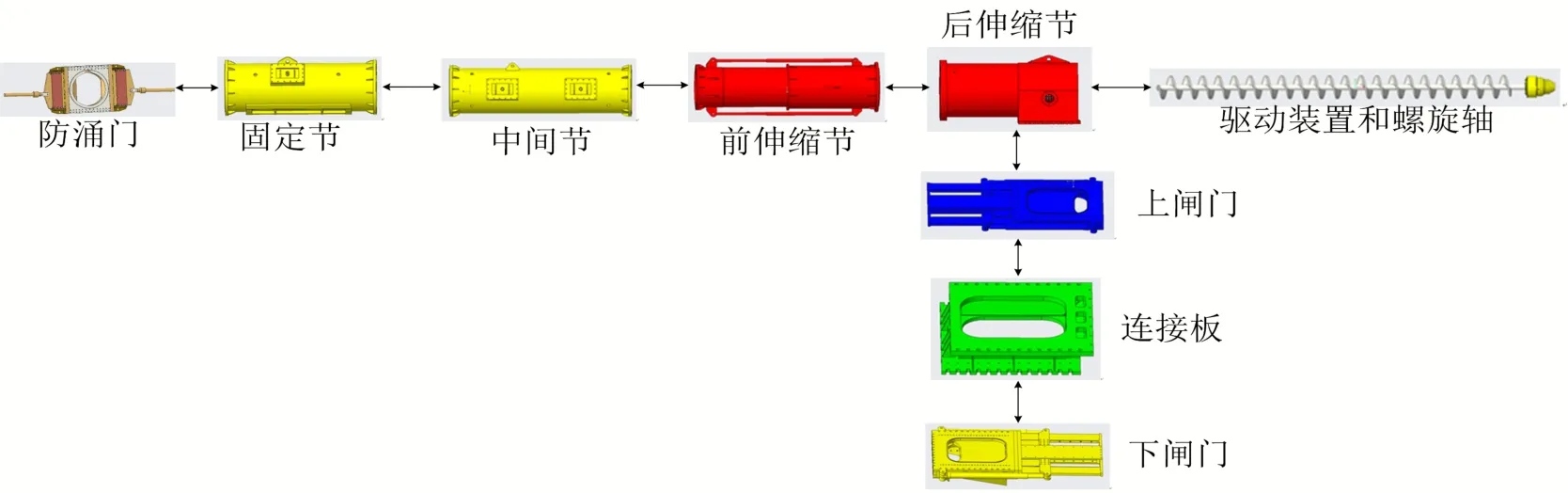
圖12 方案改進(jìn)后盾構(gòu)螺旋輸送機(jī)的產(chǎn)品架構(gòu)Fig.12 Product architecture of shield screw conveyor after scheme improvement

6 結(jié) 論

1）提出了復(fù)雜產(chǎn)品架構(gòu)評價方法和評價指標(biāo)，給出了評價指標(biāo)的計(jì)算公式。結(jié)合模塊度、最小描述長度建立的復(fù)雜產(chǎn)品架構(gòu)綜合評價方法可以解決復(fù)雜產(chǎn)品模塊劃分方案單目標(biāo)評價時成本與復(fù)雜度不均衡的問題，提高了零部件的制造和裝配效率。

2）以盾構(gòu)螺旋輸送機(jī)為例，對提出的綜合評價方法進(jìn)行了驗(yàn)證，完成了復(fù)雜產(chǎn)品架構(gòu)的評價與改進(jìn)。結(jié)果表明，基于模塊度和均衡度的綜合評價方法比單目標(biāo)評價方法合理，可以得到更合理的盾構(gòu)螺旋輸送機(jī)產(chǎn)品架構(gòu)。