基于SSD的碼垛機械臂關節速度糾偏運動規劃

王清清，奚 琳

(1.安徽信息工程學院機械工程學院，安徽蕪湖 241000；2.安徽工程大學機械工程學院，安徽蕪湖 241000)

1 引言

隨著全球經濟的蓬勃發展，人們對產品的精度要求也越來越高，加上人工成本的不斷提升，機器人加工已成為大中型企業首選的加工方式[1-3]。隨著機器人的逐漸興起，碼垛成為包裝過程中必不可少的流程，是物流自動化技術的新興技術。碼垛作業在現企業物流管理中占據十分重要的地位。早在80年代初期，一些工業發達的國家已經在自動化、機械化碼垛方面取得了較好的發展，實現自動化碼垛能夠提升物流速度，保障員工安全，減少物料浪費[4]。為了確保碼垛機械臂保質保量完成工作任務，機械臂需要根據一定運動軌跡進行操作，軌跡規劃是碼垛機械臂完成任務和運行性能的基礎[5]。為此相關研究人員進行了很多研究，并取得了一定成果。

余亮等人[6]提出研究局部閉鏈碼垛機器人運動學分析及軌跡規劃方法。該方法利用D-H法獲取局部閉鏈碼垛機器人運動學正逆解，根據任務需要，通過可達工作空間完成碼垛機器人路徑規劃，采取將規劃結果與運動學逆解相結合的方式，確定機器人各關節位移和速度之間的時變關系，達到縮短運行周期，提升工作效率，但該方法針對碼垛機械臂關節速度糾偏存在的影響因素分析甚少，存在一定局限性。張玲[7]提出基于三次樣條曲線的碼垛機器人平滑軌跡規劃方法。針對碼垛機器人運行軌跡，采用三次樣條曲線進行規劃，將軌跡曲線的參數連續性進行結合，實現碼垛機器人平滑運行軌跡，保證其工作過程中的運動平穩性和連續性。該方法可有效控制碼垛機器人的穩定運行，但該方法在遇到障礙物時壁障性能較差。

基于此，本文提出基于SSD的碼垛機械臂關機速度糾偏運動規劃方法。借助SSD算法對研究目標進行自動識別，并通過利用直流電機PWM糾偏調速控制模型和PID糾偏控制算法有效實現速度偏差的校正。與傳統方法相比，本文方法有效提升碼垛機械臂關節運動精度和平穩性，成功實現任務的軌跡規劃。

2 碼垛機械臂關節速度糾偏運動規劃

2.1 基于SSD算法的目標識別

SSD算法通過不同比例候選框和特征圖預測目標物體，利用全卷積代替全連接層，有效提升算法精度和速度[8]。正樣本為準確與真實框相匹配的設定，負樣本為其它框設定，其位置、置信度和反向傳播三種損失的加權總和為算法的損失值，網絡結構如圖1所示。

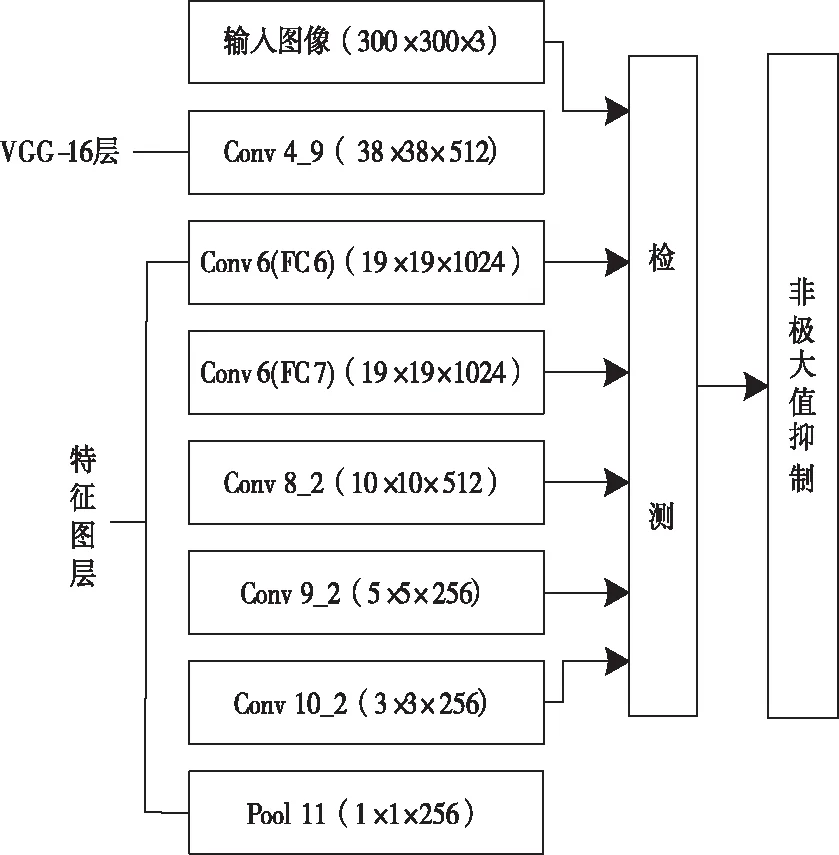
圖1 SSD網絡結構圖

以VGG 16為算法基準網絡，將該全連接層轉變成卷積層。對參數為2×2的最大池化層轉變為3×3的最大池化，池化層的轉變能夠帶動感受野發生改變，通過帶孔卷積對卷積核進行膨脹處理，使感受野同時增大，豐富卷積之后的圖像信息。

輸入分辨率為300×300的圖片，3×3的卷積核，滑動步長(水平方向和垂直方向)為1，輸出150×150×64，該輸出通過對2×2的池化層進行池化操作獲取。

匹配真實框與默認框，建立真實框與默認框的關系。設定兩框之間的閾值比默認框高，促使產生若干個重疊的默認框，便于不再只針對最大重疊默認框進行選擇，保證置信度的精準。

假設第i個默認框匹配p類別的第j個真實框，其中，大于默認框的閾值有若干個，位置損失加上置信損失為目標損失函數，即

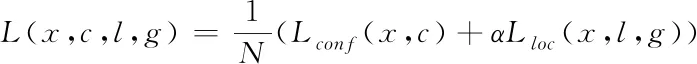
(1)

其中，默認框數量為N，位置損失為Lloc(x，l，g)，置信損失為Lconf(x，c)，α為1，位置損失表示真實框與損失框之間的損失，即

(2)

置信度損失為

(3)

SSD算法不受單尺度檢測的限制，對于邊框類別分數和位置偏移的預測是通過小卷積預測器完成，可顯著提升檢測精度。同時，在單個網絡中封鎖住所有計算，確保在保證精度的基礎上對整體實時性具有提升作用。

2.2 碼垛機械臂關節速度糾偏PID控制

2.2.1 直流電機調速控制

以SSD算法識別結果為基礎，采用PLC為控制器，針對碼垛機械臂的電機轉速和電流采用PWN調速方式進行PID控制[9]。調速模型如圖2所示。

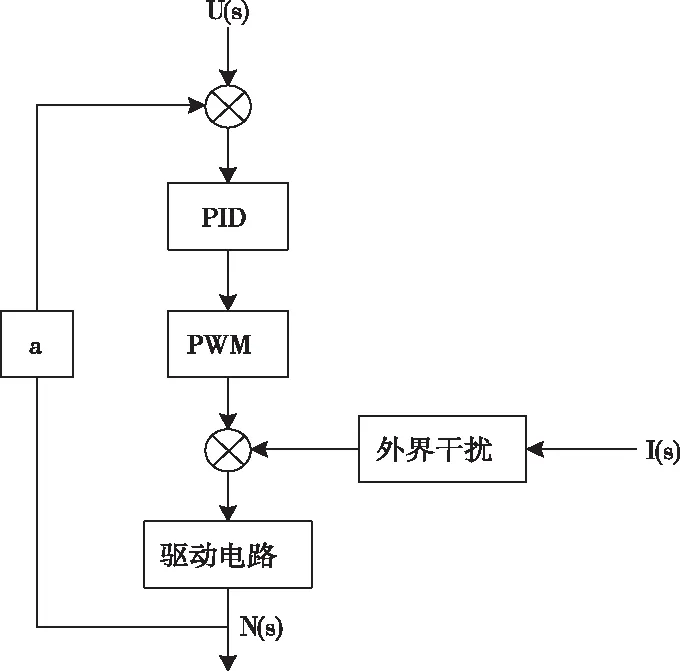
圖2 直流電機動態PWM調速模型

對于外界干擾需要進行及時處理，不然會引起輸出值變化產生誤差，無刷直流電機調速模型能夠通過PID控制實現一定程度的干擾調節，有效減少轉速因干擾而產生的影響[10]。

2.2.2 PID糾偏實現方法

采用左輪和右輪轉速偏差，用以表示碼垛機械臂的運動過程，PID糾偏控制公式為

(4)

其中，u表示驅動電壓控制電壓，e(k)表示系統偏差，ec表示系統變化變化率，Kp表示比例系數，KI表示積分系數，KD表示微分系數。

由于當前狀態決定本次輸出值，在計算過程中，疊加系統偏差進行求和，導致工作量偏大，為了減少偏大的瞬間微分值，通過監看測定值進行PID指令控制，如圖3所示。

圖3 PID指令控制框圖

PID表示公式為：

(5)

其中，u(k)表示輸出值，uPV(k)表示測定值，uSV(k)表示目標值。

在PID控制器中，輸入SV偏差和PV偏差，分別設置比例系數參數、積分系數參數和微分系數參數，對直流電機進行調速。根據測定值PV的微分狀況，測定值變化量與車輪速度變化量成正比，當測定值變化量與輸出值成反比時，利用PWM波形式對電機進行調速。

3 碼垛機械臂關節運動軌跡規劃實現

碼垛機械臂關節角利用運動學逆解的方式進行目標位姿與預定軌跡的求解，結合2.2小節的PID機械臂關節速度糾偏方式，共同完成碼垛機械臂關節運動軌跡規劃。

3.1 軌跡規劃法

利用“5-3-5”軌跡規劃法控制抓取放置過程中碼垛機械臂的速度、加速度和精度。具體步驟為：①起點→抬升點，采用五次多項式進行規劃；②抬升點→下降點，采用三次多項式進行規劃；③下降點→終點，采用采用五次多項式進行規劃。各個關節的目標軌跡多項式方程為

(6)

其中，θ1、θ2和θ3分別表示Ⅰ軸、Ⅱ軸和Ⅲ軸的關節變量，ζ表示軌跡。

完全滿足以下四個條件才能體現四線運動連續性，即：

①軌跡中任何一段初始和末端兩個位置需要與四個(A、B、C、D)關節角位置保持一致；

②軌跡第一段初始和第三段末端的角速度和角加速度相同，且為0；

③軌跡前后段之間角位置、角加速度和角加速度保持一致；

④根據關節軸的關節變量，設置軌跡ζ1f、ζ2f和ζ3f和所需時間，分別為2s、4s和2s。

3.2 軌跡規劃動力學分析

碼垛機械臂每個關節運行需要具有較大的力和力矩，保證關節速度和加速度滿足預期位置精度。利用拉格朗日構建系統動力學方程，碼垛機械臂關節速度糾偏運動力矩公式為

(7)

展開式(7)得

(8)

其中，Fii表示有效慣量，Fi表示重力，Fiji和Fijj分別表示關節i、j之間的耦合慣量和耦合力矩，表示在關節i上關節j處速度產生的向心力。

每個關節驅動力矩方程為

(9)

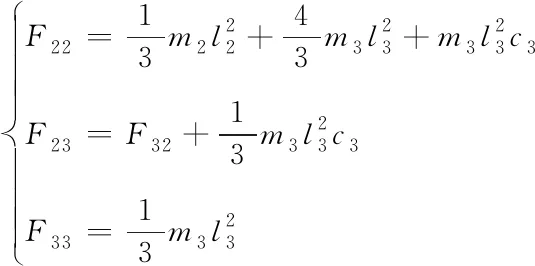
(10)

重力項為

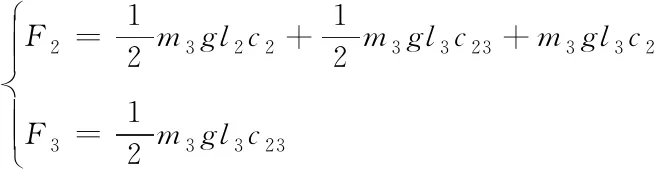
(11)

其中，m2、m3分別表示大臂小臂質量。li表示相應臂的長度。

設質心在l的中心，將慣性項、科里奧利力和向心力項、重力項的方程帶入式(9)中計算各關節驅動力矩方程，即

(12)

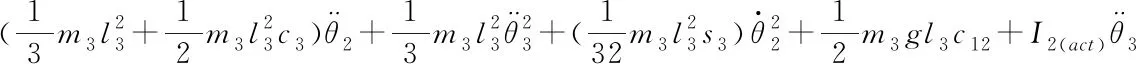
(13)

根據上述分析，完成了碼垛機械臂關節速度糾偏運動規劃。

4 實驗分析

4.1 實驗環境和參數設計

采用實物碼垛作業進行速度糾偏運動規劃實驗，碼垛機械臂為某大型公司工程樣機實驗平臺，如圖4所示。

圖4 碼垛機械臂實驗對象

實驗條件：抓取對象重量為35 kg，直線上升高度385 mm，下降高度185 mm，機械臂運行參數如表1所示。

表1 運動參數約束

在碼垛機械臂的運行軌跡上設置磁條軌跡，并在運動軌跡上安放四個大小為200 mm×200 mm的白色標記作為監測點，保證白色記號與磁條各自中心相重合，根據實際運行軌跡在白色標記上留下的痕跡作為驗證偏差情況。

4.2 結果分析

為驗證本文方法的有效行，實驗中設置不同偏差比例系數進行實驗，以磁條中心為界，偏左側為正值，偏右側為負值，測試點與標準軌跡間的偏差如表2所示。

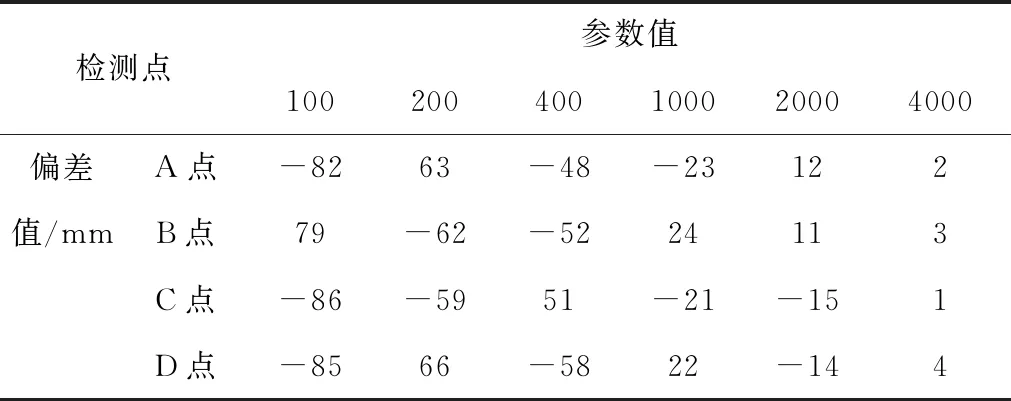
表2 偏差距離表

由表2可知，當偏差比例系數為4000時，本文方法能夠將偏差控制在±5mm之內，根據多次實驗過程中實際運行軌跡，基本與標準軌跡能夠保持一致，證明本文方法在碼垛機械臂關機速度糾偏運動中的控制效果較好，具有較好的應用效果和適用性。

針對Ⅰ軸和Ⅱ軸關節角、角速度和角加速度的軌跡曲線，通過四線運動連續性條件和MATLAB軟件編程繪制，具體軌跡曲線如圖5所示。

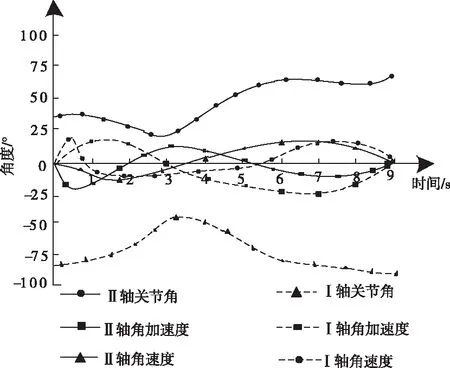
圖5 Ⅰ軸和Ⅱ軸軌跡曲線

由圖5可知，在運動控制過程中所有關節角、角速度和角加速度軌跡曲線均連續且光滑，可有效避免關節變向運動的沖擊，確保碼垛機械臂平穩運行，有效提升各關節運行學性能，提升碼垛機械臂工作效率。

為了進一步驗證所提方法的有效性，實驗對比本文方法、文獻[6]局部閉鏈碼垛機器人運動學分析及軌跡規劃方法和文獻[7]基于三次樣條曲線的碼垛機器人平滑軌跡規劃方法，對目標進行識別。在碼垛機械臂運動軌跡前置放規格為600×300×300mm的50個紙箱和一個400×350×280mm的紙箱作為識別對象，以成功抓取400×350×280mm的紙箱為目標，目標識別速度對比如圖6所示。

圖6 目標識別速度對比

由圖6可知，在碼垛機械臂目標識過程中本文方法的平均識別時間是±0.04秒，文獻[6]方法的平均識別時間為±0.12秒，文獻[7]方法的平均識別時間為±0.10秒，根據識別時間驗證了本文方法在目標識別速度具有較明顯優勢，表明本文方法控制下的碼垛機械臂的任務完成度和工作效率得到有效提升。

采用三種方法進行對600×300×300mm的紙箱進行碼垛實驗，三種方法碼垛用時和抓取精準度對比結果如表3所示。

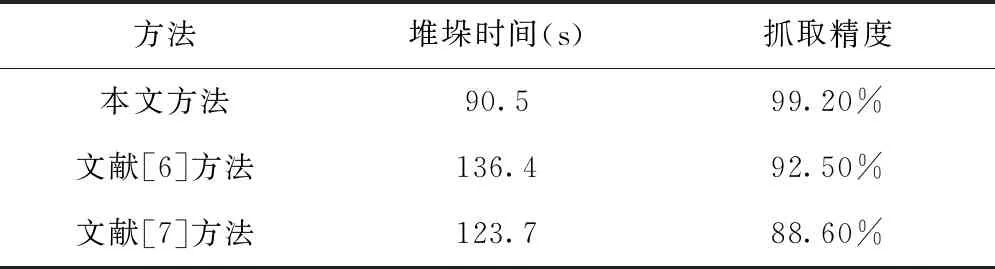
表3 碼垛用時和抓取精準度對比結果統計表

由表3可知，在堆垛過程中，本文方法與兩種對比方法相比效率分別提升了33.6%和26.8%，抓取精度分別提高6.7%和10.6%，表明采用本文方法對碼垛機械臂關節進行糾偏運動規劃能夠有效提高該機器人的工作效率，具有較高的實際應用價值。

5 結論

本文提出基于SSD的碼垛機械臂關節速度糾偏運動規劃方法。利用SSD算法進行對目標障礙物進行自主智能識別，為后期碼垛機械臂工作提供運動方向，完成碼垛機械臂關節速度糾偏運動規劃。采用本文方法能夠將偏差控制在±5mm之內，且碼垛耗時較短。