基于改進的PSO優化SVR的機場道面積冰預測

王立文，劉建華，陳 斌，李慶真

(1.中國民航大學航空地面特種設備研究基地，天津 300300;2.中國民航大學電子信息與自動化學院，天津 300300)

1 引言

機場跑道積冰是由于跑道表面有積水/降雪融化且在道面溫度下降到冰點，或者凍雨直接滴落到冷表面形成冰層。在我國冬季西北、華北、東北和云貴等地區是重冰區，從以往的數據觀察部分地區年均冰凍日數甚至在5天以上[1]，經常會遇到機場跑道結冰的情況，道面積冰會大大降低跑道的抗滑性，且在冰水混合情況下摩擦系數與冰層厚度是正相關關系[2]。在我國民航大發展的情況下勢必會給航空運輸行業帶來巨大的挑戰，影響機場的正常運營和旅客的出行計劃，因此，對機場跑道積冰厚度預測是十分必要的。

目前，國內外許多學者對積冰預測問題主要圍繞以下幾個方面進行研究，一是傳熱傳質解析模型，利用傳熱傳質學等知識對積冰過程進行分析，如Xiaomin Wu[3]等人在冷卻塊上利用結霜機理建立了相變傳質模型，該模型描述了濕空氣中水蒸氣的傳質過程，對霜冰的生長和致密化進行預測。杜雁霞[4]等人對飛機飛行過程中結冰過程的液/固相變傳熱特性進行了分析，建立了液膜及冰層生長模型。Ping Fu[5]， Pavlo Sokolov[6]對物體積冰的邊界層效應進行邊界層研究，并分析了液滴碰撞和分布譜效應，估算局部碰撞系數利用CFD工具數值模擬冰厚。二是數據統計分析，通過模擬積冰的環境或根據氣象站采集到的數據觀察積冰的過程，利用實驗結果分析各實驗條件對積冰的厚度或速率的影響再利用智能算法進行預測。如朱寶林[7]、熊竹[8]等人通過積冰環境模擬實驗室，模擬了積冰形成的溫度、濕度、風向、風速等環境條件，開展積冰的物理特征研究，并將引入的氣象因素用貝葉斯理論或神經網絡進行積冰預測分析；黃新波[8]、王玉鑫[10]，根據導線覆冰的模糊性，采集影響覆冰變化的氣象因子數據信息，與導線覆冰的模糊邏輯建立的模糊規則理論對積冰厚度進行預測；羅毅[11]根據采集的歷史氣象因子數據與氣象預測數據，根據神經網絡非線性映射變量關系對積冰厚度進行預測。三是積冰探測預測技術，將結冰探測器和氣象傳感器相結合并將算法嵌入，搭建積冰預測系統。N.Bezrukova[12]等人在自動道路氣象站使用一組傳感器測量空氣溫度、相對濕度、降水類型和強度、風速、路面干濕狀態等信息，將這些信息作為輸入，用熱平衡方程預測道面溫度，再根據預測道面的溫度信息和其它一些數據對道面積冰進行預測；尹麒煥[13]將環境溫度、空氣濕度、風速、風向、大氣壓力等參數綜合考慮，并開發了結冰傳感器，搭建基于多參數的道路結冰安全預警系統；許一飛[14]等人利用同軸和楔形兩種光纖傳感器，結合對射式傳感器、溫度等傳感器構成結冰檢測系統，而后根據各傳感器數據進行數據融合，達到識別冰型，測量冰厚的目的。

綜上3種研究方法，基于理論分析和數值模擬建立的模型可以從本質上反映各因素對道路積冰的影響，但是參數復雜且大多數參數通過經驗獲得，對模型的正確性有一定的影響；數據統計方法建立的模型通過數據分析積冰影響因子，建立積冰同相關因素的模型進行預測，但該類方法針對固定的區域且氣候變化趨勢相對穩定的情況下具有較好的預測結果，模型的泛化能力較差，這就要選擇泛化能力高的預測模型提高預測模型的精度；積冰探測/預測方法主要依靠路旁氣象傳感器和路面積冰傳感器采集的數據，但由于機場安全性要求較高不適合機場道面環境。本文設計室內模擬實驗，通過控制溫度、濕度、降雨量和風速4個影響積冰的氣象因子，用正交實驗法進行方案設計。支持向量機等數據挖掘技術針對高維非線性的模式識別問題表現出許多特有的優勢。采用支持向量機對積冰非線性增長過程進行回歸建模，同時，為提高支持向量機的預測精度使用粒子群算法對懲罰參數C與核函數參數g進行尋優。為避免粒子群算法陷入局部最優解和過早收斂的問題，對其模型中兩個學習因子采用時變異步變化時的經典范圍進行了改進并且加入了線性遞減的慣性權值。根據預測結果可知采用改進的粒子群算法對支持向量機進行尋優的準確度較高。

2 算法基本原理

2.1 支持向量回歸算法

支持向量回歸是建立在SVM基礎上的回歸算法。通過非線性映射把輸入空間的輸入向量映射到特征空間，之后在特征空間進行線性回歸，構造決策函數

f(xi)=ωTxi+b

(1)

為了解決SVM回歸擬合的問題，Vapnik等人在SVM分類基礎上引入了ε-不敏感損失函數，從而得到了回歸支持向量機(Support Vector Machine for Regression， SVR)。ε-不敏感損失函數的形式如下

(2)

根據結構風險最小化原則，得到線性回歸的凸二次規劃問題，由于在間隔帶兩側的松弛程度有所不同，所以引入松弛變量ξi和i得到如下公式

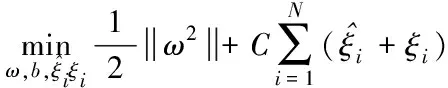
(3)

式中：C為懲罰因子。對于該問題的求解，經過引入拉格朗日函數，最終可轉化為對偶問題

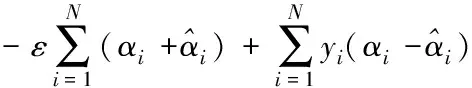
(4)

此時，對于非線性回歸需使用核函數把非線性數據映射到一個高維特征空間，然后進行線性回歸。回歸函數為

(5)

核函數采用高斯核函數即

K(xi，xj)=e-g‖xi-xj‖2

(6)

2.2 粒子群算法原理

粒子群算法是一種隨機尋優的群體智能算法，將搜索問題解的空間延伸到N維空間中。粒子群為由n個粒子組成的種群X=(X1，X2，X3，…Xn);微粒i在N維空間里的位置和速度都表示為一個矢量，第i個粒子位置表示成一個D維向量Xi=(xi1，xi2，xi3，…xiD)T，粒子的速度為Vi=(νi1，νi2，νi3，…，νiD)T，粒子通過跟蹤個體極值和群體極值更新自身的速度和位置，其更新方式如下

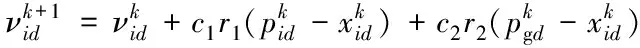
(7)

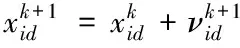
(8)

粒子的位置更新依靠上一步的位置和更新后的粒子速度，更加依靠速度更新，速度更新公式可分為3部分，第1部分為粒子前一時刻的速度；第2部分為粒子自身的思考能力，稱為“認知”部分，其中c1調節粒子飛向最佳個體位置方向的步長；第3部分表示為粒子之間的相互合作和信息共享，稱為“社會”部分，c2調節粒子飛向最佳群體位置方向的步長。

3 基于改進的PSO和SVR的積冰厚度預測方法

3.1 粒子群算法改進策略

由2.2節尾段指出粒子群尋優的關鍵在于學習因子c1和c2的值調節粒子移動的速度，進而影響粒子移動位置的步長。可在算法搜索初始階段使用較大的c1值和較小的c2值，使粒子減少受到局部極值的影響，可以增加粒子的多樣性；而后，在粒子搜索的后階段隨著迭代次數的增加，使用較小的c1值和較大的c2值，這樣就使得粒子容易收斂到全局最優。在文獻[15]中Ratnaweera根據迭代次數修改學習因子，采用式(9)和式(10)計算學習因子的值，進行實驗。根據實驗結果表明當c1∈[2.5，0.5]與c2∈[0.5，2.5]時，算法的實驗效果最佳。這種方法雖然加速了算法收斂，但也極容易陷入局部最值，適用于單峰值函數但在多峰值函數中容易過早收斂。

(9)

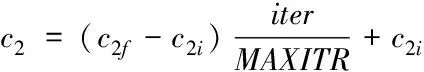
(10)

c1i和c1f分別為c1初始值和終值，c2i和c2f分別為c2初始值和終值，iter為當前迭代次數，MAXITR為最大迭代次數。

針對此問題在文獻[16]中對c1和c2的區間值進行改進，c1∈[2.75，1.25]和c2∈[0.5，2.25]，并在此基礎上引入了線性遞減慣性權重ω。因為初始時刻慣性權重較大，全局尋優能力較強，局部尋優能力較弱；且隨著慣性權重減小，局部尋優能力增強，全局尋優能力減弱，慣性權重如式(11)遞減。ω∈[0.9，0.4]，通過實驗測試效果較優。粒子群迭代尋優速度如式(12)。

(11)

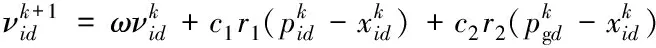
(12)

其中c1∈[2.75，1.25]，c2∈[0.5，2.25]，ω∈[0.9，0.4]。

3.2 改進的PSO-SVR預測模型

基于改進PSO算法的SVR預測模型，采用優化后的粒子群算法對SVR的懲罰參數C和高斯核函數的寬度系數g進行參數尋優。其中懲罰參數C反映了算法對超出ε的樣本數據的懲罰程度，會對模型的復雜性和穩定性造成影響，若C過小對遠離ε的樣本數據懲罰就小，造成訓練誤差變大，學習精度降低，對新數據處理的結果會變差；若C過大時，樣本的訓練精度提高，但模型的泛化能力變差。所以C值影響對樣本中非正常數據點的處理，選取合適的C值能在一定程度上抗干擾，保證模型的穩定性。寬度系數g反映了向量之間的相關程度，g太小向量間的相關程度較小且推廣能力較弱；g太大，向量間的影響就越大，但是會對回歸模型的精度造成影響。

其中預測后的誤差用均方誤差表示

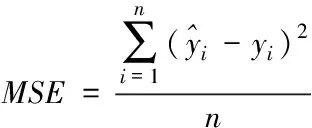
(13)

基于改進PSO對SVR的參數(C，g)進行尋優并建立預測模型的步驟如下：

Step1：初始化粒子群相關參數。設定種群的規模、迭代次數和慣性權值，搜索的邊界。對兩個參數(C，g)的位置和速度進行初始化，并設置粒子初始時的個體最優位置pbest和群體最優位置gbest。

Step2：根據設置的適應度函數式(13)求出各粒子的初始適應度值。

Step3：再由優化后的粒子群算法速度更新式(12)和位置更新式(8)進行更新粒子的位置和速度。

Step4：根據適應度函數計算適應度值，更新粒子個體最優解和全局最優解。

Step5：判定優化后的粒子群算法是否達到結束的條件，若是，結束搜索，返回全局最優位置參數向量(C，g)；若否，轉到Step2繼續執行。

Step6：基于上一步返回的參數向量(C，g)建立SVR積冰預測模型。

4 實驗及仿真結果分析

4.1 實驗系統設計

由于氣象條件的復雜性與積冰環境的多樣性，機場道面積冰現象很難在實際的環境中進行及時的觀測，因此僅僅依靠室外進行實驗設計不能控制外部的實驗環境不能保證實驗的可重復性，數據的對比分析以及實驗結果也不能做到全面和深層次的理解。本文借助人工氣象環境室搭建環境模擬系統借助機場環境模擬實驗平臺對機場道面積冰過程進行模擬實驗和數據分析。實驗系統結構圖如圖1。

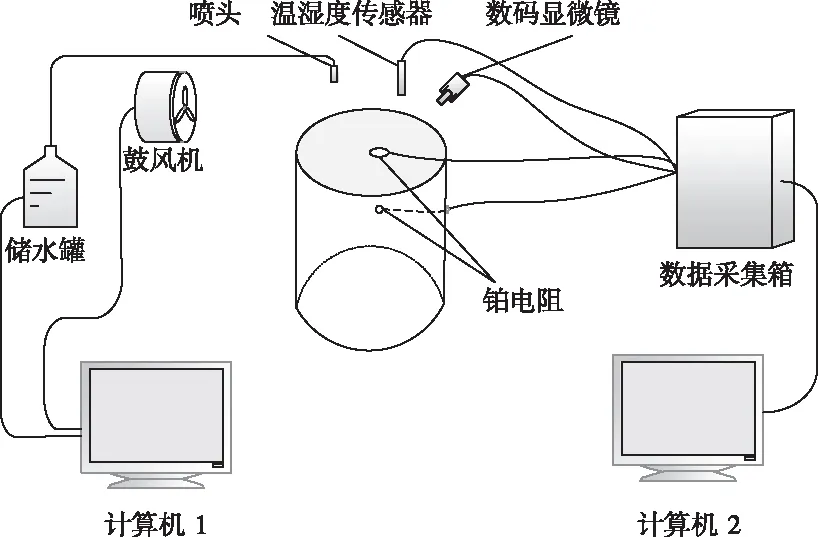
圖1 機場道面積冰實驗系統結構圖

機場環境模擬實驗平臺為積冰實驗中冰層厚度的數據采集平臺，機場環境模擬實驗平臺積冰效果圖，如圖2。實驗中測量積冰厚度所采用的的儀器為Dino-Lite手持式數碼顯微鏡，將其對準實驗平臺對冰層進行拍照，對照片中的冰層厚度進行測量，測量精度為0.001mm。

圖2 數碼顯微鏡下的積冰厚度測量圖

4.2 實驗方案設計與分析

由于機場跑道積冰受多參數影響，探究在多環境耦合作用下的積冰影響效果，本文采用正交實驗法進行實驗方案設計。正交實驗法具有正交性、均衡性和獨立性的特點，可以方便設計實驗盡可能減少實驗次數，使用數理統計的方法處理實驗結果分清因素的主次。在搭建好的實驗系統中，通過將溫度、濕度、風速和降雨量這4個影響積冰的氣象因子控制在一定范圍內，根據正交實驗法進行合理的實驗設計。在所設置的實驗中將溫度、濕度、風速和降雨量選取三個水平，如表1。

表1 機場跑道積冰實驗參數水平表

對四個積冰氣象因子選取的三個水平設計正交實驗表，以實驗最終的積冰厚度作為評價指標。根據機場跑道積冰實驗參數水平表，采用L934設計正交實驗，各參數在不同水平下的積冰厚度如表2所示。

由于積冰因素較多且積冰環境較復雜很難做到科學定性定量的研究機場跑道的積冰現象，需要合理的簡化方案對實驗環境作出假設：整個實驗環境中空氣溫度和相對濕度相對穩定；風速和降雨量均勻固定，且整個系統的空氣主流速恒定不變。

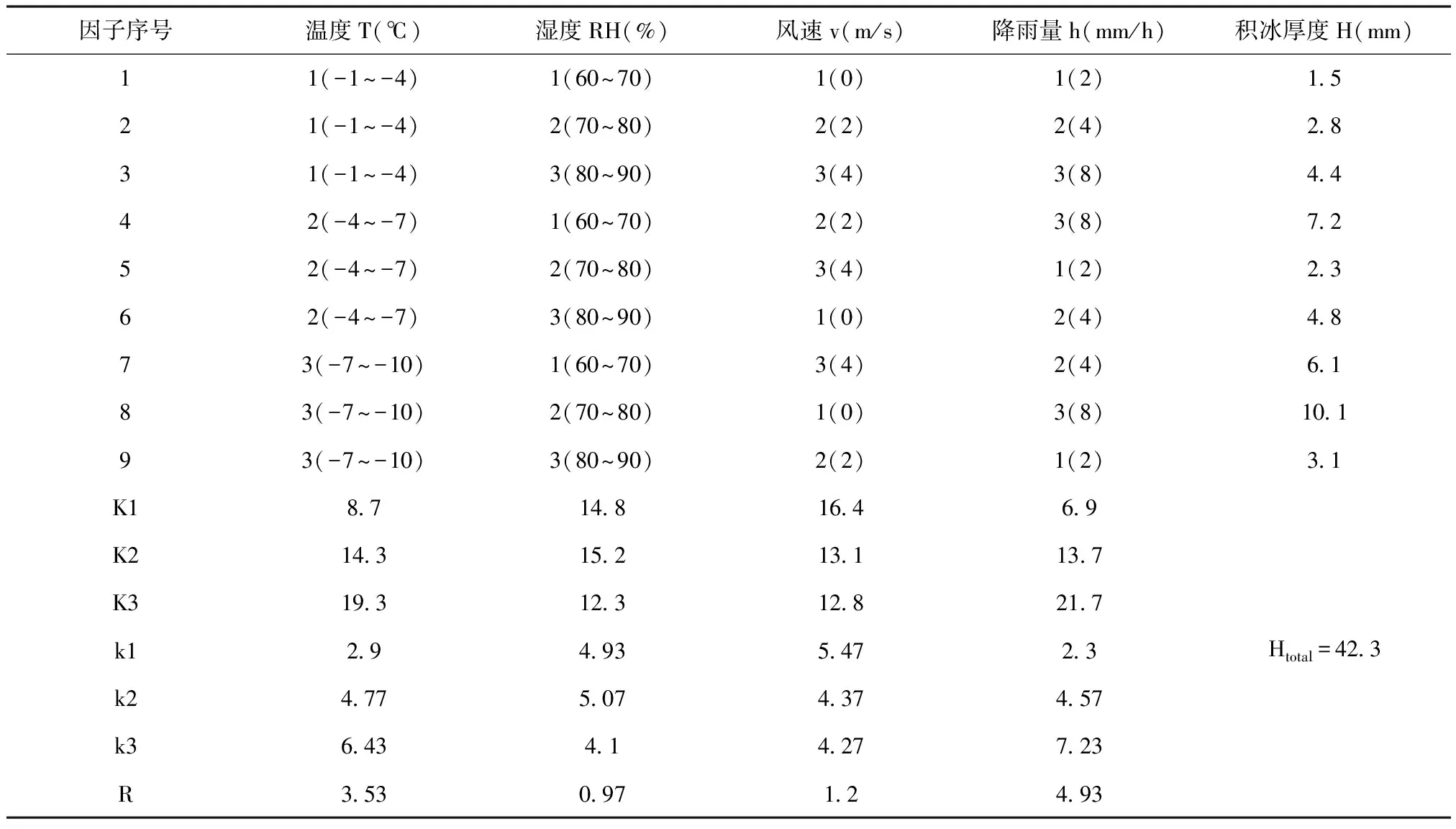
表2 實驗方案表

通過使用極差分析法對實驗進行分析，可以確定各積冰影響因子作用時對積冰厚度的影響。通過比較極差來判定影響程度的大小，極差R越大就表明該氣象因子對積冰的影響越大。

R=max(k1，k2，k3)-min(k1，k2，k3)

(15)

其中：ki=Ki/3，i=1，2，3。Ki是各積冰影響因子的第i水平的積冰厚度，ki是各積冰影響因子的第i水平的平均積冰厚度。通過極差分析得到各積冰影響因子對積冰的影響程度由大到小依次為：降雨量﹥溫度﹥風速﹥濕度。為直觀起見，以參數的水平作為橫坐標，以影響積冰厚度的平均值作為縱坐標，氣象因子與影響積冰趨勢圖如圖3所示。

積冰影響因子較多且呈現非線性變化，積冰厚度跟隨影響因子的變化而變化。從圖3可以看出，隨著溫度的降低和降雨量的增加，積冰厚度呈現不斷上漲的趨勢，且在溫度最低和降雨量最大的時候積冰厚度達到最大值，同水平的積冰厚度平均值占用縱坐標的范圍較大，說明這兩個參數對積冰厚度的增長是非常敏感的，隨著溫度、降雨量的變化積冰厚度有較大的變化。在隨著風速、濕度變化時，積冰厚度只在較小的范圍內波動，說明風速、濕度對積冰厚度敏感度較低。

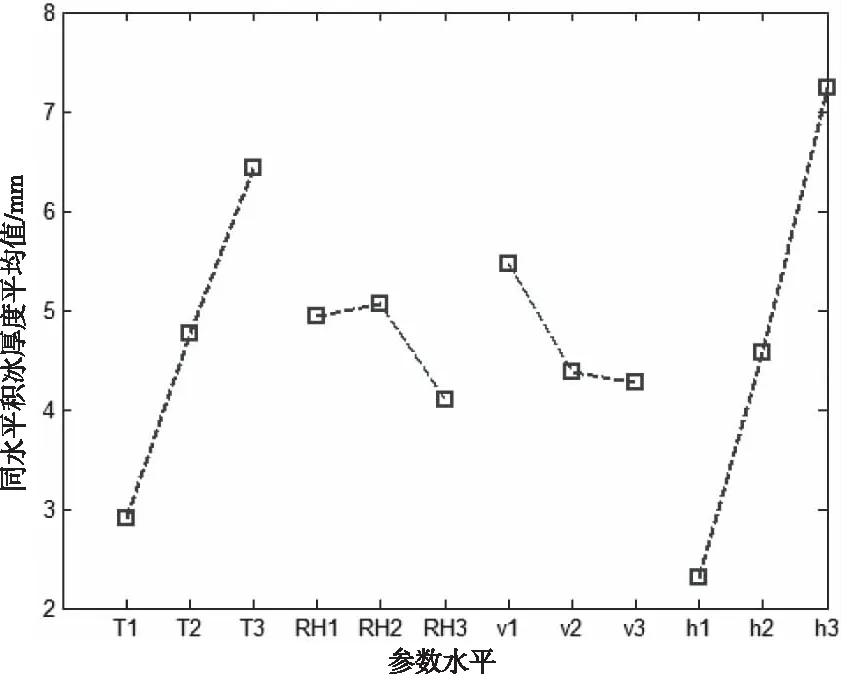
圖3 氣象因子與影響積冰趨勢圖

4.3 仿真結果對比分析

根據正交實驗法設計的方案，在該方案下設計實驗參數進行實驗，控制溫度、濕度、風速和降雨量四個變量。由于熱量守恒的作用中間道面溫度和道面表面的溫度對積冰厚度有影響，故另外采集了道面溫度、中間道面溫度和積冰厚度數據，綜合以上數據為輸入，積冰厚度為輸出，通過該模型訓練測試對未來20分鐘的積冰厚度進行預測。

粒子群算法對支持向量回歸尋優初始時需對參數的尋優范圍、種群數目和迭代次數進行設置，保證每組的仿真尋優初始參數設置相同，方便仿真結果作對比。算法尋優的初始參數設置如下：終止迭代數為1000，種群數目為30，支持向量機C、g的取值范圍為c∈[0.1，1000]，g∈[0.01，100]，ε為0.001。

為比較本文優化方法的效果，除上述初始時的參數設置相同，還要在相同的設備，相同的數據量下運行比較。另外文中選用BP神經網絡來進行對比。為了更直觀的說明改進PSO-SVR的優越性能，模型的誤差檢驗采用均方誤差(MSE)的評價指標來反映3種建模方法的效果，表3給出了3種方法對積冰厚度預測效果的對比情況。由表3中可以看出BP神經網絡的平均誤差率為0.38%，Ratnaweera PSO-SVR的平均誤差率為0.31%，改進的PSO-SVR的平均誤差率為0.27%誤差率最小，改進的PSO-SVR預測效果最佳。圖4展示了本文預測方法的結果與BP神經網絡、Ratnaweera PSO-SVR的對比圖。

表3 不同建模方法的預測效果對比

5 結論

針對冬季機場在凍雨條件下道面積冰厚度的問題，根據正交實驗法設計了實驗方案，建立了改進的PSO-SVR預測模型，對機場道面未來20分鐘積冰厚度進行了預測，得到如下結論：

1)搭建了室內模擬實驗系統，保證實驗環境溫、濕度、風速和降雨量的可控性，另外采集了道面溫度和中間道面溫度的數據，保證了數據的可靠性，為模型的建立做準備。使用正交實驗法進行實驗方案設計，根據極差分析法極差R的大小，分析影響積冰厚度的影響因子主次順序為：降雨量-溫度-風速-濕度。

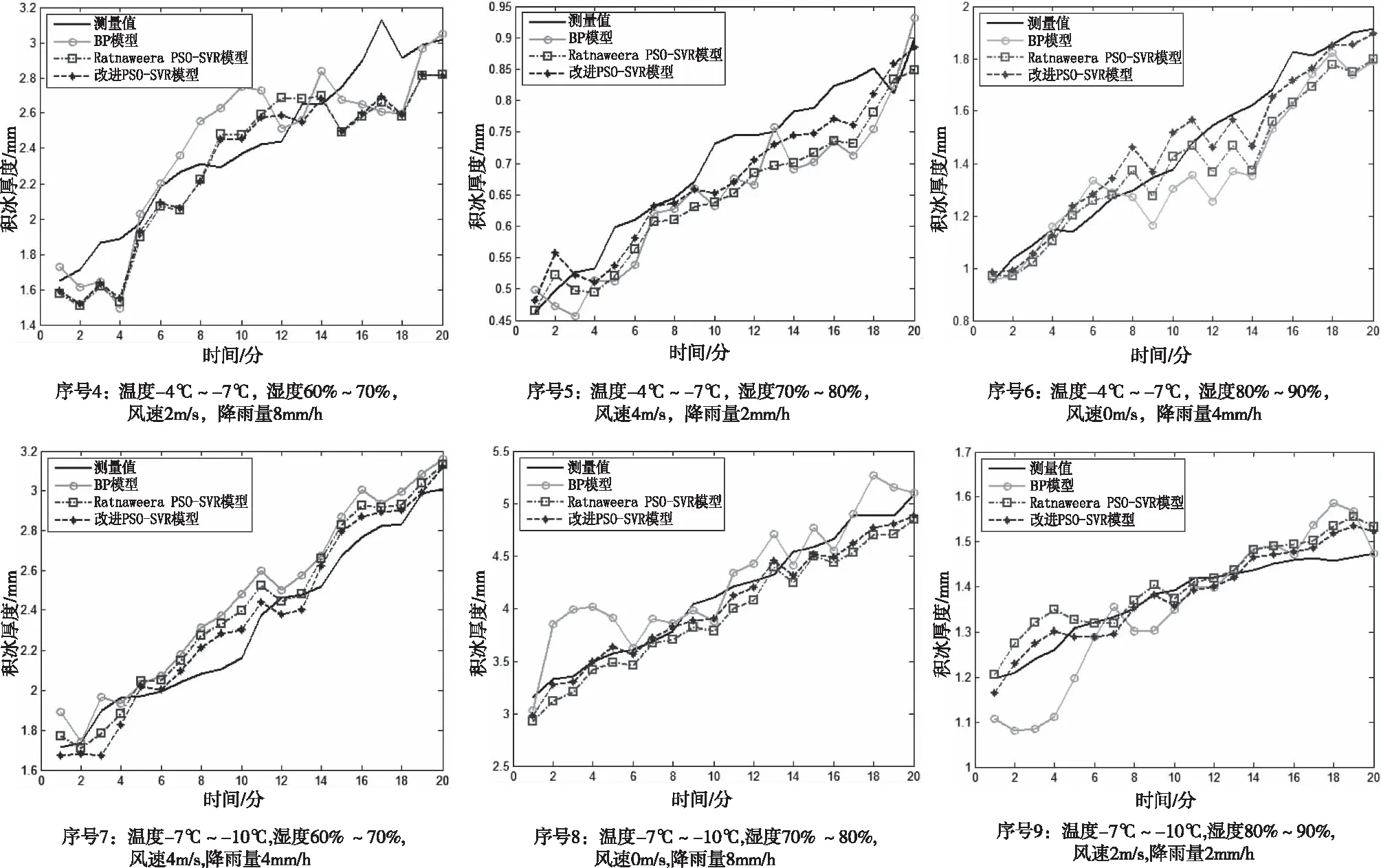
圖4 預測結果對比圖

2)針對SVR參數尋優困難的問題使用粒子群對支其進行參數尋優。同時粒子群算法在參數尋優的過程中易陷入局部最優和過早收斂的問題，提出使用權重遞減的方法和改善學習因子范圍的方法改善粒子群算法。通過仿真結果表明改進的PSO-SVR優化效果最佳，其平均誤差率由BP神經網絡的0.38%降低到0.27%，平均誤差率降低了0.11%。將該模型用于機場積冰的預測，可為機場的運行管理提供依據。