PID控制器中隨機干擾控制方法的設計與實現

陳燦輝，黃春慶

(廈門大學航空航天學院，福建 廈門 361005)

1 引言

輸出方差是過程控制系統的主要性能指標之一[1，2]。由于PID控制器結構簡單易于實現的優點，至今仍然為大多數工業控制回路所采用[4]。受PID控制器結構限制，PID控制器無法完全實現最小方差(Minimum Variance， MV)控制的性能[2，3]。因此，近似實現最小方差控制的PID控制器(MV-PID)參數整定問題是值得研究的問題。

傳統的PID參數整定法如Z-N法、繼電反饋法、階躍響應法和極點配置法等[5]，是基于時域的性能指標如超調量、響應時間和調節時間等作為性能指標進行整定參數的，通常把參數整定問題轉化為基于性能指標的一個優化問題、并通過求解優化問題獲得參數整定。基于最小方差PID控制器參數整定問題也可以采用類似的方法進行求解。Ko和Edgar[6]提出了一種基于過程輸出數據和過程模型的梯度基方法來實現最優PID控制器參數整定； Kariwala[7]提出一種解析下界法，通過選擇擾動到輸出之間的閉環傳遞函數的兩倍時延項脈沖響應系數，來獲得PID參數和相應的PID可實現的最小方差；Shahni和Malwatkar[2]提出了一種利用MathWorks優化工具函數fminco實現PID優化設置的簡單方法；Huang和Huang[8]提出利用牛頓迭代方法求出PID控制系統的最小輸出方差以及相應的最優PID參數。Dickinson和Shenton[9]提出了一種參數空間技術，將現有魯棒控制技術中的參數空間邊界進行疊加，從而實現非保守魯棒最小方差PID設計。由于最小方差PID控制器參數整定的優化問題是非凸的，因此上述的優化算法對初值選取均有比較高的要求。如果初值選擇不當，只能得到局部最優解[3，10]。顯然，選擇適當的初值并非易事[3]。

針對隨機干擾下的MV-PID控制器參數整定問題，考慮其優化問題的非凸性，采用粒子群算法以獲取全局最優解。目前，基于粒子群算法的PID參數(PID-PSO)整定方法，基本上是利用PSO的全局尋優特點找到使系統超調量最小、穩定時間最短、上升時間最小等幾個描述系統動態性能的指標最優化及系統穩態誤差最優的PID控制器參數[11-14]，實際上，對于過程控制系統而言，更關心的是抗干擾的性能。因此本文在利用粒子群算法求解上述提到的非凸優化問題目的在于保證系統穩定的前提下，得到系統的最小輸出方差，并用仿真算例驗證了本文方法的有效性。

2 MV-PID控制器參數整定

考慮離散反饋控制系統如圖1所示，閉環輸出可以表示為[3，8]

y(t)=G(q-1)u(t)+N(q-1)a(t)

(1)

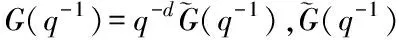
一般地，PID控制器 采用標準離散結構

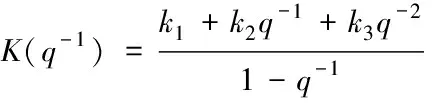
(2)

其中k1，k2，k3為待整定的控制器參數。

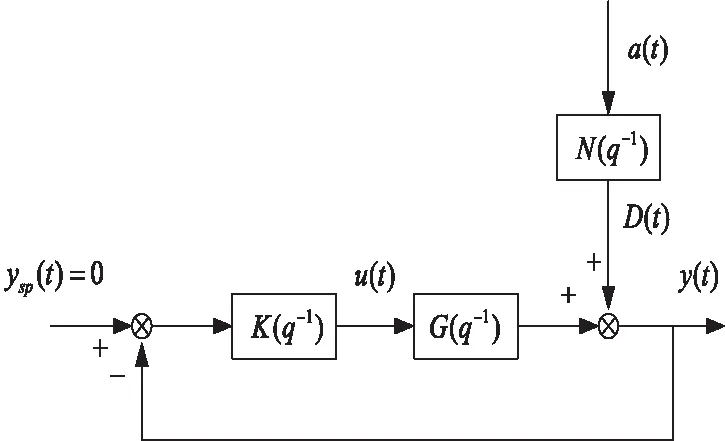
圖1 典型單回路反饋系統

當參考信號ysp(t)=0時，擾動源a(t)到輸出y(t)傳遞函數表示為[3，8]

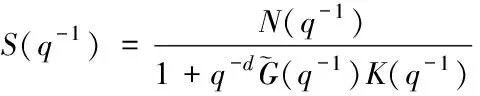
(3)

由于a(t)方差為1，可知系統輸出方差為[3]

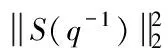
(4)

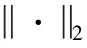
考慮如圖-1隨機擾動下的過程控制系統，控制器的設計目標是使得閉環系統的抗干擾性能最優。于是，基于最優輸出方差性能的PID控制器參數I={k1，k2，k3}整定可表示為如下優化問題

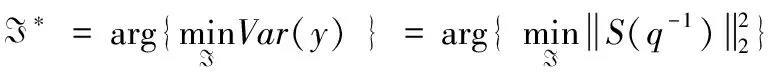
(5)

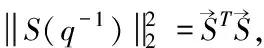
(6)

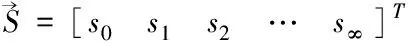
(7)

其中si是閉環傳遞函數S(q-1)的脈沖響應系數。當S(q-1)的所有極點均位于單位圓內時，對于足夠大的i，si將近似于0。事實上，根據文獻[2]，當i足夠大即i>4d(其中d為受控對象時延)時，式(6)可近似為

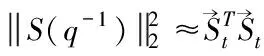
(8)

其中

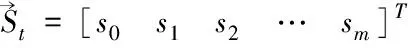
(9)

相應地，優化問題轉化為

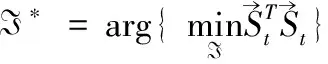
(10)

為了計算方便起見，將控制器中的積分環節與對象模型G合并為

(11)

于是得到如下關系式

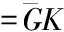
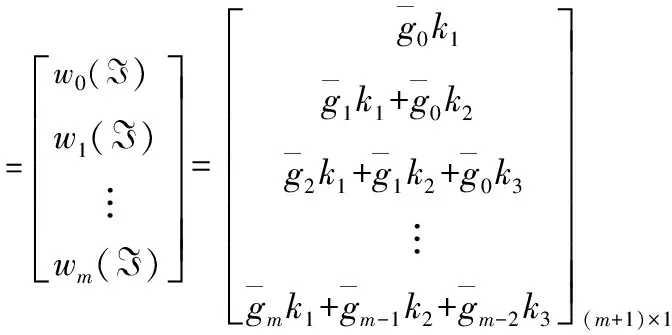
(12)

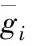
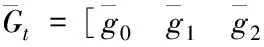
(13)

從而

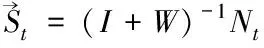
(14)

其中Nt為擾動傳遞函數的脈沖響應系數向量，即

Nt=[n0n1n2…nm]T

(15)

W為m×m維矩陣，其中wi為矩陣的第i階元素

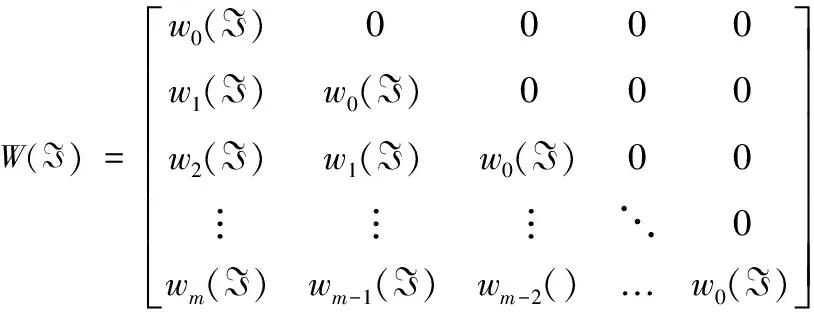
(16)

因此通過求解由式(14)所表征的優化問題(10)，可獲得最小方差的PID 控制器最優參數。

3 參數整定優化問題粒子群算法

由于式(10)優化問題的非凸性，傳統的凸方法求解往往不能獲得全局最優解。考慮到粒子群算法(Particle Swarm Optimization， PSO)具有的優點：搜索速度快，結構簡單且易于實現；不依賴優化問題本身的嚴格數學性質，且能夠求得問題的全局最優解，因此在求解MV-PID控制器參數整定問題上比其它迭代優化算法更有優勢[15，16]。

給出MV-PID的完整帶約束優化問題如下

s.tPL≤k1≤PU；IL≤k2≤IU；DL≤k3≤DU；

(17)

其中PL和PU、IL和IU、DL和DU分別表示PID控制器控制的對應三個參數的約束范圍，與此同時，所給的PID參數需要保證系統穩定。

常規的粒子群算法流程主要由以下幾個步驟[14，15]：初始化、個體極值與全局最優解、更新速度和位置公式以及終止條件判斷。給出各步驟具體內容：

1)初始化：

①確定迭代次數g和種群大小n；

②目標函數的自變量個數d；

2)個體極值與全局最優解：

①定義適應度函數f；

②個體極值為單個粒子找到的最優解，即最小方差；

③從所有種群中找到最優解然后進行迭代更新；

3)更新位置和速度：

速度公式

Vid=ωVid+C1random(0，1)(Pid-Xid)

位置公式：Xid=Xid+Vid

其中ω為慣性因子，其值非負，較大時全局尋優能力強，較小時局部尋優能力強；C1為個體學習因子；C2為社會學習因子；Pid表示第i個變量的個體極值第d維；Pgd表示全局最優解的第d維；Vid表示第i個標量的個體極值第d維的速度；Xid表示第i個變量的個體極值第d維的位置。

4)終止條件：達到迭代次數即終止，否則返回第2)步。

4 仿真算例

本文的仿真，參照文獻[3]中提供了十個仿真算例，如表1所示。通過本文所提出的算法求解，獲得的最優PID參數整定如表3所示；并將本文的計算結果與文獻[3]的結果作對比，相應的最小方差值，均列于表3。具體算法過程說明如下：

表1 仿真算例

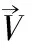
通過Matlab仿真軟件實現粒子群算法并求解式(10)中的優化問題，其中在搜索空間內隨機生成種群時，結合具體系統特征，應保證離散反饋控制系統穩定，即系統的特征方程的根均在單位圓內。在表1算例3，4，5，6中，(在不考慮計算時間開銷及計算復雜度的情況下，為了保證整定參數準確性，需要擴大種群的大小)，若是考慮算法的快速性以及結果的準確性，可以將搜索空間M改成：[0， 1]、[-2， 0]和[0， 1]，種群的大小則不需要改變。仿真結果如下：

表2 參數設置

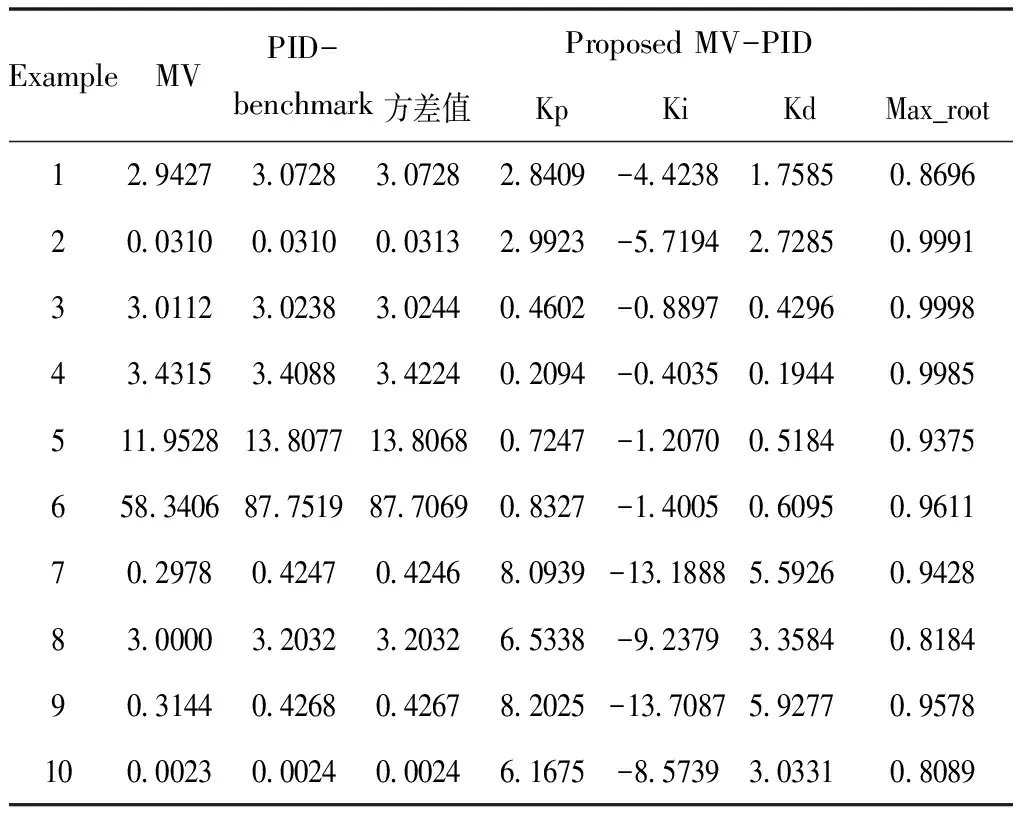
表3 仿真結果比較

表3中，MV表示線性最小方差的理論值；PID-Benchmark表示文獻[3]所設計最小方差PID的輸出方差值，常常被引為比較基準；本文利用粒子群算法得到結果列于表格右側，其中列Max_root表示相應的閉環系統特征方程根的最大幅值。

由表3中的仿真結果可見，本文所提出方法獲得的閉環系統最終輸出方差，與文獻[3]的PID-Benchmark，差別幾乎可以忽略不計，表明了通過粒子群算法來計算MV-PID參數整定是可行且有效。相較其它的迭代優化算法來說，粒子群算法能夠在全局范圍內搜索優化問題的最優解，避開局部最優解，使所求解的PID參數在滿足系統穩定的前提下，最小化系統的輸出方差。

5 結論

當噪聲源至閉環輸出的傳遞函數滿足穩定條件時，PID參數整定問題可轉化為一個非凸優化問題。由于該問題的非凸性，常規優化方法往往無法得到全局最優解。本文采用粒子群算法，獲得該非凸優化問題的全局解，從而解決了MV-PID控制器參數整定問題。通過多個仿真算例，應用本文算法進行參數整定，其控制效果幾乎與理想最小方差控制一致，從而驗證了本文算法的有效性，為MV-PID控制器參數整定問題提供了另外一種值得推薦的選擇。