基于無限深度神經網絡的Web大數據協同過濾

葛 涵，張志勇，張紅良

(北華大學文學院，吉林 吉林 132013)

1 引言

互聯網用戶快速增長與網絡數據規模不斷擴大，使人們從信息匱乏時代逐漸步入信息化時代，同時促使了Web社區層出不窮，作為社交網絡的關鍵組成部分，其發展速度持續高漲。Web本意指蜘蛛網與網的意思，在網絡中稱其為網頁。越來越多用戶因為興趣匯集到Web社區中。在滿足人們互動需求的同時也帶來了信息過載問題，因此，推薦系統應運而生。信息創造者竭盡全力讓自己生產的信息在網絡中脫穎而出，獲得更多關注；同時，用戶也通過該系統獲取感興趣的信息。為改善推薦效果，提高用戶滿意度，數據過濾算法顯得尤為重要。

邢長征[1]等人將填補算法與改進的相似度算法相結合實現大數據協同過濾。首先采用填充方法任意填充部分數據，并在預測評分時融入項目屬性信息；再利用相似度方法，根據迭代多次后項目評分高低完成最終過濾。陶維成[2]等人提出灰色聚類協同過濾算法。定義推薦系統中用戶項目評分矩陣、灰色絕對關聯度與相似度等；確定灰色關聯聚類協同過濾算法計算步驟；最后將不同算法在規模不同的數據集下進行實驗。

上述兩種數據過濾算法改善了推薦系統性能，但是依舊存在數據稀疏等問題，導致數據過濾不夠全面，進而降低用戶體驗。為此，本文利用無限深度神經網絡算法實現Web大數據的協同過濾。深度神經網絡(Deep Neural Network，DNNs)與其學習方法，作為成功的數據分析算法，已經被各行業所熟知。和傳統算法相比，深度學習可以自動從數據中獲取特征，對形式多變的大數據具有較好的特征提取效果。而協同過濾可以實現基于內容的信息自動分析。將二者相結合可有效改善數據稀疏問題，同時提高算法的可擴展性，解決個性化推薦系統發展與應用瓶頸。

2 無限深度神經網絡

2.1 網絡拓撲結構

現階段深度神經網絡一般指存在一定深度的前饋網絡[3]，其特征是相同層次神經元之間不存在任何反饋連接，即沒有時間參數屬性，因此比較適合處理靜態信息。而本文利用的無限深度神經網絡則是一種完全互連形式的回復式神經網絡，不同神經元可實現反饋連接。同時將此種反饋結構在時間維度中展開，隨著時間推移，網絡能夠“無限深”。其本質屬于一個動力學系統，可以對與時間相關的動態數據加以處理，

針對無限神經網絡中所有神經元來講，其包括三種連接方式：神經元和全部外部輸入之間的連接、和其余全部神經元的連接、與自身的反饋連接。圖1與圖2分別展示了存在三個神經元、兩個外部輸入的網絡拓撲結構。

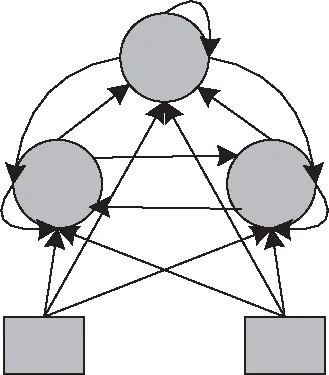
圖1 具有三個神經元的網絡結構圖

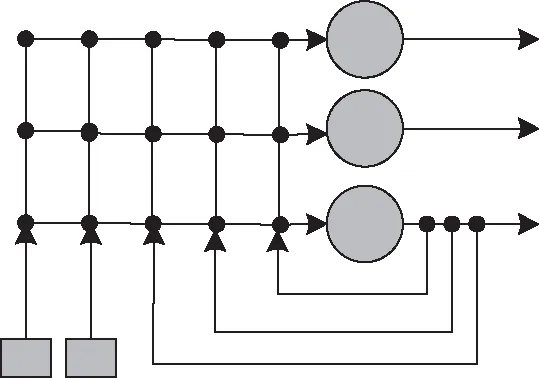
圖2 存在兩個外部輸入的網絡拓撲圖

假設某無限深度網絡包含m個外部輸入與n個神經元，設定x(t)=(x1(t)，x2(t)，…，xm(t))T表示網絡在t時間點上的外部輸入，y(t)=(y1(t)，y2(t)，…，yn(t))T代表t時間點上n個神經元輸出值。因此能夠得出，某神經元k在t+1時間上得到的總輸入sk(t+1)包括x(t)與y(t)兩部分。

假設w屬于網絡連接權值[4]，它是一個n×(n+m)矩陣，可令w=[wU，w1]，wU代表各神經元之間連接權值，w1為神經元和網絡外部二者的連接權值，則t+1時刻神經元的總輸入表示為

s(t+1)=wUy(t)+w1x(t)

(1)

式中，s(t+1)=(s1(t+1)，s2(t+1)，…，sn(t+1))，則t+1時刻神經元k的輸出公式[5]表示為

yk(t+1)=fk(sk(t+1))

(2)

式中，fk代表神經元k的激活函數。

為方便分析，將無限深度神經網絡反饋結構在時間維度上進行展開。假定某網絡N從t0時間點運行，任意一個網絡N均被展開為前窺式網絡N*中內一層。N*中所有層都具備n個神經元，并且和該時間點的網絡N存在相同的活動值。

針對任意τ≥τ0，網絡N中神經元j和τ+1層神經元i之間的連接權值wij被復制為網絡N*中τ層神經元j和τ+1層神經元i之間連接權值wij(τ+1)。

隨時間推移，N*的深度能夠“無限深”，此種狀況下將網絡稱作無限深度網絡。

2.2 學習過程

神經網絡的計算性能主要通過連接權值進行表現，所以，學習算法[6]即為調整網絡權值的方法，利用公式表示為

wnew+wold+Δw

(3)

權值調整目的是為使網絡學習到一些知識，幫助完成計算任務。一般將計算任務量化成對性能函數J(w)的優化，所以

wnew=wold+α?wJ

(4)

式中，α表示學習速度，?wJ代表性能函數在參數空間內梯度[7]。

通常來講，以某個學習任務為例，在t時刻，網絡中存在外部輸入x(t)與目標輸出d(t)。利用T(t)描述目標輸出是dk(t)的神經元集合。則t時刻網絡中神經元k的實際輸出和目標輸出二者誤差計算公式如下

(5)

神經網絡在t時刻的性能函數描述為

(6)

設定網絡運行的起止時間分別表示為t0與t1，而在時間[t0，t1]區間內，網絡整體性能函數表達式為

(7)

對于上述性能函數，必須通過一定方法對其訓練，減少誤差，提高網絡性能。本文利用反向傳播算法(Back Propagation，BP)對網絡進行訓練。該算法的限制條件為網絡中所有神經元結點的激活函數一定是可微的，是一種有監督的學習方法。

已知設計好的神經網絡中(W，b)為確定的，利用oout(x)代表輸出層的最終輸出，則神經網絡訓練過程如下

(8)

由式(8)可知，神經網絡將多個結點進行連接，展現了正向傳播過程。

如果用作訓練神經網絡的集合中包括N′個訓練樣本{(x(1)，y(1))，…，(x(N′)，y(N′))}，則其目標函數表示為

(9)

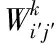
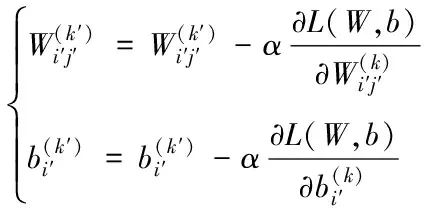
(10)

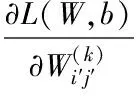
經過上述訓練，網絡隱藏層中所有的輸出不再敏感，減少誤差，降低網絡學習復雜度。

3 Web大數據協同過濾

利用上述訓練好的無限深度神經網絡分別對Web大數據的權重、梯度以及相似度進行計算，評價各個數據并進行排序，將排序靠后的大數據進行過濾。

3.1 權重

瀏覽次數可以體現出用戶對不同數據的感興趣程度，假設用戶u對Web大數據O的興趣度數值隨O被其他用戶瀏覽次數增而增加，同時又隨瀏覽頻率呈現反比下降趨勢。則可使用TF-IDF算法，結合瀏覽次數獲取用戶對大數據感興趣程度。

TF-IDF為一種估計字詞對于某文件集合中一份文件重要程度的算法。它能夠預測K′維空間內目標在某維度上的重要性。假設將推薦系統內任意用戶當作一個文檔，被用戶瀏覽的大數據為文檔中某一詞匯，針對詞匯出現次數來獲得用戶對該數據的喜好程度。

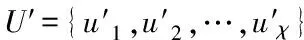
(11)

(12)

因此獲得用戶對數據權重的定義式

(13)

3.2 梯度

用戶對不同類型數據瀏覽次數存在較大差異。瀏覽次數能夠無限增加，同時對于瀏覽次數為零的數據，用戶也不一定不使用，可能是并無使用情況。為通過瀏覽次數更加科學的體現數據功能，避免海量信息將用戶對其它數據的使用情況忽略掉，本文為用戶沒有瀏覽的數據定義一個初始值，并引入Sigmoid函數對瀏覽次數進行標準化處理，獲得數據功能梯度。

Sigmoid函數為一個常見的S型函數，其定義式如下

(14)

此函數連續、光滑單調，并且其取值范圍為(0，1)，同時關于(0，0.5)中心對稱，屬于一個性能較優的閾值函數。在區間(-∞，0]中表現出現慢后塊的非線性增長趨勢，且在[0，+∞)區間中的增長態勢為先快后慢。

(15)

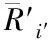
3.3 相似度

(16)

4 仿真分析

為分析基于無限深度神經網絡的Web大數據協同過濾有效性，選取Intel Core i36100，16GB RAM的配置處理器進行仿真。仿真過程中全部程序均利用Matlab實現。采用標準Web數據集作為研究目標，其中包含20000個用戶與25000條數據。由于數據規模較大，選取其中20%進行仿真。此外，將文獻[1]、文獻[2]算法與本文協同過濾算法，通過F-measure評價指標進行性能評價。

F-measure是信息檢索領域常用的評價標準，其中包括查全率(Recall)與準確率(Precision)，計算公式分別如下

(17)

(18)

公式中，E(u′)與F(u′)分別代表訓練與測試集合的過濾列表。

利用三種方法對實驗數據進行過濾，再通過推薦系統將過濾后的數據推薦給用戶，獲得查全率與用戶滿意度結果分別如圖3和4所示。

圖3 查全率對比圖

圖4 用戶滿意度對比圖

由圖3和4可知，通過本文方法過濾后的數據查全率較高，這是因為本文通過計算用戶興趣度與功能興趣度，全面掌握用戶喜好，解決數據稀疏問題，提高查全率。此外，在不同數據量下F-measure值也遠高于其方法，表明推薦效果良好，證明神經網絡模型具有超高性能，可減少過濾誤差，滿足用戶瀏覽需要。

除上述對比外，對不同方法響應時間進行測試，進一步增強所提方法實驗結果的說服力。

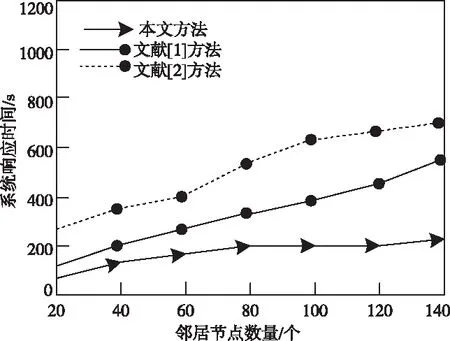
圖5 不同方法響應時間對比圖

從圖5中可以看出，本文方法隨著鄰居數量的增加，系統響應時間并沒有明顯上升趨勢，始終低于其方法。這是由于無限深度神經網絡學習過程較為簡便，減少計算用戶喜好程度的時間，實現高效過濾，進而減少系統響應時間。

5 結論

由于數據規模的不斷擴大，傳統過濾算法出現數據稀疏等問題。因此，本文利用無限深度神經網絡預測用戶對數據內容與功能的興趣度，根據興趣度高低實現Web大數據過濾。仿真結果表明，該方法查全率高，可改善數據稀疏現象，提高用戶滿意度。從當前發展來看，利用神經網絡技術建立過濾算法來提高推薦系統吞吐量是一個具有重要意義的研究方向，后期將在更大規模數據集中對算法的可拓展性進行測試，使其實現并行化。