指揮控制系統效能評估指標值灰色預測模型

余宏峰，李琳琳，肖 彬，金 明

(火箭軍工程大學作戰保障學院，陜西 西安 710025)

1 引言

預測性評估是指通過對評估對象的多個評估指標時間序列數據進行預測建模得到預測結果，將其運用于評估過程，實現對未來一段時間的狀態進行評估的一種新的評估方法，目前預測性評估已廣泛運用于醫療衛生、航天航空、金融和軍事等各個領域[1-3]。傳統評估方法與預測性評估方法流程對比如圖1所示。

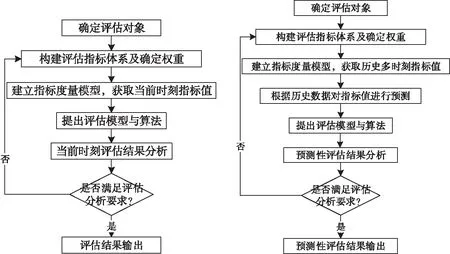
圖1 傳統效能評估方法流程圖(左)與效能預測性評估方法流程圖(右)對比

信息化戰爭下對指揮控制系統靈活性和敏捷性要求越來越高[4-5]，開展指揮控制系統效能預測性評估是提高評估結論準確性和系統敏捷性的重要手段，對系統總體效能的提升具有決定性作用，而評估指標值的預測結果作為預測性評估過程的數據輸入，對評估結果準確與否起著至關重要的作用。

信息化條件下指揮控制系統的信息復雜性不斷增長，其效能評估指標值呈現出混合數據類型的狀態，針對該問題目前有不同角度的處理方法[6-8]，對比這些處理方法后，本文綜合考慮效能評估指標值的特點，保留數據的完整性和不確定性，同時為了簡化計算和降低算法復雜度，采用將混合類型數據序列轉化成區間數序列的方法進行混合數據的處理。

指揮控制系統效能評估指標值序列的樣本量較小，且統一數據類型后的區間數本身具有一定的不確定性，而灰色預測模型是對“小樣本、貧信息”的不確定性問題進行預測的一種有效工具，目前很多專家學者已經將灰色預測模型應用到區間數序列預測。文獻[9]將區間數序列的區間中點及半徑分別看作實數序列，分別建立中點序列和半徑序列的預測模型，通過中點和半徑的預測值還原區間數序列的上界和下界，實現區間數序列的預測；在文獻[10]中，區間數表征可修部件的失效率與修復率，構建灰色狀態轉移矩陣，建立基于灰色生滅過程可修部件備件需求預測模型；但以上方法均采用最小二乘法對參數進行估計，基于最小誤差絕對值最小的假設會造成參數與估值的偏離和平均誤差較大的問題，同時以上方法未考慮到區間數的整體性，會對預測的效果造成不良影響。

針對預測模型的以上不足，本文提出一種基于最近數據優先累積法的GM(1，1)指揮控制系統效能評估指標值預測模型。該模型考慮兩參數區間數的整體性，從通過發展系數和灰作用度的實際意義出發，為了解決最小二乘法作為參數估計方法的不足，通過累積法進行參數估計，并結合指揮控制系統動態性的要求，使用新陳代謝思想對模型進行完善。

2 基于區間數的混合型數據統一

2.1 區間數的定義與運算關系

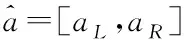
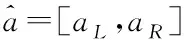
2.2 混合數據統一轉換方法

由于戰場環境復雜，指揮控制系統效能評估的各個指標值來源復雜多樣，導致數據異構，類型復雜。本文提出的方法主要針對指揮控制系統效能評估指標值為實數、區間數、三參數區間數、語言描述和直覺模糊數等四種類型的數據，下面為具體的轉換方法。

1)實數。實數即為精確數，例如指標作戰籌劃效率的指標值為0.87即為一個實數。

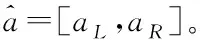
3)語言描述。語言描述是指例如“好、一般、較差”之類的定性描述，對于語言描述r，r∈R，由于r難于使用數值去度量，所以需要語言描述集合才能有對比，進而進行量化。R是一種預先定義好的語言描述集，即R={Ri|i=0，1，…，(T/2)-1，T/2，…，T}，其中Ri表示R中第i+1個語言描述，T為偶數，R中包含T+1個語言描述。例如，當T=6時，此時R={R0，R1，…，R6}，依次對應著“非常差，差，較差，中，較好，好，非常好”這七個語言描述。將語言描述轉換成區間數的公式為：

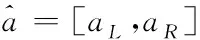
=[max{(i-0.5)/T，0}，min{(i+0.5)/T，1}]

(1)

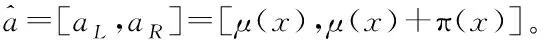
3 基于改進累積法的區間GM(1，1)預測模型

3.1 新陳代謝思想和最近數據優先累積法

3.1.1 新陳代謝思想

新陳代謝原指機體與環境之間的物質和能量交換以及生物體內物質和能量的自我更新過程[13]，現將其運用到效能評估指標值的預測過程中。指揮控制系統作為一個動態系統，在預測了從現在時刻起往后的多個時刻指標值的同時，又產生了新的數據，為了提高效能評估指標值的中長期預測精度，引入新陳代謝思想，將新的數據x(0)(n+1)置入序列，同時剔除數據x(0)(1)，再用序列X(0)={x(0)(2)，x(0)(3)，…，x(0)(n+1)}建立模型，對其進行預測，實現預測結果的實時更新。

3.1.2 最近數據優先累積法

在信息化戰場的大背景下，戰場數據瞬息萬變，新產生的數據比舊的數據對戰場走勢的預測更為重要，應該有著更高的權重，但從傳統累積法存在越早的數據累加次數越多的情況，也就是意味著給陳舊的數據賦予了更高的權重，這有悖于實際情況，從而提出最近數據優先累積法，給新產生的數據賦予更高的權重。

設原始序列為X={x(1)，x(2)，…，x(n)}，定義各階最近數據優先累積和為[14]

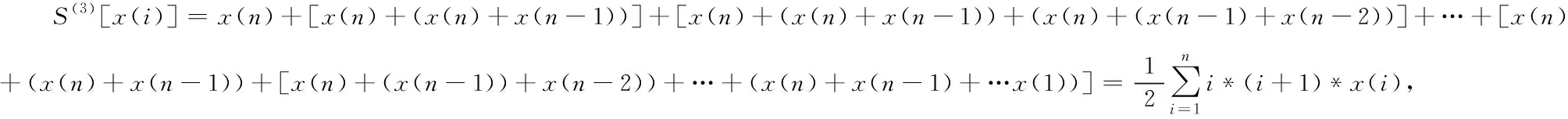
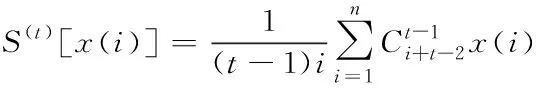
(2)

稱為t階最近數據優先累積和。

特殊地，對于長度為n的全1序列，稱為S(t)[1]為t階最近數據優先累積和，其計算式為

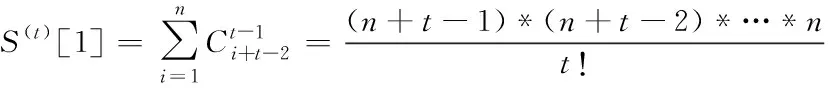
(3)

3.2 基于改進累積法的GM(1，1)預測模型的建模步驟

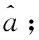
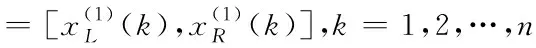
(4)

2)由區間數的一次累加生成序列計算鄰值生成序列，得到白化背景值

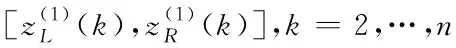
(5)

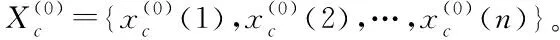
(6)

由式(2)對中點序列的定義型方程(6)兩邊作一階、二階最近數據優先累積和，得

由式(2)，代入相關變量，得一階、二階最近數據優先累積法方程組

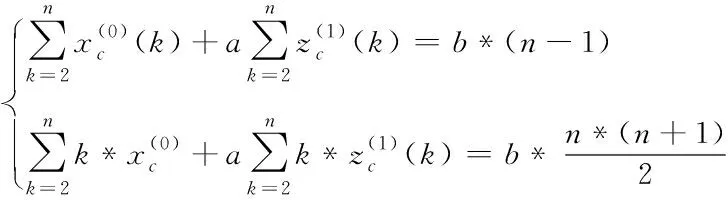
(7)

如果記a=(a，b)T

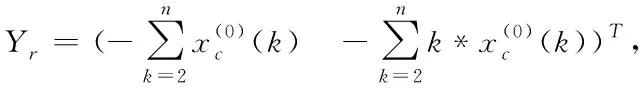
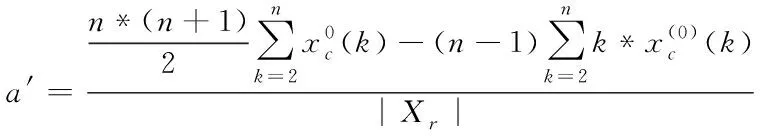
(8)

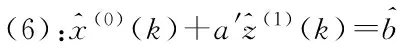
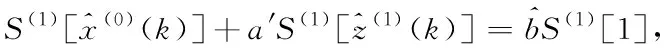
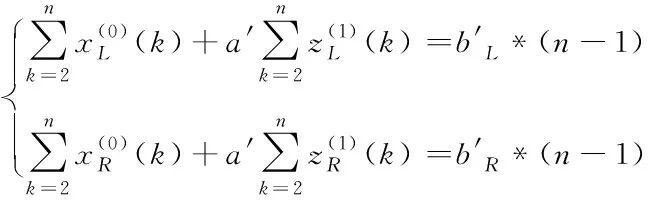
(9)

由式(9)化簡得到

(10)

5)根據文獻[15]中為改進借用白化響應式來表示灰度響應式對結果造成誤差的情況，推導出GM(1，1)模型預測的內涵型公式為

(11)

得出預測結果序列為

6)模型預測的誤差計算和預測精度的計算。區間數的相對誤差計算公式為

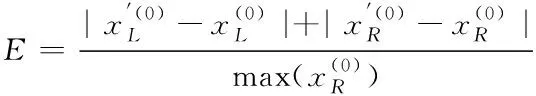
(12)

指標值的預測平均相對誤差是指指標在多個時刻的相對誤差的均值，公式為：

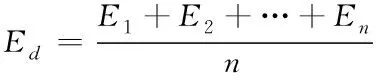
(13)

式中，Ei為指標值在i時刻的預測相對誤差，n為總時刻數。

7)利用新陳代謝思想對預測序列進行更新，實現預測的動態性。

4 實例分析

指揮控制系統是指采用以計算機為核心的技術設備與指揮人員相結合、對部隊和武器實施指揮與控制的“人-機”相融合、實現“全域實時動態”的高效指揮系統。效能評估是對完成作戰任務能力的度量，指標體系是效能評估的關鍵，在結合課題組研究成果和現階段指揮控制系統發展特點與部隊實際，構建了指揮控制系統效能評估指標體系，如圖2所示。

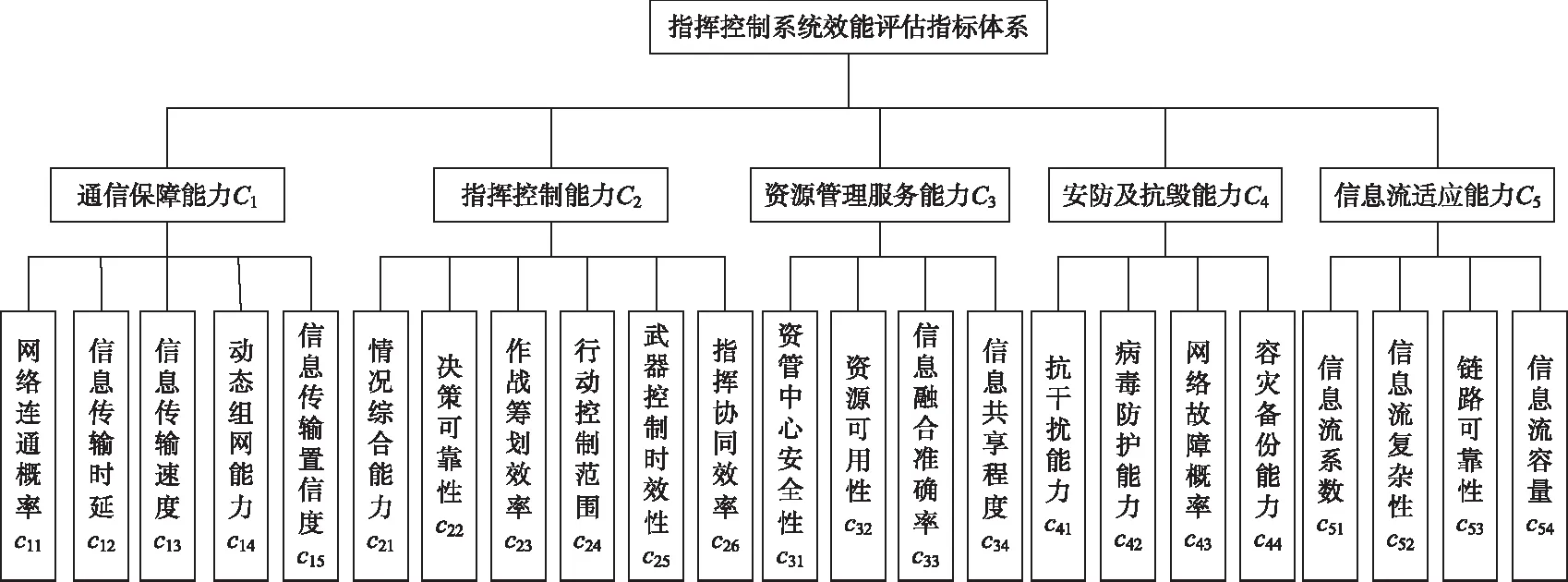
圖2 指揮控制系統效能評估指標體系

本實例以某部隊裝備試驗過程中間隔1小時的12個連續時刻指揮控制系統效能評估指標值為例，運用本文提出的基于新數據優先累積法的區間數GM(1，1)預測模型進行指標值預測的實例分析。由于篇幅受限，計算過程以通信保障能力C1的評估數據為例，其指標包括c11網絡連通概率、c12信息傳輸時延(單位毫秒)、c13信息傳輸速度(光纜傳輸，最大速率155Mb/s)、c14動態組網能力和c15信息傳輸置信度，其中c11、c12、c13和c15為定量指標，指標c11用區間數表示，指標c12用三參數區間數表示，指標c13和c15分別用精確數和直覺模糊數表示，c14為定性指標，用7級語義變量(很差，差，較差，一般，較好，好，很好)表示，指標初始數據信息如表1所示。

使用第2.2節基于區間數的混合型數據統一方法將指標初始數據信息進行統一，其結果如表1所示，其中c1i行表示指標c1i的原始值，c1i′行表示指標c1i原始值轉換后的值。

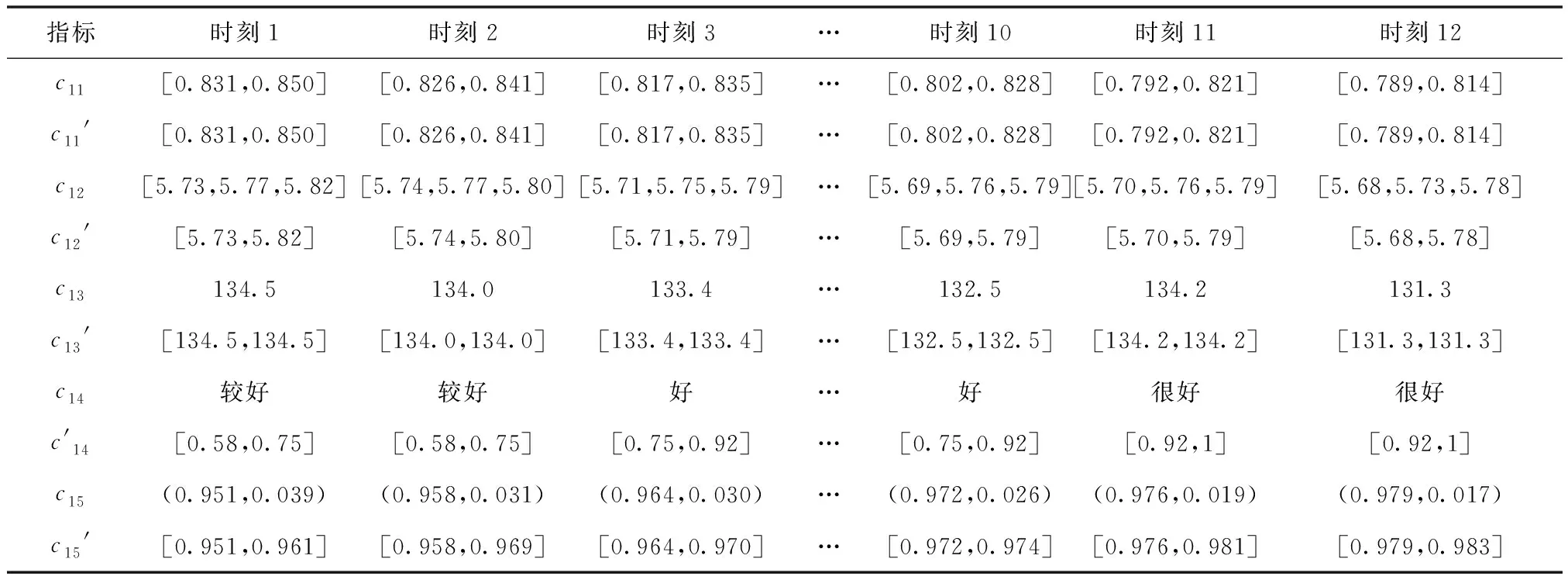
表1 指標數據信息統一后結果

為了驗證本文所提方法的有效性，對前10個指標值數據進行擬合建模，將第11和12個數據用于模型的預測效果分析。以指標c11為例，預測步驟如下：

原始數據序列為

{[0.831，0.850]，[0.826，0.841]，…，[0.802，0.828]}；

1)由式(4)，對原始序列做一次累加生成，得

{[0.831，0.850]，[1.657，1.961]，…，[8.136，8.350]}；

2)由式(5)，生成白化背景值序列，得

{[1.244，1.2710]，[2.066，2.109]，…，[7.344，7.530]}；

3)由中點公式計算得出中點序列，得

{0.841，0.834，…，0.802}；

4)由式(8)和(10)，計算得出發展系數a和灰作用度b的估值分別為

a′=0.0103，′=[b′L，b′R]=[0.8346，0.8579]

5)由式(11)得到

{[0.813，0.850]，[0.822，0.845]，…，[0.797，0.819]，[0.789，0.811]};

以此類推，指標c11-c15應用拓展基于累積法GM(1，1)預測模型對指標值進行預測的結果如表2所示。

6)根據式(12)，計算出相對誤差并填入表2。

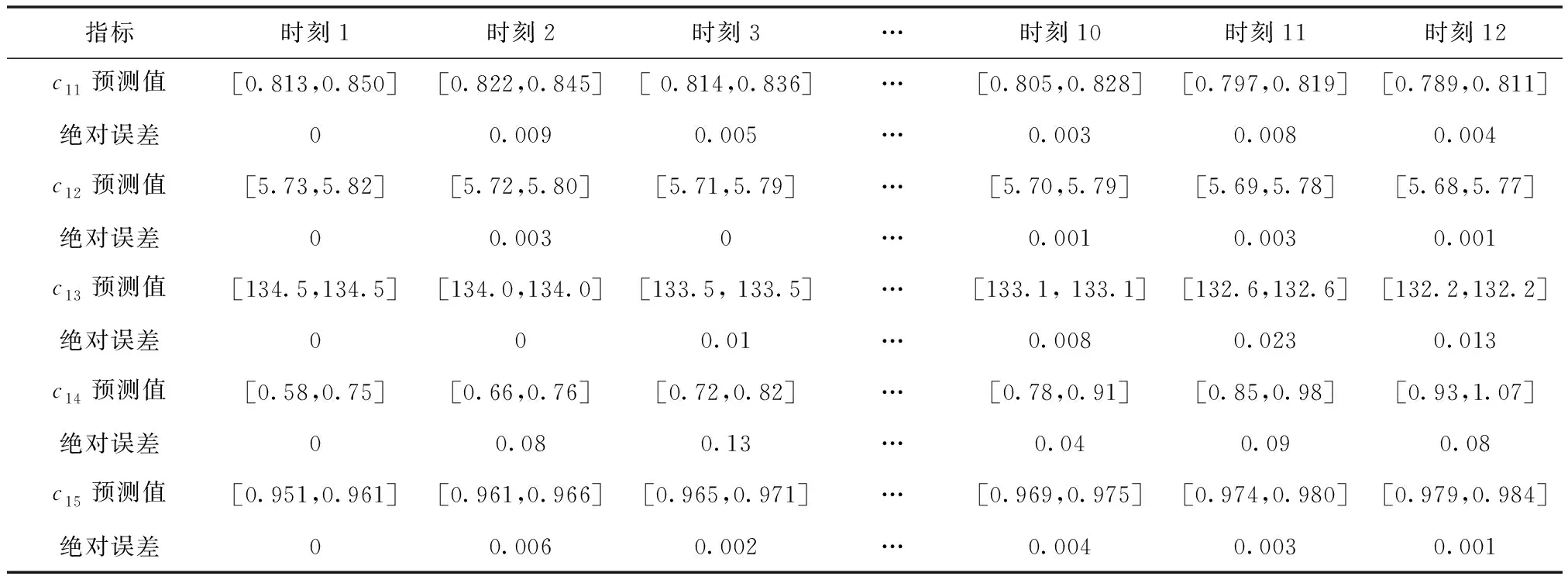
表2 指標數據信息預測結果及相對誤差

根據式(13)，得到各指標平均絕對誤差為：Ec1={Ec11，Ec12，…，Ec15}={0.005，0.002，0.017，0.084，0.004}。

7)當各指標時刻13的指標值采集到了以后，把各指標在時刻1的指標值拋棄，使用時刻2到時刻13的指標值進行新一輪的指標值預測，且可將指標的預測值用于指揮控制系統預測性效能評估，滿足指揮控制系統效能評估的動態性要求。

使用文獻[9]基于中點與半徑的區間數預測方法對本實例的指標值進行預測，預測結果如表3所示。

表3 文獻[9]方法對指標在時刻11和12的預測結果

根據表2和表3的數據、平均絕對誤差和對比文獻[9]的方法，分析可知：c11網絡連通概率隨著時間推移逐漸變小，可能是由于戰損的原因，網絡節點被破壞，網絡連通概率降低，而c13信息傳輸速度在逐漸變小的趨勢在時刻10突然變大，可能是由于連通節點被搶修成功或作戰距離拉近的緣故；從預測結果的平均絕對誤差來看，指標c13和指標c14的誤差較大，指標c13是由于在時刻10的跳變，導致序列趨勢性不明顯和波動較大，從而對預測精度造成了比較大的影響；指標c14是定性指標，在轉化成區間數的過程是一個離散到連續的過程，轉化后數據間跳躍性比較大，導致預測結果的誤差比較大。對比文獻[9]的在時刻11和12的預測結果，可以發現，本文方法除了指標c13的預測結果不如文獻[9]的方法以外，其余指標的預測精度均優于文獻[9]的方法，原因是指標在時刻10的指標值突然變化，導致趨勢發生變化，從而在指標的預測精度上優于本文方法。

依次將一級指標指揮控制能力C2、資源管理服務能力C3、安防及抗毀能力C4和信息流適用能力C5等下的所以二級指標cij分別運用基于新數據優先累積法的區間數GM(1，1)預測模型和文獻[9]的模型進行指標值預測，得出的各指標平均絕對誤差如表4。

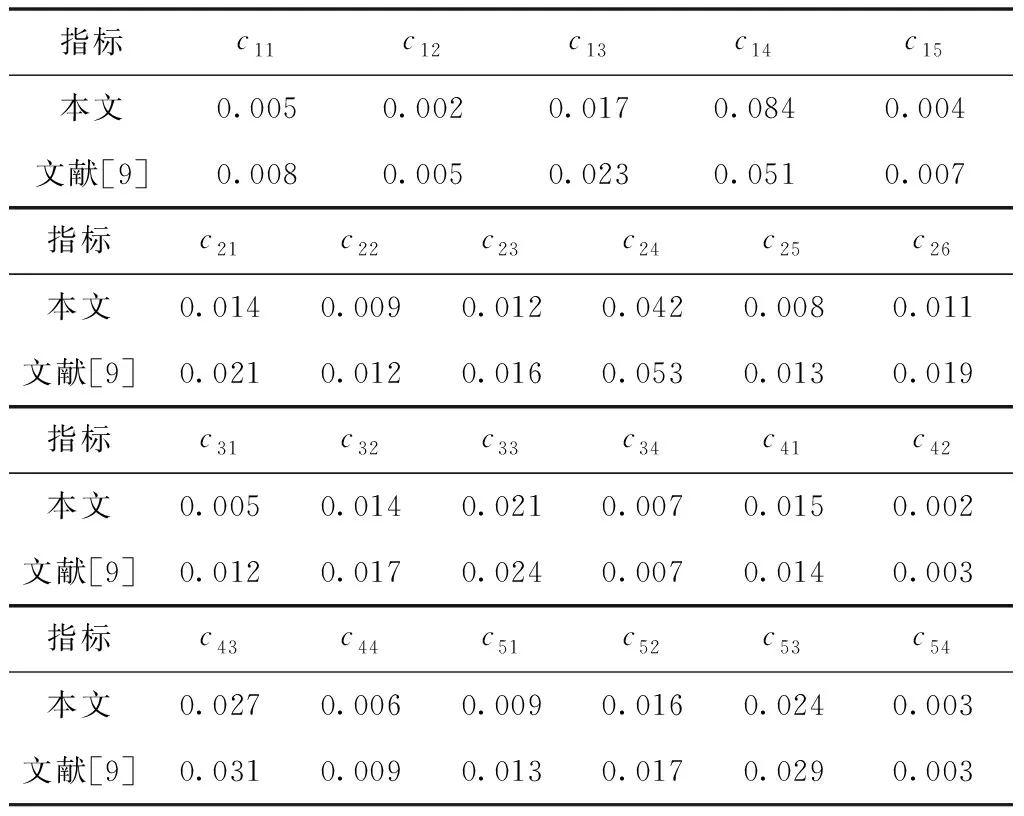
表4 運用本文方法和文獻[9]方法的各指標值預測平均絕對誤差

從表4的預測相對誤差的結果發現，基于新數據優先累積法的區間數GM(1，1)預測模型的預測誤差比較小，預測效果佳，對比文獻[9]中的區間數經典方法，預測誤差普遍比其小，體現了本文方法的有效性。

5 結束語

首先分析指揮控制系統效能評估指標值的特點，將混合類型的數據均轉化成區間數，便于數據的處理；分析了傳統GM(1，1)預測模型使用最小二乘法進行參數估計的不足，最后采用不進行假設的累積法進行參數估計，并對普通累積法的累加順序進行調整，以適應新時刻數據比舊數據對預測更重要的原則，同時改進GM(1，1)預測模型將其預測序列類型從精確數序列預測拓展到區間數序列，再結合新陳代謝思想對預測模型的動態性進行完善。通過指標數據預測實例和與其它區間數序列預測方法進行比較驗證了該模型的有效性。可將預測的指標值結果用于指揮控制系統效能評估中，實現對未來時刻的效能進行預測性評估，增加戰場應對突發事件的反應時間，提高打贏戰爭的能力。