基于Deform的航空發動機葉片金屬鍛造仿真

肖智海，熊 俊，姚志文

(南昌航空大學工程訓練中心，江西 南昌 330063)

1 引言

葉片屬于航空發動機的關鍵零件，承受著多種復雜應力，因此必須具備良好的抗拉性、疲勞強度與耐腐蝕性。通常情況下，葉片型面為復雜的自由曲面，其金屬材料制作難度較大，生產周期很長。鍛造技術可以改善零件組織結構，提高力學性能，廣泛應用在葉片材料制造中。文獻[1]提出基于田口方法的鍛造過程仿真與工藝優化。將田口方法、數值模擬與澆注實驗相結合，分析澆注溫度、鑄型溫度以及涂料厚度對鎖孔體積率造成的影響，并對鍛造工藝進行優化，通過仿真獲得最佳工藝方案。文獻[2]提出基于振動技術的金屬鍛造成型應用研究。對振動形式與設備進行分類，分析金屬液的振動處理、振動充型與振動凝固技術的應用；研究鍛造過程中機械振動和超聲波振動對鑄件微觀組織的改變，得出影響靜力力學性能優化的影響因素，總結不同振動工藝參數對鍛造性能影響規律。

上述鍛造方法雖然縮短了生產周期，但是鍛造后工件完整度低，材料利用率不高。為改善這一缺陷，本文利用Deform軟件實現航空發動機葉片金屬材料鍛造。Deform屬于一套基于有限元分析的仿真系統軟件[3]，通常用于研究金屬成形有關的成形工藝與熱處理技術。其中前處理器可以處理模具與材料信息，構建邊界條件；有限元模擬器是集彈性、彈塑性、熱傳遞于一體的有限元求解器；后處理器可將仿真結果可視化，輸出需要的模擬數據信息。在計算機上對鍛造成型過程、材料內部微觀變化以及交互作用規律進行計算與預測，促進工業技術逐步發展。

2 鍛造工藝模型組織形式研究

2.1 鍛造過程狀態劃分

在分析葉片零件制造狀態和功能基礎上，建立科學的狀態模型[4]是金屬材料鍛造重點。狀態模型一般包含模型數量確定、模型信息內容定義與有效性檢驗三個方面。

1)狀態模型數量確定是指結合工件設計模型，將制作技術與約束條件當作依據，針對工藝設計需求，明確制造狀態數量與功能，確定狀態劃分方法，構建信息組織架構。

2)狀態模型信息內容定義是指將劃分方案與工件設計模型分別當作指導與基本數據，明確定義流程與幾何信息定義方法。將其應用在葉片鍛造多態模型中，形成不同狀態模型下的幾何信息。

3)有效性檢驗表示檢測已經完成模型的有效性，例如能否滿足成形技術要求、是否可以精確展示工件制造程序。

發動機葉片金屬材料鍛造過程中包含多個工序，其中任意一個工序又對應不同制造狀態。根據上述狀態劃分方法，將成形過程分為以下四種狀態演化過程。

毛坯態：結合設計模型尺寸大小、體積等參數，綜合考慮工藝要求挑選棒料毛坯。

中間態：毛坯不能經過一次鍛造就達到成形需要，因此必須經過多個中間工序進行過渡。

成形態：經過一些工序過渡后，已經確定模型結構，再通過切邊、矯正等處理后即可得到成品工件形狀。

多模態設計過程實質上是對鍛造程序的逆序推導。在此過程中鍛造模型結構經歷了從復雜到簡單的蛻變。全部鍛造數據在不同層面之間相互傳遞。不同層面間都是相互關聯的，而這些關聯整體構成了模型結構。

2.2 狀態信息組織原則

葉片金屬材料鍛造模型中的信息來自不同制造工序，例如工序設計、加工過程等。任何狀態下都包括工藝、技術說明等信息。信息種類不同導致儲存結構存在較大差異。

工件制造過程被劃分為不同狀態，每個狀態的需求和功能盡管有所差別，但是信息內容存在相似性。為Deform軟件管理方便，建立以下信息組織原則：

1)構建以零件生產模型為根節點的結構樹[5]，并創造狀態子節點；

2)全部鍛造數據都和狀態版本有關；

3)不同狀態子節點之間不能出現冗余數據。

通過上述原則，利用多態組織生產模型，將工件數據以節點形式組織起來，建立生產模型結構樹，有助于對鍛造不同階段數據進行綜合管理。

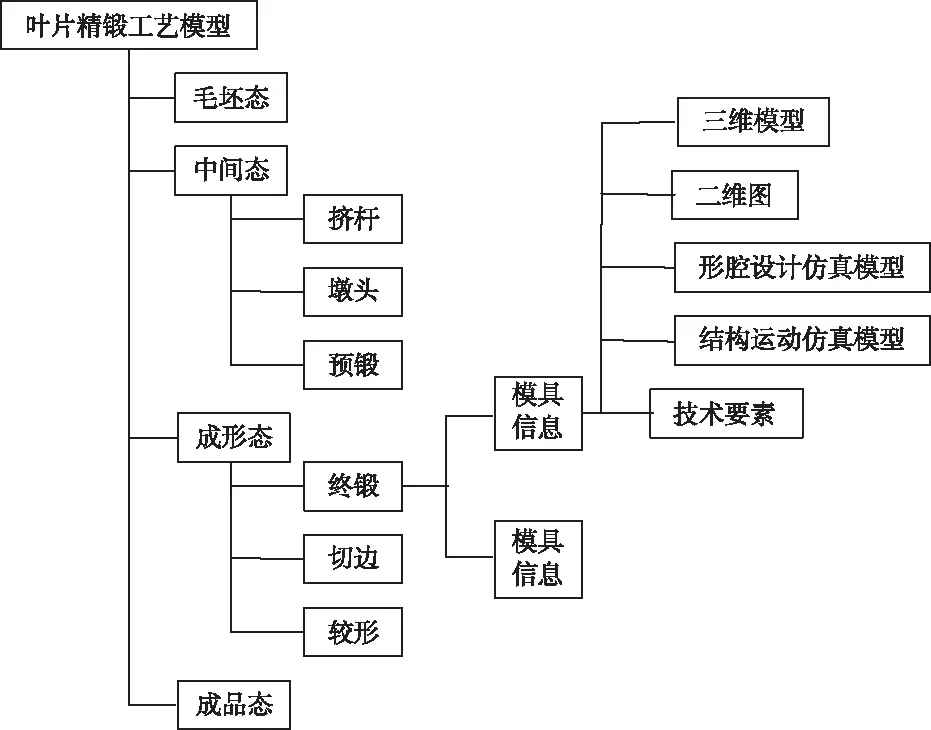
圖1 葉片金屬材料鍛造工藝模型組織形式

3 基于Deform的航空發動機葉片金屬材料鍛造

3.1 影響鍛造的主要因素

1)刮板對鍛造工藝影響

鍛件制坯能夠為鍛造成形制定合理坯料形狀與尺寸，使金屬材料布滿終鍛膜膛，減輕磨損現象，延長使用壽命。因為刮板截面很多，變化明顯，若將其直接用于鍛造，會出現折疊、部分填充不足等缺陷。

2)溫度對鍛造成形影響

溫度是影響塑性與變形的關鍵因素，對鍛造過程中組織形態影響很大。因為發動機葉片屬于大型模鍛件，因此溫度分布不均會影響金屬塑性流動，出現較多鍛造缺陷。

經驗表明，很多因素會對溫度控制產生影響。例如加熱爐溫度、工件和環境溫度之間的傳導等。這會導致鍛件在發生形狀變化，在組織形態上產生不均勻結晶，導致敏感性開裂、組織性能不均勻等問題。所以對溫度的持續監測對鍛造工藝而言十分必要。

3.2 目標函數與設計變量選取

1)鍛件均勻性描述

在判斷鍛件整體變形均勻性時通常利用下述指標

(1)

(2)

由式(1)和(2)能夠得出，在表示鍛件變形均勻性時，僅分析了各部分等效應變極大值和極小值。但實際鍛造過程中，如果等效應數值相同，但分布情況不一致時，變形均勻性[6]也隨之不同。所以，本文在上述基礎上提出如下評價鍛件變形均勻性指標

(3)

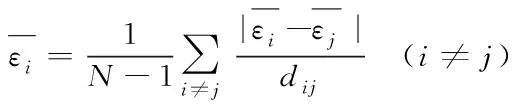
(4)

(5)

對3×3單位距離的矩形求解域[7]進行分析，如果域內僅存在一個單元的應變值是1，其它應變值都是0，則結合其具有的對稱特性，將整體應變分布狀況可分為三種，分別記做ε11=1，ε11=1以及ε11=1。

從表1中能夠看出，針對三種應變分布方式，式(1)和式(2)計算得出的變形均勻性指標值都相同，而本文改進的方法可以清楚表示不同分布狀況的變形均勻性。三種狀況相對的均勻性指標值關系描述為ε22>ε12>ε11，表明應變值為1的單元方位與求解域中心越靠近，其指標值越高，變形均勻性越差。

表1 鍛件變形均勻性指標值表

2)目標函數

在對多目標優化問題進行求解時，線性加權法是較為簡單的方法之一。針對存在兩個目標時，其目標函數可描述為

f=ρ1f1+ρ2f2

(6)

式中，f1與f2分別表示鍛件變形較為均勻與模具填充情況的目標函數，本文對其取值為0.7與0.3，這是因為：僅將確保鍛件完整性與僅提高變形均勻性為目標，所獲得的形狀是沖突的；在滿足葉片金屬材料完整性要求下最大程度提高其變形均勻性；在實際鍛造過程中，得到完整鍛件比改善變形均勻性更容易實現。

根據上述分析，f2的計算公式為

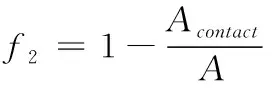
(7)

式中，A表示模具腔總體表面積，Acontact代表工件和模具接觸區域面積。

3)設計變量

將預成形葉片坯料根據最終葉片形狀劃分為多個簡單區域[8]，利用簡單幾何形狀對這些區域進行表述。將鍛件截面大致分為三部分，其中第一和第三部分表示為矩形，其長寬表示幾何參數，記做a1、h1與a3、h3；第二部分屬于過渡區域，利用梯形表示，其上、下底長度為幾何參數，記做h1、h3，高度表示為a2。綜上所述，預成形葉片形狀可通過簡單的幾何參數進行表達，其體積計算公式如下

V=V1+V2+V3

(8)

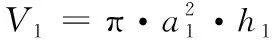
(9)

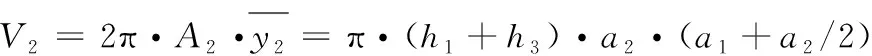
(10)

(11)

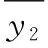
挑選設計變量a，b，c，d和以上預成形幾何參數的關系可表示為

a=V1/V

(12)

b=a1

(13)

c=h3

(14)

d=V3/(V-V1)

(15)

此外，為在鍛造過程中利用第一部分定位，必須確保該部分體積足夠大。

因此，本文利用Deform軟件對葉片金屬材料鍛造預成形設計變量范圍[9]定義在

(16)

3.3 鍛造工藝參數確定

1)材料參數

航空發動機葉片通常將合金、不銹鋼等作為制作材料，本文利用高壓鈦合金葉片，為國產TC4材料。材料數據庫中包括應變曲線、松柏比、輻射率等性能參數。

2)變形溫度

為使TC4鈦合金材料得到較好力學性能，更加符合葉片抗高溫、耐腐蝕等特性，此種材料通常在(α+β)兩個相區之間進行鍛造，加熱溫度需要結合鈦金β相變點來設置，通過測定，β的相變點為990℃。因此坯料加熱理想溫度為940℃，上、下模具溫度控制在200℃左右。

3)網格劃分

在對網格數量進行劃分時需要結合坯料尺寸大小，尺寸越大，劃分數量越多，計算結果也越精確。本文利用四面體網格劃分方法，葉片長度與寬度分別為200mm與80mm，葉片最小特征尺寸為1mm。結合上述信息，將坯料網格總數設置在10到20萬之間。經過對相同坯料分割不同網格數做模擬計算，確保最后劃分的小網格尺寸在0.6～0.9mm之間。這樣即可準確體現出大部分葉片不同區域特性。

4)變形速度

航天發動機葉片鍛造主要利用螺旋壓力機鍛壓，速度控制更加精確。本文將下行速度區間設置在0.5～10m/s，變形速度區間為2～12m/s。根據生產實際狀況，將上模當作主運動模具，運動速度為3m/s。

5)邊界條件

在鍛造過程中利用石墨潤滑劑起到潤滑作用，其摩擦因子為0.1，成形方法屬于熱成形。假設鍛造停止條件是上、下模具閉合高度為150mm，為確保最小網格在全部下壓過程中出現塑性變形，則取最小網格的三分之一當作邊界條件[10]。

圖2 Deform軟件子程序示意圖

3.4 鍛造過程

在整個鍛造過程中，毛坯不但出現變形現象且和下模發生熱傳導作用，為使鍛造效果達到最佳，設置五次熱傳導與五次錘擊。在錘擊時只需要設置第一次變形的邊界條件。則完整的鍛造過程為：

1)工件和下模熱傳遞過程，停止時間為2s。模擬步數是8，模擬步長確定為“With Time Increment”形式；

2)進行第一次錘擊操作，模擬步數是50，模擬步長確定為“With Time Displacement”形式。此時有效錘擊力可達到80%；

3)工件和下模發生熱傳導。移動上模，并進行初始化，持續1s熱交換；

4)進行第二次錘擊，和2)操作相同；

5)重復步驟二與步驟三，直到第5次錘擊結束，即可完成全部鍛造過程。

上述任意一步完成后，可形成數據庫文件，Deform軟件可對這些文件進行自動求解。

圖3 鍛造加工過程流程圖

4 仿真數據分析與研究

為驗證基于Deform的葉片金屬材料鍛造的可行性，進行仿真。利用UG NX6.0軟件實現工件與模具的幾何造型建模，并將其輸出為Deform軟件支持的格式。本次仿真的模具材料是熱作模具鋼4Cr5MoSiV1，將模具加熱到90°，工件取出的原始溫度為1000℃。

鍛件變形均勻程度會影響晶粒尺寸均勻情況，所以必須滿足均勻需求。以1000℃及1300℃的鍛造溫度為例，得到溫度與變形均勻性系數影響關系如圖4所示。

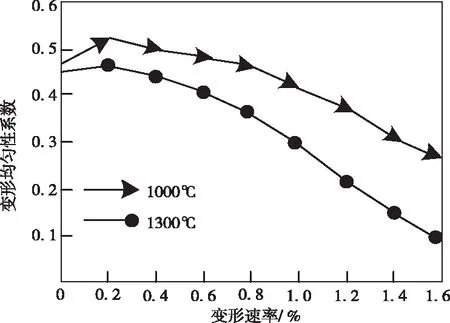
圖4 溫度與變形均勻性系數影響

從圖4中可以看出，在1000℃下，隨著應變速率的增加，鍛件變形均勻性系數逐漸降低，表明鍛件的變形程度越均勻；當溫度升至1300℃時，鍛件的變形均勻性系數明顯降低，同時隨應變速率的增加，鍛件變形均勻性系數逐漸降低。實驗結果表明，鍛件的變形程度隨著溫度的升高及應變速率的增加變得越來越均勻，滿足鍛造要求。

在實際工藝設計中必須考慮鍛造后工件完整程度，將本文方法與文獻[1]、文獻[2]方法進行對比。利用不同方法隨機選出鍛件對比其完整程度，對比結果如圖5所示。

圖5 不同方法鍛造工件完整度對比圖

從圖5中可以看出，本文鍛造方法獲得的最終鍛件完整度高，而其它兩種方法邊緣部分出現不同程度缺失現象，這是因為所提方法設置了準確邊界條件，提高工件完整度。

在此基礎上對材料利用效率進行比較。對比結果分別如圖6所示。

圖6 不同方法鍛造材料利用率對比圖

分析圖6可以看出，在經過多次試驗后，三種方法對于鍛造材料的使用率均保持穩定，其中文獻[1]方法的鍛造材料利用率平均值為71%，文獻[2]方法的鍛造材料利用率平均值為64%，本文方法的鍛造材料利用率平均值為91%，本文方法利用率始終高于其它方法，這是由于該方法使用Deform軟件設計變量，精準控制材料使用情況。

5 結論

對于航空發動機葉片鍛造技術的特殊性，本文在Deform軟件基礎上實現葉片金屬材料鍛造仿真。結果表明，該方法可以滿足鍛件變形均勻性要求，且提高鍛件完整度與材料使用效率，進而降低生產成本，增強企業市場競爭力。在今后研究中可實現鍛造過程向智能制造技術改變，需進一步開發工藝設計與優化專家系統，真正意義上實現航空發動機葉片智能制造。