某轎車側風作用下的氣動特性分析與改進研究

陸潤明，廖抒華，覃紫瑩

(廣西科技大學機械與交通工程學院，廣西柳州 545006)

1 引言

在汽車實際行駛中，氣流是不會總是與汽車的縱對稱面平行的，當氣流與汽車存在橫偏角時，汽車都會產生氣動側力[1]。汽車在有側風的環境下行駛，會受到側向力、側傾力矩和橫擺力矩的作用，其行駛穩定性就會受到影響，會威脅到汽車的行駛安全。在如今，汽車追求低能耗的大背景下，汽車輕量化作為降低能耗的重要手段，但汽車輕量化的同時，會使得汽車的側風穩定性變差，高速行駛時會使潛在的危險性加劇。所以，在新車型開發中，應重視汽車的側風穩定性的研究，降低汽車的側風敏感度，以提高行駛穩定性。

近年來，很多學者在如何提高汽車側向氣動性能上做了研究。如王夫亮等[2]采用穩態方法和動態方法對側風作用下的汽車外流場進行了3種情況的數值模擬，將3種模擬結果進行對比，同時將部分模擬結果與試驗值進行了對比；王露等[3]運用CarSim仿真軟件構建特定道路模型和側風模型，系統地模擬了側風作用下山區高速公路行車穩定性；張英朝等[4]采用橫擺模型法對不同側風下的賽車氣動特性進行了CFD仿真和試驗研究，并對不同側風下流場中速度以及壓力的分布進行了分析，探究了氣動力系數和尾部流場的差異；楊彬[5]對階背式MIRA模型在自然側風下的風阻、壓力場、外流場等表現進行了數值模擬仿真研究。在汽車受側風影響這個方向上的研究，對汽車行駛中側向風帶來的影響研究居多，對汽車側向氣動性能優化的偏少。

本文以某轎車為研究對象，采用與實際行駛情況接近的移動地面穩態模擬方法[2]，分析了在不同強度側風下轎車影響車身周圍流場的變化。運用網格自適應方法、試驗設計、近似模型等技術方法，探討車身兩側表面結構參數對轎車的側向氣動性能的影響，并在此基礎上，優化車身兩側的結構參數，以提高轎車側向氣動性能。

2 計算模型搭建與邊界條件

2.1 建立仿真模型

在車型開發初期，主要考慮車身周圍的流場特性，且不考慮汽車內流場的影響，所以對模型的表面特征進行簡化。幾何處理如下：去除車身最外層表面以外的特征、封閉進氣格柵、封閉輪胎且車身底面用平面覆蓋，處理后的幾何表面如圖1所示。

圖1 處理后的幾何表面

研究表明，只有阻塞比低于1%的風洞實驗結果，阻塞干擾產生的誤差才能被忽略[6]，計算如(1)式

(1)

式中，ε為阻塞比，A為汽車正投影面積，AN為虛擬風洞入口面積。

本次仿真中，建立高為10m，寬20m，長50m的虛擬風洞，如圖2所示。模型正投影面積A：1.951389m2，虛擬風洞入口面積AN：200m2，所以ε=0.98%<1%，滿足阻塞比的要求。

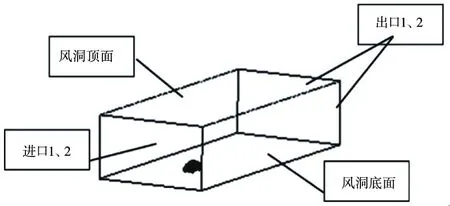
圖2 虛擬風洞示意圖

為更好地捕捉車身周圍的流場現象，在車身周圍設置多個局部網格加密區，以提高車身周圍的計算精度，設置邊界層網格并生成體網格，建立完成的仿真模型如圖3所示。

圖3 對稱面網格截圖

2.2 物理模型的選擇

物理模型的選擇決定于虛擬風洞的氣流流動狀態，氣流流動狀態主要有兩種形式，即層流和湍流。流動狀態的可以由雷諾數的大小得出，計算如(2)式

(2)

當Re?2300，可知其流動狀態屬于高雷諾數湍流狀態。高雷諾數湍流模型一般有以下幾種：標準k-epsilon模型、RNG k-epsilon模型和Realisable k-epsilon模型。而Realisable k-epsilon模型相對于標準k-epsilon模型和RNG k-epsilon模型，其滿足對雷諾應力的約束條件，因此可以在雷諾應力上保持與真實湍流一致。同時文獻[7]對轎車外流場CFD分析中常用k-ε湍流模型做了對比分析和實驗驗證，證明了Realisable k-epsilon模型更適合轎車的氣動性能分析。本文選用Realisable k-epsilon湍流模型，其流動方程表達如下：

湍動能k方程

+Pb-ρε-YM+Sk

(3)

耗散率ε方程

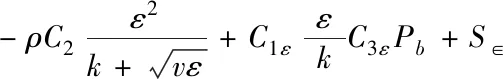
(4)

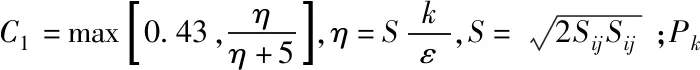
2.3 近壁面處理

在臨近壁面的區域，在壁面的法線方向上速度存在很大的梯度，在很小的距離內速度的變化很大。為保證更準確地模擬在近壁面的流動，需要在黏性底層布置較多的節點，邊界層網格質量可通過控制y+值得范圍來實現，對于高雷諾數模型，y+≈30，進而得出確定邊界層網格與壁面的最小距離y，y由以下(5)-(9)式得出

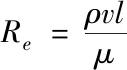
(5)

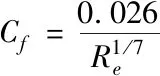
(6)

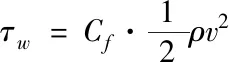
(7)

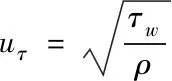
(8)

(9)

式中，Re—雷諾數，ρ—空氣密度，v—氣流平均速度，l—特征長度，μ—動力黏性系數，Cf—壁面摩擦系數，τw—壁面切應力，uτ—壁面摩擦速度。

在本次仿真中，空氣密度1.18415kg · m-3，氣流平均速度120km·h-1，特征長度2.55m，動力黏性系數1.85508×10-5k g ·(m · s-1)，y+取30。代入數據至(5)-(9)式，邊界層中首層網格厚度為3.7×10-4m，所以設置首層網格厚度為0.37mm。

2.4 邊界條件的設定

汽車行駛時周邊氣體流速不高，壓強變化小，所以在研究汽車外部氣流流動時，可以忽略壓縮性的影響[1]。其控制方程如下：

連續方程(質量守恒方程)

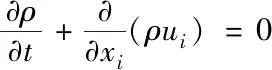
(10)

式中：ρ氣體密度，ui為i方向的速度分量

動量守恒方程

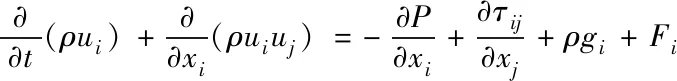
(11)

式中：P是靜壓力，τij是應力矢量，ρgi是i方向的重力分量，Fi是由阻力和能源引起的其它能源項。

氣體狀態方程

PV=ρRT

(12)

式中，P—氣體壓強，V—氣體體積，ρ—氣體密度，R—氣體常數，T—氣體熱力學溫度。

邊界條件設置如表1所示。

表1 仿真分析邊界條件

仿真模擬試驗設置車輛行駛速度恒定為120km/h，橫擺角分別為：0°、5°、10°、15°、20°，速度加載的方式為車輛行駛速度與側向風速的合速度，橫擺角、車輛行駛速度、側向風速、合速度的關系如表2所示，在仿真模擬中的合速度加載方式[8，9]如圖4所示。

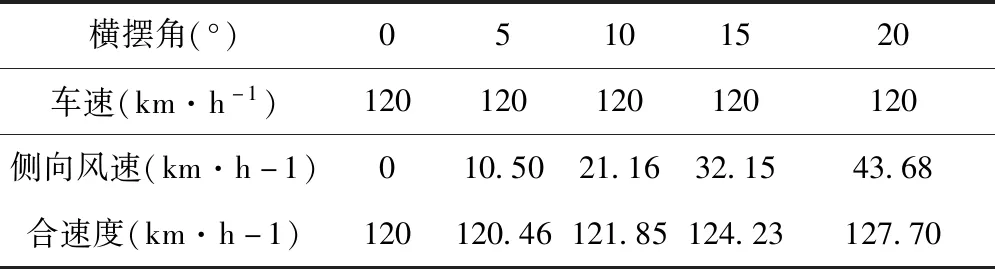
表2 橫擺角、車速、側向風速、合速度的關系

圖4 側風加載方向示意圖

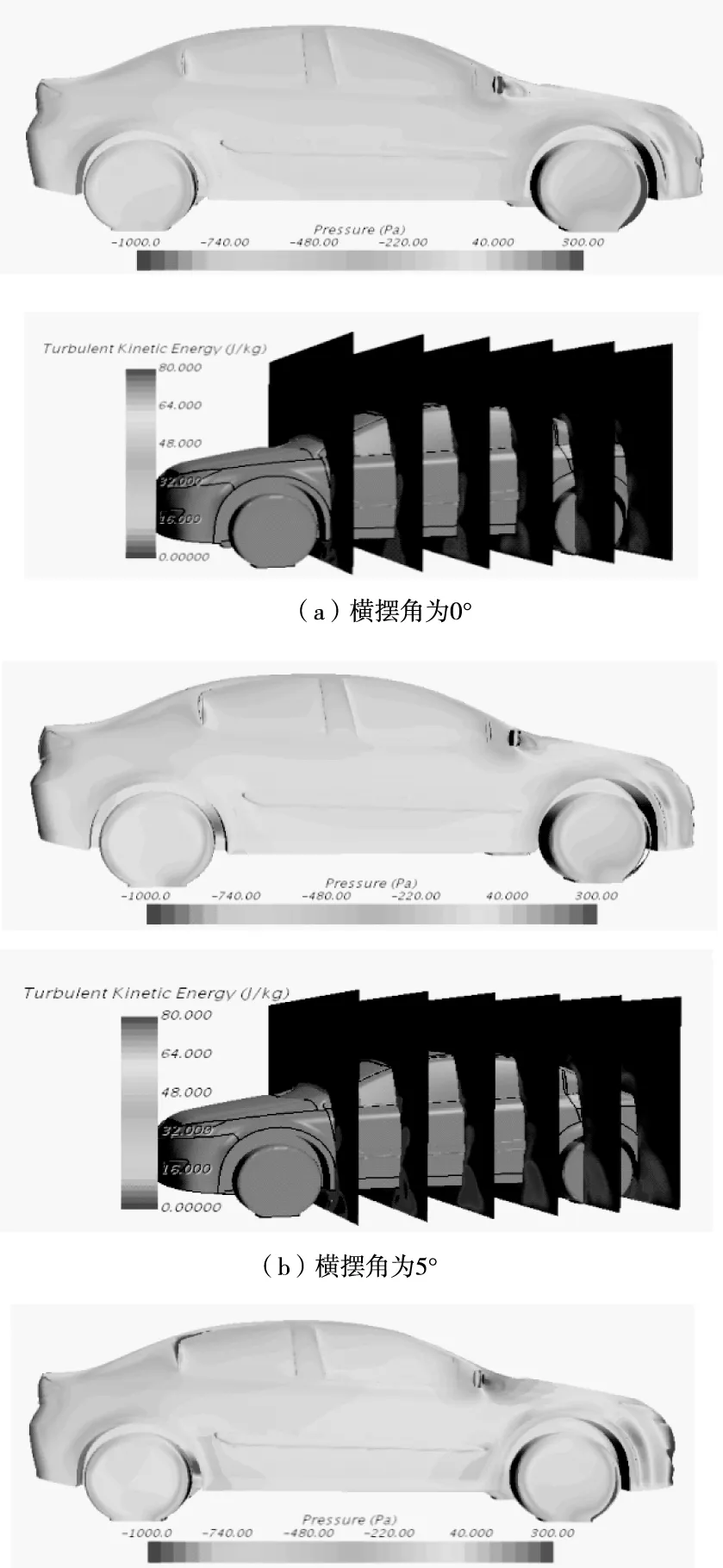
圖5 各橫擺角下車身表面壓力分布及車身兩側流場湍流動能圖

3 不同強度側風下汽車外流場分析

由圖5可以看出，隨著橫擺角的增大，車身迎風側表面壓力也越來越大，在車身背風側面的湍流動能也越來越大，亦即在車身背風側的能量損失越來越大。這樣在車身迎風側表面壓力增大，車身背風側面的壓力減小，導致車身兩側面的壓差隨著橫擺角的增大而增大，且由車身表面壓力分布可以看出，隨著橫擺角的增大，壓力值也在逐漸變大同時，風壓中心逐漸往車頭方向移動。

圖6 橫擺角與氣動側力系數關系圖

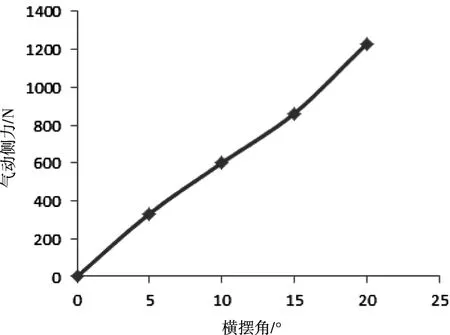
圖7 橫擺角與氣動側力關系圖

由圖6、圖7可以看出，當橫擺角越大，氣動側力系數就越大，氣動側力也越大，且近乎線性增大，當橫擺角為20°時，氣動側力系數為0.847，氣動側力為1231N，約為整車重量的9%。

當汽車受到側力影響時，汽車本身并不能產生力一個平衡力，只能靠駕駛員通過方向盤修正保持方向，但這樣會加重駕駛員的疲勞感和影響汽車的行駛穩定性，威脅行車安全。通過優化汽車外形，降低汽車外形對側風的敏感度，從而降低側向力對行車的影響。

4 優化設計

4.1 試驗設計分析

使用試驗設計方法，可以有效地減少復雜系統仿真次數，提高優化分析效率，幫助辨識關鍵的試驗因子、確定最佳的參數組合、分析輸入參數與輸出參數之間的關系和趨勢、構建經驗公式和近似模型等[10]。本次試驗選用最優拉丁超立方法，此方法能夠使試驗點盡量地均勻地分布在設計空間，具有很好的空間填充性和均衡性。

4.2 參數變量設計

采用FFD(Free Form Deformation)參數化方法對變量實現網格自適應變形，該方法仿照彈性物體受外力后發生相應的變形這一物理現象，將研究對象置于控制體當中，給控制體施加外力，則控制體內的所有幾何發生相應變形，處于其中的研究對象形狀也即發生變化[11]。從文獻[12]可知，車身側面結構對車輛的側向氣動性能有很大的影響。本次優化只調整車身的橫向特征。通過對不同強度側風下汽車外流場的分析，結合氣流分離機理，在不影響車輛裝配要求、使用性能等的前提下，在車身兩側選擇的結構參數變量為：側窗傾角、側圍弧度和門檻弧度，各變量控制點變化如表3所示，在網格變形軟件sculptor中建立對應的參數化模型。本次試驗選用橫擺角為20°的側風條件下進行車身側面結構優化，以氣動側力系數為優化目標，在全局尋求各參數變量的最優組合，參數變量設計如表2所示。

表3 參數變量設計

4.3 試驗設計結果分析

由圖8主效應圖可知，側圍弧度對整車氣動側力系數的影響較大，且與氣動側力系數近乎呈線性關系。如圖9所示，根據線性回歸模型的系數大小判斷各變量對氣動側力系數的貢獻率，由圖可以看出，三個變量與氣動側力系數之間均呈正相關關系。由圖10各變量之間的交互效應圖可知，三個變量兩兩之間的交互作用不明顯，且有相同的趨勢，起相互促進的作用。

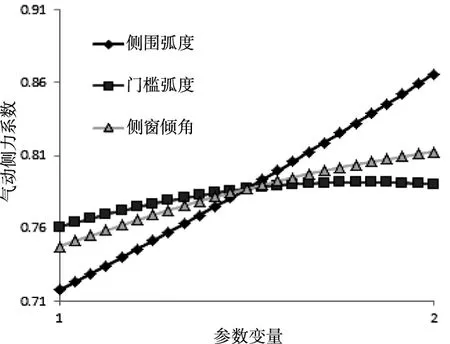
圖8 主效應圖

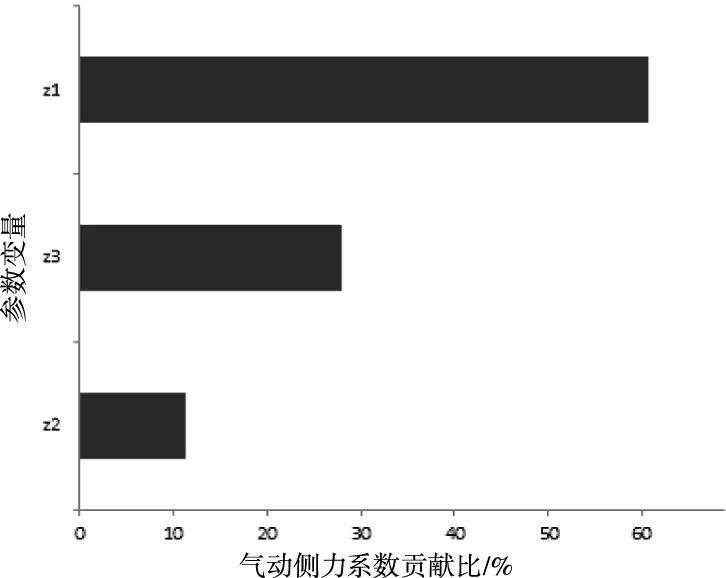
圖9 Pareto圖

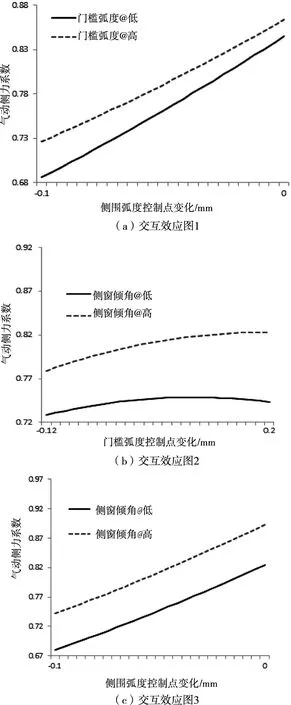
圖10 各變量之間的交互效應圖

4.4 近似模型可信度分析及選擇

近似模型方法(Approximation Models)，通過構建逼近輸入變量和響應變量關系的數學模型，替代仿真軟件高昂的計算代價。這種方法加快了尋優速度，減小了計算量并縮短計算周期。常用的近似模型包括：響應面模型、神經網絡模型、Chebyshev正交多項式模型和Kriging模型。不同的近似模型有不同的特點和優勢，通過比較不同近似模型對樣本點的擬合精度，對各近似模型進行可信度分析，如圖11所示，是擬合精度的散點圖，橫坐標為近似模型預測值，縱坐標為仿真值，斜線是近似模型預測值與仿真值的等值線，由散點圖可知，Kriging模型的擬合精度最好，擬合精度系數R2為0.967，結合文獻[13]的實驗驗證，本次優化選用Kriging模型。

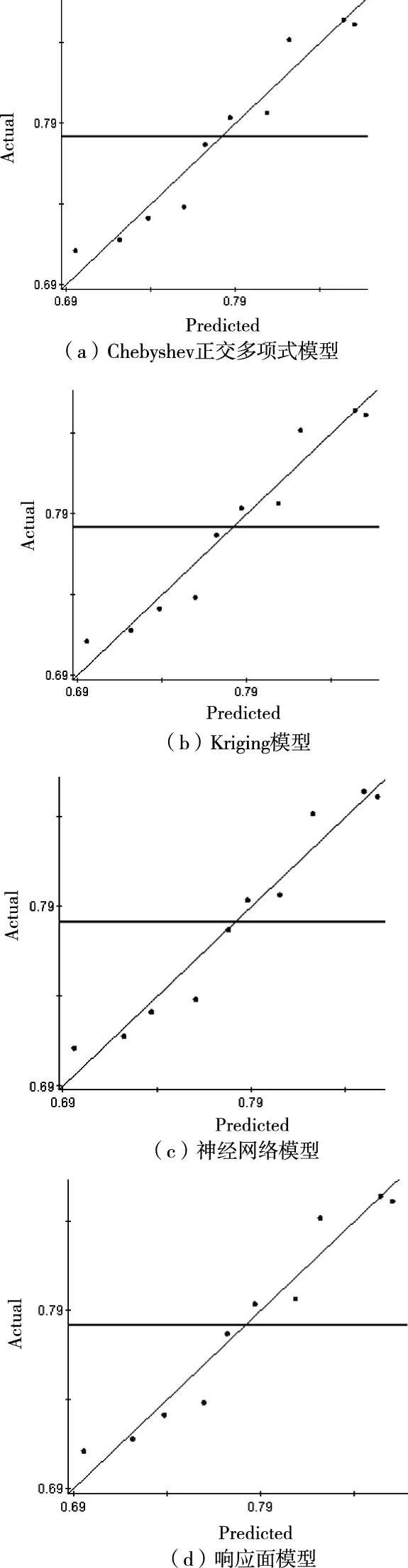
圖11 各近似模型擬合散點圖

4.5 優化方法

本次試驗選用多島遺傳算法(MIGA)在整個設計優化空間進行尋優。這種方法模仿生物進化的遺傳繁殖機制，對優化個體進行編碼，然后對編碼后的個體進行選擇、交叉、變異等遺傳操作，在優化過程中具有很好的魯棒性，故使用該方法在整個優化空間內進行自動尋優。

5 優化結果分析與仿真驗證

通過建立近似模型進行全局尋優，近似模型預測值與對應的控制點變化范圍如下：

表4 控制點變化與預測值

對近似模型的預測結果進行仿真驗證，結果如表5所示

表5 優化結果驗證

近似模型的預測值與仿真值之間誤差值為0.018，誤差較小，即氣動側力系數降低18.65%，對應的氣動側力值減小了230N，優化效果良好。優化前、后車身周圍流場對比如圖。

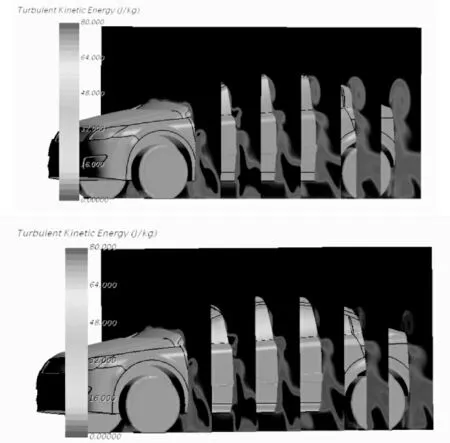
圖12 優化前、后車身兩側湍流動能圖

圖13 優化前、后車身迎風側表面壓力分布

圖14 優化前、后車身背風側表面壓力分布

由圖12為優化前、后的湍流動能圖，由圖可見，優化后車身背風側的湍流動能明顯減小，故在車身背風側的氣流能量耗損降低，亦即車身兩側湍流情況有所改善。

由圖13、圖14可看出，優化后車身迎風面的壓力有所降低，背風側壓力升高，使得車身兩側區域壓力差減小，從而使車輛受到的側向力減小。根據計算可知，原始模型以120km·h-1的速度行駛時，遭遇右側43.68 km·h-1的側風影響時，受到的氣動側力為1231N，在相同環境條件下，優化后模型的氣動側力為1001N，優化后模型的氣動側力降低230N。

6 結束語

文章分析了在車輛以120km·h-1直線行駛，遭遇不同強度側風影響下的車輛外流場的變化，并在橫擺角為20°的側風條件下，探索車身兩側表面結構參數與車輛側向氣動性能的關系，進而優化車身側面結構參數，提高車輛的行駛穩定性。

研究結果表明：

1)在不同強度側風作用下，車身周圍流場都有明顯變化，車身兩側的壓力差隨著側風強度增大而增大，風壓中心隨著側風強度增大而逐漸往車頭方向移動。

2)氣動側力系數和氣動側力都隨著側風強度的增大而增大，且增長趨勢明顯。

3)運用網格自適應方法、試驗設計方法與近似模型方法相結合進行車身側面優化，相比于傳統車身優化方法大幅度減少了優化時間。

4)通過優化車身側面結構：側圍弧度、側窗傾角、門檻弧度，使氣動側力系數降低18.65%，有效地提高車輛在側風作用下的氣動穩定性。