基于局部離群點檢測的高頻數據共現聚類算法
周志洪,馬 進,夏正敏,陳秀真
(1.上海交通大學網絡安全技術研究院,上海 200240;2.上海市信息安全綜合管理技術研究重點實驗室,上海 200240)
1 引言
高頻數據就是大數據的簡化形式。在高頻數據集內存在大量雜亂無章的信息,也存在一些具有規律的信息,準確存儲與分析這些高頻數據可促進經濟發展[1-3]。
離群點檢測屬于數據挖掘的主要方法,離群點檢測負責分析目標數據集,主要找到數據集內異常數據或具有特征的數據信息[4]。葉福蘭研究基于離群點檢測的不確定數據流聚類算法,提升聚類算法的伸縮性[5];趙建龍等研究一種基于仿射傳播的增強型流聚類算法,提升聚類效率[6]。
通過對高頻數據研究發現,當高頻數據中存在相同或類似數據信息時,通常存在很多和數據信息有關的數據標簽同時出現,且出現概率較高,這些數據標簽即為高頻數據共現。針對高頻數據共現,研究基于局部離群點檢測的高頻數據共現聚類算法,提升高頻數據聚類的執行效率與準確性。
2 基于局部離群點檢測的高頻數據共現聚類算法
2.1 局部離群點檢測算法
2.1.1 相關定義
局部離群檢測算法是利用一種模糊方式判斷高頻數據集中是否存在異常高頻數據對象,并對其實施挖掘[7]。
定義1:對象x的k距離。在高頻數據集D內的任意一個正整數k,對象x的k距離由k-distance(x)代表,對象x與對象o(o∈D)間的距離由e(x,o)代表。若k-distance(x)=e(x,o),那么需要符合的條件如下:
1)最少存在k個對象o′∈D/{x},該對象到對象x的距離e(x,o′)≤e(x,o);
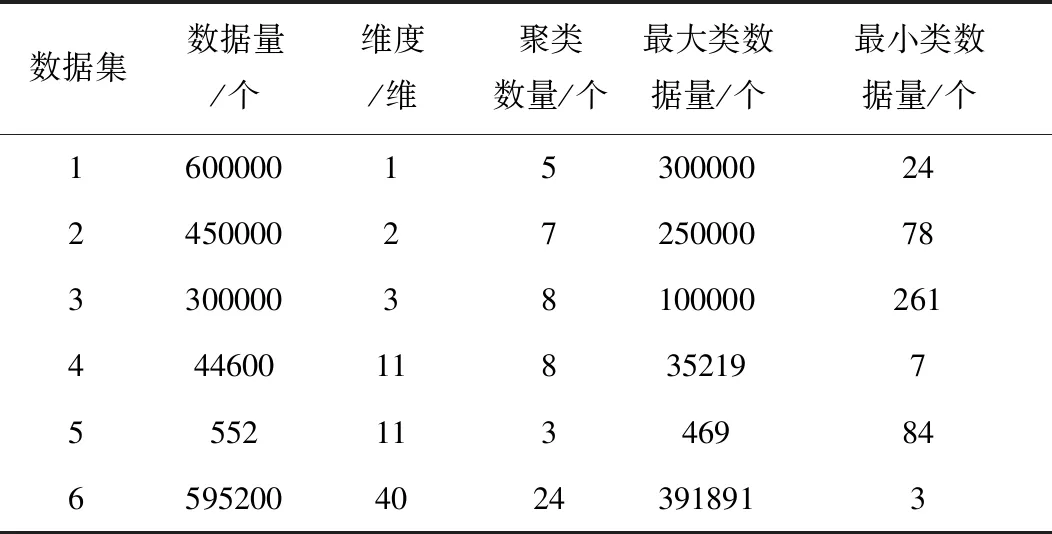
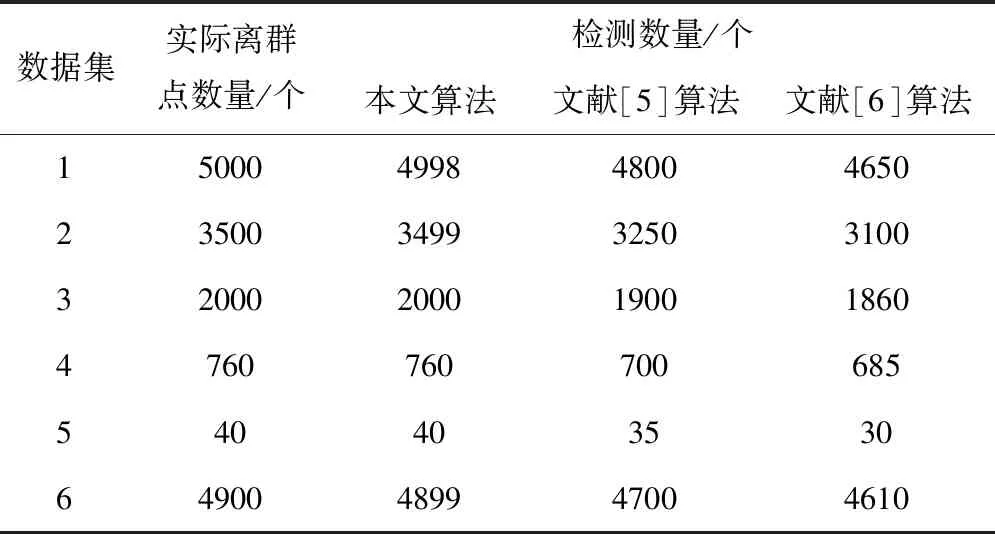
2)最多存在k-1個對象o′∈D/{x},該對象到對象x的距離e(x,o′) 定義2:對象x的k-distance(x)鄰域。對象x的k-distance(x)是已知的,高頻數據集D內的對象y與對象x間的距離小于k-distance(x)的全部對象集合,公式如下 Ndistan ce(x)(x) ={y∈D/{x}|e(x,y)≤k-distance(x)} (1) 定義3:對象x與對象o間的可達距離。假設k屬于一個自然數,定義對象x與對象o間的可達距離公式如下 reach-distk(x,o) =max{k-distance(o),e(x,o)} (2) 根據可達距離定義可知,若x偏離o,那么x與o間的可達距離和x與o間的實際距離一致;若x與o非常接近,那么x與o間的可達距離和o的k-distance(o)一致。 定義4:對象x的局部可達密度。定義對象x的局部可達密度公式如下 (3) 式中,高頻數據集內高頻數據對象的總數是N。根據式(3)可知,x的MinPts個最近鄰居的平均可達距離的倒數是x的局部可達密度。 定義5:對象x的局部離群因子。定義對象x的局部離群因子公式如下 (4) x的離群程度由x的局部離群因子表示。按照式(4)可知,x越偏離MinPts個鄰居以及離群因子越大,那么x的局部可達密度越小以及MinPts個最近鄰居的局部可達密度越大。 局部離群檢測算法的輸入的是高頻數據集D與離群點數目n;輸出的是指定的N個離群點集合。具體執行步驟如下: 步驟1:利用上述公式分別計算已給的高頻數據集內的隨機記錄x的局部離群因子值; 2.1.2 基于可變網格劃分的局部離群點檢測算法 在局部離群點檢測算法中引入可變網格劃分,通過劃分網格空間確定聚類區域,不需浪費時間搜索聚類區域,提升局部離群點檢測算法的執行效率[8]。可變網格劃分方法首先等間距劃分高頻數據空間的各維度,再合并與該維相似的區間段,最后形成網格空間。 步驟2:獲取相鄰區間段的相似性。等間距劃分各維度后,兩個相鄰區間段的相似性εr由這兩個相鄰區間段的全部高頻數據點數量比值代表,其中r=(1,2,…,k-1)。兩個相鄰區間段的相似性εr計算公式如下: (5) 步驟3:按照順序對比第i維內相鄰區間段的相似性εr。若閾值Ti(0≤Ti≤1)小于εr,那么代表這兩個相鄰區間段屬于相似的;若閾值Ti(0≤Ti≤1)大于εr,那么代表這兩個相鄰區間段屬于不相似的;完成對比后,合并相似的區間段。 步驟4:從步驟1到步驟3循環計算高頻數據集各維的相似區間段,并合并相似區間段,輸出網格空間。 2.1.3 設置參數 在構建網格空間過程中,各維度等間隔劃分的區間段數量是k。假設d維度中存在N個高頻數據對象的高頻數據集,按照式(6)設置參數k,可防止網格數量跟隨維度與網格劃分粒度出現提升的情況,參數k設置公式如下 (6) 針對任意維度,其維度上需合并的區間段數量由Ti值確定。若采用一個固定的相似性閾值實施合并操作,便不能準確描繪高頻數據集在空間的分布情況[9]。因此,對于第i維,需按照高頻數據的實際分布狀況決定Ti的取值,參數Ti的取值公式如下 (7) 根據式(7)可知,通過任意維度的全部相鄰區間段相似性的平均值獲取Ti,利用式(7)設置相似性閾值,提升合并區間段的合理性。 2.1.4 算法執行步驟 基于可變網格劃分的局部離群檢測算法輸入的是目標高頻數據集D、密度閾值MinP與離群點數量n;輸出的是前n個比較大的離群因子值對象。具體執行步驟如下: 在實施局部離群點檢測后的高頻數據集中,經常出現不一樣的數據標簽記錄同一個數據集的現象[11]。如果數據標簽t1與數據標簽t2記錄同一個數據集,那么這種情況叫作t1與t2共現。若兩個數據標簽經常記錄同一個數據集,則這兩個數據標簽可能存在相似的語義。利用兩個數據標簽一起標記同一個數據集的次數表示這兩個數據標簽間的相似度。兩個數據標簽記錄同一個數據集次數與這兩個數據標簽的相似度成正比。 數據標簽ta與數據標簽tb的相似度計算公式如下 sim(ta,tb)= (8) 式中,數據標簽ta與數據標簽tb的相似度是sim(ta,tb);數據標簽ta記錄數據集ww的次數是fw,a;通過式(8)能夠計算s個數據標簽兩兩間的相似度,便能獲取數據標簽相似度矩陣Ts×s,Ts×s矩陣內元素的值就是式(8)內的sim(ta,tb)。 數據標簽ta和通過s個數據標簽聚類成的類cs的相似度計算公式如下 (9) 通過式(9)能夠獲取數據標簽和類間的相似度,然后獲取數據標簽和類的相似度矩陣H1,H1矩陣內的元素就是式(9)內的sim(ta,cs)。 通過v個數據標簽聚類形成的類cv與通過s個數據標簽聚類形成的類cs的相似度計算公式如下 (10) 通過式(10)能夠獲取類和類間的相似度,然后獲取類和類的相似度矩陣H2,矩陣內的元素就是式(10)內的sim(cv,cs)。 高頻數據共現聚類算法的基本思想是:對高頻數據集D實施局部離群點檢測挖掘高頻數據對象,計算挖掘后高頻數據對象內數據標簽t間的高頻數據共現相似度sim(ta,cs),再結合層次聚類算法完成高頻數據共現聚類。 為驗證本文算法實施高頻數據共現聚類的執行效率與準確性,以某大學的高頻數據集為實驗對象,從中選取6組高頻數據集,共分為人工數據集與UCI(University of Californialrvine,標準測試數據集)數據集兩種類型,其中數據集1-3屬于人工數據集,數據集4-6屬于UCI標準數據集。通過Matlab工具箱內自帶的函數生成人工數據集;在http:∥archive.ics.uci.edu/ml/內獲取UCI標準數據集。6組數據集的具體信息如表1所示。 表1 6組數據集的信息 利用本文算法與文獻[5]算法、文獻[6]算法檢測6組數據集中離群點數量,文獻[5]算法是基于離群點檢測的不確定數據流聚類算法研究,文獻[6]算法是一種基于仿射傳播的增強型流聚類算法。三種算法的離群點數量檢測結果如表2所示。 表2 三種算法的離群點數量檢測結果 根據表2可知,在不同數據集中,本文算法對6組數據集離群點檢測的數量和實際數量最大差值是2,其余兩種算法檢測的離群點數量與實際數量差距較大。實驗證明:本文算法檢測離群點數量的準確性更高。 利用本文算法與文獻[5]算法、文獻[6]算法對6組數據集實施高頻數據共現聚類,三種算法分別用a、b、c表示,三種算法分別實施3次實驗,避免隨機初始化導致的誤差,執行時間測試結果如表3所示。 表3 三種算法高頻數據共現聚類處理的執行時間 根據表3可知,本文算法與文獻[5]算法、文獻[6]算法相比,本文算法對6組數據集實施3次高頻數據共現聚類處理的執行時間均高于其余兩種算法,原因是本文算法加入可變網格劃分方法可對原始數據集實施一定程度上的約簡,提升高頻數據共現聚類處理的執行效率。實驗證明:本文算法高頻數據共現聚類的執行效率更快。 利用F-measure評價高頻數據共現聚類的準確性,F-measure綜合了準確率P與召回率R。F-measure的計算公式如下 (11) 其中,高頻數據共現聚類是c,類標記是u。 高頻數據共現聚類的總體評價指標F-measure通過加權求和所有聚類結果得到,F-measure值與高頻數據共現聚類效果成正比,即F-measure值越高,聚類準確性越高,L為矩陣行數,計算公式如下 (12) 利用本文算法與與文獻[5]算法、文獻[6]算法對6組高頻數據集實施高頻數據共現聚類,三種算法分別實施3次實驗,避免隨機初始化導致的誤差,三種算法實施高頻數據共現聚類的F-measure值測試結果如表4所示。 表4 三種算法F-measure值測試結果 根據表4可知,對于6組不同數據集本文算法實施高頻數據共現聚類的準確性明顯高于其余兩種算法。實驗證明:本文算法的高頻數據共現聚類效果更好。 為進一步驗證本文算法的準確性,以數據集1為例,測試本文算法與文獻[5]算法、文獻[6]算法在不同k值與top-n作用下高頻數據共現聚類的聚類精度(聚類精度=聚類到的高頻數據共現數量/全部高頻數據共現數量)。三種方法在不同k值作用下高頻數據共現聚類的聚類精度與執行時間分別如圖1與表5所示。 圖1 在不同k值作用下三種方法的聚類精度 根據圖1可知,隨著k值的不斷提升,三種算法的聚類精度均有所提高。在k值為30個時,三種算法的聚類精度均處于最高值,在k值逐漸增加時,本文算法的聚類精度明顯高于其余兩種算法,本文算法的聚類精度變化比較平穩,在k值大于30個后,聚類精度趨于穩定;其余兩種算法的聚類精度變化幅度較大,表示文獻[5]算法與文獻[6]算法對k值非常敏感,聚類精度受k值影響較大。表明本文算法加入的可變網格劃分方法可有效降低k值對聚類精度的影響,提升高頻數據共現聚類的準確性。實驗證明:在不同k值作用下,本文算法高頻數據共現聚類的準確性更高。 表5 不同k值作用下三種算法的執行時間 根據表5可知,隨著k值的逐漸增加,三種算法的執行時間均不斷提升,本文算法的執行時間明顯低于其余兩種算法,原因是本文算法中加入了可變網格劃分方法,能夠降低時間復雜度,提升高頻數據共現聚類的執行效率。實驗證明:在不同k值作用下,本文算法的高頻數據共現聚類的執行時間更短,有效提升高頻數據共現聚類的執行效率。 研究基于局部離群點檢測的高頻數據共現聚類算法,利用可變網格劃分的局部離群點檢測算法挖掘高頻數據共現對象,提升高頻數據共現聚類的執行效率。該算法雖在實驗中取得了很好的實驗結果,但還需不斷完善該算法。例如實施可變網格劃分時需要計算高頻數據集內的各個維度,在維度較高的情況下,該算法的計算量也相對較大,以后可以在該算法中加入降維等技術,進一步加快算法的執行效率。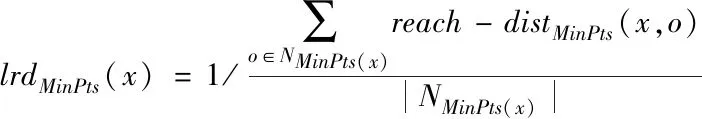

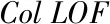
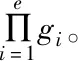
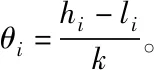

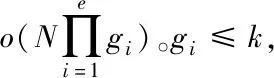



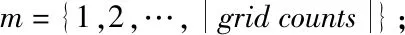
2.2 高頻數據共現聚類算法



3 實驗分析
3.1 離群點檢測性能分析
3.2 聚類的執行效率分析

3.3 聚類的準確性分析

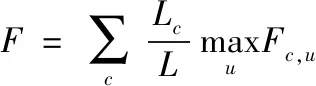

3.4 在不同k值作用下的聚類精度與執行效率分析


4 結論

