主干道信號燈通行可靠度量化評估仿真

薛煜亮，郝艷召

(1.西安工業大學，陜西 西安 710021；2.長安大學，陜西 西安 710064)

1 引言

城市交通堵塞大多處于交叉路口，主要是因為上、下段路徑的車輛通行能力不匹配。主干道信號燈通行能力主要受信號燈相位調控、道路通行能力等因素的影響。通過交通信號燈的調控對城市主干道交通運行狀態及效率進行調節，能夠在一定程度上減少交通擁堵情況的發生，使城市整體交通可以穩定、流暢的運行[1-2]。可靠度(Reliability)，也叫可靠性，是指產品在約定時段內，在一定的條件下，完成預定功能的能力，通常包括結構的安全性，適用性及耐久性，當以概率進行度量時，稱作可靠度。可靠度并非可見質量，一般需要進行定量評估。城市主干道信號燈通行可靠度評估以及量化分析是當前交通研究領域的熱點問題之一[3]。

針對城市主干道信號燈通行可靠度具有不確定性和難以定量分析的問題，在相關研究資料與實驗的基礎上，提出基于模糊綜合評價的主干道信號燈通行可靠度量化評估方法。采用模糊綜合評價方法將主干道信號燈通行可靠度的定性評價轉化為定量評價問題，解決了信號燈通行可靠度難以定量分析的問題。在此基礎上，運用疏解車距與等效車距分析主干道車輛的通行能力，以此來降低外界因素對主干道信號燈通行可靠度量化評估結果的影響，提升數據的可靠性與準確性。

2 主干道信號燈通行可靠度量化評估

2.1 主干道信號燈調控與車流通行能力分析

城市干道交通運行模型可近似看作以下幾類模型的綜合體：車流模型，道路交叉口模型，交通信號燈及其調控模型。結合Petri網構建城市主干道交叉路口模型[4]，通過實際數據分析可知，在城市主干道信號燈通行可靠度量化評估過程中，主要考慮主干道內道路交叉口與對應的交通信號燈相位調控模型[5]，城市主干道十字交叉路口及車道模型如圖1所示。

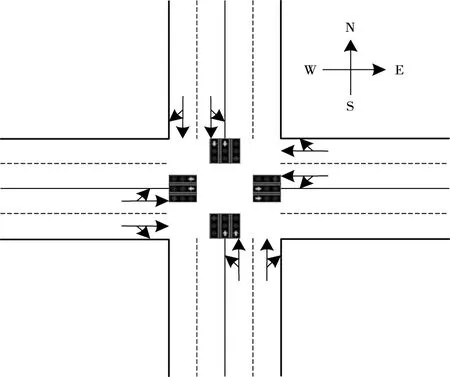
圖1 主干道交叉路口及車道模型

圖1中，各方向均為雙向車道，同時，四個方向進入該十字交叉路口的車流方向包括：直行及左、右轉向三種。

車道模型是用于描述道路上車流速度(v)與車流密度(k)相互關系的數學模型，根據主干道交叉路口及車道模型結合信號燈控制系統的固定相位順序以及當前應用的4相位調控方案，對車流通行方向與指示燈相位進行對應，如表1所示。

表1 交通信號燈相位調控方案

根據交通信號燈相位調控方案結合模糊控制理論對城市主干道交叉路口的交通流量進行檢測與調控。假設模糊控制的輸入值為X，該值為描述某一時間段內經過該交叉路口的車輛數量的變量，其對應的論域為Xi={6，12，18，24，30，36，42，48，54，60，66}，與之對應的車輛數量(車流長度)語言值K可分為七種：數量很多、數量較多、數量多、數量正常、數量少、數量較少和數量很少，將各值分別記作A1、A2、A3、M、B1、B2、B3，則變量X的隸屬度函數值如下表所示。

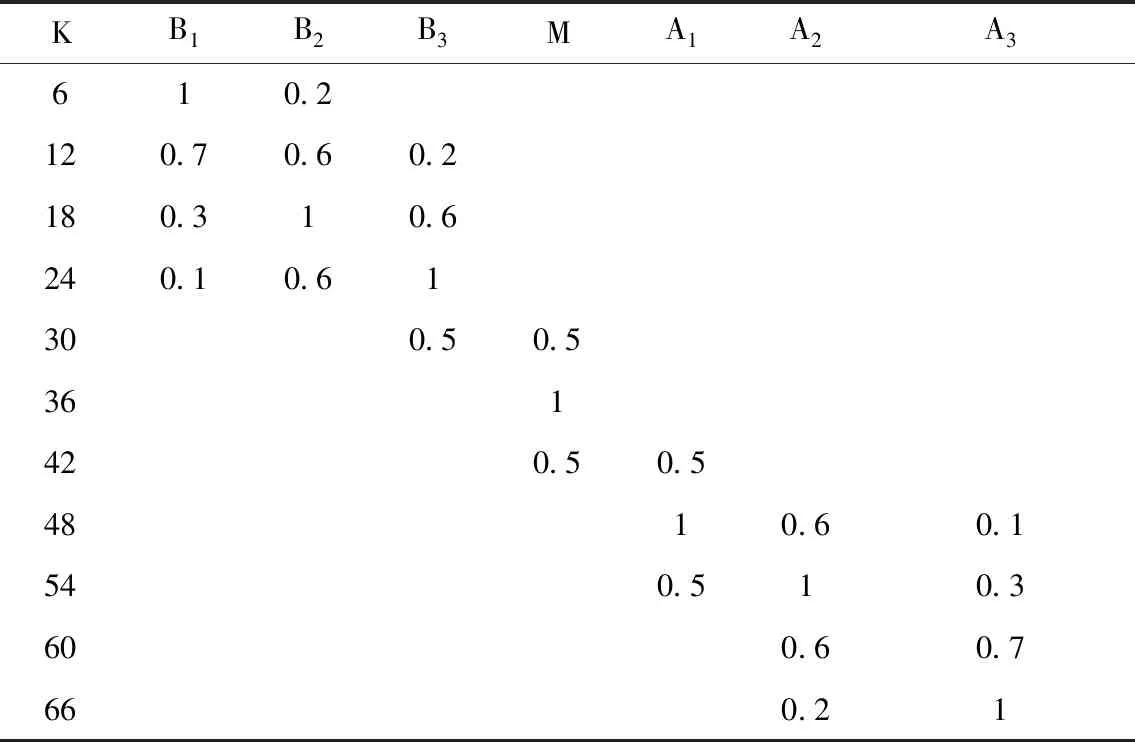
表2 變量隸屬度函數值

利用二維模糊控制器對交通信號燈進行相位調控，該調控過程對應的模糊控制規則為：if A and B Then C，據此，共可獲得49條調控規則，并歸納得到交通信號燈調控系統需要處理的車流量Y與橫、縱兩個方向的車流量Z的調控規則表，并對Y進行反模糊處理，進而獲取更清晰的數據信息。以所得數據信息及車流分類結果作為交通信號燈的相位調控要素，對城市主干道交叉路口的車輛通行狀況與時間進行狀態等級劃分[6]，結果見表3。

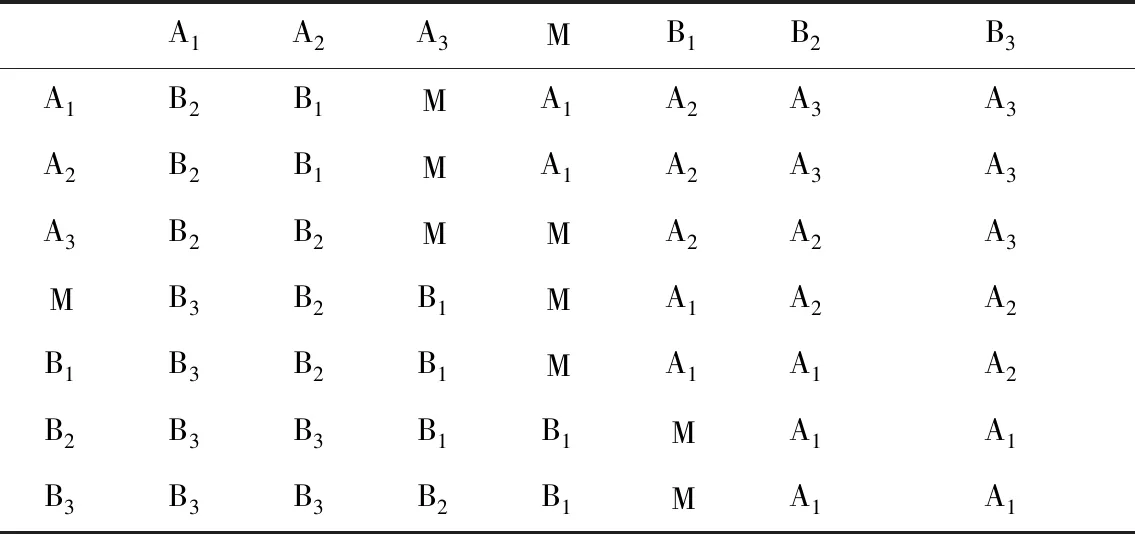
表3 交通信號燈模糊調控規則表

對于主干道車流量Y的分類情況為：將數量很多、數量較多和數量多劃為一類；數量正常單獨劃為一類；數量少、數量較少和數量很少劃為一類，劃分得到的三類分別記作大車流量、中車流量和小車流量。

為計算城市交通主干道車輛通行能力，在信號燈相位調控方案和主干道車流量分類結果的基礎上，引入疏解車距與等效疏解車距概念。疏解車距是指在交叉路口等候的車輛中，從綠燈亮起至隊列中第一輛車完全通過停車線的時間[7]，記作T，對應的計算式如下

T=Ts-Tg

(1)

其中，Ts代表等候的車輛中，排序第一的車輛的車尾經過停車線的時間點，Tg代表通行指示燈綠燈的啟亮時間點。

通過對疏解車距影響因素及其累積概率分布的分析，利用累積分布函數計算綠燈啟亮后隊列中的第一輛車的疏解車距T小于給定函數自變量t這一情況出現的概率Fr(t)。將T看作隨機變量，記作T(ξ)，設T(ξ)≤t，則有

(2)

引入疏解車距與等效車距分析主干道的車輛通行能力，能夠減少人為因素的影響，使得出的數據更加精準。在此基礎上，結合先驗結果，利用韋布爾分布來表達總體疏解車距中的個體，韋布爾分布能夠較好的體現城市主干路疏解車距的分布情況，擬合優度較好，誤差平方和極小，則對應的函數表達式為

(3)

其中，β表示形狀參數，用于調節車輛分布曲線的形狀；η表示尺度參數，用于調整車輛分布曲線的橫、縱軸標尺；γ表示位置參數，表征分布測試項起點，即疏解車距的最小值。根據數據分析可得，無行人及非機動車干擾的情況下，疏解車距的變化區間為[2s，6s]；存在干擾情況下，疏解車距的變化區間為[4s，9s]。其中，參數β和η會隨著干擾情況而發生變化，進而影響到累積疏解車距的分布情況。

綜合考慮駕駛員感知、反應時間以及車輛起動時間，綠燈啟亮后，駕駛員駕駛車輛離開停車線需要一定的時間。據此，分別以15%及85%疏解車距作為疏解車距的閾值下限值與上限值，給出等效車距定義。城市主干道信號燈車流調控交叉路口的等效疏解車距，即為累積頻率在15百分位到85百分位間的疏解車距的平均定積分值，經過累積頻率函數逆映射得到的結果，對應的計算式如下

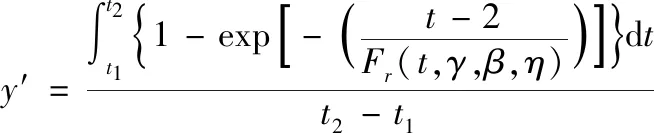
(4)

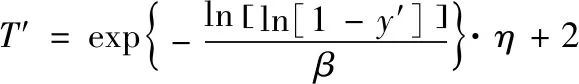
(5)

其中，y′代表等效分位值，t1、t2分別代表第15百分位和85百分位的疏解車距；T′代表等效疏解車距。

利用停車線方法計算城市主干道通行能力，對信號燈為綠色相位期間的車輛通行量進行估算，得到有效綠燈時間內機動車流量的估計值[8]。對比當前道路車輛通行能力分析算法，該方法的應用比較廣泛，且適用于城市主干道交叉口的實際交通狀態。利用式(6)給出車道通行能力C的計算公式：

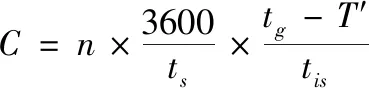
(6)

其中，n代表城市主干道的車道數量；tis代表車輛駛過停車線的間隔時間均值，通常為2s。

2.2 通行能力匹配與可靠性定量評估

以主干道信號燈調控與車流通行能力分析結果為基礎，引入匹配度ωxs來評判交叉路口通道上段路徑與下段路徑車輛通行能力的匹配程度，ωxs的值為下段路徑車輛通行能力Cx與上段路徑車輛通行能力Cs之間的比值，計算公式為

(7)

以該指標為城市主干道交叉路口車輛通行能力匹配程度的評判基礎，理想條件下，ωxs的值為1時，信號燈上段路徑與下段路徑車輛通行能力匹配結果處于最佳狀態，綜合考慮各時段及不同路段的車輛數量波動性，以及算法與基礎設施設計的差異性，將0.9≤ωxs≤1.1這一區間，看作實際應用中上、下段路徑車輛通行能力匹配度的較優狀態[9]。若ωxs<0.9，說明下段路徑的車輛通行能力不足，無法完全承載上段路徑的通行車輛；若ωxs>1.1，說明下段路徑的車輛通行能力未能完全利用，其中部分通行能力浪費。

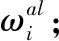
(8)

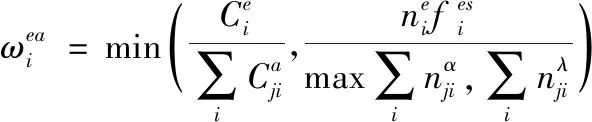
(9)

(10)

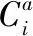
根據上述分析結果，結合模糊綜合評價法進行主干道信號燈通行可靠度量化評估，該方法廣泛應用于不確定性問題的描述，能夠較好的解決難以定量的模糊性問題。

假設主干道信號燈通行可靠度的影響因素集合為U=(u1，u2，…，um′)，主干道信號燈通行可靠度的評價集合為V=(v1，v2，…，vn′)，影響因素um′對評價結果vn′的隸屬度為rm’n′，得到綜合評價矩陣R的規模為m′×n′。對應的表達式如下

(11)

假設主干道信號燈通行可靠度影響因素的重要性模糊子集為S′=(s1，s2，…，um′)，其中，s代表影響因素ui′對最終評估結果影響程度的度量值，得到模糊綜合評估集合FC=S′R。

根據信號燈及道路網結構，將主干道信號燈通行可靠度的影響因素劃分為路徑集合、道路單元集合，逐層運算后獲得最終的可靠度評估結果，本文選擇車流通行的暢通程度作為可靠性評估指標。

根據相關調研結果，將主干道信號燈通行可靠度分為5個等級，分別為：嚴重堵塞、基本堵塞、輕微堵塞、基本暢通、非常暢通，對應的可靠度值分別設定為0.0～0.1，0.1～0.25，0.35～0.5，0.5～0.8，0.8～1.0。

設分級后的影響因素U、Ui′的重要程度子集分別為S′和Si′，則主干道信號燈通行可靠度，即車流通行流暢程度的模糊綜合評估結果如下

={FC1，FC2，FC3，FC4，FC5}

(12)

根據以上計算結果，綜合最大隸屬度原則實現主干道信號燈通行可靠度的量化評估。

3 實驗結果與分析

為檢驗基于模糊綜合評價的主干道信號燈通行可靠度量化評估方法的綜合有效性，進行實驗。實驗中的信號燈為兩相位信號，設定的分位道路包括左、右轉向專用車道與直左、直右共用車道兩種類型，實驗中設定的交通條件如表4所示。實驗中，道路車輛通行能力的單位為pcu/h，車道數量單位為條。

表4 實驗預設交通條件

在以上實驗預設條件的基礎上，采用所提方法進行實驗，得到轉向車道類型不同時對應車道車輛通行能力可靠度變化曲線如圖2所示，信號燈通行能力可靠度與沖突行人、非機動車流量的關系如圖3所示，設機動車流量均值為MT。

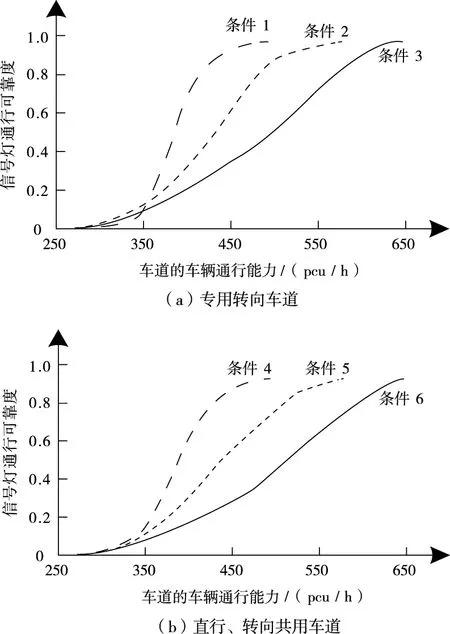
圖2 轉向車道車輛通行能力可靠度變化曲線

根據圖2(a)和(b)可知，在不同條件下，轉向車道車輛通行能力可靠度最高值均接近于1.0。無論是專用的轉向車道，還是直行、轉向共用車道，在車道車輛通行能力相同的情況下，隨著行人與非機動車流量的增加，對應的信號燈通行可靠度呈現下降趨勢；車道的車輛通行能力及行人與非機動車流量相同時，專用轉向車道的信號燈通行能力較高。由圖3可以看出，沖突行人與機動車數量越高，信號燈通行可靠度越低；機動車流量均值越高，對于行人與非機動車的干擾越敏感，信號燈通行可靠度變化越明顯。

4 結束語

本次主干道信號燈通行能力研究，在以信號燈節點道路、交通與信號調控條件為主的前提下，添加了上、下段路徑車輛通行能力與匹配程度的分析，經實驗驗證得出：

1)該方法有效解決了主干道信號燈通行可靠度的不確定性，得出在不同條件下，專用轉向車道和直行、轉向共用車道車輛通行能力可靠度最高值均接近于1.0，實現了定量分析。

2)在對主干道車流量分類的基礎上，結合疏解車距與等效車距分析主干道的車輛通行能力，分析結果符合實際條件。

主道路車輛通行能力計算與探究是一個持續發展的過程，同時，城市主干道信號燈通行能力的非定性分析是相關領域研究的重要方向之一，今后的研究中，還要深入探究交通整體環境以及天氣狀況等其它外界因素的影響。