基于能量耦合的欠驅動三維BC防擺控制
吳向明,范 波,張啟啟,宋曉明
(河南科技大學信息工程學院,河南 洛陽 471023)
1 引言
欠驅動系統以其獨立控制變量個數小于系統自由度個數的特性被廣泛地應用于各個領域。橋式起重機作為典型的欠驅動控制系統,在短距離場地運輸中發揮著重要的作用。
由于運行環境的要求,橋式起重機一般是由經驗豐富的工人操作,但介于橋式起重機系統的高度非線性和控制量少等原因,給其控制帶來了極大的挑戰。這就導致橋式起重機系統普遍存在工作效率低下和安全性能不高等問題。為了提高橋式起重機系統的工作效率與安全性能,國內外許多學者對橋式起重機系統進行了大量的研究:Garrido等人[1]通過輸入整形技術在特定脈沖序列對模擬信號進行卷積以減少負載擺動。董明曉等人[2]以基于載荷擺動幅值最小及優化時滯的思想設計最優輸入整形器。Fang等人[3]從能量角度來增強臺車與負載之間的動態耦合關系,使得橋式起重機控制性能得到了提升。馬博軍等人[4]設計了一種基于耗散理論的自適應控制器,實現了對整個橋式起重機系統的快速控制。Fang等人[5]構造一條S形定位軌跡,并設計自適應跟蹤控制器消除負載擺動。
上述研究均以二維平面內的橋式起重機系統模型為基礎展開,而在實際應用中,橋機和吊重多數情況下都在三維空間內運動。由于三維橋式起重機系統模型更接近實際橋式起重機,包含更多的狀態量,且各個狀態之間相互耦合,非線性更強,增加了吊重擺動控制的難度,因此其研究具有更大的實踐價值。文獻[6]中,孫寧等人設計了一種目標軌跡自適應控制器,雖然具有良好的控制性能和不錯的適應性,但該方法應用時須進行參數在線估算。文獻[7]中,Zhang等人通過引入兩個新的復合信號,構造新的存儲函數,設計跟蹤控制策略,使得系統具有較好的暫態性能和較強的魯棒性;文獻[8]中,Sun等人通過引入虛擬有效載荷,分別對系統動能及勢能整形,設計出一種能量耦合的輸出反饋控制律,實現了小車精確定位和有效載荷擺動消除。雖然上述控制策略均有較好的定位和防擺控制效果,但是它們均過于依賴系統模型且控制器設計和分析較為復雜。
針對上述控制策略中過度依賴模型參數、控制方法復雜的問題,本文設計了一種基于能量耦合的三維橋式起重機防擺控制方法。首先,基于定繩長三維橋式起重機數學模型,分析系統能量,結合三維坐標系中臺車與負載的耦合關系,建立基于負載空間位移誤差的復合控制信號;然后,利用李雅普諾夫方法,獲取能量耦合控制律,并通過LaSalle不變性原理證明系統的有界性與收斂性。最后,進行仿真驗證,并與傳統的PID控制及能量控制方法對比,說明該方法能夠實現臺車的定位與負載消擺,且具有更佳的控制效果;同時減少調節參數,降低模型參數依賴度,簡化控制律。
2 三維橋式起重機模型分析
橋式起重機主要依靠大車、臺車和吊繩的運動來完成對負載的挪移,由此建立橋式起重機的五自由度三維數學模型[9],其系統模型如圖1所示。

圖1 三維橋式起重機模型示意圖
其中,Mx,My分別表示x,y方向上運動的等效質量(因為臺車沿y方向運動時,導軌隨之一起運動,所以Mx主要是(小車的質量)臺車的質量,而My主要包括臺車和橋架的質量);θx表示吊繩在xoz平面上的投影與z軸負方向所成的夾角,θy表示吊繩與xoz平面的夾角;l表示擺繩長度;m表示負載的質量;fx,fy分別表示沿x,y方向上的力;(xm,ym,zm)表示負載質心坐標。
對于固定繩長的三維橋式起重機系統而言,其動力學模型可描述如下[10,13,14]
mlxcosθxcosθy-mlysinθxsinθy-
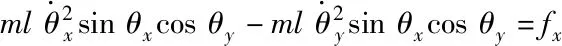
(1)

(2)
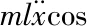

(3)

(4)
由圖1可知,負載的水平位置信號可表示為
xm(t)=x+lsinθxcosθy
ym(t)=y+lsinθy
(5)
將式(5)關于時間t求導,可得
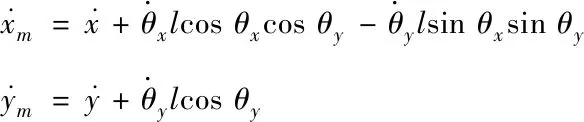
(6)
根據實際運行情況,負載擺角θx(t),θy(t)∈(-π/2,π/2),負載的水平位移包含臺車位置與負載擺角的耦合信息,為控制器的設計提供條件。
3 能量耦合控制器設計
3.1 系統無源性分析
根據橋式起重機的動力學模型,該系統能量可以表示為
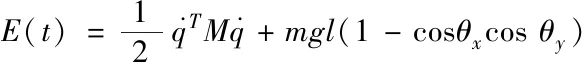
(7)
對式(7)關于時間t求導并整理可得[11,12]
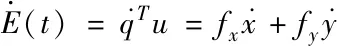
(8)
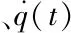


(9)

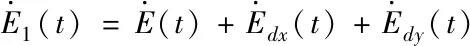
(10)
對式(10)關于時間t求積分,可得
E1(t)=E(t)+Edx(t)+Edy(t)=E(t)+Ed(t)
(11)


(12)
將式(3)和(4)代入式(12)整理可得
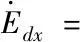
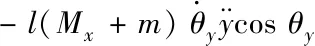
(13)
對式(13)關于時間t求積分有
Edx=-l(Mx+m)

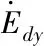
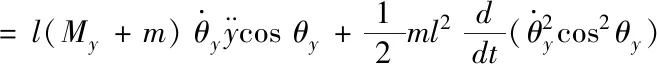
(14)
對式(14)關于時間t求積分有
則
Ed(t)=Edx(t)+Edy
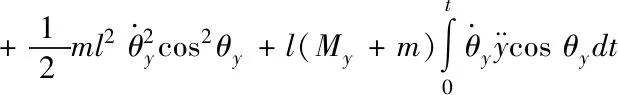
(15)
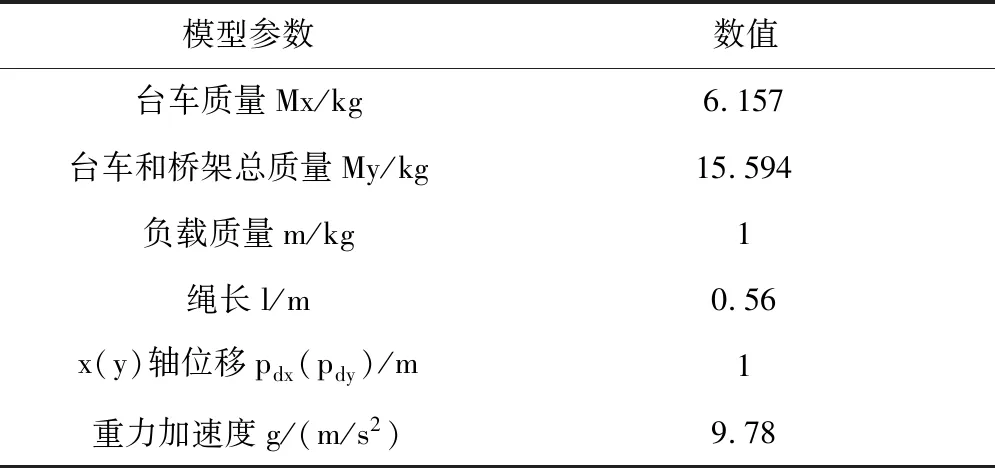
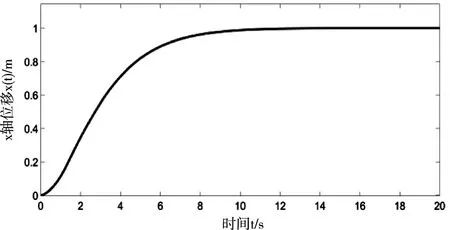
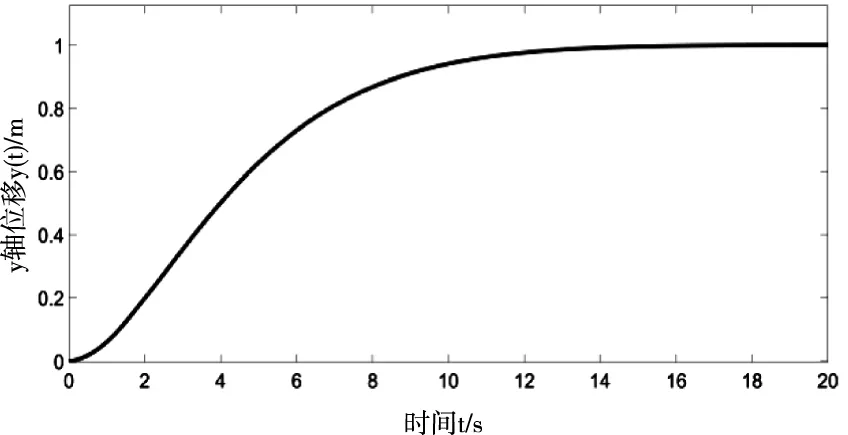
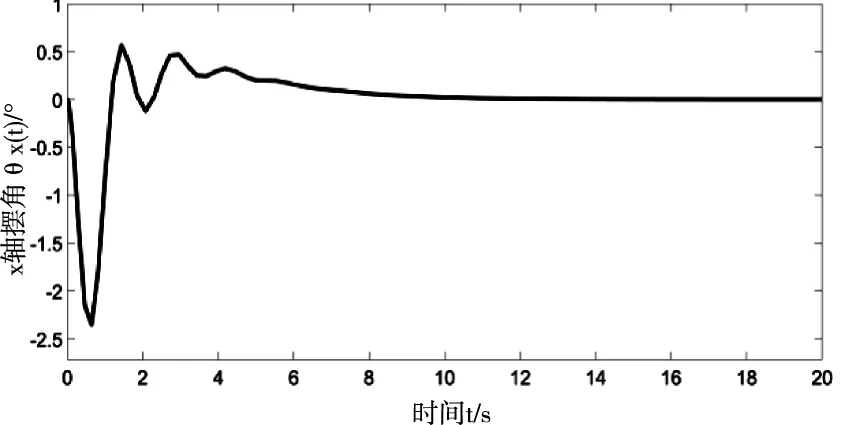
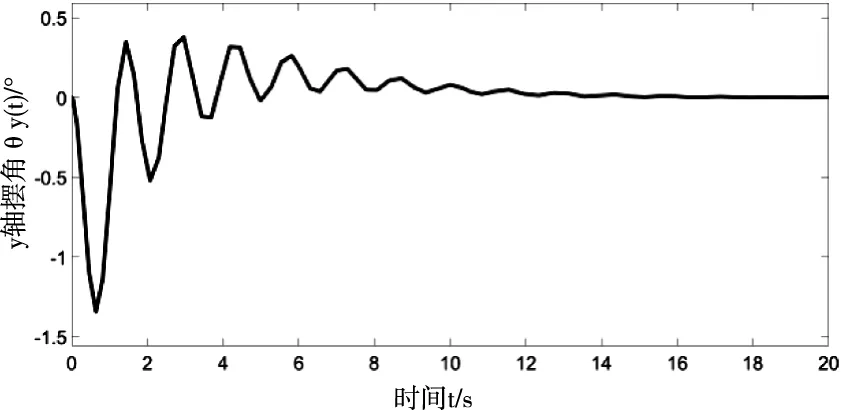
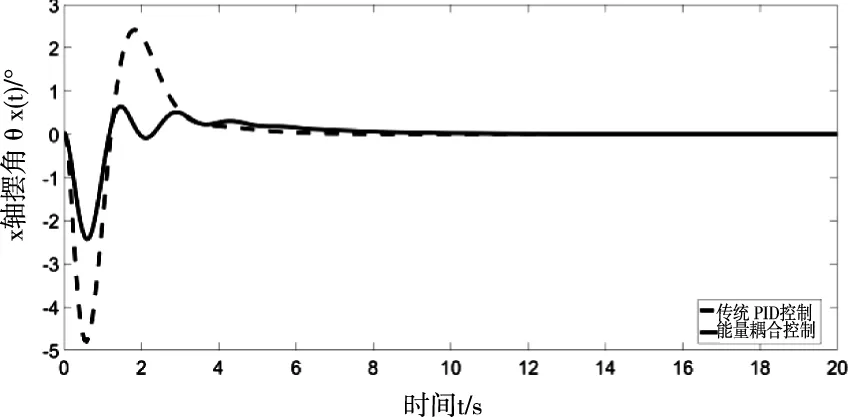
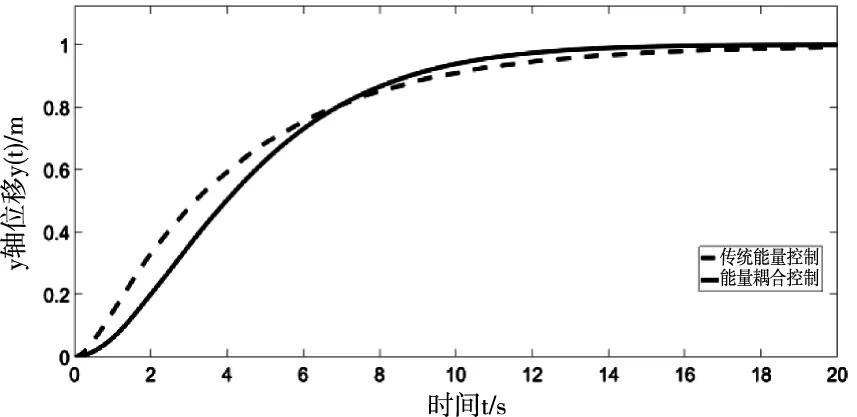
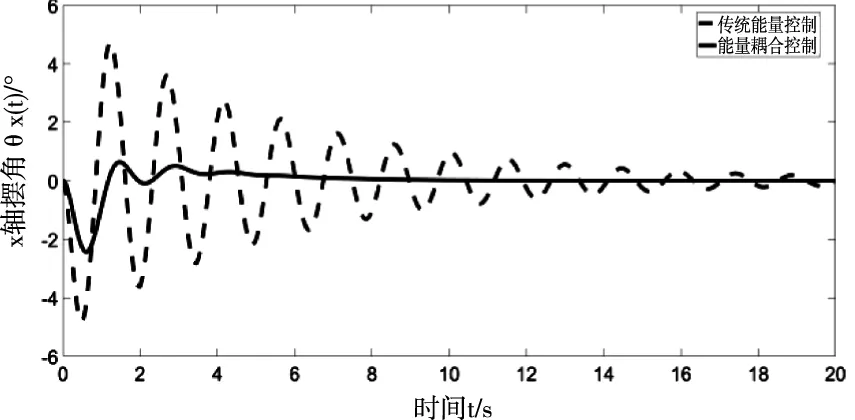
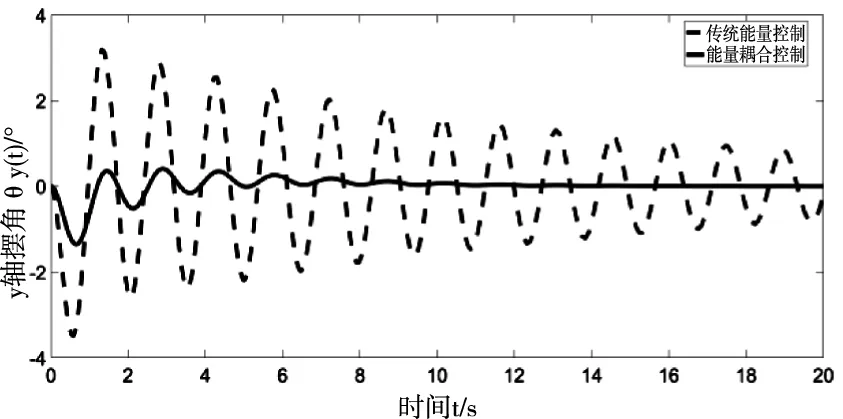
因為Mx -gl(Mx+m)(1-cosθxcosθy) (16) 令 由于θy(t)∈(-π/2,π/2)?cosθy>0,可得如下結論 將式(7)、(15)代入(11)并整理可得 E1(t)=E(t)+Edx(t)+Edy(t)=E(t)+Ed(t) ≥0 (17) 從E(t),Ed(t)正定性可知,式(17)中新型儲能函數E1(t)也為正定。 橋式起重機的控制的目標是在時間t1內臺車到達指定位置pdx、pdy,同時有效抑制并消除負載擺動,即 負載水平運動的定位誤差信號εx(t)與εy(t)為 εx(t)=xm-pdx=ex+lsinθxcosθy εy(t)=ym-pdy=ey+lsinθy (18) 式中,ex(t)=xm(t)-pdx,ey(t)=ym(t)-pdy分別為臺車在x,y方向上的定位誤差。 選取李雅普諾夫候選函數 (19) 式中kpx>0,kpy>0。 對式(19)求導,可得 (20) (21) 其中,kdx>0,kdy>0。 臺車在耦合控制方法(21)作用下,可迅速到達目標位置,并有效地消除負載擺動,即 由式(20)、(21)可知 (22) 所以V(t)為減函數且V(t)>0,因此V(t)有界。由式(18)、(19)及(21)知 (23) (24) 進一步可知 εx(t)=ex+lsinθxcosθy=A εy(t)=ey+lsinθy=B (25) =0 (26) (27) 其中,A,B為待定常數。則由式(21)、(24)、(25)可得在集合Ψ中 fx(t)=-kpxA,fy(t)=-kpyB (28) 將式(26)、(27)重新整理可得 (29) (30) 將式(1)、(2)整理可得 (31) (32) 結合式(28)、(29)、(30)、(31)、(32)可得 (33) A=0,B=0 (34) 結合式(25)、(28)、(33)可知,在集合Ψ中 εy(t)=0,fx(t)=0,fy(t)=0. (35) (36) (37) 將式(35)、(37)代入式(3)和式(4),可求得 gsinθxcosθy=0 gcosθxsinθy=0 (38) 又因為cosθx>0,cosθy>0,有 θx=0,θy=0 (39) 假設a≠0,b≠0,結合式(25)、(34)、(36)可得sinθxcosθy=-a/l≠0,sinθy=-b/l≠0,與式(39)的結論相矛盾,由此可知a=0,b=0。由式(36)得 ex(t)=0,ey(t)=0 (40) 綜上,由式(36)、(37)、(39)、(40)結論可知,最大不變集Ψ僅包含平衡點。根據LaSalle不變性原理[15],基于負載能量耦合控制律(21)能夠滿足臺車到達指定位置并消除負載擺動。即 基于MATLAB/simulink仿真平臺驗證上述基于能量耦合控制器消擺性能。仿真模型參數,見表1。仿真結果,如圖2、圖3、圖4、圖5、圖6、圖7、圖8、圖9、圖10、圖11、圖12、圖13所示。 表1 仿真模型參數表 圖2 能量耦合控制x軸方向位移變化曲線 圖3 能量耦合控制y軸方向位移變化曲線 圖4 能量耦合控制x軸方向擺角變化曲線 圖5 能量耦合控制y軸方向擺角變化曲線 圖2、圖3中,臺車在x軸方向和y軸方向均能到達指定位置。但y軸方向總質量更重,到達指定位置時間耗時更長。 圖4、圖5中,臺車在x軸方向和y軸方向均能實現消擺功能。但y軸方向總質量更重,產生的摩擦更大,且相比于x軸方向y軸的耦合情況更為復雜,受到外界干擾更多,因此y軸方向產生的殘余擺動更難消除。 圖6 能量耦合與PID控制x軸方向位移變化曲線 圖7 能量耦合與PID控制y軸方向位移變化曲線 圖8 能量耦合與PID控制x軸方向擺角變化曲線 圖9 能量耦合與PID控制y軸方向擺角變化曲線 圖6、圖7中,與傳統PID控制相比,能量耦合控制在臺車定位方面消耗的時間更長,但能量耦合控制在位移變化前段和后段臺車加速度變化更加平緩,負載運動時產生的擺動相對更小,使橋式起重機操作更加安全。 圖8、圖9中,能量耦合控制與傳統PID控制均能在短時間內完成負載消擺,兩者在消除負載殘余擺動方面效果相差無幾,但能量耦合控制在抑制負載擺角上具有更好的控制效果。 圖10 能量耦合與傳統能量控制x軸方向位移變化曲線 圖11 能量耦合與傳統能量控制y軸方向位移變化曲線 圖12 能量耦合與傳統能量控制x軸方向擺角變化曲線 圖13 能量耦合與傳統能量控制y軸方向擺角變化曲線 圖10、圖11中,與傳統能量控制相比,能量耦合控制具有更好的位移曲線,能夠更快的實現臺車定位。能量耦合控制在位移變化前段臺車加速度變化更加平緩,負載運動時產生的擺動相對更小,位移變化后段具有更加迅速的定位效果,在指定位置附近能夠迅速定位。 圖12、圖13中,傳統能量控制負載擺動時產生較大的擺角且負載殘余擺動較為強烈,不能在短時間內完成負載的消擺工作。而負載能量耦合控制在抑制負載擺角,消除殘余擺動方面均具有良好的控制效果。 通過仿真結果對比分析可知,該方法能夠在橋式起重機運行過程中有效抑制負載擺動,實現臺車準確定位;與傳統PID控制和傳統能量控制相比,能量耦合控制能夠有效抑制擺角并且對殘余擺動有一定程度的消減,具有更好的消擺效果。 針對欠驅動三維橋式起重機防擺控制問題,本文通過分析三維橋式起重機系統能量,構建負載空間位移誤差信號,利用李雅普諾夫方法,設計了基于能量耦合的定繩長三維橋式起重機防擺控制方法,并對控制器的性能進行了嚴格的理論分析。通過仿真對比,驗證了該方法能夠實現臺車定位與負載有效消擺。在未來的工作中,將考慮提升臺車的快速定位性能,以獲得更好的控制效果。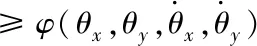
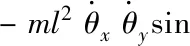


3.2 能量耦合控制器設計





3.3 控制器穩定性分析
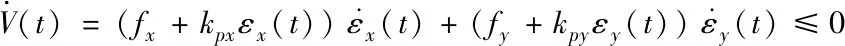


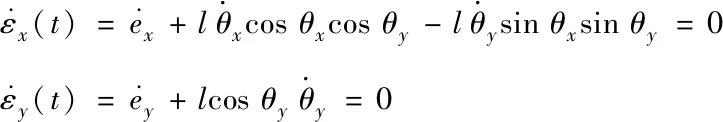
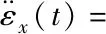

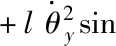
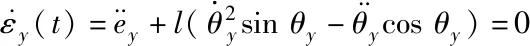
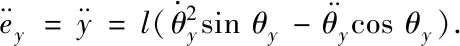


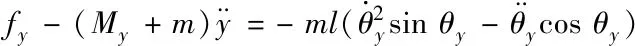

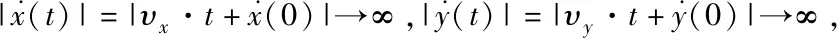



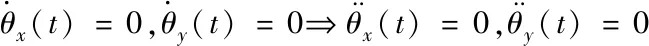
4 仿真結果及分析




5 結論

