基于SMPL模型的人體姿態估計

李 健，楊鏢鏢，張皓若

(陜西科技大學電子信息與人工智能學院，陜西 西安 710021)

1 引言

三維人體建模一直以來都是三維重建研究領域一個比較富有挑戰性且比較重要的部分，其本質在于將現實世界中的人體以三維數字化的方式在計算機中存儲并表示。高質量的人體三維模型在數字媒體創作、人體測量、虛擬試衣、游戲、三維動畫、虛擬現實等領域有著廣闊的應用前景。目前主流的三維人體建模方法主要分為以下三種：三維建模軟件建模，即利用3D Max、Sketch up、Maya等基于計算機圖形學原理開發的三維建模軟件來生成人體三維模型；大型3D激光掃描儀建模，即通過Artec、RIEGL VZ-1000 等大型掃描設備對物體表面投射激光點陣，不斷掃描并獲取其三維信息；基于計算機視覺的三維人體建模，即使用普通RGB相機或深度相機來進行人體建模。基于計算機視覺人體的三維建模可以根據兩個標準進行分類：一是基于模型先驗，二是自由形式。基于模型先驗的方法是利用參數化的人體模型來進行人體姿勢和形狀的估計[1]。隨著人體二維關鍵點檢測的進步，從單個圖像直接對主要關節和粗略3D姿勢進行3D估計方面也取得了進展[2-3]。2016年，Bogo F等人提出利用多個人體先驗從檢測到的14個二維關鍵點恢復線性模型參數[4]。然而，人體具有高度的復雜性和靈活性，從二維圖像中恢復三維人體姿勢和形態仍然具有很大的挑戰。利用卷積神經網絡(Convolutional Neural Networks，CNN)來回歸參數模型可以一定程度上解決這一問題。2018年，Kanazawa A 等人提出利用基于回歸的人體網格重構(Hot Module Replacement，HMR)算法[5]恢復人體姿態，但是其在自然圖像中的表現仍然有待提高。隨后，Alldieck T等人提出一種利用單目視頻結合人體線性模型進行人體動態重建的方法，該方法可以將人體線性模型投影到人體輪廓當中，但是需要特定動作配合[6]。基于模型先驗的方法可以適應更復雜的人體姿態，只需要少量的數據就可以獲得粗略的模型，雖然模型缺乏準確性，但效率更高，也更簡便。因此，基于模型先驗的方法更適用于精度較低但效率較高的環境下。在基于自由形式的方法下，2016年Innmann M提出實時重建非剛性體[7]，然而需要輸入高質量的多視圖，這就限制了實際應用時的使用環境。2017年，Zhu H等人提出利用RGB視頻對室外環境中穿著衣服的人體進行重建[8]，但是該方法要求人體長時間靜止不動，使用范圍受限。綜上，現階段基于自由形式的人體建模的方法的研究，對采集設備或者人體姿態要求較為苛刻，且模型內部沒有裝配動畫骨架。因此，本文采用基于模型先驗的人體建模方法。

2015年馬普所提出了由姿態與體型參數驅動的蒙皮多人線性模型[9](Skinned Multi-Person Linear model，SMPL)，2018年Cheng Z Q等人[10]曾比較了Dyna[11]，SMPL和RealtimeSCAPE[12]幾個典型的參數人體模型，得出SMPL模型在速度和準確性方面都比其它模型具有更好的表現，同時SMPL模型與現有的渲染引擎兼容。考慮到設備的便捷配置，本文僅使用單一設備。基于以上分析，本文使用單個Kinect相機和SMPL模型來進行人體三維數字化建模。

目前基于人體形變模型的姿態估計工作大多集中于單幀靜態圖像，由于單一視角的二維圖像會丟失三維上的信息，在映射到三維姿態的時候，會產生一些不真實的姿態。為了解決上述問題，本文提出利用Kinect相機得到的人體三維骨架，擬合到SMPL模型上，彌補了二維圖像映射到三維姿態時的缺失信息，從而提高了人體重建模型的準確度。

2 相關工作

2.1 SMPL人體模型

SMPL模型是一種參數化人體模型，該模型可以通過參數的改變進行任意的人體建模和動畫驅動。其輸入是10個體型參數(β，包含人的高矮胖瘦和頭身比)和72個姿態參數(θ，包含24個關節相對角度)。將模型形狀參數β和動作參數θ作用于基礎模板Tμ進行動作變形，得到重構出的模型M(β，θ)以及模型的網格頂點位置T(β，θ)[9]。

M(β，θ)=W(T(β，θ)，J(β)，θ，ω)

(1)

T(β，θ)=Tμ+Bs(β)+Bp(θ)

(2)

其中W是一個混合蒙皮線性方程，其包含：

1)將β體型參數對應到骨骼關節的函數J(β)。

2)將θ姿態參數映射到模型對應點的變形函數Bp(θ)。

3)將β形狀參數映射到模型對應點的變形函數Bs(β)。

4)各個關節的混合權重ω。

2.2 HMR算法

HMR算法是一個端到端的從二維人體圖像恢復出三維人體模型的算法框架，算法網絡框架如圖1所示。

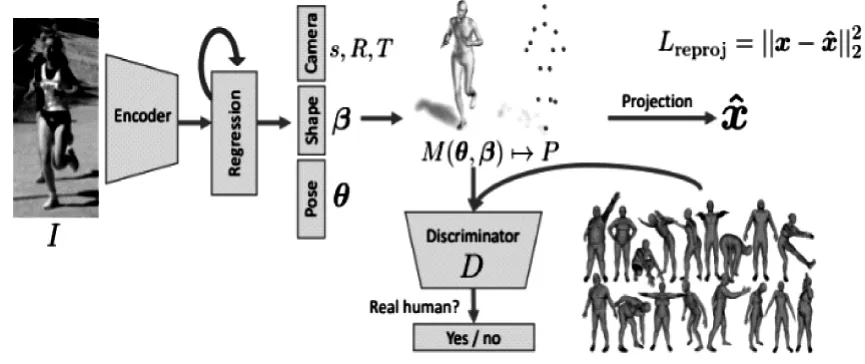
圖1 HMR算法網絡架構

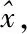
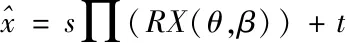
(3)

(4)

通過HMR算法估計的人體模型如圖2所示。從圖2中可以看出，算法在細節處(圖2中圓圈所示)仍然存在一定誤差。

圖2 HMR算法結果

3 算法總體設計

基于SMPL模型的人體姿態估計中最主要的問題是如何將標準模板與真實數據進行非剛體配準，實質上就是為標準模板尋找合適的體型參數β和姿態參數θ，從而使β和θ所描述的人體模型與輸入的真實數據實現最優配準。本文設計了一種基于SMPL模型的人體姿態與形狀估計的方法，具有準確、快速的特點，能夠在較短時間內生成一組完整的三維人體模型。該模型能夠準確描述人體的真實姿勢與形狀，重建流程如圖3所示。首先，具有任意姿勢的用戶站在Kinect傳感器前，通過Kinect獲取人體骨骼點信息，利用HMR算法從單張圖片得到SMPL模型。然后利用迭代最近點(Iterative Closest Point，ICP)算法將SMPL模型的關節點和Kinect骨架點轉換到同一坐標系下進行配準。接下來通過建立目標函數，迭代地將SMPL模型擬合到運動骨骼點上，得到優化后的模型。最后，利用攝像機標定獲得的相機內、外參數將模型投影到相應的彩色圖像上，得到近似于人體姿態的模型。

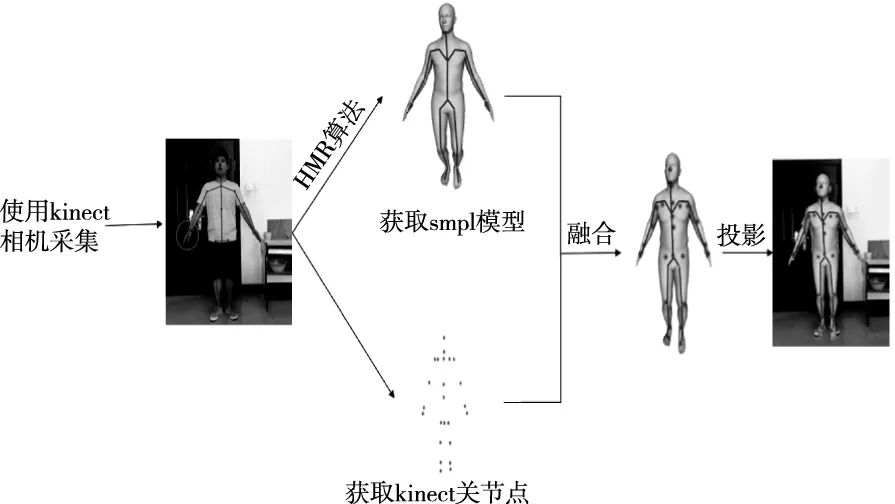
圖3 重建流程

3.1 θ的整體剛性變換

姿態參數θ表示相對關節之間旋轉的軸角，J(β)為根據人體形狀參數β預測3D骨骼關節位置的函數[9]。然而通過J(β)得到的三維關節點只代表當前坐標系下所在位置，為了得到統一坐標系下SMPL的各個關節信息，需要進行全局剛性變換。對于關節i，將3D關節表示為Rθ(J(β)i)，其中Rθ代表由姿態θ引起的整體剛性變換[9]。本節將介紹如何進行這一變換。

羅德里格斯公式(Rodriguez formula)是計算機視覺中的一大經典公式，經常用于描述相機位姿的過程中。公式如下所示

R=I+sin(θ)K+(1-cos(θ))K2

(5)

I是單位向量，K代表旋轉軸向量，θ是旋轉角度，R代表旋轉矩陣。通過使用羅德里格斯公式將每兩個關節的軸角轉換為局部旋轉矩陣。當得到兩個相對關節之間的局部旋轉及其位置時，然后可以使用坐標的傳遞性來計算全局旋轉變換和平移變換。

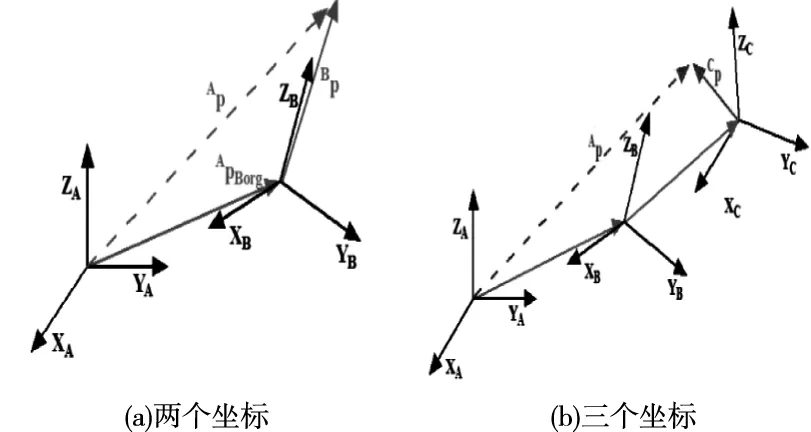
圖4 同一點的坐標變換

如圖4(a)所示，AP是坐標A中某一點的位置，BP是坐標B中同一點的位置，APBorg等于向量AP-BP，通過如下變換可以得到AP

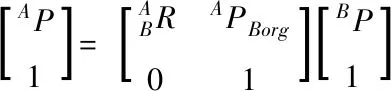
(6)

在圖4(b)中，可以通過使用等式(7)將坐標系C中的CP轉換成BP，并通過等式(8)將CP轉換成坐標系A中的AP

(7)

(8)

通過上述變換，可以將不同坐標系下的SMPL各個關節統一到同一坐標系下，最終可以得到SMPL的完整骨架信息，如圖5所示。

圖5 3D骨架

3.2 將Kinect坐標轉換為SMPL

由于SMPL三維關節與Kinect關節所在坐標系不同，需要將Kinect關節與SMPL關節變換為同一坐標系下。ICP算法是一種基于對應點的計算出最優旋轉和平移的算法，常用于對齊兩個點集。在已知對應點的情況下，有如下解決方案。

找到最佳剛性變換有如下幾個步驟：首先，找到Kinect坐標點集A和SMPL坐標點集B的質心；其次將兩個數據集都帶到原點，最后找到最佳旋轉R和平移T。

將兩個數據集移動到原點后，計算協方差矩陣H，H矩陣定義如下

(9)

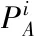
通過奇異值分解(SVD)計算得到最優旋轉矩陣R[13]。

H=USVT

(10)

R=VUT

(11)

H是一個m×n的矩陣，U是m×m的矩陣，S是m×n的矩陣，V是n×n的矩陣。

通過式(12)得到平移向量T。

T=-R×CentroidA+CentroidB

(12)

最終通過式(13)將Kinect坐標轉換到SMPL對應的坐標系上。

PSMPL=RPKinect+T

(13)

如圖6(a)所示，顯然，上方所在關節(Kinect關節)與下方關節(SMPL關節)之間的距離較遠。由于軀體的剛性特質，將軀干關節作為對應點來求解旋轉矩陣R和平移向量T，最終將兩組點集統一到同一坐標系下，轉換的結果如圖6(b)示。

圖6 使用ICP算法的比較

3.3 構造目標函數

利用HMR算法獲得了人體的β，θ參數，然后通過θ得到SMPL的三維關節位置，接著將SMPL模型的姿態擬合到Kinect關節上。圖7展示的是Kinect與SMPL骨骼點的比較。

圖7 Kinect與SMPL骨骼點的比較

首先，可以看到Kinect在圖7(a)中有21個關節(實際上在Kinect中刪除了手上的4個關節，因為不需要這些)，而SMPL模型在圖7(b)中有24個關節，然而它們的關節并非一對一的。所以需要將Kinect的關節映射到SMPL模型上。例如，Kinect關節的索引12映射到SMPL關節的索引1。SMPL中有3個關節是分別索引6、13、14，而Kinect中沒有對應的索引，所以需要計算它們周圍點的平均值來求解它們的值。

此時需要建立一個目標函數來表示對應關節點的差異，并且盡可能最小化目標函數。目標函數公式如式(14)所示。

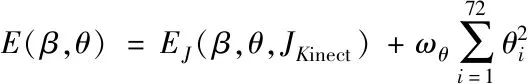
(14)

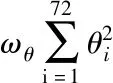
(15)

文獻[5]使用的能量函數E(β，θ，J2D)，僅利用二維骨架的約束進行優化求解，不能精確的求解人體的真實姿態。本節提出的能量函數EJ(β，θ，JKinect)建立在Kinect三維骨架信息的基礎上，通過求解對應關節點的最小歐式距離，得到相應的姿態參數。其中Joint代表對應的關節點個數24，wJ表示關節對應的權重，Rθ(J(β)i)代表θ全局剛性變換后得到的三維關節[9]，J(Kinect，i)表示對應的Kinect關節坐標。

在具體的實驗過程中，利用Kinect相機獲得三維骨骼點，通過SMPL模型得到三維關節點，在同一坐標系下，構造關節誤差的目標函數，利用基于梯度的Dogleg法[14]最小化目標函數，得到相應的體型參數β和姿勢參數θ。然后輸入到SMPL得到完整的三維人體模型，并將得到的人體模型投影到彩色圖像上。

4 實驗結果及分析

4.1 實驗環境

利用本文算法可以對自由移動的人體進行姿態估計。實驗中將Kinect相機固定，人在Kinect相機前做任意動作，就可以得到與人體動作相似的人體模型。本實驗以Kinect采取的六幀數據為例，詳細分析本文算法在實驗中的具體步驟，并與HMR算法和文獻[6]算法進行比較。實驗環境如下：

1)電腦配置：Intel Core i5-8300H CPU/16G，NVIDIA GeForce GTX1060Ti顯卡/GPU 加速；

2)數據來源：Kinect相機。

3)算法實現：Chumpy、Opendr渲染庫/Python語言。

4.2 實驗結果

HMR算法是通過單張圖片恢復人體模型，而文獻[6]算法是利用彩色圖的輪廓信息優化SMPL模型，選取這兩種算法與本文算法進行對比。實驗結果如圖8所示，其中圖8(a)為深度相機采取的彩色圖，圖8(b)為深度相機采集的3D關節圖，圖8(c)為本文算法重建出的模型投影圖，圖8(d)為HMR算法的模型投影圖，圖8(e)為文獻[6]算法的模型投影圖。

圖8 姿態估計算法對比

HMR算法不僅體形上與彩色圖人體差距較大，而且在一些細微的姿勢上，不能很好的與人體重合，如手臂、腳部、膝蓋等；而文獻6算法僅限在A型姿勢估計時效果較好，但與本文算法相比，仍然有所不如，且復雜姿態下得到的結果與真實人體姿態相比差異較大。如圖8(c)所示，圖中黃色圓點代表Kinect關節，綠色圓點代表SMPL關節點，藍色代表SMPL骨架，可以看出，SMPL骨架能較好的擬合到Kinect關節上，從而使得得到的人體模型更接近真實人體。相比其它兩個算法，本文方法能夠將三維模型較為準確的投影到彩色圖像上，有效估計了人體的三維姿態。

為了驗證本文方法的有效性，選取豪斯多夫(HuasdOrff)距離來計算模型關節與Kinect關節點之間的均方根(Root Mean Square，RMS)誤差。與歐式距離不同，Huasdorff距離定義為兩組點集之間的距離，是描述兩組點集之間相似程度的一種量度。

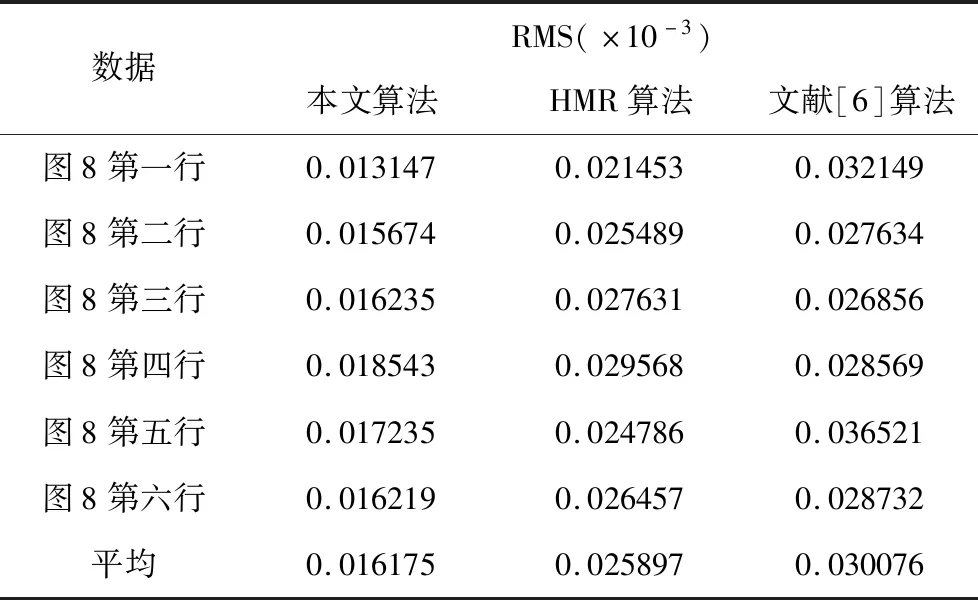
表1 定量分析表

對比結果如表1所示。從表1的對比結果分析，無論是踢腿、半蹲還是舉手等動作，本文方

法在誤差表現上都優于其它兩種方法。綜上所述，本文算法能夠有效利用Kinect三維關節點的約束對人體模型參數進行求解，并且得到相對優于HMR和文獻[6]算法的結果。

5 結論

本文通過總結和分析基于模型的人體姿態估計算法的研究現狀，發現了目前算法存在精度有限、信息缺失等問題。針對這些問題，本文提出將Kinect三維關節點擬合到SMPL模型上，來恢復更真實的人體網格模型的方法。

該算法具有以下三個優勢。一，采用Kinect相機采集數據，快速便捷；二，通過Kinect得到的人體三維信息，彌補了由二維圖像映射到三維姿態時的缺失信息，減少了姿態估計時的誤差；三，相較于從彩色圖像擬合人體模型的方法，本文利用更能反映人體真實姿態的三維人體骨架，提取的特征維度更高，能夠更詳細的描述目標信息。實驗結果表明本文方法較HMR方法在RMS誤差上平均減小了37.5%，較文獻[6]方法平均減小了46.2%，綜上，本文算法通過人體三維信息的補足和約束，提高了姿態估計的精度，得到了更真實的人體模型。

文中使用的 SMPL 模型是不包含臉部與手部的模型，在后續的工作當中，可以考慮使用最新的人體形變模型[15]，來進行更為全面(包含臉、手等多部位)的人體姿態建模，并結合光照和人體紋理等信息來構建出更為逼真的人體模型。