翼傘系統動力學建模與分段歸航設計

劉佳璽，劉黨輝，刁俊昌

(1. 航天工程大學研究生院，北京 101416；2. 航天工程大學宇航科學與技術系，北京 101416；3. 31700部隊，遼寧 遼陽 111000)

1 引言

航天運載器的精確定點以及無損回收一直是各國學者不斷探索研究并急需解決的技術難題[1]，20世紀60年代，法國人賈爾伯特(JALBERT)首次提出了“沖壓翼傘”的概念，基于沖壓翼傘的空投系統以及運載器回收系統開始進入人們的視野，通過對翼傘系統合理的動力學建模以及歸航設計，可以大幅度提高空投系統以及運載器回收系統的精確性[2]。

在1978-1984年間，Goodrick先后建立翼傘系統縱向平面的3DOF模型以及6DOF[3]模型開始，國內外學者對翼傘系統的動力學建模進行了較多的研究，翼傘系統的8DOF[4]、9DOF[5]、12DOF[6]動力學模型相繼建立。6DOF模型是將翼傘與載荷看做剛性連接，系統在整個歸航階段主要以滑翔為主。更高自由度的動力學模型主要用于分析物、傘系統間的相對運動特性，其中8DOF與9DOF模型是將傘體和回收物間通過長度恒定的吊帶相連，而12DOF模型更是考慮到了吊帶的彈性形變，這對詳細分析翼傘系統歸航中突風作用、雀降操縱以及系統設計參數優化等提供了更精確的理論依據。本文主要研究的是翼傘系統的歸航設計，而歸航設計旨在分析系統質心的運動規律，了解飛行軌跡以及飛行性能。6DOF模型可以直觀清晰的描述系統的基本運動特性，而且相對較為簡單，而更高自由度的模型建立較為復雜，不利于歸航過程中的軌跡以及系統控制器的優化。只有當需要獲得更多信息，并進一步了解系統各組成部分--傘體以及回收物之間的相互影響時，才需要建立更高自由度的動力學模型。所以本文采用翼傘系統的6DOF模型進行歸航設計。

對于翼傘系統而言，軌跡規劃不僅要實現安全地著陸，更要保證著陸精度，以及能量控制在允許范圍之內等多項要求。當前，翼傘系統軌跡規劃的研究方法大致可分為三種：簡單歸航法[10]，最優控制歸航法[11]以及分段歸航法[12]。相比于前兩者，分段歸航操縱簡單，魯棒性強，可以實現逆風對準，在實際工程中應用越來越廣泛。

2 翼傘系統六自由度動力學模型

2.1 翼傘系統的附加質量

由流體力學概念可知：附加質量是物體在流體中做加速運動時產生的，當物體運動速度大，而加速度和尺寸小時，則運動的阻力主要由物體粘性摩擦引起；而當速度很小，加速度和尺寸很大時，運動的阻力主要產生于克服周圍流體的慣性阻力。降落傘的開傘過程屬于后者，其次降落傘通常在空氣中運動，傘的平均密度與空氣的密度相當，附加質量與傘體本身質量處于同一量級，因此在計算降落傘的開傘動載以及運動分析中必須考慮附加質量。

附加質量和附加質量慣性矩是個矢量，不同于物體質量是個標量，它與物體的運動方向有關。根據流體力學理論，在六自由度運動方程中，附加質量和附加質量慣性矩表示為6×6的矩陣，共36個分量[2]。由于附加質量具有對稱性mik=mki，所以其中只有21個獨立分量，其中m11，m12，m13，m22，m23，m33稱附加質量，m44，m45，m46，m55，m56，m66稱附加質量慣性矩。而對于具有軸對稱的降落傘來說

m12=m13=m23=m45=m46=m56=0

附加質量分量只存在于m11、m22、m33，附加質量慣性矩只存在于m44、m55、m66，其表達形式為[2]

本文采用Barrows提供的附加質量矩陣形式，對于平直翼而言，其計算公式如下[7]

由于翼傘展向是圓弧形，真正的附加質量計算公式要根據拱高以及展向彎曲弧度等參數進行修正，如圖1所示。由參考文獻[7]可知，平直翼與拱形翼在數值精度上差異小于2%，本文為計算方便，直接應用平直翼的附加質量計算公式以簡化計算。

圖1 翼傘平直翼與拱形翼示意圖

2.2 翼傘系統六自由度模型

2.2.1 基本假設

1)翼傘是展向對稱的，傘衣完全張滿后具有固定的形狀(后緣的下偏操縱除外)；

2)載荷所受阻力遠大于升力，對其升力忽略不計；

3)載荷與翼傘剛性連接成為一個整體；

4)傘衣的壓心和質心重合，位于弦向距前緣1/4處；

2.2.2 翼傘系統氣動力與力矩分析

對于翼傘氣動力的計算，最可靠的方式還是飛行試驗，但是由于飛行試驗耗資巨大并不能滿足日常學術研究的需求，而對于風洞試驗，也因翼傘的柔性特質而難以實現。近年來，隨著CFD技術的廣泛應用，通過數值計算以及計算機仿真獲得翼傘氣動力參數的方法發展迅猛。為分析翼傘單側下拉的轉彎運動，目前廣泛采用的是Goodrick的分片處理的工程方法，國防科技大學的熊菁[4]采用的是試驗數據以及工程分片處理相結合的方法來計算翼傘的氣動力以及氣動力矩。對于本文，對翼傘系統的合力Faero以及合力矩Maero進行分解并逐一計算，最終得到氣動力以及力矩的表達式

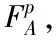
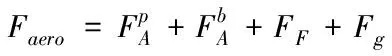
(1)

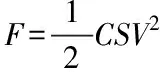
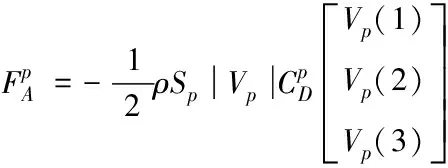
(2)

2)在計算作用在傘體上的氣動力時，需要用升力減去阻力，其表達式如下

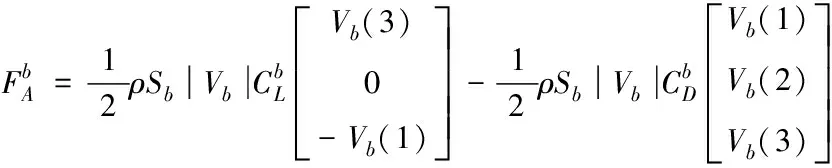
(3)

3)在計算附加質量產生的力矢量時，根據1.1得到的翼傘系統附加質量，可以得到翼傘系統附加質量產生的力矢量表達式為：

FF=-mFaC

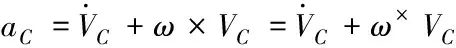
(4)

4)在計算系統所受重力時，需要將慣性坐標系轉換到體坐標系上，又因為重力加速度g只作用于慣性系的Z軸，所以重力的表達式為：

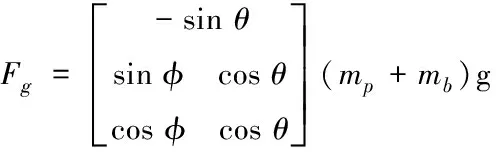
(5)

接著對翼傘系統的力矩關系進行分析，因為系統所受重力不可控，可以不考慮重力產生的力矩，只計算氣動力矩(MA)以及附加質量作用力所產生的力矩(MF)，所以翼傘系統合力矩的表達式為

Maero=MA+MF

(6)

1)在計算翼傘系統的氣動力矩時，可將氣動力矩分解為滾轉力矩，俯仰力矩，以及偏航力矩，其表達式可由參考文獻[8]給出

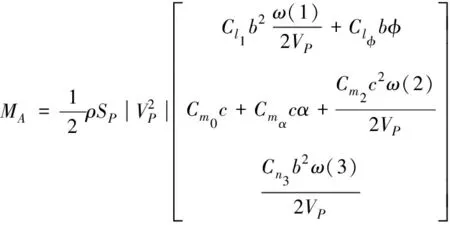
(7)

2)在計算附加質量的作用力矩時，根據2.1得到的附加質量慣性矩，可以得到附加質量作用力矩的表達式為

(8)

2.2.3 翼傘系統動力學方程

求翼傘系統動力學方程時，首先根據2.2.2推導的翼傘系統所受合力以及合力矩的分量，得到力與力矩的平衡方程。因為翼傘在左右下拉后緣進行轉彎或減速(雀降)運動時會產生襟翼偏轉δa和δs，從而對氣動力和氣動力矩產生影響，所以需要加上修正量ΔFA和ΔMA則翼傘系統力與力矩的平衡方程為

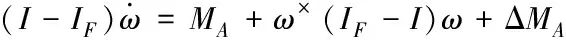
(9)

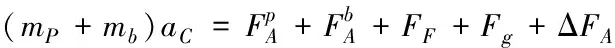
(10)

其中，I為翼傘系統傘體和載荷轉動慣量之和。

接下來就可以建立含附加質量的翼傘系統六自由度動力學方程

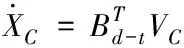
(11)

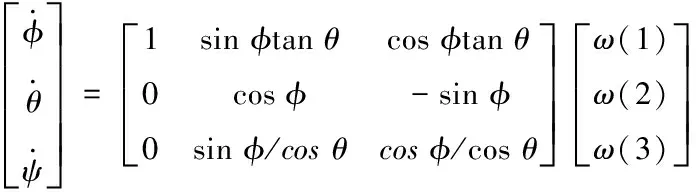
(12)

通過翼傘系統力與力矩的平衡方程對VC與ω進行迭代求解，將其帶入翼傘系統六自由度動力學方程中，便可以實時求出模型的六個狀態量，從而得到翼傘系統在整個歸航過程中的運動軌跡，這樣對了解翼傘系統的運動特性有非常重要的參考作用。

3 翼傘系統分段歸航設計

3.1 分段歸航方案

分段歸航的軌跡大致可以分為三段：向心飛行-目標接近段；盤旋削高-能量消耗段；逆風對準-雀降著陸段，如圖2所示采取分段歸航極大簡化了歸航過程中系統的操縱過程，并且有利于實現各個參數的優化。

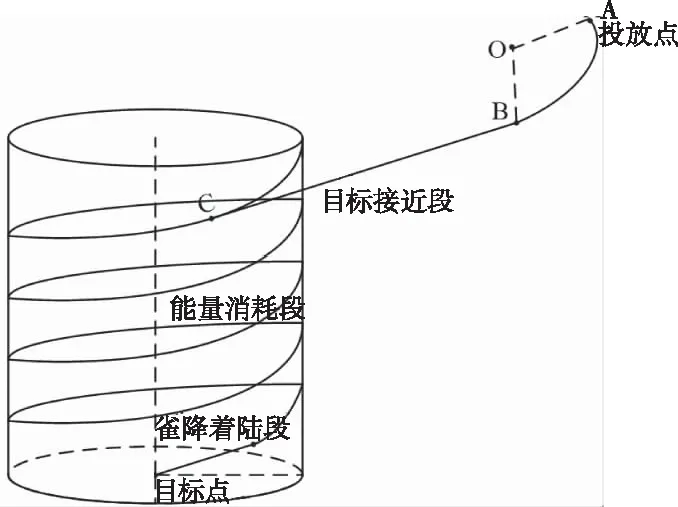
圖2 翼傘系統分段歸航過程示意圖

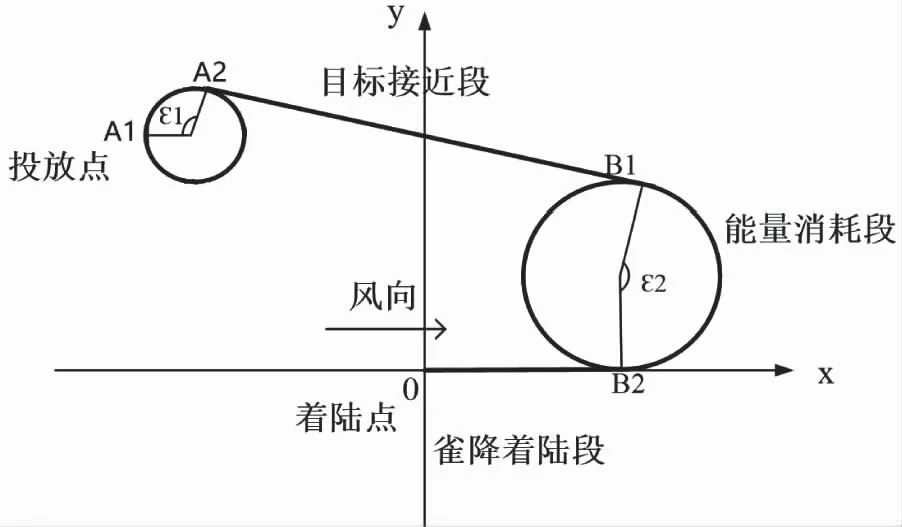
圖3 傳統分段歸航方案

如圖3所示，傳統的分段歸航方案是在離目標區較近的下風區做轉彎運動不斷消耗高度，直到滿足最終條件時逆風雀降著陸，這樣的歸航模式簡單，不會出現復雜的操縱變換，但是對于整個歸航任務來說，必須盡可能控制著陸能量，以防在緊急情況發生時著陸精度有所保證。傳統的分段歸航方案轉彎半徑較小，對于翼傘系統而言，轉彎半徑越小，翼傘后緣所需的下拉操縱量越大，所需要消耗的能量也就越多，而且過小的轉彎半徑需要極大的轉彎角速率，在轉彎初期會造成物傘系統之間較大的相對運動，不利于系統的穩定性。

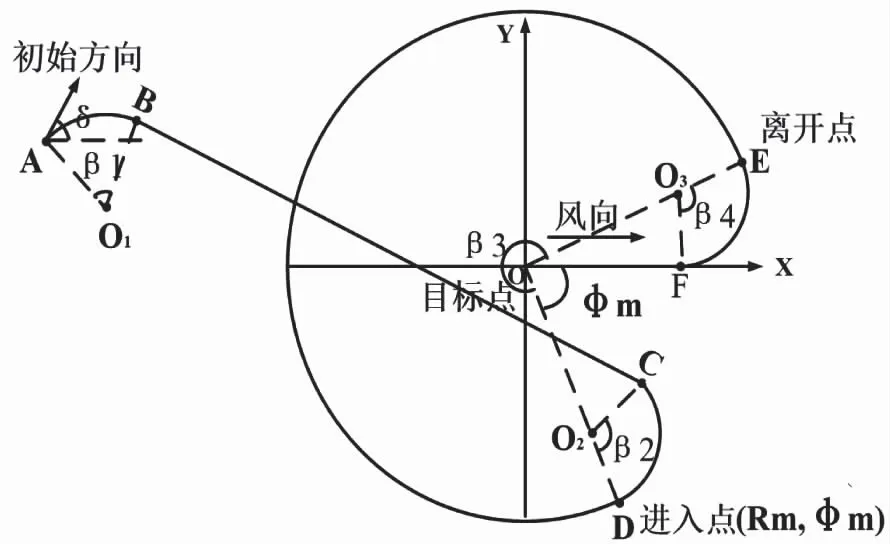
圖4 新型分段歸航方案

在新的歸航方案中，如圖4所示為了減小能量損耗，主要以直線以及大圓弧為運動形式，只有在兩者銜接處采用小圓弧過渡，在投放點高度合適的情況下，可以通過改變圓弧大小來調節軌跡，確保了回收精度。

3.2 軌跡計算

如圖4所示，A點為初始點，δ為初始飛行方向角(初始運動方向與X軸正向的夾角)，B點到C點為目標接近段做滑翔運動。D點到E點為能量消耗段，F點到O點為雀降著陸段做減速運動，β1,β2,β4為過渡段的圓弧角，其轉彎半徑為Rmin,β3為能量消耗段的圓弧角。

以坐標原點作為目標點，歸航軌跡隨著初始點的變化而變化，設整個歸航過程中翼傘系統的滑翔比保持恒定為k，由以上分析可以得到系統歸航的目標函數：

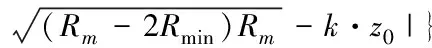
(13)

該目標函數反應的是設計軌跡的水平飛行距離與初始高度所對應的水平飛行距離差的絕對值。

4 仿真分析

4.1 翼傘系統基本運動特性分析

翼傘的基本運動特性包括無下拉的滑翔運動，單側下拉的轉彎運動以及雙側下拉的減速運動(先不考慮雀降)。

設置模型參數，初始投放高度為(0，0，3000)m，初始速度為(14，0，5)m/s，系統的初始角速度、歐拉角等都設置為 0，翼傘系統自身的結構以及氣動參數可由參考文獻[8]得到，在運動過程中的操縱見表1。

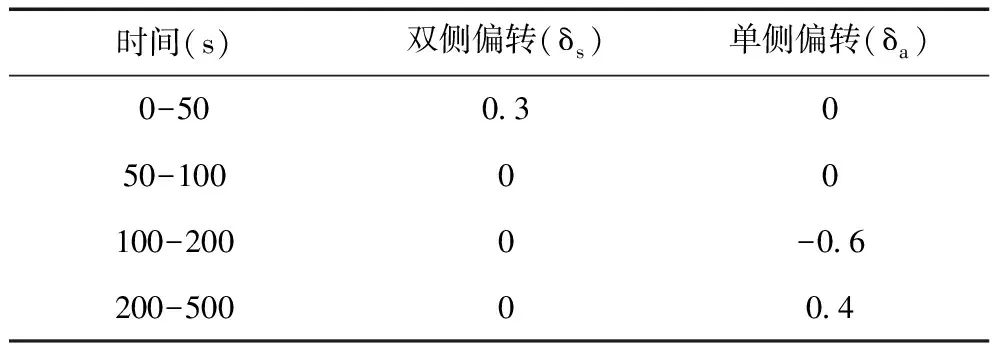
表1 翼傘系統操縱方式

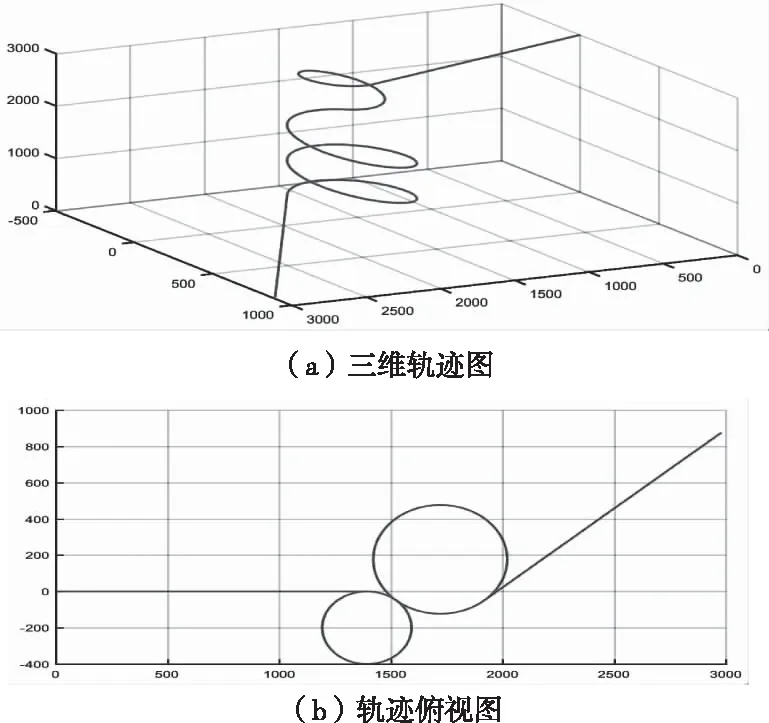
圖5 翼傘系統運動軌跡示意圖

隨著操縱方式的變化，翼傘系統的三個姿態角也會隨之變化，如圖6所示。

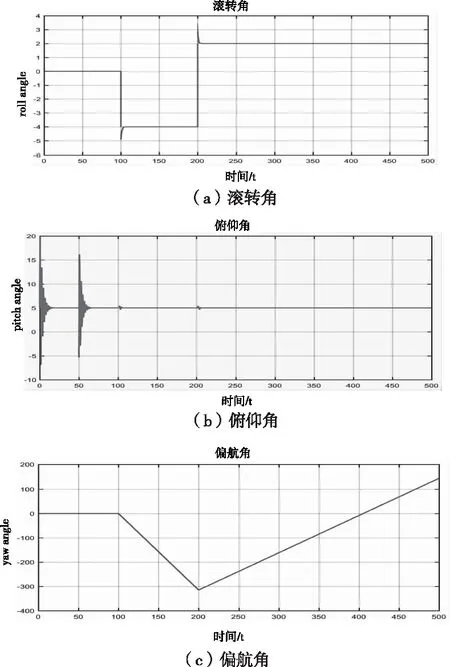
圖6 翼傘系統姿態角變化曲線

對圖形分析可以得到，前50s以及50s到100s之間均是直線滑翔運動，此時滾轉角與偏航角不發生變化；俯仰角在每次改變操縱時會發生一定范圍的波動最終趨于某一恒定值。

在100s到200s之間以及200s之后均做單側下拉的轉彎運動，其中轉彎方向由下拉量的正負決定，轉彎半徑的大小由下拉量的絕對值決定，且絕對值越大，轉彎半徑越小。滾轉角與翼傘的運動狀態相關，且轉彎半徑越大，滾轉角的絕對值越大；俯仰角會發生小范圍波動最終繼續趨于穩定，單側下拉的操縱對俯仰角產生的波動不大；偏航角根據轉彎方向的不同按照不同的速率恒定變化。

4.2 翼傘系統分段歸航軌跡優化

設置初始條件：A(1000，-400，1260)，初始方向角為60度，最小轉彎半徑為120m，Rm∈(400，600)，滑翔比k=2.8，水平速度為18.4m/s，過渡段的圓弧角小于180度。

利用幾何關系求最優軌跡可以理解為參數優化的問題，可利用計算機智能算法仿真解決。利用遺傳算法設置初始種群的大小為100，交叉概率為0.7，變異概率為0.2，最大迭代次數為1000，在滿足約束條件下利用matlab遺傳算法工具箱的ga函數迭代求解出目標函數的最優值，最終得到整個歸航過程所需的所有幾何參數如下

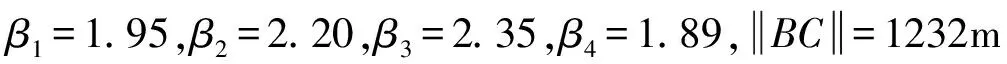
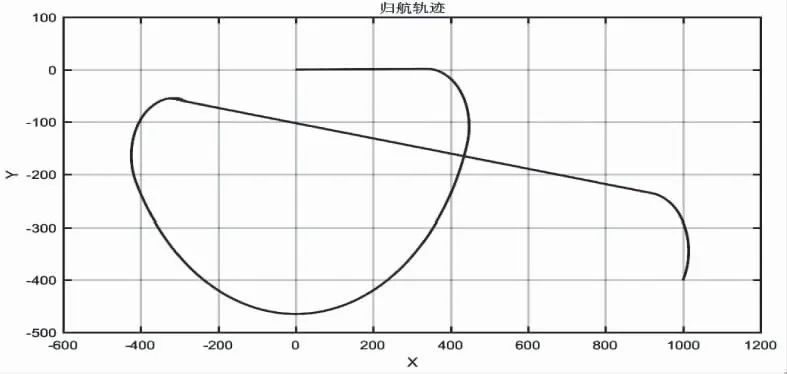
圖7 新型分段歸航方案軌跡俯視圖

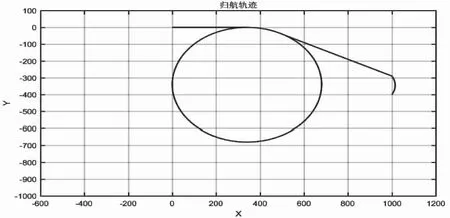
圖8 傳統分段歸航方案軌跡俯視圖

由翼傘系統動力學模型可得翼傘單側下偏控制量與轉彎半徑的關系見表2．

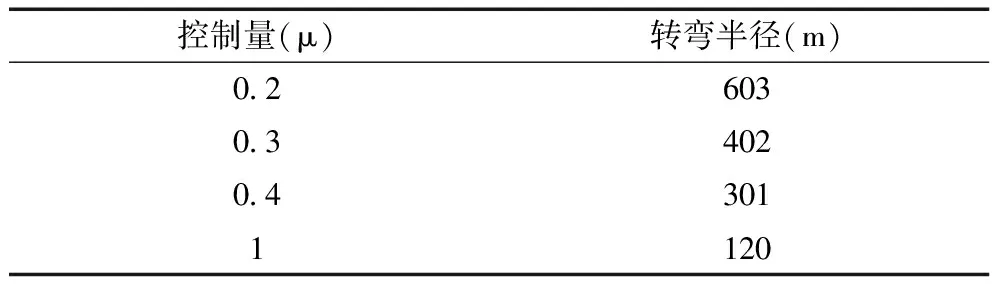
表2 翼傘下偏控制量與轉彎半徑關系表

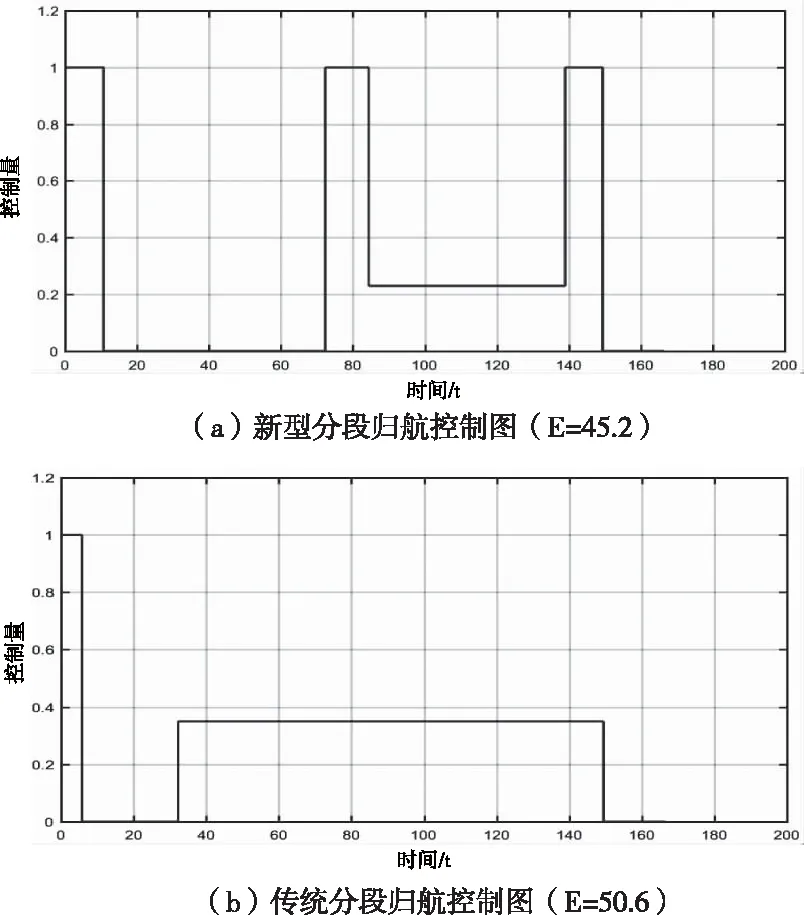
圖9 分段歸航方案控制圖

經計算，相比于傳統分段歸航方案，新型分段歸航方案所耗能量小，轉彎半徑大，對系統的能量控制以及穩定性更具有優勢。

5 總結

本文對翼傘系統的六自由度動力學模型做了詳細的推導，對其中附加質量，氣動力以及氣動力矩的計算方程做了歸納與總結。其次，利用分段歸航軌跡的幾何特性確定了各段的參數，并利用遺傳算法對各參數進行了優化，得到了在滿足投放高度的情況下任意投放點到目標點的軌跡曲線方程。最后對傳統分段歸航方案以及新型分段歸航方案做出了對比，得到新型歸航方案對翼傘系統歸航過程的能量控制以及穩定性有更強的優勢。