我的“勾股定理”證明法

文／河南省鶴壁市致遠中小學 李雙陽

勾股定理占據了幾何學的半壁江山。當我剛接觸勾股定理時，就被那簡單的公式迷住了。

那天，數學老師讓我們根據導學案來探究勾股定理的證明方法。導學案上有兩個圖形，分別是“趙爽弦圖”和“畢達哥拉斯證明圖”。通過觀察，我隱約感覺它們之間有著某種聯系。因為數學老師一直教導我們，對于數學一定要有鉆研精神，所以我試著把兩個圖形比較了一下，發現當直角三角形全等的時候，“趙爽弦圖”正好可以和“畢達哥拉斯證明圖”中間的正方形重合，于是我就把兩個圖拼到了一起，得到了一個新的圖形（如圖1）。看著這個熟悉又陌生的圖形，我不禁想，這個圖是不是也能證明勾股定理呢？

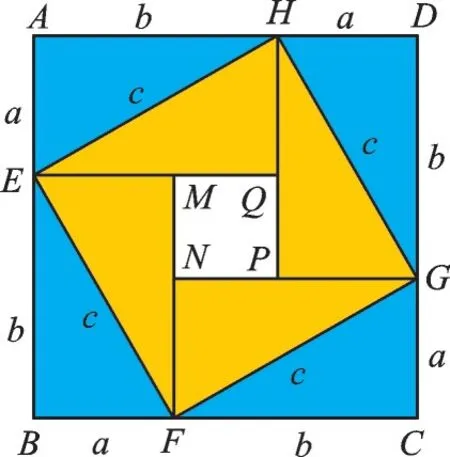
圖1

“趙爽弦圖”和“畢達哥拉斯證明法”都是根據面積關系列出等式而證明的，所以我猜想，這個新圖形應該也可以根據面積來證明。我發現，把每個圖形的面積都表示出來比較麻煩，但是結合“趙爽弦圖”和“畢達哥拉斯證明法”中的面積表示，就會簡單很多。

下面是我的證明過程。

如圖1，正方形ABCD由八個全等的直角三角形和一個正方形MNPQ構成，其中，AE=a，BE=b，EH=c。根據“畢達哥拉斯證法”可知，SABCD=（a+b）2，而由“趙爽弦圖”可知，SMNPQ=（b-a）2，SEFGH=c2。在圖1中，可得SABCD+SMNPQ=2SEFGH，即（a+b）2+（b-a）2=2c2，整理得a2+b2=c2，則證得勾股定理。

通過本次對勾股定理的探索和證明，我受益匪淺，也更加喜歡數學了。數學，真的是一門神奇的學科。一個勾股定理就有這么大魅力，數學中還會有多少美妙的東西等著我們去探索發現呢？

教師點評

小作者善于觀察和思考，能在已有知識的基礎上，勇于創新，發現不同于我們常用的證明方法，充分體現了數學學習中的創造力，很了不起！