基于集成聚類和XGBoost 的短期光伏發電功率預測

常俊曉，金之榆，盧 姬，吳思圓

（1.國網浙江省電力有限公司臺州供電公司，浙江 臺州 318000；2.國網浙江省電力有限公司臨海市供電公司，浙江 臨海 317000）

0 引言

為實現能源轉型升級，達成“雙碳”目標，大力發展光伏產業已經確定為國家既定國策，光伏發電將迎來黃金機遇期。2020 年，光伏新增裝機48.2 GW，棄光量達52.6 億kWh。準確預測光伏發電功率對充分挖掘源網荷儲調節潛力，提升消納利用率具有重要意義[1]。

光伏發電功率具有較大的波動性和隨機性，其預測方法主要分為物理法和統計法。物理法主要通過天氣預報、衛星遙感測量和地面測量設備來獲得預測所需數據，對設備要求較高；統計法是一種數據驅動的方法，根據歷史數據提取特征來預測未來的光伏發電功率，成本低且適應性強，得到廣泛應用[2]。當氣象類型相同時，光伏發電具有較高的相似性，發電功率大小與各種氣象特征有著密切的聯系[3-4]。因此，對氣象數據進行聚類分析，針對不同氣象類型的數據，選用相似日樣本數據進行預測可以有效提高預測精度[5-6]。但目前聚類方法存在最佳聚類數難以確定和初始聚類中心隨機選擇導致聚類結果不穩定的缺點。文獻[7]針對K-means 聚類算法（K-均值聚類算法）無法聚類確定最佳聚類數的缺點，提出了自適應K-means 聚類算法，并結合了LSTM（長短時記憶網絡）算法，在提高預測精度上取得了較好的效果，但是并沒有解決K-means 聚類算法初始聚類中心隨機選擇的缺點，隨著數據集規模的增大容易導致聚類結果不穩定；文獻[8]通過減法聚類確定K-means 聚類算法的最佳聚類數，通過分散選取聚類中心的方法避免聚類結果陷入局部最優，但降低了聚類速率。在預測模型方面，傳統的GBDT（梯度提升樹）算法存在預測結構簡單、預測精度低的缺點。XGBoost（極端梯度提升）算法[9]是一種基于決策樹的集成學習算法，使用梯度上升框架，在數據分類以及回歸處理方面有著顯著的效果，廣泛應用于天文學、氣象、電力等領域中的預測分析。文獻[10-11]中使用XGBoost 算法建立了光伏發電功率預測模型，實驗證明該算法具有較好的實用性和可行性，但沒有充分考慮天氣對光伏發電功率預測精度的影響。

基于上述分析，本文提出基于集成聚類和XGBoost 的短期光伏發電功率預測方法。首先，采用Mean-shift（均值漂移算法）、凝聚層次聚類算法確定初始聚類中心，結合DBI（戴維森堡丁指數）確定最佳聚類數，得到自動確定最佳聚類數且聚類結果穩定的集成聚類算法；然后，采用集成聚類算法對數據進行聚類，得到不同氣象類型的預測樣本集；最后，對各種天氣類型的訓練集數據分別采用參數少、計算效率高的XGBoost 集成學習算法訓練模型，結合訓練完成的模型分別對晴天、多云、陰雨天3 種天氣類型的測試集數據進行算例分析，驗證了所提組合預測算法可以得到更加精確的預測結果。

1 XGBoost 預測算法原理

相比于傳統的GBDT 算法，XGBoost 具有更強的擴展性，而且可以同時使用一階和二階導數，能更好地獲得代價函數的信息量，提高預測結果的精確度；且XGBoost 算法使用類似隨機森林的策略對數據進行采樣，不需要重復調取數據，這使得計算效率大大提高[12]。

設有n 個樣本和m 個特征的數據集D=（xi，yi），其中，yi∈R。提升樹模型中構建了K 個樹，表示為F={f1（x），f2（x），…，fk（x）}，k∈K；目標函數表達式如下：

式中：fk為XGBoost 中的一個CART 回歸樹函數；表示預測值；yi為真實值。

經過t 次迭代后將XGBoost 擬合殘差代入式（1），并對其進行二階泰勒展開，得到新的目標函數：

為了學習模型中的函數集合，XGBoost 模型最小化正則化目標如下：

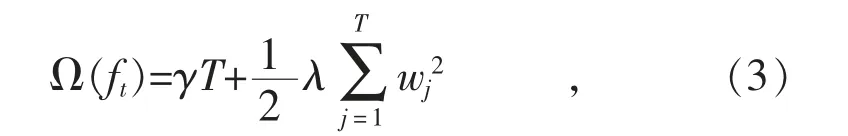
式中：fk（x）=wq（x），q（x）為輸入測試集樣本決策樹葉子結點編號的映射，表征決策樹結構；w 為決策樹的輸出值；設每個樹的節點樣本集合為IJ={i q（xi）=j}；T 為每個回歸樹的葉子節點數；γ 為葉子節點個數；λ 為正則化項懲罰系數。

將式（3）和式（2）進行組合可得XGBoost 基于加法方式的迭代函數：

假設式（4）中q（xi）的值固定，求導得到目標函數的極值點，代入式（4）可得最終目標函數：

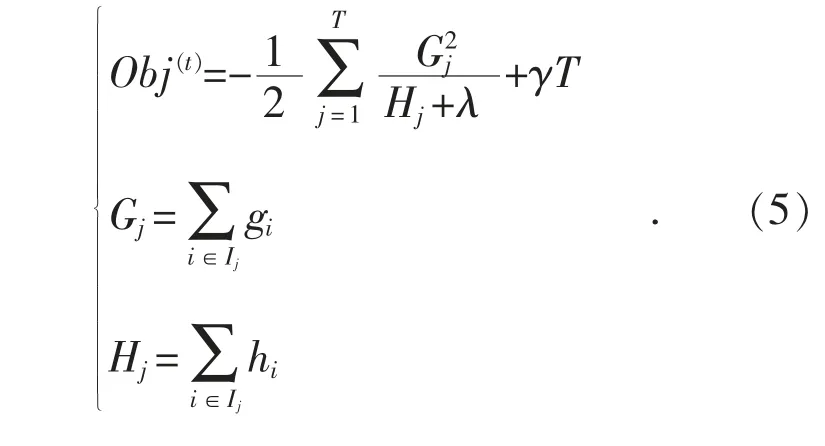
Obj（t）表示選定樹結構增益損失的最大值，其數值越小表示模型精度越高，在模型訓練過程中XGBoost 算法利用誤差函數不斷優化模型。

2 集成聚類和XGBoost 的組合預測框架

2.1 數據預處理

不同的氣象特征數據具有不同的數量級，對于聚類算法來說，將氣象特征數據集中到一個范圍內可以提升模型的收斂速度，得到更好的聚類結果。影響光伏發電功率的氣象特征有溫度、壓強、濕度、輻照度和實發輻照度[13]，采用最大-最小歸一化方法預處理數據，得到式（6）：

式中：xmax，xmin分別為樣本中特征最大值和最小值；xnew為歸一化后的樣本x。

將實驗數據集表示為H，數據集中的日氣象特征表示為：

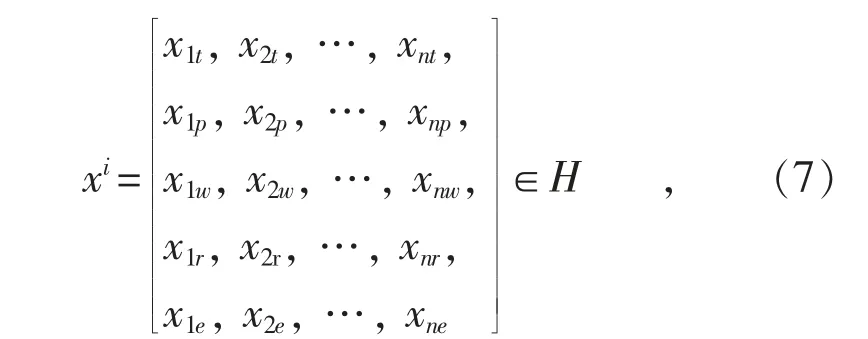
式中：xi表示第i天的氣象特性樣本；xnt，xnp，xnw，xnr，xne分別表示第n 時刻的溫度、壓強、濕度、輻照度和實發輻照度。

2.2 集成聚類算法

K-means 聚類算法[14]無法確定最佳聚類數，且初始聚類中心選擇具有隨機性，導致聚類結果不穩定。為此，本文設計的集成聚類算法，其基本思路是使用Mean-shift 密度聚類確定初始聚類中心，通過凝聚層次聚類和聚類結果評價指標確定最佳聚類數。具體過程：首先在經過數據預處理的數據集上進行Mean-shift 密度聚類，對得到的聚類中心使用凝聚層次聚類算法進行組合；再根據聚類結果評價指標，將相似的聚類中心合并，得到新的聚類中心和聚類數；最后將新的聚類中心和聚類數分別作為K-means 聚類算法的初始聚類中心和最終聚類數對數據集再次進行聚類，得到最終的聚類結果。

2.2.1 Mean-shift 聚類

Mean-shift 算法是Fukunaga 團隊提出的一種無參數密度估計算法，又稱均值漂移算法。由于這種算法可以應用在任意形狀數據集的密度估計中，因而在數據聚類、圖像追蹤中應用廣泛。它通過計算當前樣本的均值偏差來不斷更新類簇的中心點，直到類簇中心收斂到概率密度極大值處，并且不需要提前設置聚類數。用Mean-shift算法對電力負荷曲線進行初步聚類可以在全局范圍內確定聚類中心，避免聚類結果陷入局部最優。

2.2.2 凝聚層次聚類

在集成聚類算法中，凝聚層次聚類可以看作對K-means 聚類算法初始聚類中心的預處理步驟，它對Mean-shift 算法選出的聚類中心進行組合。為了確定最佳聚類數，解決K-means 聚類算法受初始聚類中心影響較大的問題，采用聚類質量高、結果穩定的凝聚層次聚類算法，可以輸出較好且穩定的聚類中心組合，從而使得K-means算法聚類結果更優。

集成聚類算法的具體步驟如下：

1）通過Mean-shift 算法對數據集進行聚類處理，得到S 個聚類中心。

2）采用凝聚層次聚類對CA的聚類中心進行合并，合并結束條件為“是否達到事先給定的聚類數目”，需要通過聚類有效性指標來確定最佳的聚類數目kbest，得到合并后的聚類中心。

3）將kbest以及聚類中心作為K-means 聚類算法的輸入參數和初始聚類中心對數據集進行聚類，輸出聚類結果。

聚類流程如圖1 所示。

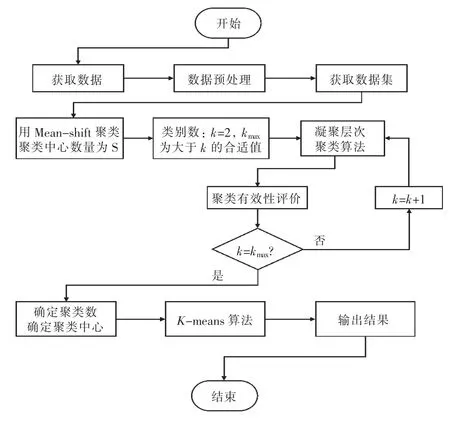
圖1 集成聚類流程

2.3 組合算法結構

本文采用集成聚類和XGBoost 組合預測算法對短期光伏發電功率進行預測，具體流程如圖2所示。

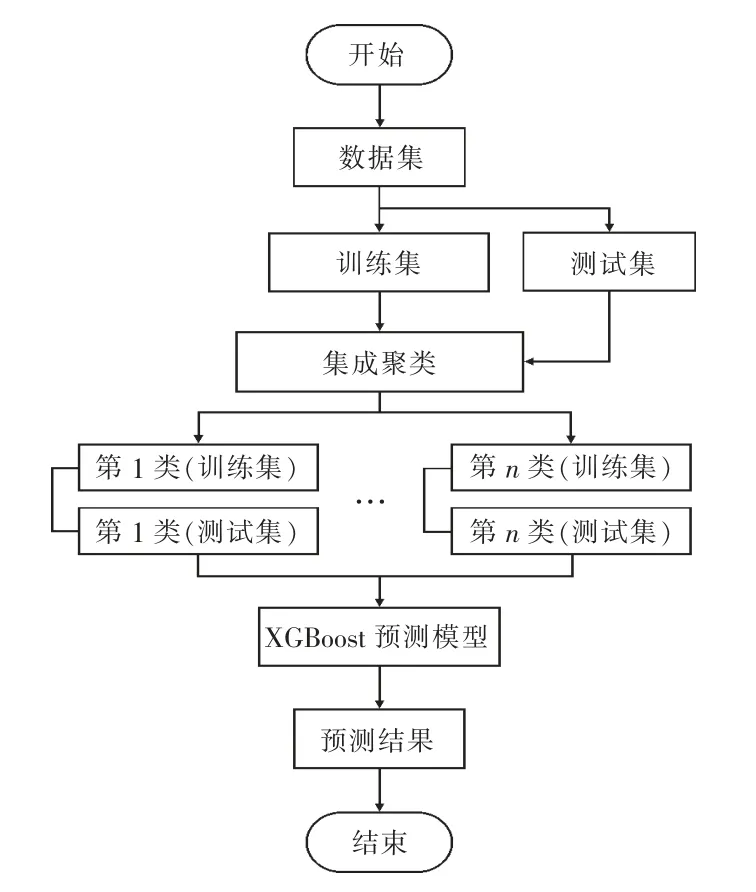
圖2 組合預測流程

1）獲取功率數據與氣象數據樣本，選取溫度、壓強、濕度、輻照度和實發輻照度為氣象特征分量。

2）采用集成聚類對訓練集氣象數據聚類處理，得到不同氣象類型的預測樣本集。

3）預測模型初始化，并對XGBoost 算法的主要參數尋優，直至訓練網格模型最優；然后利用不同氣象類型的訓練集樣本分別訓練XGBoost 算法預測模型。

4）通過計算測試集樣本與聚類中心的距離來確定預測樣本的氣象類型，輸入對應氣象類型的預測模型中得到預測結果。

3 實驗結果與分析

本文實驗數據來自某市一個三相并網光伏發電系統，數據采集天數為600 天，日氣象特征向量為每隔15 min 采集一次的溫度、壓強、濕度、輻照度和實發輻照度，共600 個樣本。考慮到光伏發電的特殊性，將預測時間區間設定為6:00—18:00。

3.1 聚類結果分析

以所有樣本的溫度、壓強、濕度、輻照度和實發輻照度作為輸入，分別采用K-means 聚類算法和集成聚類算法進行聚類。考慮到K-means 聚類算法的不穩定性，對數據進行多次（20 次）聚類，取最優值，其中輸出類簇的設置范圍為[2，10]，采用DBI 評價其聚類質量，計算公式如下：

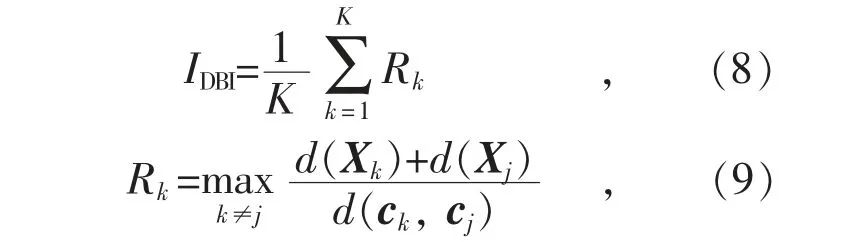
式中：d（Xk）與d（Xj）分別表示類簇k，j 中的每個樣本到類簇中心的平均距離；d（ck，cj）表示類簇k，j 的類簇中心之間的距離。IDBI的數值越小，表示聚類結果的質量越好。

當k 取不同值時IDBI如圖3 所示，可以看出，當k 取3 時，IDBI最小為1.59，此時聚類效果最佳。使用集成聚類處理相同數據集，聚類結果如表1 所示，經對比可以看出，集成聚類算法可以自動得到最佳聚類數，且IDBI為1.42，比K-means的聚類效果更好。因此，采用集成聚類算法不僅可以自動得到最佳聚類數，同時由于避免了初始聚類中心的隨機選擇，還能得到更好的聚類效果。

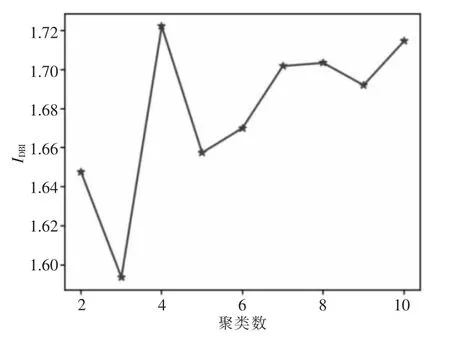
圖3 K-means 不同聚類數的IDBI

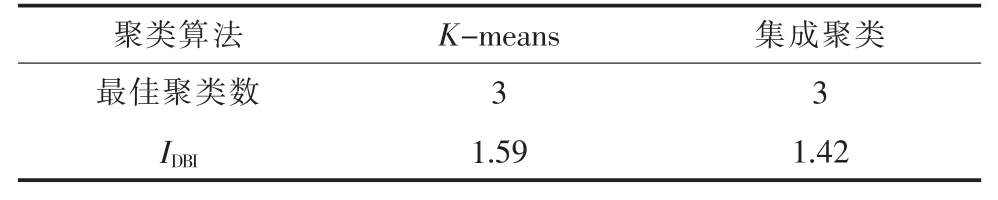
表1 聚類結果

3.2 預測結果分析

選取3 個不同天氣典型日，分別采用3 種方法進行預測：方法1，集成聚類與GBDT 相結合；方法2，K-means 與XGBoost 相結合；方法3，集成聚類與XGBoost 相結合。

為了確保參數設置最優，本文使用Gridsearch網格搜索法對2 種算法的主要參數尋優進行。XGBoost 模型參數：learning_rate（學習率）設置為0.1，max_depth（樹的深度）設置為4，n_estimators（樹的棵樹）設置為45，min_child_weight（最小葉子權重）設置為4，其余參數設置為默認值；GBDT 模型參數：n_estimator（最大迭代次數）設置為52，learning_rate（學習率）設置為0.3，loss（損失函數）設置為“huber”，其余參數設置為默認值。

為了評價不同方案的預測效果，本文采用MAPE（平均絕對誤差）和RMSE（均方根誤差）分別評價預測結果，2 種評價指標的數值越小，表示預測結果越接近真實值。

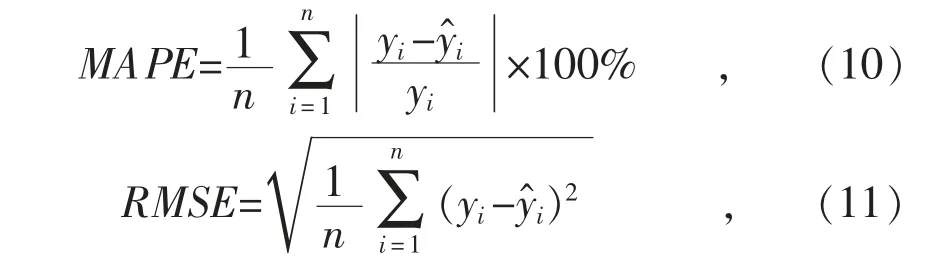
式中：n 為預測值數量；yi和分別為負荷真實值和預測值。

3 種方法的預測結果如表2 所示。

表2 3 種方法預測結果

1）晴天預測結果。

由圖4 中光伏功率曲線可以看出：晴天光伏發電功率比較穩定，使用3 種方法都可以得到較好的預測結果，同時結合表2 中的MAPE 值可知，集成聚類與XGBoost 組合算法的預測結果誤差最小。

圖4 晴天預測結果

2）多云天預測結果。

由圖5 中預測曲線可以看出：多云天氣的光伏發電功率波動較大，方法1 的預測結果與實際波動曲線相差較大，在13:00—15:00 的預測值偏差非常明顯；但方法2 和方法3 的預測結果相對準確，更加接近真實值，結合表2 中的MAPE 值可以看出，方法3 的預測結果最準確。

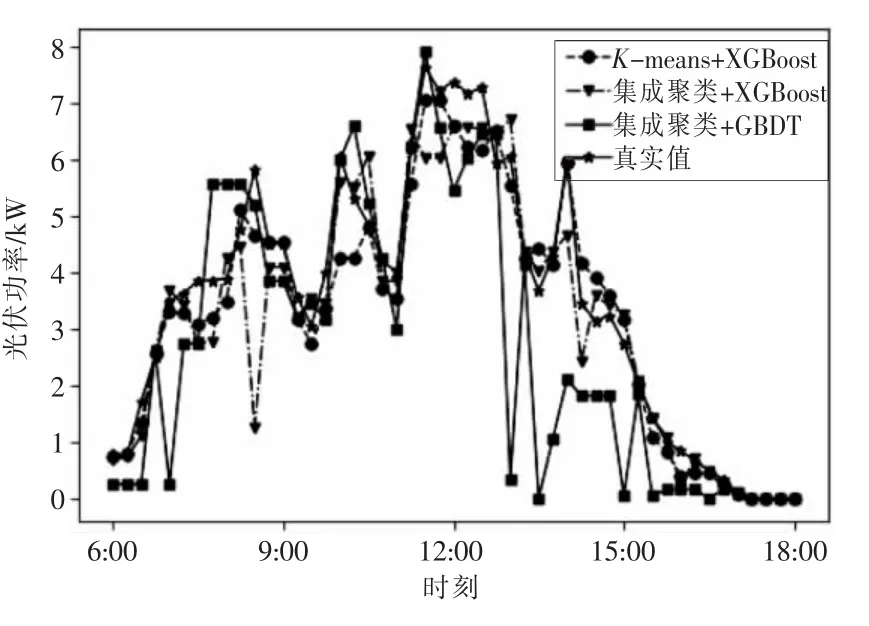
圖5 多云天預測結果

3）陰雨天預測結果。

由圖6 中預測曲線可以看出：3 種類型天氣中，陰雨天的光伏發電功率最小，且波動最為明顯，這導致方法1 的預測結果與真實曲線差距較大，特別是12:00—16:00 的預測值偏離真實值最多，與真實曲線不符；方法2 預測功率值與真實曲線相差較小；方法3 的波動情況比方法2 更加接近真實曲線，結合表2 的MAPE 值可以看出，本文提出的集成聚類與XGBoost 組合的算法更加適應功率的波動，預測結果更準確。

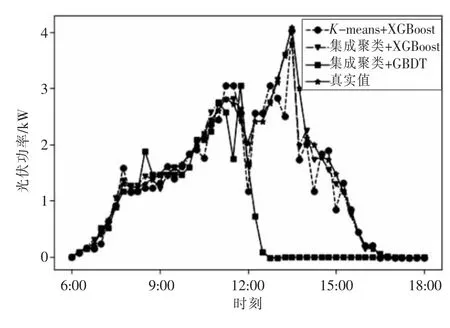
圖6 陰雨天預測結果

對比不同天氣狀況下的預測結果發現，GBDT算法雖然在晴天的預測結果較好，但是無法應對較為波動的天氣情況，當天氣情況發生波動時，預測結果誤差會迅速加大，無法像XGBoost 算法一樣適應天氣波動。經過集成的K-means 聚類算法比原始K-means 聚類算法的聚類結果更穩定，聚類質量更高，并且可以自動得到最佳聚類數，還能通過提供更準確的聚類樣本提高XGBoost 算法的預測精度。

4 結論

通過實例分析可以證明，本文所提的預測方法具有以下優勢：

1）結合了Mean-shift 算法、凝聚層次算法和K-means 聚類算法的集成聚類算法解決了Kmeans 聚類算法無法確定最佳聚類數和隨機選定初始聚類中心的問題，使得聚類結果更加穩定，且準確實現了對氣象特征的聚類。

2）采用XGBoost 集成機器學習算法，在減少參數設定的同時，相比于GBDT 算法可以得到更加準確的預測結果；對于短期光伏發電功率預測，XGBoost 算法可以更好地適應不同天氣情況帶來的影響。

本文所建立的預測模型在不同天氣情況下均獲得了較好的預測結果，實用性較強，在短期光伏發電功率預測研究方面具有一定的參考價值。