“策略教學”中，數學思維何以進階
——“活課堂”煉制有意義學習

江蘇省南京市江寧區岔路學校 胡 靜

特級教師張齊華老師說過：數學它可以最大限度地張揚數學思考的魅力，并改變一個人的思考方式、方法、視角。數學學習一旦使學生感受到了思維的樂趣，使學生領悟了數學知識的豐富、數學方法的精巧、數學思想的博大、數學思考的美妙，那么，數學的文化價值必然暴露無遺。也只有這樣，我們的數學課才會顯得大氣磅礴、厚重而深遠。

數學教學最根本、最重要的任務是讓學生學會思維。以學生為中心的“活”課堂背景下，在解決問題策略課中，如何促使學生主動思考，讓學生思維有所進階呢？以下結合多年的教學實踐，談談自己的一些粗淺認識。

一﹑激發深層動機，喚醒策略意識，孵化策略雛形

邁向兒童“生活世界”的小學數學教學應該富有童趣、情趣、樂趣，因此我們很多教師喜歡課前設計一些游戲來活躍氣氛，以此引起兒童產生濃厚的學習興趣。

例如，在《解決問題的策略——列表》一課教學中，課前，一位教師設計了這樣一個游戲：

（出示兩組數：1 3 5 2 4 6）

師：同學們，我們來做個比大小的游戲。每次各出一張比大小，為了防止你們說我以大欺小，我把稍微大一點的數2，4，6分給你們好不好啊？也由你們來先出。

師生游戲。

師：老師連勝兩局！明明拿的都是較小的一些數，為什么每次老師都能贏呢？

生：其實，老師您用的就是田忌賽馬故事里的方法，我們出6的時候，你出1，輸一局，當我們出另外兩個數的時候，你用比我們大的數去比，所以你一定會贏。哪個先出，哪個就輸了。

……

此游戲環節的設計，既活躍了氣氛，又喚醒了學生對策略的朦朧意識。針對學生的這種意識和感覺，教師有意識地呈現了兩張不同記錄方式的課程表讓學生暢談“如果是你，你會選擇哪張課程表”，這樣的設計，在不經意間，列表的策略悄然孵化出雛形。

二、“視而不見”與“不依不饒”，催化策略成形

學生的學習歷程應該是他們思維發展的過程，是他們認知框架不斷變革或重組的過程。其中，學習主體的自我反省、自我否定、自我肯定，特別是內在的“經驗沖突”往往構成了認知結構更新的一個重要前提。 在學的過程中，由于學生帶著自己的知識、經驗、思考、創新靈感參與課堂，因此課堂往往出現了許多“節外生枝”“偏離”的現象，如果我們能不拘泥于預設，捕捉一些有價值的“意外”資源，對其合理取舍、恰當地“不依不饒”地引導，必然能讓學生在求知過程中思維有所啟發，更全面、深刻地理解所學的知識。

例如，在教學《解決問題的策略——列表》例題時，讓學生用自己的方式整理題中的條件時，教師精心選取了不同層次的整理“作品”（圖略）。

師：（指1號作品和2號作品）請作者給大家介紹一下你是怎么整理的。

生1：我是畫圖的。

生2：我也是畫圖的，我畫的是線段圖，桃樹3行每行7棵，就畫3個7，杏樹畫8個6，梨樹畫4個5。

師：他們都是用畫圖的方式整理條件的，大家覺得他們的作品怎么樣？

生3:我覺得他們的作品稍微有些麻煩，要一棵一棵畫的話，比較浪費時間。用線段圖也麻煩。如果有很多行，每行有很多棵，那就畫不過來了。

師：那你有什么好辦法？（指3號作品）

生3：我是用文字整理的，分別整理了三種樹的行數和每行的棵樹，把它們對對齊。

師：那3號同學，你覺得你整理的比1號和2號作品好嗎？好在哪？

生3：我的不麻煩，簡潔、簡單。

師：對于3號同學的作品你有什么建議？

生4：添加橫豎線，就更整齊了。

師：（指4號作品）4號作品作者，對比一下3號作品，你有什么不同？這樣列表格有什么好處？

生4：更清晰，一目了然。

師：（呈現5號作品）這個同學也是用列表的方法整理的，他與4號作品有什么不同？

生5：我沒有整理杏樹的信息，因為問題是求桃樹和梨樹一共有多少棵，不需要杏樹的條件。

師：看來整理條件還要關注問題。4號作品，你會進行修改嗎？

生4：去掉杏樹那一行。

師：大家看，修改后的4號作品與5號作品，有什么相同的地方和不同的地方？

生：都是用列表整理條件，整理的都是有關桃樹和梨樹的相關信息，不同的是一個橫著整理，一個豎著整理，看起來都很簡潔。

師：那你是愿意看著圖文整理去分析數量關系，還是看著整理的表格去分析數量關系？

……

對比是人們認識事物和現象的一種常用科學思維方式。通過多次對比，可以清晰地發現知識之間的異同與聯系。在本課中，當兩種繁雜的畫圖方法呈現時，教師并沒有“視而不見”，而是“不依不饒”不斷巧妙地追問，及時引導學生互動，將各種整理方法逐一對比，促進了學生的學習思考，反思和描述自己的思維，比較自己的整理方法與別人的有什么不同，辨別每一種表示方法的優點和不足，針對不足提出建議，不斷優化列表的策略。通過交流、辨析，實現了多元化表征，列表的策略由模糊變得清晰、從淺表轉向深刻。從不會到會，學生的學習真正發生。

三、探尋真實的思維足跡，深度體驗策略

學生都有自己的經驗和思維方式，他們建構知識的過程是一個生動、活潑、自覺、主動、富有個性的過程。學生的思考是學生用自己的經驗繪制的“作品”，蘊藏著學生獨立思考后的“創造”。因此，我們要遵從學生的真實理解和原生態的表達，順應學生的思維歷程，引導學生對問題的認識走向深入，把握知識的本質。讓學生在數學活動中經歷知識的“再創造”過程，促進學生思維的發展，我們的教學才有可能凸顯教學的價值。

【解決問題策略——假設】教學片段。

師：剛才同學們運用多種方法進行一一列舉，現在讀仔細觀察畫出的圖和表，什么在變？什么不變？你發現了什么？小組里說說看。

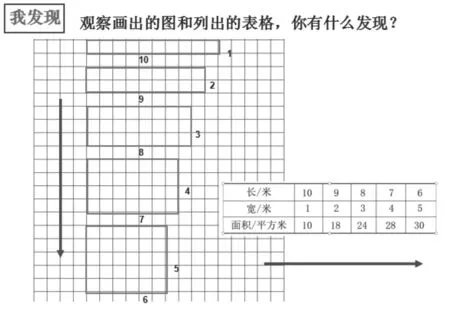
生：周長不變，面積變化。“長+寬”的和是11，也沒有變。

生：長越來越小，寬越來越大，面積越來越大。

生：在周長相等的情況下，長和寬越接近，面積就越大。

師：是不是所有長方形都滿足這樣的規律？老師這里還有一題：王大叔用20根1米長的柵欄圍一個長方形花圃，怎樣圍面積最大？

師：結合剛剛的發現，你們猜一猜，最大的面積會是多少？

生：24，25……

師：究竟是多少呢？用今天的策略來驗證一下。

生：20÷2=10（米），再列舉9×1=9（平方米），8×2=16（平方米）……5×5=25（平方米），因為正方形是特殊的長方形，所以面積最大是25平方米。

師：此時長和寬接近接近再接近，相等的時候，面積最大。

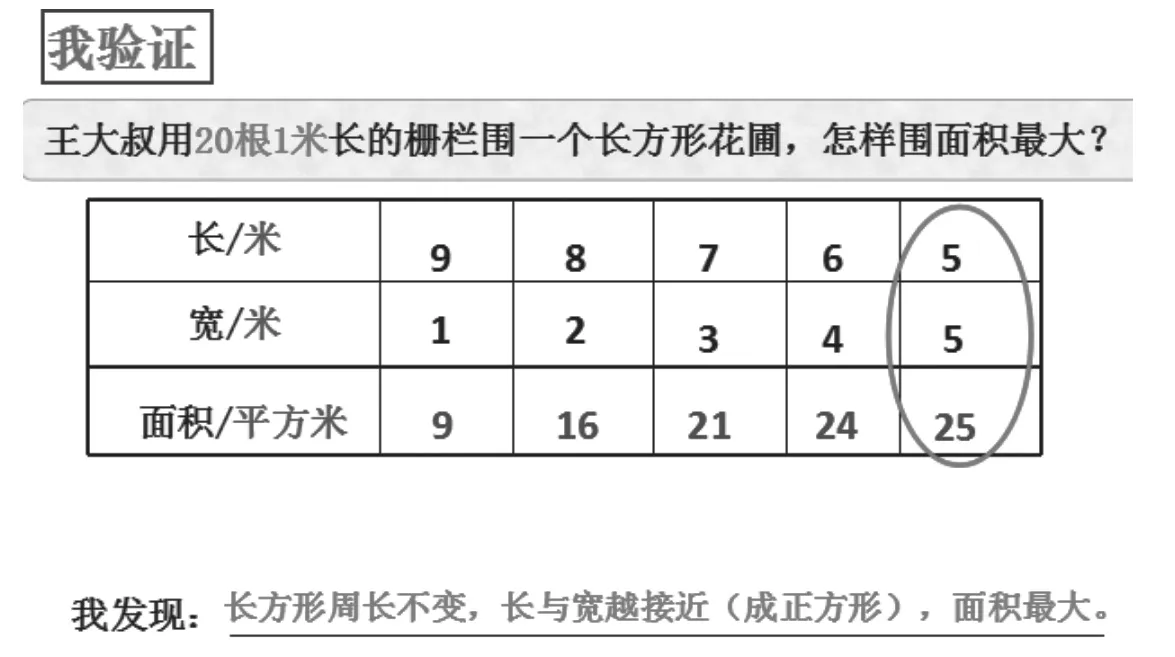
本環節，教師不是為了列舉而列舉，而是通過列舉，引發學生進行有價值的思考，并通過鞏固一一列舉的策略，驗證剛才發現的結論，使之更趨向規律的本質。

【解決問題策略—— 一一列舉】教學片段。

師：其實，在我們以前的學習中就已運用過一些簡單的一一列舉的策略，誰還能想起來？

（生舉例暢談）

師：(引導)一年級，剛學習數的時候，我們就是把10的所有的“分成”都一一列舉出來；三年級，用12個邊長1厘米的正方形拼成不同的長方形，就是用一一列舉的策略把所有的情況都列舉出來；四年級，解決“有序地寫出3張數字卡片能組成所有三位數”這個問題時，也用到了一一列舉的策略。

師：你能用今天的策略有序地說一說嗎？

此環節，教師設計了“再識列舉”環節，開展了連接性學習，教師跨越知識點之間的“鴻溝”，溝通了新舊知識的聯系。跨越年級與年級之間的“界限”，從知識鏈的角度全面審視教材，把握教材的系統性，引導學生深度體驗了一一列舉的策略。通過理性反思，促進策略形成后的鞏固完善和內化提升，在辨識、選擇、運用策略的過程中發展學生的高層次思維能力，構建新的知識體系。

四、把握本質，助力思維“活課堂”

變式練習是將知識轉化為技能的關鍵途徑，有助于激活學生思維的發散性與深刻性。很多教師為了讓學生的思維有質的飛躍，經常在課尾呈現一道稍難一些的變式題或留疑題，引導學生質疑問難，打破思維壁壘，向著知識的本質去探究,實現知識的深度建構，從而讓學生的思維能力得以提升。

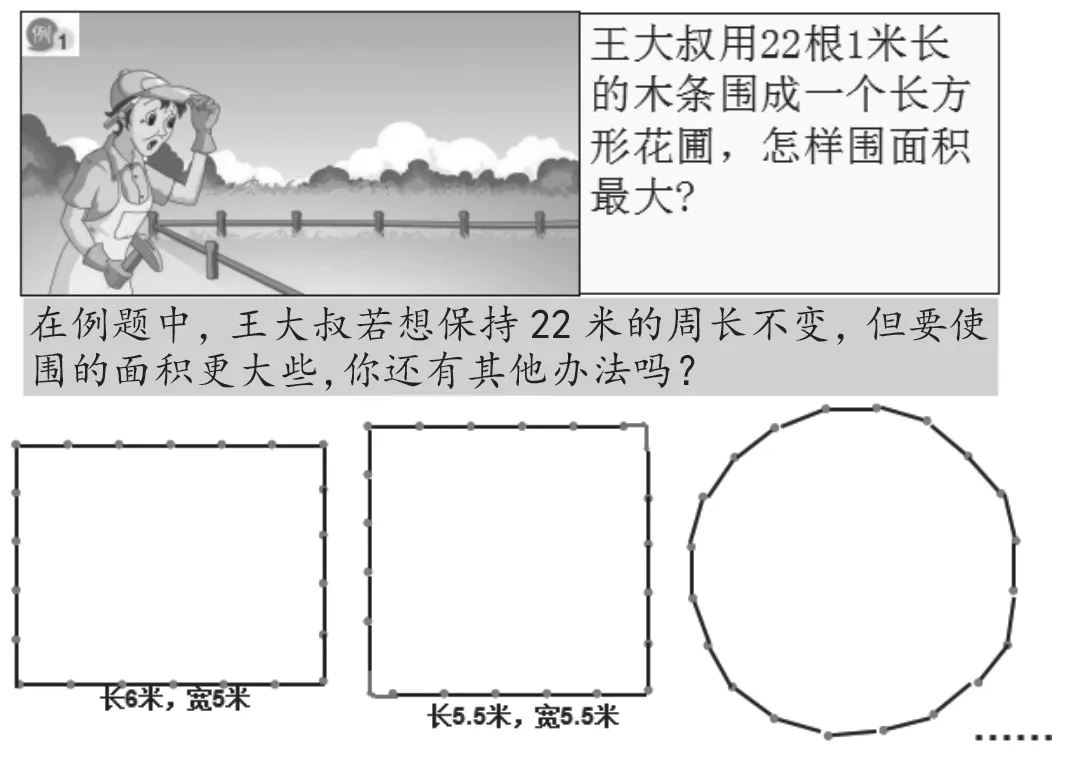
例如，在教學完《解決問題策略——一一列舉》一課時，教師提出問題：回到最初王大叔用木條圍籬笆的問題，如果王大叔只想保持22米的木條總長不變，但要使圍的面積更大些，你還有其他辦法嗎？

再如，在《解決問題策略——假設》一課結束時，教師不斷地追問：如果還有一個迷你杯，這個迷你杯的容量是小杯的，那你知道它相當于大杯容量的幾分之幾嗎？那下面如果還有更小的超級迷你杯，你還能算出來它們的容量大小嗎？為什么這里的迷你杯容量甚至更多未知量你都能算出來呢？

一個小小的“迷你杯”的變式練習，將學生的思維引向深人，讓學生深刻領悟到：把不同量轉化成相同的量，這就是假設的本質。

聚焦核心問題，關注思維發展，讓其有靈性、有智慧、可生長。學生的思維正在一步步地深入，課堂成了活潑潑的思辨之所。這恰是我們努力追尋的“深度學習”的“活課堂”真正樣態。數學的思維活了，“思考”的味道濃了，才能讓富有思考味道的“活課堂”綻放生命的活力，成就學生的精彩。