環(huán)中冪等元的積與差的n-強(qiáng)Drazin逆

魏玉潔，鄒紅林

(湖北師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖北 黃石 435002)

1 引言與預(yù)備引理

設(shè)R是有單位元的結(jié)合環(huán)。N(R)表示R上所有冪零元組成的集合。令comm(a){x∈R|ax=xa}，comm2(a){x∈R|yx=xy,?y∈comm(a)}.

為了讀者的方便，我們先介紹相關(guān)概念。

定義1[8]設(shè)a∈R.若存在x∈R滿(mǎn)足下列條件：

xax=x,ax=xa,a-a2x∈N(R)

則稱(chēng)x是a的Drazin逆，記為x=aD.若x存在，則它一定唯一。RD表示R中所有Drazin可逆的元素組成的集合。

定義2[1]設(shè)n∈,a∈R.若存在x∈R滿(mǎn)足下列條件：

xax=x,ax=xa,an-ax∈N(R)

則稱(chēng)x是a的n-強(qiáng)Drazin逆，記為x=ansD.若x存在，則它一定唯一。RnsD表示R中所有n-強(qiáng)Drazin可逆的元素組成的集合。特別地，當(dāng)n=1時(shí)，稱(chēng)x是a的強(qiáng)Drazin逆。記為x=a1sD=asD.用RsD表示R中所有強(qiáng)Drazin可逆的元素組成的集合。

關(guān)于n-強(qiáng)Drazin逆，文獻(xiàn)[9]中有以下結(jié)論，本文直接以引理的形式給出。

引理1[9]設(shè)n∈，則a∈RnsD當(dāng)且僅當(dāng)a-an+1∈N(R).

引理2[9]設(shè)n∈，若a∈RnsD，則a∈RD且aD=ansD.

根據(jù)引理2和文獻(xiàn)[8]中的定理1可知：設(shè)a∈RnsD.若ab=ba，則ansDb=bansD，即ansD∈comm2(a).

引理3 1) 設(shè)n∈，a,b∈R使得ab=0，則a,b∈RnsD?a+b∈RnsD.

2) 設(shè)n∈，a,b∈R使得ab=ba=0，則a,b∈RnsD?a+b∈RnsD.此時(shí)

(a+b)nsD=ansD+bnsD.

引理4[9]設(shè)a,b∈RnsD，且ab=ba，則ab∈RnsD且(ab)nsD=bnsDansD.

由引理2知，(ab)nsD=(ab)D，再結(jié)合文獻(xiàn)[10]的引理2 ：(ab)D=bDaD=aDbD，所以有，

(ab)nsD=aDbD=ansDbnsD.

引理5[9]若a,b∈R，n∈，則ab∈RnsD?ba∈RnsD，此時(shí)，(ba)nsD=b((ab)nsD)2a.

(ap+b(1-p))nsD=ansDp+bnsD(1-P).

證明 因?yàn)閜2=p，所以p∈RnsD且pnsD=p.已知ap=pa，bp=pb，由引理4得，

ap∈RnsD且(ap)nsD=ansDP，

b(1-p)∈RnsD且(b(1-p))nsD=bnsD(1-p).

因?yàn)閍p·b(1-p)=b(1-p)·ap=0，結(jié)合引理3 2)得，

ap+b(1-p)∈RnsD,(ap+b(1-p))nsD=ansDp+bnsD(1-p)

引理7[9]若a,b∈R，n∈，則1-ab∈RnsD?1-ba∈RnsD.

2 主要結(jié)果

設(shè)p,q是環(huán)R中任意兩個(gè)冪等元，這一節(jié)我們將給出(p-q)2，pq，-(pq-qp)2，(pq+qp)2，pq+qp和pq-qp有n-強(qiáng)Drazin逆的一些條件。

定理1 設(shè)p,q是環(huán)R中任意的兩個(gè)冪等元，則下列命題彼此等價(jià)：

二是要學(xué)習(xí)和實(shí)踐馬克思主義關(guān)于堅(jiān)守人民立場(chǎng)的思想。學(xué)習(xí)這一思想的現(xiàn)實(shí)意義在于增強(qiáng)“共產(chǎn)黨人不忘初心、牢記使命的自覺(jué)擔(dān)當(dāng)”，明確踐履“理論自信”的歸宿。

1) 1-pq∈RnsD2) 1-pqp∈RnsD3)p-pqp∈RnsD4)p-pq∈RnsD，

5)p-qp∈RnsD6) 1-qp∈RnsD7) 1-qpq∈RnsD8)q-qpq∈RnsD，

9)q-qp∈RnsD10)q-pq∈RnsD.

證明 由引理7可知，1)和6)等價(jià).這里只須證1)～5)等價(jià)。

1)?2) 由引理7得，1-pq=1-p(pq)∈RnsD?1-(pq)p=1-pqp∈RnsD.

2)?3) 設(shè)1-pqp∈RnsD，因?yàn)閜2=p，所以p∈RnsD且pnsD=p.又因?yàn)閜(1-pqp)=(1-pqp)p，根據(jù)引理4得，p-pqp∈RnsD.

3)?2) 假設(shè)p-pqp∈RnsD，令a=p-pqp，b=1，顯然有a,b∈RnsD且ap=pa,bp=pb，結(jié)合引理6得：ap+b(1-p)=1-pqp∈RnsD.

3)?4) 因?yàn)閜-pq=p(1-pq)，p-pqp=(1-pq)p，由引理5得，

(1-pq)p∈RnsD?p(1-pq)∈RnsD，即p-pqp∈RnsD?p-pq∈RnsD.

4)?5) 根據(jù)引理5可知，p-pq=p(1-q)∈RnsD?(1-q)p=p-qp∈RnsD.

如果將定理1中的p，q分別用(1-p),(1-q)代替，可以得到下面的結(jié)果：

推論1 設(shè)p,q是環(huán)R中任意的兩個(gè)冪等元，則下列命題彼此等價(jià)：

1)p+q-pq∈RnsD2)p+(1-p)(q-qp)∈RnsD

3) (1-p)q(1-p)∈RnsD4)q-pq∈RnsD

5)q-qp∈RnsD6)p+q-qp∈RnsD

7)q+(1-q)(p-pq)∈RnsD8) (1-q)p(1-q)∈RnsD

9)p-qp∈RnsD10)p-pq∈RnsD

引理8[9]設(shè)n,k∈.若a∈RnsD，則ak∈RnsD且(ak)nsD=(ansD)k.

該引理的逆命題不一定成立，即ak∈RnsD?/a∈RnsD.下面舉例說(shuō)明：

22-(22)n+1=1-1n+1∈N(3).

但是由于

所以a=2不一定是n-強(qiáng)Drazin可逆的。

定理2 設(shè)p∈R，q∈R且p2=p，q2=q，則下列命題彼此等價(jià)：

1) (p-q)2∈RnsD;

2) 1-pq∈RnsD;

3)p+q-pq∈RnsD.

證明 1) ? 2) 假設(shè)(p-q)2∈RnsD.令a=(p-q)2，b=1顯然有a,b∈RnsD，且ap=pa，bp=pb.根據(jù)引理6得，ap+b(1-p)=1-pqp∈RnsD.再結(jié)合定理1中1)和2)可知，1-pq∈RnsD.

2) ? 3) 由定理1中1)和4)知，1-pq∈RnsD?p-pq∈RnsD.因?yàn)?p-pq)q=0，由引理3 1)有，q∈RnsD,p-pq∈RnsD?p+q-pq=(p-pq)+q∈RnsD.

3) ? 1) 假設(shè)a=1-pqp,b=1-(1-p)(1-q)(1-p)，顯然ap=pa，bp=pb.因?yàn)?/p>

1-(1-p)(1-p)(1-q)=p+q-pq∈RnsD

所以由引理7得b∈RnsD。再由定理1 2)和推論1 1)知，a∈RnsD，注意到(p-q)2=ap+b(1-p)，根據(jù)引理6有(p-q)2∈RnsD.

注記1 如果把定理2 1)中的(p-q)2換為p-q，則有 1)? 2) ? 3)，但

p+q-pq∈RnsD?/p-q∈RnsD.

根據(jù)引理8和例1知，p-q∈RnsD?(p-q)2∈RnsD，但是(p-q)2∈RnsD?/p-q∈RnsD.

由定理2知，p+q-pq∈RnsD?(p-q)2∈RnsD，所以p+q-pq∈RnsD?/p-q∈RnsD.下面的例2也說(shuō)明p+q-pq∈RnsD?/p-q∈RnsD.

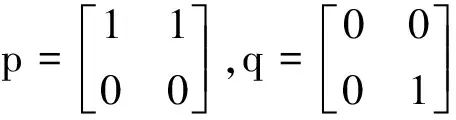
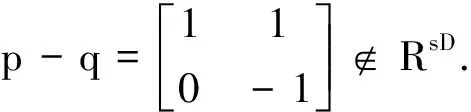
將定理2中的p用1-p代替，則有推論2.

推論2 設(shè)p，q∈R,且p2=p，q2=q，則下列命題彼此等價(jià)：

1) (1-p-q)2∈RnsD;

2) 1-q+pq∈RnsD;

3) 1-p+pq∈RnsD.

定理3 設(shè)p，q∈R,且p2=p，q2=q，則下列命題彼此等價(jià)：

1)pq∈RnsD;

2) (1-p)(1-q)∈RnsD;

3) (1-p-q)2∈RnsD.

證明 假設(shè)p′=1-p，q′=q,則q′-p′q′=pq∈RnsD，p′-p′q′=(1-p)(1-q)，p′-q′=1-p-q.下證命題1)～3)是等價(jià)的：

1) ? 2) 由定理1 4)和10)知，p′-p′q′∈RnsD?q′-p′q′∈RnsD，所以 1)和 2)等價(jià)。

1) ? 3)由定理2 1)和2)和定理1 1)和10)知，

(p′-q′)2∈RnsD?1-p′q′∈RnsD?q′-p′q′∈RnsD

即(1-p-q)2∈RnsD?pq∈RnsD，證畢。

定理4 設(shè)p，q∈R,且p2=p，q2=q，若pq∈RnsD，p+q∈RnsD，則(pq+qp)2∈RnsD.

證明 根據(jù)引理8可知，p+q∈RnsD?(p+q)2∈RnsD.根據(jù)定理3知，

pq∈RnsD?(1-p-q)2∈RnsD

又因?yàn)椋?/p>

pq+qp=(p+q)(p+q-1)=(p+q-1)(p+1)，

再結(jié)合引理4得出，(pq+qp)2=(p+q)2(1-p-q)2=(1-p-q)2(p+q)2∈RnsD.

定理5 設(shè)p，q∈R,且p2=p，q2=q，若pq∈RnsD，p-q∈RnsD，則-(pq-qp)2∈RnsD.

證明 類(lèi)似定理4的證明易知：p-q∈RnsD?(p-q)2∈RnsD，pq∈RnsD?(1-p-q)2∈RnsD.

因?yàn)閜q-qp=-(p-q)(1-p-q)=(1-p-q)(p-q)，從而有

(pq-qp)2=-(p-q)2(1-p-q)2=-(1-p-q)2(p-q)2.

所以結(jié)合引理4可得，

-(pq-qp)2=(p-q)2(1-p-q)2=(1-p-q)2(p-q)2∈RnsD

注記2 定理5不能說(shuō)明(pq-qp)2∈RnsD.容易證得a∈RD?-a∈RD，但是在n-強(qiáng)Drazin逆中a和-a的n-強(qiáng)Drazin可逆性一般沒(méi)有明確的等價(jià)關(guān)系.即，在一般情況下如果a∈RnsD，不一定有-a∈RnsD.

定理6 設(shè)p,q∈R，且p2=p，q2=q，若p+q-1∈RsD，p+q∈RsD，則pq+qp∈RsD且

(pq+qp)nsD=(p+q-1)nsD(p+q)nsD=(p+q)nsD(p+q-1)nsD.

證明 假設(shè)p+q-1∈RnsD，p+q∈RnsD，因?yàn)椋?/p>

(p+q-1)(p+q)=(p+q)(p+q-1)，

根據(jù)引理4，

pq+qp=(p+q)(p+q-1)∈RnsD，

(pq+qp)nsD=(p+q-1)nsD(p+q)nsD=(p+q)nsD(p+q-1)nsD.

引理9[9]設(shè)n∈，a,b∈RnsD使得a2b=aba，則ab∈RnsD.

定理7 設(shè)p，q∈R,且p2=p，q2=q使得pq=pqp，qp=qpq.若p-q∈RnsD，p+q-1∈RnsD，則pq-qp∈RnsD.

證明 假設(shè)p-q∈RnsD，p+q-1∈RnsD.令a=p-q，b=p+q-1，則有a,b∈RnsD，a2b=(p-q)2(p+q-1)=0，aba=(p-q)(p+q-1)(p-q)=0，即a2b=aba.根據(jù)引理9得，ab=(p-q)(p+q-1)=pq-qp∈RnsD.

注記3 定理7反過(guò)來(lái)不一定成立.

p2=p，q2=q，pq=pqp，qp=qpq.

顯然pq-qp=0∈RsD，但是p-q=-1，根據(jù)引理1有，-1-(-1)2=1?N(3)，從而有

p-q?(3)sD.