基于威布爾分布的列車齒輪箱可靠性評估

張棟梁

(南通城市軌道交通有限公司運營分公司 江蘇 南通 226361)

0 引言

隨著列車技術的快速發展及應用需求的不斷提升，用戶對列車系統及其部件提出了更好的可靠性和安全性要求[1]，其中，以齒輪箱為主的傳動系統作為走行部的主要構成，其安全、可靠、平穩運行直接影響并決定了列車運行的安全性、可靠性及經濟性。因此，傳動系統的檢查及維修維護亦是列車日常維保及高級修的重點關注對象[2]。目前，列車傳動系統的可靠性評估主要針對關鍵部件展開，通過數值仿真、故障樹分析及臺架試驗進行研究。但是，數值仿真由于無法復刻實際運營環境，所得結果與實際工況存在一定偏差。故障樹分析是基于原始設計參數展開，更多的是基于經驗數據判斷。最為廣泛采用的臺架試驗，也存在成本高、試驗周期長等缺點。隨著研究的不斷深入，基于統計分析的可靠性預測、基于斷裂力學的可靠性分析以及基于人工智能方法的壽命評估已成為研究機械結構可靠性的主要方法[3]。基于上述理論，對于本文重點研究列車齒輪箱可靠性分析，針對該課題，一些國內學者[4-5]也進行了一系列的研究工作。本文主要采用統計分析方法，對列車齒輪箱的故障數據進行可靠性評估。

1 威布爾分析法

故障分析主要工作是利用大量實際運營故障樣本資料，借助數理統計手段和可靠性理論，揭示列車重點故障發生規律，給出故障的分布函數及其參數的表達式，并且求出可靠性特征量的估計值。目前常用的參數估計分布方法主要有指數分布、威布爾分布和正態分布三種分布方式。其中，威布爾分布能夠將列車運行狀態響應信息與可靠性之間構建映射關系，實現根據運行狀態響應來評估部件運行可靠性，在工程中得到越來越廣泛的應用[6-7]。

兩參數威布爾分布的密度函數為

公式中：m為形狀參數；t為尺寸參數；η為特征壽命。

威布爾分布的可靠度函數為

假設投入n個樣品進行試驗，至t0時刻停止，有r個失效，觀測到失效時間的順序統計量為：t1≤t2≤…≤tr≤t0。其似然函數可寫為

取對數，得到

該方程組為超越方程，需用數值方法迭代求解。

求解步驟如下：

(1)記下式

(2)選初值m0=1

(3)計算

(4)重復上述三步，直至|mk+1-mk|<0.000 1停止迭代。

(5)根據所得mk+1，計算得到

在實際工程應用中，通過以上步驟，結合計算機編程可實現參數求解。

2 齒輪箱故障樣本

根據可靠性抽樣檢驗理論，列車抽樣檢驗的主要有兩種方案：一種是選取多列樣品的抽樣方案，準確性高，試驗時間短；另一種是只取一列樣品的抽樣方案，試驗時間長，精度略低。本文由于采集時間較短，采取第一種方案，在1年多的采集周期內采集4列車的齒輪箱故障數據，每個車組均為16節編組，32個轉向架，10節動車，每個動車有4個齒輪箱，合計40個齒輪箱。列車齒輪箱主要故障模式為“齒輪箱漏油”，“齒輪箱甩油”和“齒輪箱滲油”，由于其失效機理類似，均歸為“齒輪箱漏油”一個大類。截至樣本采集截至時間，共獲得160個樣本數據，145個截尾壽命數據，15個故障數據。

故障頻次圖如圖1所示，頻次分布不符合正態分布和指數分布形式，因此采用威布爾分布方法進行數據處理。

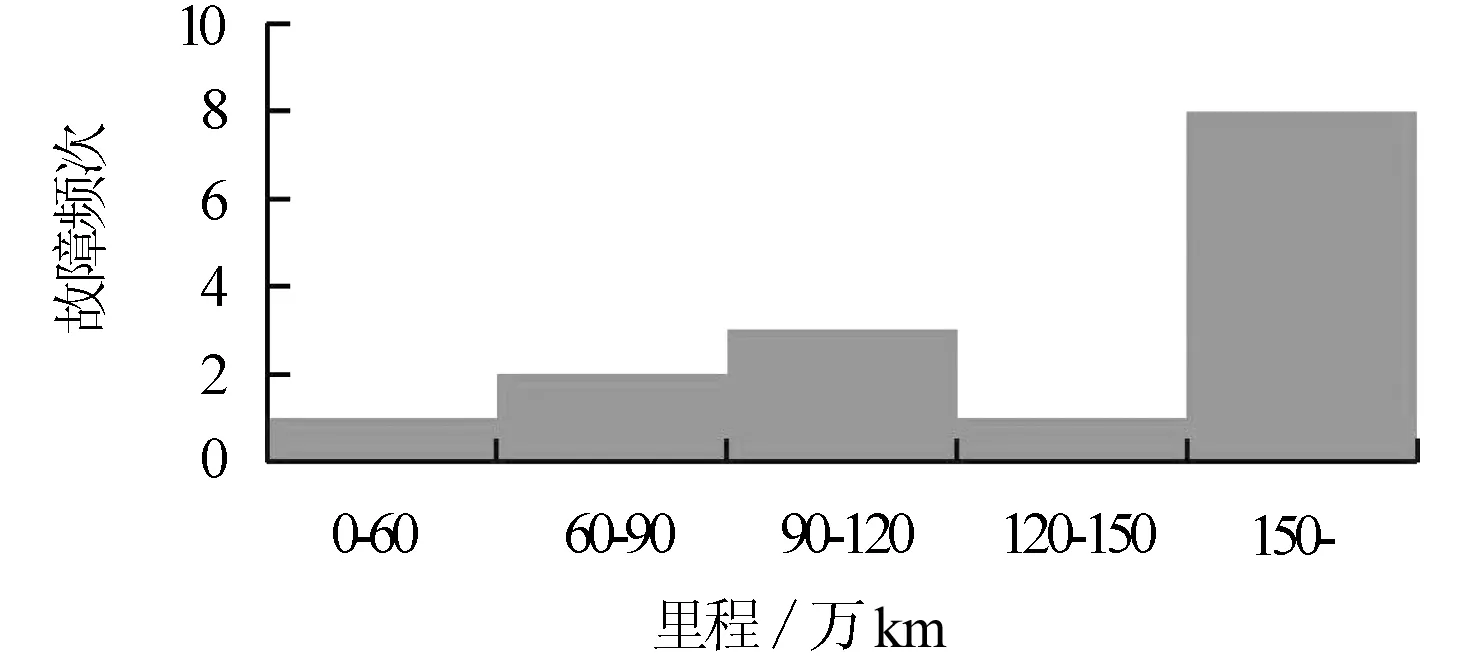
圖1 齒輪箱故障頻次圖

3 齒輪箱可靠性評估

將齒輪箱故障數據帶入第1章節的威布爾分布超越方程進行數值求解，根據第2章節的統計數據可得，n取160，r取15，ti(i=0，1…15)為對應故障的運行公里數，得到m=1.74，η=832。

相應的可靠度函數為

其中：t為里程數(萬km)，繪制可靠性曲線圖，如圖2所示。

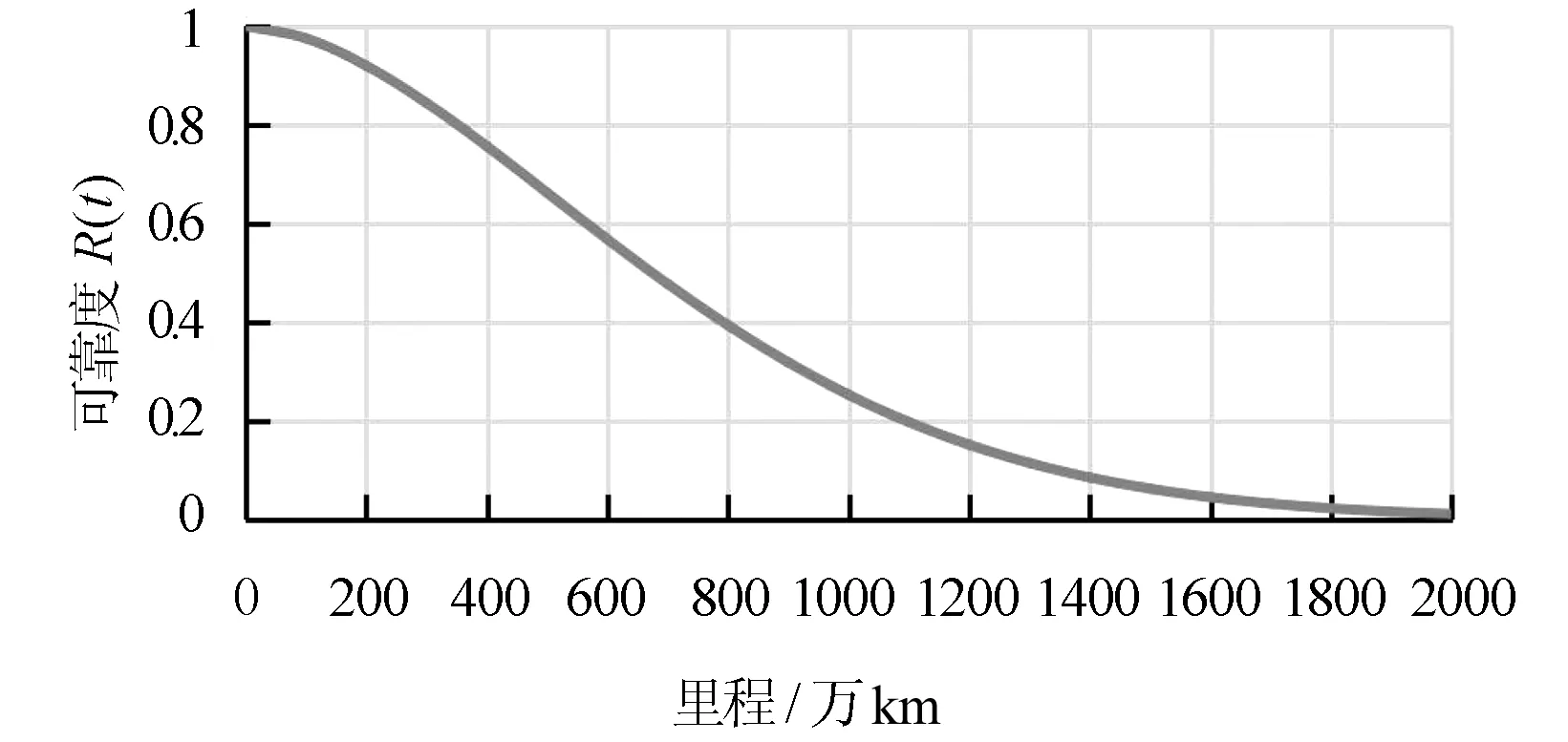
圖2 列車齒輪箱漏油可靠度曲線

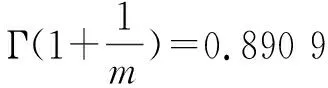
平均失效距離(萬km)為

該車型為16編組車輛，共40個同類型齒輪箱，因此需要進行串聯可靠度計算，即

因此，16節編組列車齒輪箱的平均故障間隔距離(萬km)為

按照該型車出廠的RAMS技術指標，可靠性指標以年運行80萬km進行統計。故以該指標計算得到該型車齒輪箱平均無故障時間(年)為

根據維保現場提供的列車履歷可知列車實際年運行里程為50萬km，因此基于實際運行數據的該型車齒輪箱平均無故障時間(年)為

由計算數值可知，該型車齒輪箱有著較高的可靠性水平，故障率較低。

4 綜合預警評估

隨著車輛運營里程的不斷增加，車輛部件的可靠度不斷下降，日常維保無法滿足可靠性的保障，需要進入高級修程，需要進行一系列專業檢修工作，包含整車檢查及各部件的詳細檢驗及測試，需要較長的扣車周期及檢修成本。但目前進入修程的參考往往以設計制定的里程數為依據。由設計參數可知，該車三級修里程為120萬km，四級修里程為240萬km，根據第3章節求得的可靠度函數可知，該車齒輪箱在三級修時對應可靠度為0.966 2，四級修時對應可靠度為0.891 4，處于較高的水平。

基于以上論述，為了減少扣車時間、節約檢修成本，可以進行以可靠性評估結果為依據的預警研究。目前主要有以下幾種方法：(1)用確定的可靠度值或故障數據率值進行預警，每一個可靠度值或故障率值所對應的里程數進行提醒預警；(2)用可靠度值變化率最大值(可靠度函數二階導數為零)進行預警，即對可靠度函數拐點處的概率值所對應的里程數進行提醒預警； (3)運用三四級修的里程數計算其對應的可靠度值，將當前部件可靠度值與三四級修對應的可靠度值對比，從而對當前部件進行預警； (4)用關鍵部件的MTBF置信上限進行預警。對部件進行區間估計，取區間估計的上限值為部件的最高級預警值，當部件走行里程到達該最高預警值時，進行大修或大面積更換。

綜合多方法多部件的預警結果，結合車輛可用率需求與成本的綜合考慮，可以進行修程修制的優化改進。同時，在高級修后，可根據故障統計結果再次生成可靠性函數，與前次可靠性函數進行對比分析，考量在高級修后部件可靠性的恢復程度，亦可作為高級修的評價指標。

5 總結

本文基于威布爾分布的數理統計方法，給出了可用于工程實際的列車可靠性分析評估方法，并進行了某型車齒輪箱可靠性實例評估。同時，基于該方法總結了列車綜合預警評估方法，以期實現高級修的增效降本的目標。后期，可結合修后故障數據進行對比評估分析，通過多個檢修周期的綜合評估，分析部件尤其是關鍵部件的性能下降情況，為列車整個全壽命周期的分析評估提供參考依據。