關于高速鐵路動車組牽引電機故障預測的研究

荊玉山

(中國國家鐵路集團有限公司 北京 100055)

0 引言

牽引電機是高速鐵路動車組走行部的直接動力來源，目前，對于牽引電機運行狀態的掌握主要依靠安裝于定子鐵芯和兩端軸承的溫度傳感器發送的實時數據，但對其應用則以實時跟蹤為主，更偏向于事后分析，無法在故障發生之前預知或提示。國內對牽引電機的故障預測方法的研究中，趙碩豐[1]等人通過對牽引電機的輸入輸出電流值的監控，建立一種基于諧波分析的牽引電機預測模型。牛齊明[2]等人通過提取牽引電機的振動特性，擬合了牽引電機正常情況下的標準振動數據，通過標準振動數據與運行數據的比對，達到預測牽引電機故障的目的。然而根據本文的調查研究發現，這些預測模型所需要的數據，在高速鐵路動車組中并沒有監控設備可以進行實時傳輸，只能在線下對動車組牽引控制單元進行數據下載得到。在動車組運營單位中，針對動車組某一部件的數據下載，有一定的作業時間及作業周期，因此很難通過這些數據對動車組進行相對實時的信息診斷及故障預測。本文基于動車組WTDS傳輸的實時牽引電機溫度數據，建立了一個牽引電機故障預測模型，滿足一定預測精度的同時，也可以保證應用方面的時效性。

1 動車組牽引電機故障預測模型的建立

目前，多元線性回歸算法[3-7]被廣泛用于各行各業的預測計算。本文結合動車組實際情況，采用多元線性回歸算法建立牽引電機故障預測模型。相較于電流、電壓、振動幅值、振動頻率等數據，牽引電機的溫度數據更容易得到且可以通過溫度傳感器傳輸到WTDS與地面進行實時傳輸。通過動車組運營單位的調查研究發現，牽引電機的異常狀態完全可以通過運行時的溫度特征體現，因此可以將牽引電機運行時的峰值溫度作為研判牽引電機故障的依據。下文以牽引電機溫度峰值作為預測的目標函數，考慮到牽引電機溫度傳感器或者網絡故障引起的牽引電機溫度突變會對函數的擬合結果造成精度缺失，進行預測前需對車載數據進行數據清洗。

對于傳輸的n個運行溫度數據tn，設定篩選變量ε。如果：

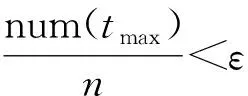
(1)

則對于采集的牽引電機溫度數據tmax進行剔除，對剔除后的n-1個運行數據進行重新清洗，將滿足條件的tmax作為牽引電機溫度峰值。

對于剔除清洗后的n組預測目標數據yn及其k個影響因子xk：

(2)

其中：β1為回歸系數，μ1為隨機擾動項。通過對動車組牽引電機溫度數據的研究發現，動車組在不同運行線路、不同的檢修條件下，牽引電機的溫度峰值有著顯著的不同。分析認為：運行中牽引電機溫度的峰值變化，是一個連續的、相互影響的過程，因此可以由前日牽引電機的運行狀態，結合當日的運行實際對當日牽引電機的溫度峰值進行表征。由于牽引電機采用強迫式風冷散熱，無散熱格柵，結構相對封閉，故外界溫度及天氣狀況因素對牽引電機峰值溫度的影響微乎其微。因此，此處將牽引電機檢修項目信息、運行線路狀況、行車信息及前一天牽引電機運行狀態作為牽引電機溫度峰值預測的影響因子，可以得到較為精準的預測結果。

為保證擬合的回歸方程可以得到良好的精度，根據殘差的平方和最小原則，有：

(3)

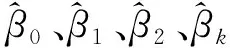
為防止數據中存的離群值xout(對應的殘差具有較大方差的值)降低預測精度，需對離群值xout進行剔除處理。對于n組牽引電機溫度數據yn，使用奈爾檢驗法檢驗離群值，則有：

(5)

(6)

(7)

對數據進行清洗后，則預測值yn+1可以表達為：

(8)

2 牽引電機溫度峰值預測結果

選取一組CRH5A型動車組，對其牽引電機溫度數據進行了長期的數據跟蹤，使用牽引電機故障預測模型，對牽引電機的狀態參數進行預測分析。以7月1日的牽引電機溫度峰值作為預測模型的初始迭代值。將初始迭代步的預測值設置為零，其后的溫度峰值數據作為算法的訓練集。設定篩選度量ε=0.003 5，對溫度傳感器傳輸的溫度數據進行篩選，對清洗后的數據進行預測分析，結果如圖1所示。

觀測圖1中動車組的牽引電機預測結果可知，7月1日至7月20日的牽引電機溫度峰值預測結果均與實際值有較大的差距，這是由于在初始訓練階段，影響因子的系數βk的個數k大于回歸方程的個數n，在回歸分析中，影響因子的系數βk存在空值，因此對于牽引電子的預測結果yn+1呈現著跳動的不穩定性。隨著數據的不斷積累，可用于回歸的方程數目不斷增加，影響因子的系數βk的空值漸漸消除，預測值也逐漸向真實值靠攏。由圖1可知，在經過25天的數據訓練之后，對于CRH5A型動車組牽引電機的峰值溫度預測精度可達92.3%。

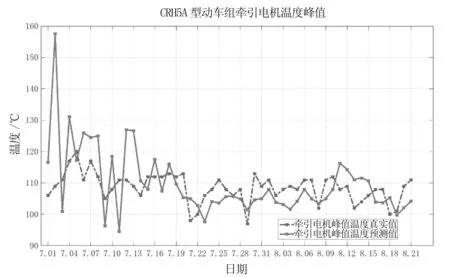
圖1 多元線性回歸算法的CRH5A型動車組牽引電機預測結果

3 預測模型的改進

由圖1可知，采用多元線性回歸算法的預測模型精度可以達到92.3%，但實際生產應用中，8.7%的誤差并不在一個可接受的范圍內。多元線性回歸模型默認各影響因子與預測結果間存在著線性關系，然而生產實際中，簡單的線性關系并不能完全表達兩者間存在的聯系，這就導致了預測值與真實值間存在較大的誤差。本文采用多元非線性回歸算法[8-9]對牽引電機的預測模型進行改進。

在對傳感器傳輸的牽引電機溫度數據進行數據剔除和清洗后，對于采集的組牽引電機溫度數據及牽引電機溫度峰值的各影響因子的數據，構建多元非線性回歸方程：

(9)

對于多元非線性回歸方程，根據殘差的平方和最小原則，有：

(10)

(11)

并使用奈爾檢驗法剔除檢驗離群值xout后，則預測值yn可以表達為：

(12)

4 多元非線性回歸算法的牽引電機溫度峰值預測結果

本文采用多元非線性回歸算法對上述CRH5A型動車組牽引電機溫度數據進行預測分析，以7月1日的牽引電機溫度峰值作為預測模型的初始迭代值。設置初始迭代步的預測值為0,設定篩選變量ε=0.003 5，多元非線性回歸算法與多元線性回歸算法的預測結果如圖2所示。

觀測圖2中動車組的牽引電機預測結果可知，多元非線性回歸算法的收斂周期遠遠大于多元線性回歸算法，經過43天的數據培養后才逐漸收斂于真實值。這是由于多元非線性回歸算法中，雖然未知數的數量與多元線性回歸算法一致，但其影響因子的二次方項同樣需要一定數量的方程進行回歸。在積累到一定數量的數據之后，多元非線性回歸算法也逐漸向真實值靠攏，但其收斂程度遠遠優于多元線性回歸算法，其對于CRH5A型動車組牽引電機的峰值溫度預測精度最終可達95.2%。

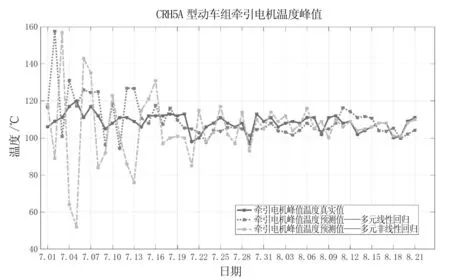
圖2 多元非線性回歸算法的CRH5A型動車組牽引電機預測結果

5 結論

針對目前牽引電機故障預測模型中數據采集困難、實時傳輸不易的問題，提出了一種基于牽引電機溫度的故障預測模型。主要結論如下：

(1)通過多元線性回歸算法建立了牽引電機峰值溫度預測模型，該模型基于溫度傳感器采集的數據，可以滿足實時傳輸的需求。將牽引電機檢修項目信息、運行線路狀況、行車信息及前一天牽引電機運行狀態作為牽引電機溫度峰值預測的影響因子，預測精度可達92.3%。

(2)針對多元線性回歸算法精度難以滿足實際生產需求的問題，使用多元非線性回歸算法對預測模型進行了改進。改進后的預測模型收斂周期增加，但最終可達到的預測精度有了大幅提升。多元非線性回歸算法的牽引電機峰值溫度預測精度可達95.2%。