基于AdaBoost-BAS-SVM模型的巖爆預測研究

劉曉悅 季紅瑜

（華北理工大學電氣工程學院，河北 唐山 063000）

巖爆又稱沖擊地壓，是指發生在深埋地下高應力巖體開挖工程中的一種動力破壞現象，由于硐室應變能的突然釋放引起嚴重的動態危險，整個過程中伴隨著巖體破裂、剝落、分裂、彈射等現象［1-3］。隨著地下工程開挖深度的日益增加，巖爆危險頻繁發生，不僅延誤工期，造成巨大的經濟損失，更威脅著施工人員的生命安全。

由于影響巖爆發生因素眾多，且成因機制復雜，國內外相關學者綜合多種影響巖爆因素，提出多種指標判據，如Russense判據、RQD指標判據、賈愚如判據、秦嶺隧道判據等。隨著機器學習的快速發展，人工智能已應用于巖爆預測預警中。機器學習通過建立各巖爆指標同巖爆強度之間的關系，減少巖爆預警參數選取及數值確定方面的人為干預，從而提高預測精度［4-6］。多種著名機器算法已應用于該領域中［7］，如神經網絡、隨機森林、樸素貝葉斯等。但每種分類器都有其不足之處，如BP神經網絡［8］收斂速度較慢；隨機森林對低維數據分類效果較差，處理回歸問題上易出現過擬合情況；樸素貝葉斯［9］對屬性有關聯的樣本集分類效果不理想。由于巖爆發生是一個不確定且復雜的過程，單一分類器預測結果不夠精準，因此引用集成分類算法，從而提高其預測準確度。

本研究綜合集成算法在巖爆等級預測方面的優勢，將BAS算法優化后的SVM同AdaBoost集成算法相組合對巖爆進行等級預測。SVM作為一種監督式學習方法，算法簡單，且具有較好的魯棒性，廣泛地應用于回歸分析及統計分類方面，但其分類效果受懲罰因子和核函數參數的影響較大。BAS算法作為一種基于天牛覓食原理的仿生優化算法，該方法高效簡單，可快速跳出局部極值，有效地解決了SVM參數尋優問題。AdaBoost作為集成算法Boosting族算法中最著名的代表，具有較低的泛化誤差，不易過擬合。綜合以上分析，建立AdaBoost-BAS-SVM巖爆傾向性等級預測模型，應用于194組巖爆實例數據進行訓練測試，并將該模型與SVM、BAS-SVM、AdaBoost-SVM 3組模型進行對比，證明了AdaBoost-BAS-SVM模型的可靠性及實用性。

1 原理和方法

1.1 AdaBoost算法

AdaBoost［10］算法作為集成算法 Boosting算法中最具有代表性的算法，其核心思想是糾正弱分類器所犯的錯誤。AdaBoost算法屬于一種迭代算法，通過調整迭代次數將弱學習器提升為強學習器。與Bagging算法不同，AdaBoost算法采用串行方式訓練弱分類器，通過增加對前弱分類器分類錯誤樣本的關注度，將訓練后的弱分類器結合為一個強分類器，其基本結構如圖1所示：

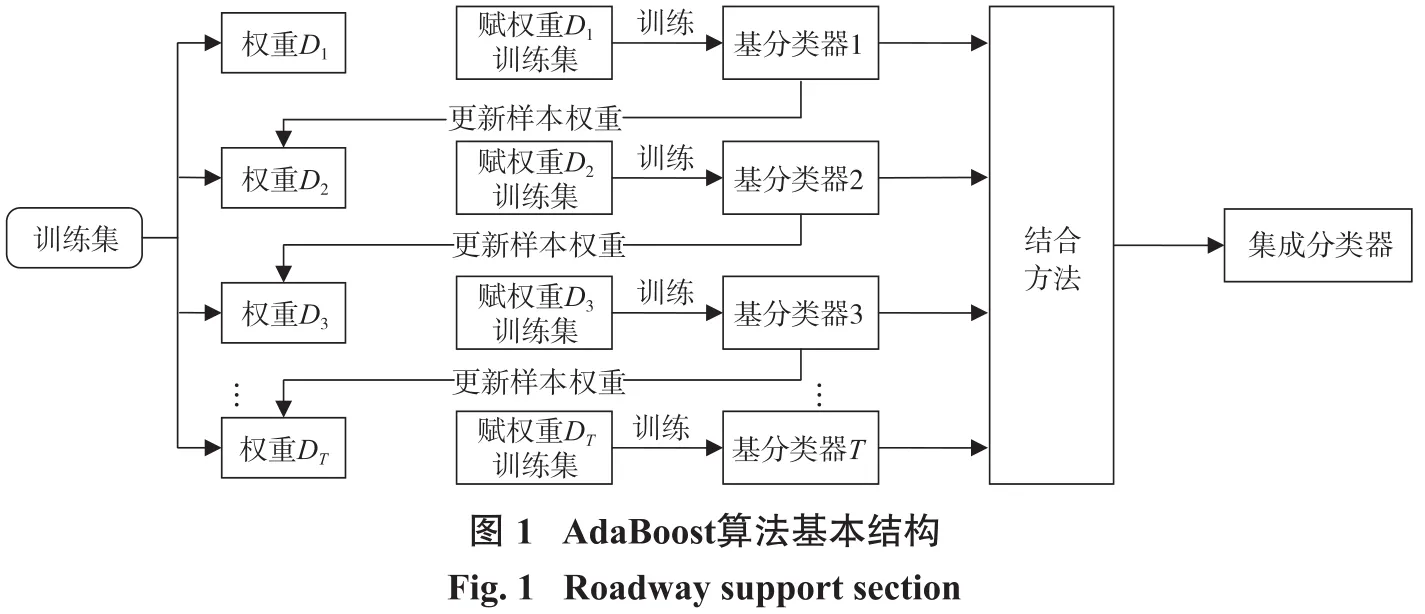
給定基分類器并構建訓練集：G={(x1,y1),(x2,y2),…,(xN,yN)}，其中xi為樣本特征向量，yi為樣本類別標簽，yi∈{- 1,1}，i=1,2,…,N，N表示樣本總數。AdaBoost算法具體實現步驟如下。

（1）初始化訓練集數據的權值向量D1：

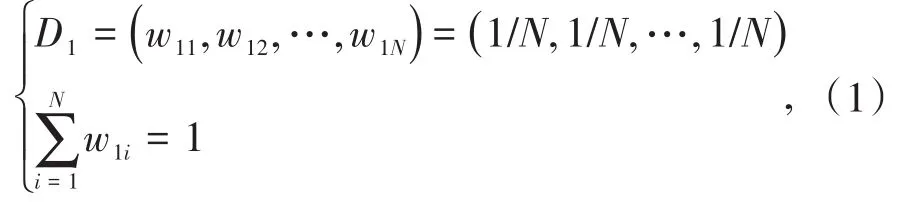
式中，w1i為第i個樣本第1次迭代時的權值。

（2）對基分類器ht進行迭代運算，迭代至第t次時（t=1,2,…,T，T為迭代總次數），計算ht在分布Dt下的預測誤差率et：

計算ht所占權重αt：

更新訓練樣本權值向量Dt+1，并對Zt進行歸一化處理：

對基分類器進行線性加權組合，最終獲得集成分類器H(x)：

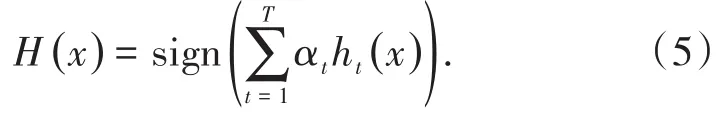
1.2 天牛須搜索算法優化支持向量機（BAS-SVM）算法

1.2.1 支持向量機（SVM）原理

SVM作為一種解決二分類問題的線性分類器［11］，通過在特征空間中尋找具有最大間隔的超平面，從而實現區分不同類別的樣本。SVM算法屬于機器學習中監督學習算法，處理中小型數據樣本、非線性、高維分類問題，有較強的泛化能力。

SVM核心思想是在正確劃分訓練集的同時，使劃分超平面wx+b=0幾何間隔最大。定義樣本空間中樣本點(xi,yi)到超平面的距離，即幾何間隔γi為

式中，w=(w1,w2,…,wd)表示超平面法向量，決定其方向；x為輸入數據；b表示位移項，通常為某實數。

為求得最大間隔劃分超平面，即γi最大，可轉化為有約束最優化問題：

將式（7）中的每條約束添加拉格朗日乘子ai≥0，將有約束問題轉化為無約束問題，構造的拉格朗日函數如下所示：

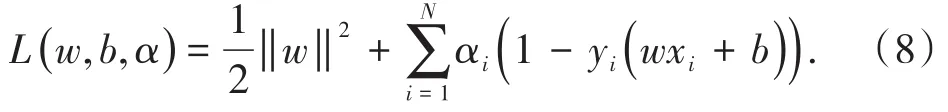
根據對偶原理，將式（8）進一步轉化，得到式（7）的對偶問題：

求出最優解α*、w*，得到最終分類決策函數：

由于輸入空間分為線性分類問題和非線性分類問題，針對非線性分類問題，該方法需將樣本從原始空間映射到高維特征空間，從而樣本在此特征空間內線性可分。在高維特征空間中運用線性支持向量機，該方法的核心是通過核函數K(x,xi)替換xi和xj在特征空間內的內積，因此核函數的選擇不同會生成差異的支持向量機，典型支持向量機網絡如圖2所示。

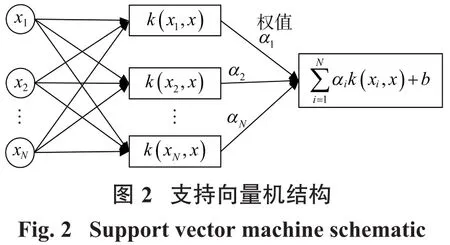
支持向量機算法的關鍵在于核函數及相關參數的選取，常見的核函數有線性核函數、徑向基（RBF）核函數、拉普拉斯核函數等，RBF核函數在處理非線性分類問題上表現優異，因此本文選用RBF函數作為核函數。

1.2.2 基于BAS的SVM參數優化

天牛須搜索（BAS）算法［12］是一種基于昆蟲天牛搜索行為啟發而提出的元啟發式優化算法。該算法模擬了天牛須的作用和自然界中天牛的隨機行走機制，實現了探測和搜索兩個主要步驟。天牛在捕食或尋找配偶時，會擺動身體一側的觸角來接收氣味。即天牛隨機地利用2根觸角探索附近的區域。若天牛一邊的觸角探測到高濃度的氣味時，它就會轉向同一邊，否則它就會轉向另一邊。與群智能相比，BAS具有更高的搜索效率，已應用于許多工程優化問題的求解。BAS建模步驟如下：

Step1：天牛須的方向是任意的，定義一個隨機的方向向量來表示，并進行歸一化處理。

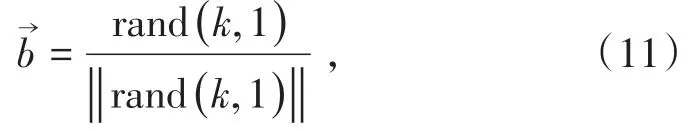
式中，rand(·)為隨機函數；k為位置維數。

Step2：定義天牛左右須的搜索行為坐標。

式中，xr為右側搜索區域內位置；xl為左側搜索區域內位置；d為感知長度，該長度初始設定足夠大，隨著時間的增加而減小，以避免陷入局部極小值；t為迭代次數。

Step3：更新天牛位置。

式中，f(·)為適應度函數；δ為搜索步長，δ、d更新函數如下：

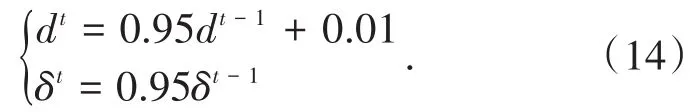
2 巖爆預測模型的建立

將BAS優化后的SVM同AdaBoost算法相結合，建立基于AdaBoost-BAS-SVM算法的巖爆傾向等級預測模型，從而提高巖爆預測精度。

2.1 巖爆等級預測指標選取

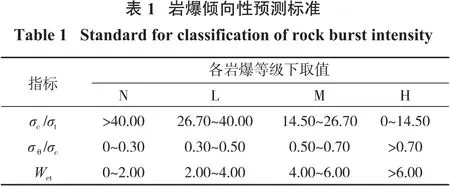
巖爆發生機制復雜，影響因素相對較多，本研究根據巖爆的特點、成因及發生的內外條件，進行綜合分析考慮，選取巖爆傾向性預測評價指標，分別為巖石脆性系數σc/σt、應力系數σθ/σc、彈性能量指數Wet。將巖爆烈度等級分為4類：N（無巖爆活動）、L（輕度巖爆活動）、M（中度巖爆活動）、H（劇烈巖爆活動）。參照王元漢［13］研究成果，各評價指標與巖爆烈度對應關系見表1。

2.2 基于AdaBoost算法的巖爆預測模型訓練

基于AdaBoost集成學習的巖爆預測流程如圖3所示，步驟如下：

Step1：確定BAS參數優化后的SVM為AdaBoost集成學習的弱學習器。

Step2：確定模型超參數：最佳迭代次數（即最佳弱學習器個數）、AdaBoost集成學習的學習率（Learning Rate，LR）。

Step3：根據已獲得的AdaBoost集成學習參數對分類器訓練。

Step4：將已訓練好的AdaBoost分類器經測試集進行檢測，并輸出分類結果。

2.3 模型評價

評價機器學習模型優劣可通過多種評估指標進行衡量，如本文混淆矩陣作為常用的評定監督學習算法性能工具，有助于ML模型分類性能的可視化。巖爆等級分類混淆矩陣如表2所示，其中A、B、C、D分別表示巖爆等級N、L、M、H，矩陣中AA、BB、CC及DD為預測正確的樣本數，其余組合為預測錯誤的樣本數。

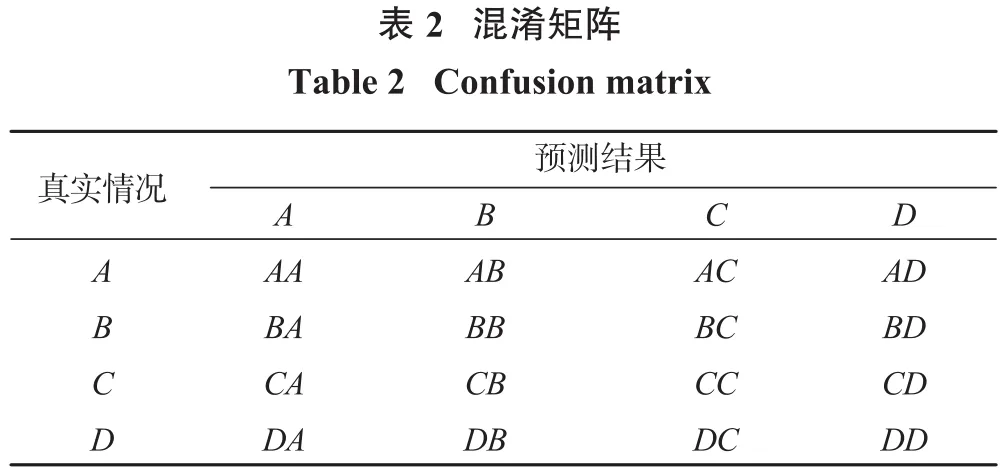
本文選用準確率（Accuracy，ACC）、精確率（Precision，Pr）、召回率（Recall，Re）、F1得分、受試者工作特征（Receiver Operating Characteristic，ROC）曲線以及ROC曲線下面積（Area Under ROC Curve，AUC）6個指標對分類模型性能好壞進行評估，定義如下：

ROC曲線以假正例率（FPR）為橫軸，以真正例率（TPR）為縱軸，對應不同閾值繪制曲線，以體現2指標變化的對應關系。對學習器進行比較時，若學習器A的ROC曲線位于學習器B的上方，則可判定A是優于B的；若兩者的ROC曲線出現交叉時，則可通過比較ROC曲線下面積AUC，AUC值越大，學習器性能越好。

3 實例分析

3.1 實例數據分析及處理

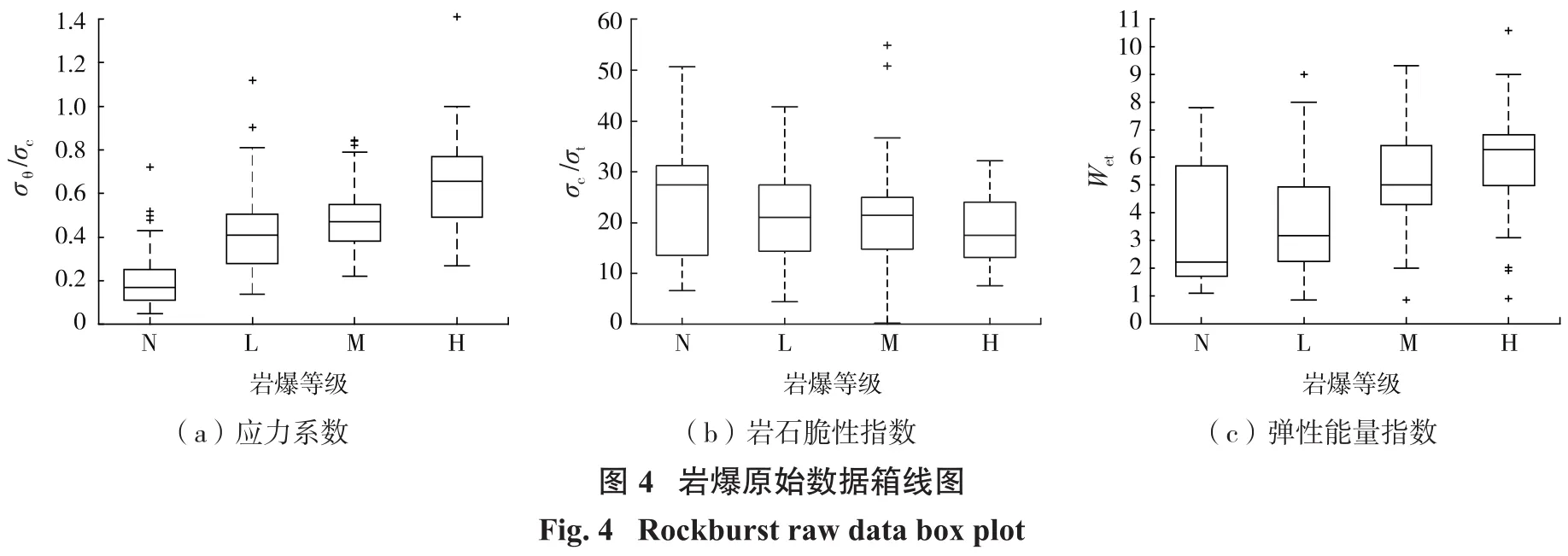
本研究收集了194組國內外已發表文獻中部分礦山巖爆實例的原始數據［14-16］，并將樣本原始數據采用MATLAB程序繪制成箱線圖（如圖4所示）。箱線圖中所示的最小值、最大值、中位數、第一四分位數（Q1）以及第三分位數（Q3），反映出巖爆樣本數據分布不均且存在少數異常值。所收集到的數據集中4類巖爆數據較不均衡，其中無巖爆（N，30組）、輕度巖爆（L，49組）、中度巖爆（M，82組）以及劇烈巖爆（H，33組）。多數分類算法在處理不均衡數據集時都不能獲得較好的分類效果，這是由于分類算法會更多地關注多數類別，從而降低模型對少數類別的分類效果。因此為了解決數據集不平衡引起的問題，本文選用隨機采樣方法處理數據集，其基本原理通過隨機復制少數類別數據從而增加其出現頻率，使各巖爆類別樣本頻數呈均衡。

為提高模型的收斂速度，對原始樣本數據進行歸一化處理，將數據處于區間［0，1］之間，從而使不同維度之間的特征在數值上有一定比較性。由于文章篇幅限制，僅列出部分原始數據及歸一化處理后的數據如表3所示。對處理后的數據按照7∶3的比例劃分訓練集和測試集。為防止模型出現過擬合現象，在劃分之前采用隨機打亂處理，從而提高模型泛化能力。

3.2 模型參數的確定

基于巖爆預測模型SVM提高精確度的目的，本文于1.2.1節中確定徑向基函數為核函數，采用BAS算法對SVM中的懲罰參數C及核函數內的gamma參數進行優化。BAS作為啟發式優化算法，其尋優過程具有隨機性，本文通過多次對比試驗確定算法參數設置：天牛步長衰減系數eta=0.95，天牛須初始步長step=0.8，天牛體型系數c=3，最大迭代次數iter-max=200。經過多次迭代尋得SVM參數最優取值C=5.751，gamma=15.675。

迭代次數及學習率（Learning Rate，LR）作為Ada-Boost集成算法中的重要參數，對分類結果準確率影響很大。一般情況，迭代次數過小，易出現欠擬合現象；迭代次數過大，又易過擬合。同時，在保證同樣訓練集擬合效果的前提下，LR較小則需增加弱學習器的迭代次數。因此，為獲得最佳參數，繪制迭代次數—錯誤率曲線圖，學習率分別取0.2、0.4、0.5、0.9、1.0，如圖5所示。

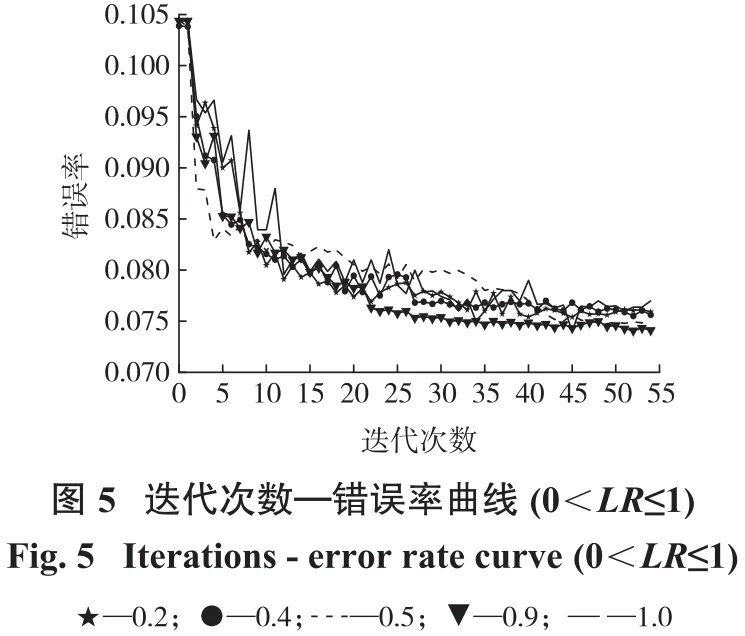
由圖5可知，迭代次數達到46時，5條點線圖走勢趨于平穩，且模型訓練時間同迭代次數大致成正比關系。因此，最佳迭代次數（即最佳弱學習器個數）設置為46。

由圖5中所示的5條LR下曲線可知，分類錯誤率在LR＞0.5時相對較小，所以LR取值應在0.6～1.0之間。進一步改變LR取值，分別繪制LR=0.6，0.7，0.8，0.9，1.0的分類錯誤曲線，如圖6所示。可知，當LR=0.8時錯誤率最低，因此參數LR設置為0.8。

3.3 模型預測結果及對比

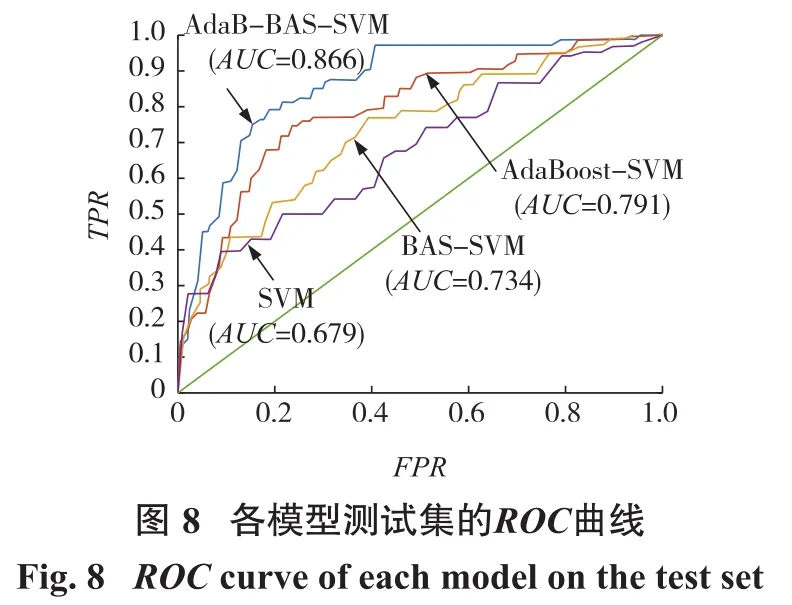
分別將 SVM、BAS-SVM、AdaBoost-SVM 以及AdaBoost-BAS-SVM 4種分類預測模型在測試集進行對比分析，并將預測結果繪制相應的混淆矩陣圖，如圖7所示。

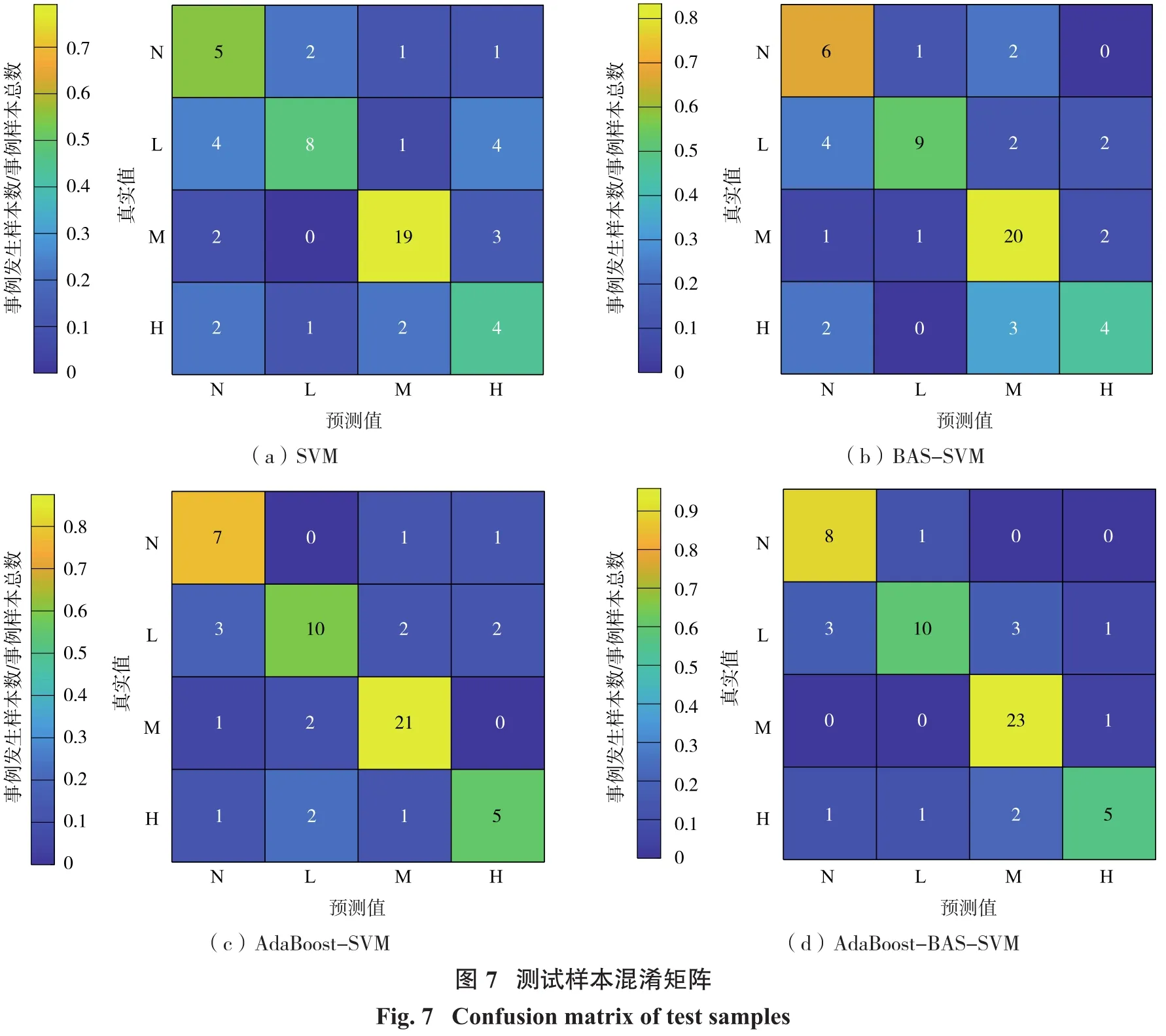
通過所得的混淆矩陣分別計算出各巖爆分類模型的準確率，其中SVM和BAS-SVM單個分類器的準確率分別為61.0%和66.1%，驗證了BAS優化后的SVM分類器較傳統的SVM分類正確率有所增加，分類識別能力有一定提升，但準確率依舊相對較低。AdaBoost-SVM和AdaBoost-BAS-SVM的準確率分別為72.9%和78.0%，均高于單一分類器。由此可見，對于數據不均衡的樣本，單一分類器具有一定局限性，AdaBoost集成學習算法能更準確地劃分巖爆等級。

表4顯示了4個模型在測試集的精確率、召回率以及F1得分。針對得分不均衡數據樣本，上述3個指標更能體現預測模型的優劣。從表中可得，Ada-Boost-BAS-SVM相對于其他模型精確率最高，可達0.759，較單一分類器SVM提高了0.191。結果表明該模型的可行性以及實用性。

分別繪制4種模型下測試集上的ROC曲線，并計算出相應的AUC值，如圖8所示。由圖可得，Ada-Boost-BAS-SVM的ROC曲線，由于閾值取值的改變，TPR隨著FPR遞增而增加，整體走勢呈上凸狀態，且位于其他模型的上方。從AUC值也可看出，Ada-Boost-BAS-SVM的AUC值最高為0.866，與傳統單一分類器SVM相比增加了0.187。由此可見，本文提出的AdaBoost-BAS-SVM巖爆預測模型是合理且有效的。

4 結論

（1）SVM相關參數的優化對巖爆預測結果精確度有較大的影響。本研究采用BAS算法對懲罰參數C及gamma參數進行擇優，在一定程度上提高了SVM模型的預測精度

（2）本研究將AdaBoost集成算法同BAS優化后的SVM算法相結合，融合兩種算法的優點，解決了單一分類器相對不穩定的問題，提高了模型的收斂速度、泛化能力及預測精度。

（3）將本研究建立的AdaBoost-BAS-SVM模型與SVM、BAS-SVM、AdaBoost-SVM 3組模型進行對比分析，所建模型預測準確性顯著提高，證明了本研究所建的巖爆等級預測模型的可行性及有效性。