對汽車車輪動平衡檢測數據的校驗評價

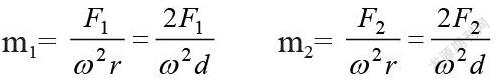
摘 要：隨著我國汽車行業的飛速發展和汽車技術水平的提高，對駕駛汽車時多重路況，以及行駛速度變換要求越來越高，車輪不平衡對汽車安全性能的影響也越來越大，車輪不平衡質量產生的不平衡力的大小和方向在不斷變化，一是整車有上下跳動的趨勢，引起垂直方向的振動，影響汽車行駛平穩性，二是引起轉向輪橫向擺動，影響汽車操縱穩定性和行駛安全。更嚴重的還會造成輪胎、轉向及傳動系統零部件的沖擊和磨損，縮短使用壽命。因此，汽車使用一段時間后，一定要對車輪進行動平衡檢測，測出不平衡質量和相位，并對其校正。國家對車輛的行駛中，要求人員財產安全的保障越來越提到較高的范疇，為確保車輪動平衡機檢測出的數據準確可靠，依據JJF1151—2006《車輪動平衡機校準規范》對各汽修企業以及4S店在用的車輪動平衡機數據校準，校驗。

關鍵詞：車輪;輪動平衡;檢測;校驗

1 汽車車輪動平衡機的工作原理

1.1車輪靜平衡和車輪靜不平衡

車輪靜平衡是一種理想的狀態，要求車輪質心與其幾何、旋轉中心重合。簡單的檢驗方法是：支起車輪，將輪軸調至水平，調整好輪轂軸承的松緊度，用手輕轉車輪，待其自然停轉，此時在車輪離地最底點做一個記號。重復試驗多次，如果每次離地最底點相同，證明車論存在靜不平衡。如果每次試驗自然停轉位置各不相同，則證明車輪是靜平衡。

在實際生活中，不論是新制造的還是使用中的車輪都存在車輪靜不平衡和動不平衡問題，這就需要我們利用車輪動平衡機對車輪不平衡質量及相位的大小進行測試，并對車輪不平衡點的不平衡量予以校正。

對于靜不平衡車輪，其車輪質心與其幾何、旋轉中心不重合，車輪旋轉過程中在不平衡點產生慣性離心力，現將車輪逆時針旋轉360°分析各點慣性離心力的情況，假設車輪的幾何、旋轉中心為O點（即坐標原點），不平衡點的坐標為（r，θ）r是不平衡點的質量距車輪的幾何、旋轉中心的距離，θ不平衡點與x軸的夾角，不平衡點的質量為m，車輪旋轉角速度為ω，車輪轉速為n，ω=2πn，離心力的方向與車輪的切線垂直。根據圓周運動離心力F=4π2mm2，可以看出，離心力F與車輪轉速n、不平衡點的質量m、不平衡點的質量距車輪的幾何、旋轉中心的距離r成正比。離心力F可分解為水平分力Fx=Fcosθ和垂直分力Fy=Fsinθ。在車輪旋轉一周中，垂直分力Fy=Fsinθ有兩次落在通過車輪中心的垂線上，一次在θ=90°，一次在θ=270°，方向相反，均達到最大值，使車輪上下跳動，引起車輪擺振。水平分力Fx=Fcosθ有兩次落在通過車輪中心的水平線上，一次在θ=0°，一次在θ=180°，方向相反，均達到最大值，使車輪前后竄動，造成前輪擺振。當左、右輪的不平衡點的質量相互處于180°位置時，前輪擺振最為嚴重。

1.2車輪動不平衡

靜平衡的車輪在高速旋轉時可能產生不平衡轉矩，出現動不平衡，使車輪產生擺振。在車輪的A、B兩平面內，有兩不平衡點，作用半徑相同（r），相位相反（θ、θ+180°）的兩質點m1、m2， 車輪是靜平衡的。當車輪旋轉時，兩質點產生的離心力形成力偶，使車輪處于動不平衡。如果車輪是轉向輪，那么在力偶的作用下轉向輪就會繞主銷左右擺動。如果在m1、m2同一作用半徑（r）的相反方向（θ+180°、θ）上配上相同質量的m'1=m1、m'2=m2，形成一個與m1、m2，相反方向的平衡轉矩，此時的車輪處于動平衡狀態，經過以上分析可知：靜平衡的車輪不一定是動平衡的，但動平衡的車輪一定是靜平衡的，因此，國家對車輪必須進行動平衡檢測，以確保車輛行駛安全。

1.3車輪動不平衡檢測方法

（1）靜不平衡

安裝在特制平衡軸或平衡機轉軸上的車輪，如果不平衡，在自由轉動狀態下，其不平衡點處于最下面的位置才能保持靜止狀態，給車輪不平衡點配重平衡后，車輪停于任一位置。利用物體平衡原理，可測得車輪的靜不平衡點的質量和相位。

車輪平衡機檢測車輪靜不平衡的原理就是支承離地面的車輪如果不平衡，車輪轉動時產生的上下振動通過轉向節或懸架傳遞給檢測裝置的傳感磁頭、可調支架和底座內的傳感器。傳感器變成的電信號控制頻間燈閃光，以指示車輪不平衡點位置，并由輸入指示裝置指示不平衡質量和相位。

（2）動不平衡

現在以硬支撐平衡機為例來分析離車式車輪動平衡機的工作原理，硬支撐是指支撐剛度很大，車輪支撐系統振動很小，車輪的慣性力可以略去不計。

平衡機主軸長為L， 并且L>a+b+c， 其中：a是被測車輪距N2支撐點的距離;b是被測車輪輪輞寬度;c是平衡機主軸N1、N2兩支撐點之間的距離，c為平衡機的結構參數，N1、N2為兩支撐點的動反力，由相應傳感器轉換成電信號后測出。

設有不平衡質量m1、m2，集中在兩側輪輞的邊緣處，且在同一方向，車輪旋轉時質量m1、m2產生的離心力為F1，F2 ，N1、N2為平衡機主軸左右支撐測得的動反力，由相應傳感器轉換成電信號后測出，根據物體平衡條件，力和力矩的平衡條件有：

已知：a、b、c、N1、N2就可計算出F1，F2，再根據離心力計算公式F=mrω2，求出不平衡質量m1、m2，式中：ω為車輪平衡時動平衡機主軸的轉動角速度，r為不平衡點質量到車輪旋轉中心的距離，一般平衡塊安裝在輪輞邊緣，所以r=d/2，d是被測車輪輪輞直徑，可查看輪胎代號讀取。

2 動平衡機標準器校驗轉子和試重砝碼應改進

2.1標準校驗轉子

在實際使用動平衡機對車輪作動平衡試驗時，動平衡機檢測出來不平衡點的相位是（0～360）°任意一點，為提高動平衡機相位的校準能力，應將校驗轉子的A、B校正平面軸向的12個螺孔（相位差30°）設計成360°任意一點。

2.2試重砝碼

首先應熟悉每個試重砝碼（5g、10g、20g、30g、40g、50g、60g、80g、100g、120g）幾何形狀是由大圓柱和小圓柱質量構成，其中小圓柱帶絲扣為擰在校驗轉子上。設試重砝碼的質心與它的幾何中心重合，當試重砝碼不論加在A或B校正平面上，還是加在A或B非校正平面上，都會影響校準結果。

現在來分析：以試重砝碼加在A校正平面上為例，進行受力分析，A校正平面的質心與幾何中心重合為O點，當動平衡機以角速度ω旋轉時，試重砝碼產生離心力，其方向由O點指向試重砝碼的質心并與A校正平面的夾角為α，離心力為F與主軸不垂直，離心力可分解成兩個分力，一個垂直于主軸分力Fcosα;一個沿主軸方向分力Fsinα，該分力會影響動平衡機的校準結果，只要α=0°時，Fsinα=0，沿主軸方向分力為零，才不會影響動平衡機的校準結果。

如將每個試重砝碼的幾何形狀設計成兩個大小一樣的圓柱形并自帶螺口，兩個圓柱形組合在一塊就成為一個圓柱形砝碼，將該試重砝碼加在A校正平面上時，試重砝碼的質心與A校正平面的質心在同一平面上，即α=0°，沿主軸方向分力為零，這樣設計試重砝碼形狀結構就不會影響動平衡機的校準結果。

參考文獻：

[1] 楊靜芳. 輪胎動平衡在線檢測試驗機研制及其關鍵技術研究[D]. 山東：山東大學，2015.

[2] 王洪，彭熙偉，李占宏，等. 基于FFT的車輪動平衡檢測技術[J]. 北京理工大學學報，2002，22（3）：300-302.

作者簡介：

張建剛（1964.01—），男，漢，籍貫：內蒙古自治區省呼和浩特市人，大學本科，現職稱：工程師，研究方向：企業評價及汽車召回。