基于改進狼群算法的概率積分法模型參數反演方法

李靖宇，王 磊，江克貴，滕超群

( 安徽理工大學 測繪學院，安徽 淮南 232001 )

我國能源資源結構具有“富煤、貧油、少氣”的特點，其中煤炭資源在一次能源結構的生產和消費中所占比例高達76%和66%，因此在可再生資源形成規模之前，煤炭將長期作為主體能源擔負著國家能源安全和經濟持續發展的重任[1]。高強度的煤炭開采勢必會造成礦區環境災害問題，如地面塌陷、工程地質損害等，開采沉陷預計對于“三下”采煤、礦區環境災害防治可起到指導性作用，因而開采沉陷預計一直是我國礦山領域的熱點問題。概率積分法是我國普遍采用的開采沉陷預計方法，該方法已積累大量的實踐經驗，形成了相對成熟的預計參數體系[2]，如何基于實測數據，精確、快速、可靠地獲得概率積分法模型參數，一直是該方法應用的難點。

概率積分法模型參數反演主要經歷了特征點法、線性近似法[3]、正交實驗法[4]，特征點法因曲線特征點難以精確確定進而導致求參誤差大；線性近似法對模型參數初值要求極高，若初值精度不高，則會導致求參模型發散；正交實驗法求參速度慢且不易借助計算機實施；針對概率積分法模型參數反演中存在的問題，一些專家學者提出采用智能優化算法反演概率積分法模型參數。查劍鋒[5]等利用遺傳算法進行概率積分法模型參數反演，此后又有專家學者將粒子群算法[6]、人工蜂群算法[7]、果蠅算法[8]引入到了概率積分法模型參數反演中，為概率積分模型參數反演提供了新途徑。近年來，吳虎勝[9]等提出了狼群算法，與傳統智能優化算法相比，狼群算法具有收斂速度較快、可有效避免局部最優解、統計結果精度較高等良好的尋優特性；文獻[10-12]對狼群算法提出了改進方案，進一步提高了狼群算法的尋優特性。目前，狼群算法已在移動機器人路徑規劃[13]、橋起主梁優化[14]、井下排水采氣超聲速噴嘴優化[15]等領域得到了廣泛應用，但鮮有概率積分法模型參數反演方面的案例報道。

鑒于此，本文在分析狼群算法優缺點的基礎上提出二次游走、變異行為改進策略，形成了改進狼群算法( IWPA )，與狼群算法相比，改進狼群算法的搜索精細程度、跳出局部最優解能力得到了有效提高，并將改進狼群算法引入概率積分法模型參數反演中，構建改進狼群算法的概率積分法模型參數反演方法( MIWPA )。

1 反演方法

1.1 基本狼群算法

人工狼群狩獵區域[15]為一個N×D的歐氏空間( N為人工狼總數，D為待求參數維度 )，任意一匹人工狼為Wn＝( wn1，wn2，…，wnd，…，wnD)。在人工狼群中，每一匹人工狼都是隨機生成的，隨機生成人工狼的公式為

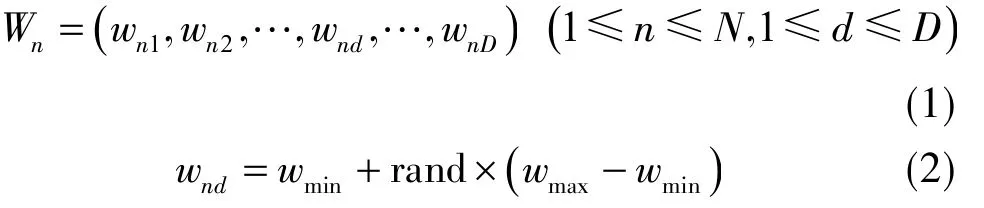
式中，wnd為第n匹人工狼在第d維空間中的位置( 即第n組隨機參數中的第d個參數 )；wmax，wmin分別為wnd中的最大值、最小值；rand為-1至1之間均勻分布的隨機數。

( 1 ) 頭狼產生規則

在人工狼群中，頭狼感知氣味濃度最大，頭狼不斷變化且不參與游行、奔襲、圍攻行為。

( 2 ) 游走行為

探狼是除頭狼外、感知氣味濃度較大的人工狼。探狼每次游走向不同方向前進，每次前進后返回原來位置，若探狼前進后感知氣味濃度超過頭狼感知氣味濃度，則更新頭狼并進行奔襲行為，若不是，則繼續游走直至更新頭狼或達到最大游走次數；游走結束后，若探狼感知最大氣味濃度大于當前位置感知氣味濃度，則更新探狼。第k次前進后，探狼的位置為

式中，wnd為開始搜尋獵物前，探狼在第d維空間中的位置；step ad為探狼在第d維空間中的游走步長。

( 3 ) 奔襲行為

猛狼是距頭狼較近的人工狼。猛狼在奔襲過程中，若感知氣味濃度超過頭狼感知氣味濃度，則更新頭狼且繼續奔襲行為，直至猛狼與頭狼之間的距離滿足要求。猛狼奔襲后的位置為

式中，wnd為猛狼在第d維空間中的位置；step bd為猛狼在第d維空間中的奔襲步長為頭狼在第d維空間中的位置。

( 4 ) 圍攻行為

猛狼、探狼接收頭狼的信號后，開始圍攻獵物，若每次攻擊后感知氣味濃度超過原位置感知氣味濃度，則更新該人工狼。第k+1次攻擊后的位置為

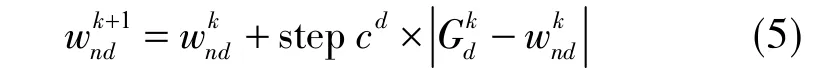
( 5 ) 狼群更新規則

圍攻結束后，淘汰感知氣味濃度較小的人工狼，同時根據式( 1 )，( 2 )隨機生成相同數量的人工狼。

1.2 狼群算法改進策略

( 1 ) 二次游走

在狼群算法游走行為中，存在下述問題：首先，對于某一探狼而言，其游走方向數固定不變；其次，當探狼游走至獵物附近時，游走步長可能會超出探狼與頭狼間的距離，游走后無法感知更大的氣味濃度，此時探狼與獵物間雖具有一定距離，但無法進一步靠近獵物；最后，當探狼與獵物間的初始距離較大時，游走后感知更大的氣味濃度并向獵物前進，但游走步長可能略小，直至游走結束，距離獵物仍有一定距離。假如探狼A，B游走方向數為4，則狼群算法游走方式如圖1所示。

針對上述問題，為提高狼群算法的搜索精細程度，提出了二次游走改進策略，其思想如下：

① 將狼群算法探狼游走視為一次游走，探狼選擇以一次游走感知氣味濃度最大的方位為起點，進行二次游走。

圖1 WPA探狼游走Fig.1 WPA spies the wolf

② 探狼二次游走時，根據一次游走結果，做出不同的反應：對于探狼A而言，其二次游走與一次游走相比，方向數相同但步長較長；對于探狼B而言，其二次游走與一次游走相比，方向數較多且步長較短。

假如探狼A，B游走方向數為4，則改進狼群算法游走方式如圖2所示。

圖2 IWPA探狼游走Fig.2 IWPA spies away

③ 探狼二次游走中，每一次前進后，返回二次游走前位置，第m次前進后的位置為

式中，wnd1為探狼一次游走感知氣味濃度較大的方位為探狼第d維空間中的二次游走步長。

( 2 ) 變異行為

狼群算法為跳出局部最優解，對狼群進行狼群更新：淘汰部分感知氣味濃度較低的人工狼并隨機生成等數量的人工狼；但生成的大部分人工狼適應度函數較低或距離頭狼較遠，無法成為探狼或猛狼，因此沒有參與到狼群游走、奔襲、圍攻行為中，并在下一次迭代前的狼群更新中被淘汰，從而導致狼群算法跳出局部最優解能力受到限制。針對上述問題，提出變異行為改進策略，其思想如下。

① 召喚行為后，狼群并不立刻進行圍攻行為，而是將頭狼與其他人工狼按比例混合，如式( 7 )所示。

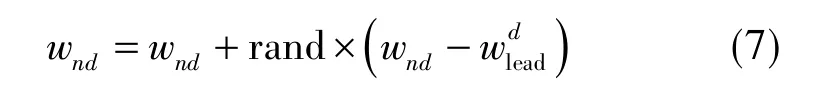
② 混合后，若人工狼感知的氣味濃度變大，則更新其位置。

③ 人工狼更新后，重新選擇頭狼、探狼、猛狼并進行圍攻行為。

1.3 反演方法構建

根據1.2節改進的狼群算法，結合開采沉陷概率積分預計模型，提出了基于改進狼群算法的概率積分法模型參數反演方法，其主要過程如下：

Step 1：地面實測下沉值、水平移動值分別記為Ss，Ms，利用概率積分法模型參數計算的預計下沉值、水平移動值分別記為Sy，My，以實測值與預計值之差平方和最小為準則，構建適應度函數為

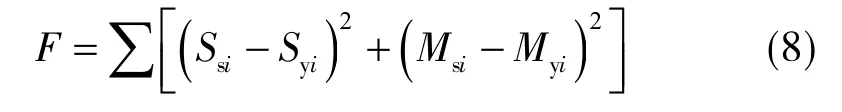
式中，Ssi，Msi，Syi，Myi分別為地面觀測點( Xi，Yi)對應的Ss，Ms，Sy，My。

Step 2：設置狼群數量N、最大迭代次數Dmax、最大游走次數Tmax等參數；給定概率積分法模型參數中心值B0＝[q0，tan β0，b0，θ0，S10，S20，S30，S40]，各概率積分法模型參數的波動范圍ΔB＝[Δq，Δtan β，Δb，Δθ，ΔS1，ΔS2，ΔS3，ΔS4]，生成人工狼群Bi＝[qi，tan βi，bi，θi，S1i，S2i，S3i，S4i]( i＝1，…，N )。

Step 3：以適應度函數值為判斷人工狼感知氣味濃度Yn大小的依據，適應度函數值越小則人工狼感知氣味濃度越大，選擇感知氣味濃度最大的人工狼為頭狼，記其位置、感知氣味濃度分別為wlead，Ylead。

Step 4：選擇除頭狼外、感知氣味濃度較大的人工狼為探狼，探狼根據式( 3 )進行一次游走后，根據式( 6 )進行二次游走，直至二次游走后探狼感知氣味濃度Yn2＞Ylead或游走次數T＝Tmax后，進行奔襲行為，若Yn2大于一次游走后該探狼感知氣味濃度Yn，則更新該探狼。

Step 5：選擇距離頭狼較近的人工狼為猛狼，猛狼根據式( 4 )向頭狼奔襲，若奔襲過程中猛狼感知氣味濃度Yn＞Ylead，則更新頭狼，繼續召喚行為；若Yn＜Ylead，則猛狼繼續奔襲，直至猛狼與頭狼間距離Dn小于要求距離D。

Step 6：根據式( 7 )，對人工狼進行變異，若變異后感知氣味濃度YnB大于變異前感知氣味濃度Yn，則更新該人工狼，變異結束后重新選擇頭狼、探狼、猛狼。

Step 7：根據式( 5 )，探狼聯合猛狼對獵物進行圍攻。

Step 8：對頭狼進行更新，淘汰部分感知氣味濃度較小的人工狼，并根據式( 1 )，( 2 )隨機生成等數量人工狼。

Step 9：判斷是否達到精度要求或最大迭代次數Dmax，若達到，則輸出頭狼位置，即概率積分法模型參數，否則轉至Step 3。

基于改進狼群算法的概率積分法模型參數反演方法( MIWPA )的運行流程如圖3所示。

圖3 MIWPA流程Fig.3 Flow chart of MIWPA

2 模擬試驗

2.1 工作面概況

以淮南礦區地質采礦條件為背景，模擬工作面走向開采長度D3＝800 m，傾向開采長度D1＝300 m，煤層平均采厚m＝3 m，煤層傾角α＝5°，平均采深400 m，采用全部垮落法管理頂板開采。在工作面走向每隔20 m布設1個監測點，共51個監測點；沿工作面傾向每隔20 m布設1個監測點，共36個監測點，模擬工作面如圖4所示。礦區概率積分法模型參數為：下沉系數q＝0.8，水平移動系數b＝0.25，主要影響角正切tan β＝2.5，最大下沉角θ＝85°，上、下、左、右拐點偏移距為S1＝S2＝S3＝S4＝60 m。

圖4 模擬工作面及地表監測點布置Fig.4 Schematic diagram of simulated working face and surface monitoring points

2.2 改進狼群算法參數估計準確性

分別利用MWPA，MIWPA進行概率積分法模型參數反演，試驗設計方案如下：參數q，tan β，b，θ，S1，S2，S3，S4波動范圍分別為0.5～1.1，2.0～3.0，0.05～0.45，82～88，40～80，40～80，40～80，40～80，為了防止試驗結果出現偶然性，進行10次概率積分法模型參數反演試驗，計算參數中誤差及參數相對誤差，試驗結果見表1。

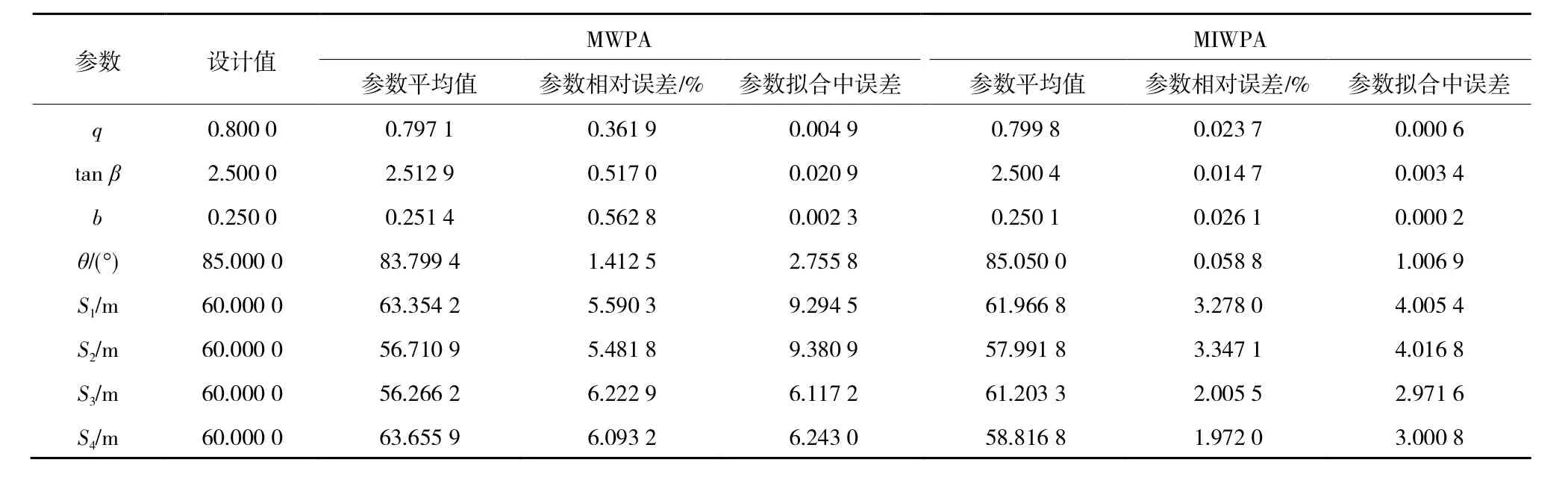
表1 MWPA 和MIWPA 參數估計值與設計值對比Table 1 Estimated values of MWPA and MIWPA parameters were compared with the design values

由表1可知：在參數相對誤差方面，MWPA反演參數相對誤差最大不超過6.3%，MIWPA反演參數相對誤差最大控制在3.4%以內。在參數擬合中誤差方面，MIWPA反演參數擬合中誤差均小于MWPA，MWPA反演參數中誤差最大不超過9.39，MIWPA反演參數中誤差最大不超過4.02。

試驗結果表明，與MWPA的反演參數結果相比，MIWPA方法更加穩健，且參數反演參數精度大幅提高。

2.3 改進狼群算法的可靠性

為進一步證明MIWPA的可靠性，基于模擬試驗，分別利用MWPA和MIWPA反演概率積分模型參數10次，反演參數結果的波動情況如圖5所示。由圖5可知，與MWPA相比較，MIWPA反演參數波動范圍較小，反演參數更接近于真實值。

綜上所述，MIWPA反演參數的穩定性、精度均優于MWPA，MIWPA反演概率積分法模型參數具有更好的可靠性。

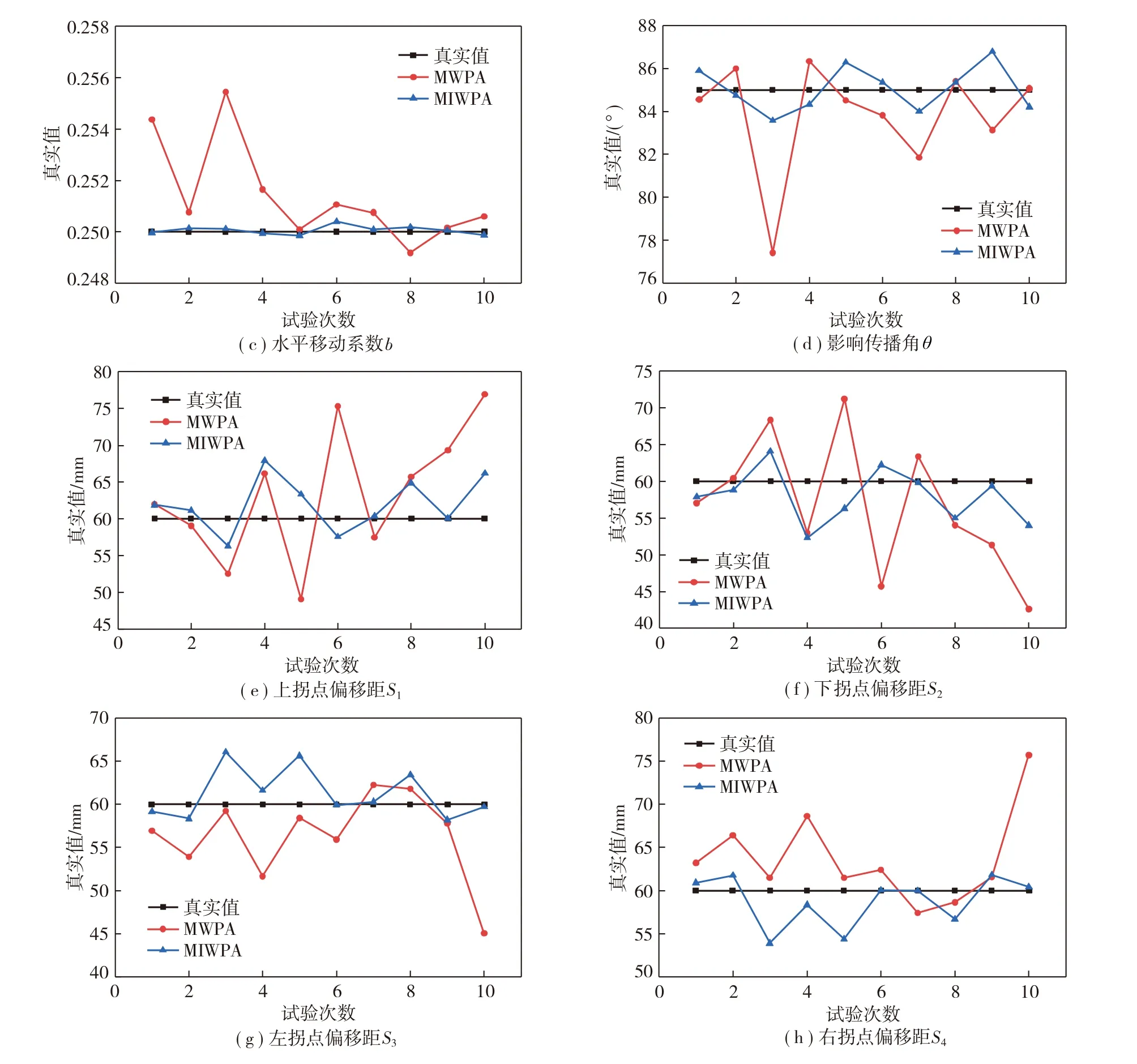
圖5 10次模擬試驗反演參數波動情況Fig.5 Fluctuation of parameters was inversed in 10 simulation experiments

3 工程實例

3.1 礦區概況

淮南顧橋南礦1414( 1 )為顧橋煤礦南區的第1個回采工作面，工作面從礦床邊界開始向巷道往回開采，采用機械化掘進，垮落法管理頂板，一次采全高，工作面地質采礦條件為：走向開采長度2 120 m，傾向開采長度251 m，平均采深735 m，煤層平均采厚3 m，煤層傾角5°。主斷面傾向觀測線布置在距開切眼約1 144 m、終采線約976 m處，傾向線長度為1 500 m，相鄰點之間點間距為30 m，共布設3個控制點和50個監測點。主斷面走向觀測線布置在下山方向偏離工作面中心線39 m的方向上，走向線長度約3 480 m，相鄰點之間點間距為30 m/60 m，共布設3個控制點和95個監測點。觀測站布設如圖6所示。

圖6 觀測站布設Fig.6 Observation station layout

3.2 試驗結果及分析

將顧橋南礦1414( 1 )的實測數據經過預處理，在走向線上選取75個監測點，在傾向線上選取47個監測點，利用MWPA，MIWPA進行概率積分法模型參數反演。為避免試驗的偶然性，進行了10次試驗，然后分別計算參數平均值與參數中誤差。其結果見表2。

表2 MWPA 和MIWPA 在工程應用中求參結果比較Table 2 Comparison of parameter calculation results between MWPA and MIWPA in engineering application

由表2可知：從參數中誤差方面來看，MIWPA反演參數q，tan β，b，θ中誤差控制在0.88以內，拐點偏移距S1，S2，S3，S4中誤差最大不超過4.65，MWPA反演參數q，tan β，b，θ的中誤差控制在1.08以內，拐點偏移距S1，S2，S3，S4中誤差最大不超過5.34；表明MIWPA穩定性優于MWPA。利用MIWPA反演顧橋礦1414( 1 )工作面概率積分法模型參數為：q＝0.93，tan β＝1.98，b＝0.42，θ＝84.53°，S1＝-12.44 m，S2＝-18.80 m，S3＝55.06 m，S4＝33.98 m。

將MIWPA反演的概率積分法模型參數代入概率積分法模型，計算出的下沉曲線、水平移動曲線分別如圖7，8所示。

圖7 MIWPA工程實例參數估計下沉值擬合情況Fig.7 Parameter estimation subsidence value fitting of MIWPA project example

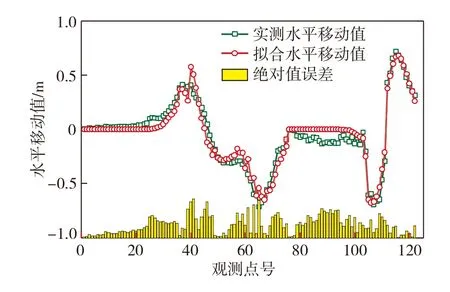
圖8 MIWPA工程實例參數估計水平移動值擬合情況Fig.8 Fitting condition of parameter estimation horizontal moving value of MIWPA project example

由圖7，8可知，下沉值、水平移動值的實測曲線與擬合曲線基本一致，實測值與擬合值間的絕對值誤差均不超過300 mm，下沉與水平移動擬合中誤差為114.88 mm。可見，MIWPA在反演概率積分法模型參數中具有實際應用價值。

4 結 論

( 1 ) 在分析WPA優缺點的基礎上，提出二次游走、改進變異行為策略，形成了改進的WPA( IWPA )，并將IWPA引入概率積分法模型參數反演中，構建了基于改進狼群算法的概率積分法模型參數反演方法( MIWPA )，并編制了工程應用程序。

( 2 ) 通過模擬試驗論證了MIWPA的精確性與可靠性。模擬試驗結果表明：MIWPA反演參數相對誤差、參數中誤差分別不超過3.4%，4.02，滿足工程要求；MIWPA的準確性、可靠性均優于MWPA。

( 3 ) 利用MIWPA對顧橋礦1414( 1 )工作面概率積分法模型參數反演。概率積分法模型參數結果為q ＝0.93，tan β ＝1.98，b ＝0.42，θ ＝84.53°，S1＝-12.44 m，S2＝-18.80 m，S3＝55.06 m，S4＝33.98 m，下沉值與水平移動值擬合中誤差為114.88 mm。