統計學專業數理統計課程研究性教學之初探*
——非正態總體參數的區間估計
姜培華,汪曉云,朱五英
(安徽工程大學數理與金融學院, 安徽 蕪湖 241000)
引言
數理統計是一個有著廣泛應用的數學分支,而參數估計又是數理統計的重要內容之一,它包括點估計和區間估計.與未知參數的點估計相比,區間估計有著明顯的優勢;它不僅給出了參數真值所在的范圍,還給出了該范圍包含參數的可信程度.對于正態總體參數的區間估計問題各類教材都有非常詳盡的介紹,如文獻[1]和[2],但對非正態總體參數的區間估計討論較少.文獻[3]和[4]通過實例介紹了一般總體構造其分布中未知參數區間估計的樞軸量法和分布函數法.文獻[5-7]研究了對一般總體構造其分布中未知參數近似區間估計的方法.文獻[8-10]基于樞軸量法和大樣本方法研究了幾種非正態離散總體參數的精確區間估計和近似區間估計問題.本文對非正態總體構造未知參數區間估計的常用方法進行全面梳理和總結,并通過實例來呈現如何使用這些方法來分析求解未知參數的置信區間,以方便學生系統掌握和教師課堂講授.
1 相關知識
定義1[1]設θ∈Θ是總體的一個參數,(x1,x2,…,xn)為來自該總體的簡單隨機樣本,如果對于給定的
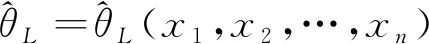
引理1[1]若隨機變量X服從均勻分布,即X~U(0,1),則有
1)隨機變量Y=1-X服從均勻分布,即Y~U(0,1);
2)隨機變量Z=-2lnX服從卡方分布,即Z~χ2(2).
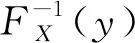
定理1設總體X服從分布F(x,θ),x1,x2,…,xn為來自該總體的簡單隨機樣本,則有
證明因x1,x2,…,xn為來自總體F(x,θ)的簡單隨機樣本,由引理2知:F(xi,θ)~U(0,1),
1-F(xi,θ)~U(0,1),基于引理1再利用卡方分布的可加性可知結論成立.
定理2設總體的密度函數為f(x),xp分為其p分位數,f(x)在xp處連續且f(xp)>0,則當
n→+∞時,樣本p分位數mp的漸近分布為
特別地,對樣本中位數,當n→+∞時,近似地有
此定理的證明可參見文獻[1],這里不再贅述.
2 區間估計的構造方法
2.1 樞軸量法
樞軸量法是構造非正態總體未知參數θ的置信區間的最常用方法之一,下面簡要給出通過構造樞軸量進行區間估計的步驟:
1)設法構造一個樣本和參數θ的函數G=G(x1,x2,…,xn,θ)使得G的分布不依賴于未知參數,一般稱具有這種性質的G為樞軸量.
2)適當地選擇兩個常數c和d,使得對給定的α∈(0,1),有P(c≤G≤d)=1-α成立,在離散場合上式等號改為大于等于.
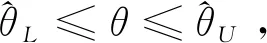
對未知參數進行區間估計的關鍵在于構造合適的樞軸量并確定其所服從的概率分布,然后根據相應的分位數得到所需要的概率表達式.樞軸量的好壞不僅影響求解的速度,更重要的是對置信區間的優良性有著直接的影響.下面通過一些具體實例說明如何選擇一個合適的量來構造樞軸量,進而得到相對優良的置信區間.
例1(基于充分統計量構造樞軸量) 設總體X服從拉普拉斯分布,其密度函數為
其中參數θ未知,求θ的水平為1-α的等尾置信區間.
解: 樣本的聯合密度函數為
對上述分布函數,利用變限積分函數求導可得其密度函數
從而可知
利用卡方分布的可加性可得樞軸量
基于樞軸量G可求得參數θ的1-α水平的等尾置信區間為
例2(基于充分統計量構造樞軸量) 設總體X服從冪分布,其密度函數為
f(x,θ)=θxθ-1,0
其中參數θ未知,求θ的水平為1-α的等尾置信區間.
解: 樣本的聯合密度函數為
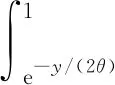
對上述分布函數,利用變限積分函數求導可得其密度函數
從而可知
利用卡方分布的可加性可得樞軸量
基于樞軸量G可求得參數θ的1-α水平的等尾置信區間為
例3(基于順序統計量構造樞軸量) 設總體X的密度函數為
f(x,θ)=e-(x-θ),x>θ,θ∈R.
其中參數θ未知,試求:
1)參數θ的水平為1-α的最短置信區間;
2)參數θ的水平為1-α的等尾置信區間.
解: 1)令yi=xi-θ,i=1,2,…,n,則y1,y2,…,yn獨立同分布于指數分布Exp(1).y(1)的密度函數為
g(y)=ne-ny,y>0.
即x(1)-θ的分布與θ無關,其密度函數為g(y)=ne-ny,y>0,因此可以構造樞軸量G=x(1)-θ來求解置信區間.
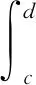
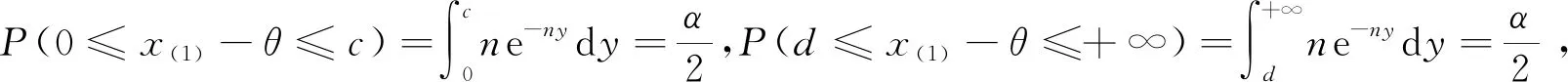
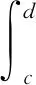
例4(基于順序統計量構造樞軸量) 設x1,x2,…,xn為來自均勻分布U(θ1,θ2)的簡單隨機樣本,記
x(1)≤x(2)≤…≤x(n)為其順序統計量,其中參數θ1,θ2未知,求θ2-θ1的水平為1-α的等尾置信區間.
解: 令yi=(xi-θ1)/(θ2-θ1),i=1,2,…,n,則y1,y2,…,yn獨立同分布于均勻分布U(0,1).首先可以求得(y(1),y(2))的聯合密度函數為
f(y,z)=n(n-1)(z-y)n-2,0 記極差R=y(n)-y(1),則(y(1),R)的聯合密度函數為 f(y,r)=n(n-1)rn-2,y>0,r>0,y+r<1. 于是可求得極差R的邊際密度函數為 從而可知R服從貝塔分布,即y(n)-y(1)~Be(n-1,2),所以有 P(Beα/2(n-1,2)≤y(n)-y(1)≤Be1-α/2(n-1,2))=1-α 樞軸量法求解區間估計的最大困難是如何尋找合適的樞軸量,該方法對概率統計基礎要求較高,技巧性很強,比較靈活,因此構造合適的樞軸量非常困難,可謂是一種挑戰.如果一個統計總體X,其分布函數F(x)有比較簡潔的顯式表達式且僅含有待估的參數,這時利用分布函數法構造區間估計比較有效,會達到“事半功倍”的效果.下面通過實際例子來展示分布函數方法的使用技巧. 例5(基于分布函數法) 設總體X服從冪分布,其密度函數為 f(x,θ)=θxθ-1,0 其中參數θ未知,求θ的水平為1-α的等尾置信區間. 解: 總體X的分布函數為 F(x,θ)=xθ,0 從而可以解出參數θ的1-α水平的等尾置信區間為 例6(基于分布函數法) 設總體X的密度函數為 f(x,θ)=e-(x-θ),x>θ,θ∈R. 其中參數θ未知,求參數θ的水平為1-α的等尾置信區間. 解: 總體X的分布函數為 F(x,θ)=1-e-(x-θ),x>θ,θ∈R. 從而可以解出參數θ的水平為1-α的等尾置信區間為 例7(基于分布函數法) 設總體X服從瑞利分布,其密度函數為 f(x,λ)=2λxe-λx2,x>0,λ>0. 其中參數λ未知,求參數λ的水平為1-α的等尾置信區間. 解: 總體X的分布函數為 F(x,λ)=1-e-λx2,x>0,λ>0. 從而可以解出參數λ的水平為1-α的等尾置信區間為 綜上,對比樞軸量法和分布函數法,不難發現在某些情況下分布函數法和樞軸量法在構造區間估計方面具有一致性,二者是等價的.如例2和例5中關于冪分布參數θ的區間估計問題,樞軸量法和分布函數法最終所得的結果是一致的,但分布函數法明顯優于樞軸量法,簡便易行.在有些場合,分布函數法和樞軸量法所獲得的區間估計具有明顯的不同,區間估計的優劣也有差別.如例3和例6中,樞軸量法是僅依賴于樣本的最小統計量,而分布函數法主要依賴于全樣本. 在有些情形下,尋找樞軸量及其分布比較困難,分布函數法也很難湊效,這時可用漸近分布來構造近似的置信區間,如利用中心極限定理近似、極大似然估計的正態近似和樣本分位數的正態近似等.下面通過實例來說明大樣本近似方法的使用. 例8(中心極限定理近似) 設x1,x2,…,xn是來自泊松分布P(λ)的簡單隨機樣本,其中參數λ未知,求參數λ的水平為1-α的近似等尾置信區間. 此u可作為樞軸量,對給定的顯著性水平α,利用標準正態分布的分位數u1-α/2可得 上述關于λ的二次多項式的二次項系數大于零,故二次函數開口向上,其判別式 故此二次曲線和橫軸有兩個交點,記為λL和λU(λL<λU),則有P(λL≤λ≤λU)=1-α,其中λL和λU可表示為 故參數λ的水平為1-α的近似等尾置信區間為 事實上,上述近似區間是在樣本容量n比較大時使用的,此時有 于是,λ的1-α水平的近似等尾置信區間可進一步簡化為 例9(樣本中位數正態近似) 設總體X的密度函數為 其中參數θ未知,x1,x2,…,xn是來自該總體的簡單隨機樣本,求參數θ的水平為1-α的近似等尾置信區間. 解: 由于柯西分布關于θ對稱,故θ是總體中位數.由定理2可知其樣本中位數近似于正態分布,即 所以有 從而可知參數θ的1-α水平的近似等尾置信區間為 綜上可知,一般在樣本容量足夠大的情況下,根據中心極限定理,非正態總體的抽樣分布與正態總體的抽樣分布差異較小,因此在大樣本條件下,可以把非正態總體問題轉化為正態總體問題,并近似地應用正態總體條件下導出的抽樣分布公式,進而作出各類統計推斷,這就是大樣本統計推斷原理,在區間估計中也遵循這一原則. 總之,非正態總體參數的區間估計一直是數理統計中的一個重點和難點,其處理方法靈活,技巧性強,學生難于掌握.本文系統歸納總結了處理非正態總體參數區間估計的三種常用方法,即樞軸量法、分布函數法和大樣本方法.其中樞軸量法和分布函數法推導給出的置信區間都是精確的,大樣本方法獲得的置信區間都是近似的.通過具體的典型實例展示了使用三種方法構造置信區間的思路和技巧,使學生便于掌握和接受.文中的方法和處理技巧在數理統計研究性教學中值得借鑒和使用,能夠讓學生系統掌握求解非正態總體參數置信區間的常用方法和技巧,并能激發學生的學習興趣和熱情,增強其學習成就感.
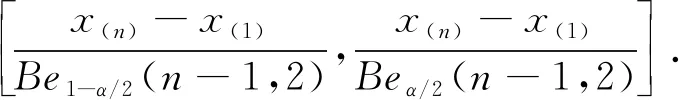
2.2 分布函數法
2.3 大樣本方法
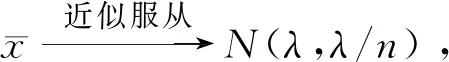
3 結語

