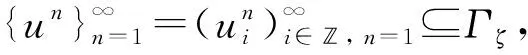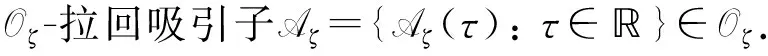一類具變時(shí)滯的Hopfield神經(jīng)網(wǎng)絡(luò)模型拉回吸引子的存在性
朱 雙, 雷 婷
(西南交通大學(xué) 數(shù)學(xué)學(xué)院, 成都 611756)
0 引 言
目前, 關(guān)于Hopfield神經(jīng)網(wǎng)絡(luò)模型[1]動(dòng)力學(xué)行為的研究已有很多結(jié)果[2-6], 關(guān)于不同格動(dòng)力系統(tǒng)吸引子的研究也得到廣泛關(guān)注. 文獻(xiàn)[7-9]證明了二階格動(dòng)力系統(tǒng)吸引子的存在性及收斂性; 文獻(xiàn)[10]考慮非線性時(shí)滯格系統(tǒng), 證明了不存在解唯一性的系統(tǒng)所關(guān)聯(lián)多值過程拉回吸引子的存在性. 本文在文獻(xiàn)[11]的Hopfield神經(jīng)網(wǎng)絡(luò)模型中加入變時(shí)滯項(xiàng), 對(duì)τ∈, 其離散方程為
其中u=(ui)i∈∈l2,μi,γi,λi,j和ζ均為大于0的正常數(shù),n∈,ui,τ為初始值,fj是滿足某些條件的非線性函數(shù),ζ0(t)是時(shí)滯函數(shù),g(t)=(gi(t))i∈是具有時(shí)間依賴性的序列, 并且φi∈C([-ζ,0],). 首先, 證明該方程連續(xù)非自治系統(tǒng)的存在性; 其次, 對(duì)非自治方程的解進(jìn)行一致估計(jì); 最后, 證明非自治方程(1)-(2)拉回吸引子的存在唯一性.
1 解的一致估計(jì)
首先, 定義
其對(duì)應(yīng)的范數(shù)和內(nèi)積分別為
記ut(t∈)為定義在[-ζ,0]上的函數(shù), 其形式如下:
ut(s)=(ui,t(s))i∈=(ui(t+s))i∈=u(t+s),s∈[-ζ,0].

F(u)=-Θu+Υu+G,
其中
則方程組(1)-(2)可寫成如下形式: 對(duì)?τ∈,
為證明問題(3)-(4)拉回吸引子的存在性, 需做如下假設(shè):
(H1)fi(0)=0,fi是全局Lipschitz連續(xù)的函數(shù), 且具有Lipschitz常數(shù)L;
(H2) 存在大于0的常數(shù)a,b,B,d,D, 使得
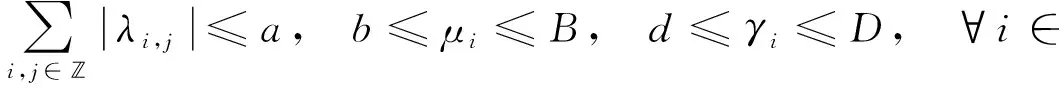
(H3) 令g(t)=(gi(t))i∈, 且


由假設(shè)(H1)~(H3)可知, 算子F:l2→l2是全局Lipschitz連續(xù)的, 且具有Lipschitz常數(shù)L.
顯然, 由泛函微分方程理論可證得對(duì)每個(gè)φ∈Γζ, 均存在T>0, 使得問題(3)-(4)存在唯一的局部解ut(·,τ,φ)∈C([τ,T),Γζ). 因此, 可得:
定理1如果假設(shè)(H1)~(H3)成立, 則對(duì)任意的φ∈Γζ, 存在T>0, 使得問題(3)-(4)存在唯一的解ut(·,τ,φ)∈C([τ,T),Γζ).
引理1如果假設(shè)(H1)~(H4)成立, 則對(duì)任意的τ∈,T>0,φ∈Γζ和t∈[τ,τ+T], 均存在一個(gè)正常數(shù)c=c(τ,T,φ), 使得問題(3)-(4)的解u滿足‖ut(·,τ,φ)‖ζ≤c.
證明: 在空間l2中, 對(duì)方程(3)與u做內(nèi)積, 當(dāng)t>τ時(shí), 得

(5)
由假設(shè)(H2), 得

(6)

(7)
將式(6)~(8)代入式(5), 有

(9)
利用Gronwall不等式, 當(dāng)t>τ時(shí), 有
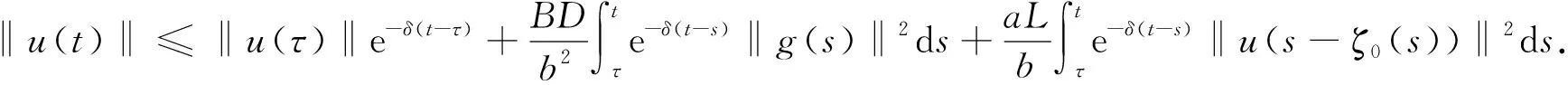
(10)
由假設(shè)(H4), 易知存在正常數(shù)β和Q, 使得當(dāng)‖φ‖ζ≤Q時(shí), 有

(11)
下面證明當(dāng)t≥τ時(shí), 下列不等式成立:
‖u(t)‖≤Qe-β(t-τ)+(1-ρ)-1J(t),
(12)
其中
首先, 證明當(dāng)q>1時(shí), 有
‖u(t)‖ (13) 假設(shè)不等式(13)不成立. 事實(shí)上, 由于‖φ‖ζ≤Q和‖u(t)‖是連續(xù)的, 因此當(dāng)t*>τ時(shí), 必有如下不等式成立: ‖u(t*)‖≥qQe-β(t-τ)+(1-ρ)-1J(t),t≥τ, (14) 且 ‖u(t)‖≤qQe-β(t-τ)+(1-ρ)-1J(t),t≥τ,τ-ζ≤t (15) 所以, 根據(jù)式(11),(12),(14),(15), 有 與式(14)矛盾, 即不等式(13)成立. 其次, 令q→1, 則不等式(12)成立. 證畢. 由引理1可知, 對(duì)任意的T>0, 在區(qū)間[τ,τ+T)上, 問題(3)-(4)的解都是有定義的, 表明局部解u是一個(gè)全局解. 取t∈, 在上定義一個(gè)變換: κt(τ)=τ+t, ?τ∈. (17) 則{κt}t∈作用在上是一個(gè)群. 對(duì)于問題(3)-(4), 定義映射 Π:+××Γζ→Γζ. 取t∈+,τ∈,uτ∈Γζ, 令 Π(t,τ,uτ)=ut+τ(·,τ,uτ), (18) 其中 ut+τ(s,τ,uτ)=u(t+τ+s,τ,uτ),s∈-[ζ,0]. 由解的唯一性可知, 對(duì)任意的t,s∈+,τ∈,uτ∈Γζ, 有 Π(t+s,τ,uτ)=Π(t,s+τ,Π(s,τ,uτ)), 即在Γζ上Π是一個(gè)連續(xù)非自治的動(dòng)力系統(tǒng). 引理2假設(shè)(H1)~(H4)成立, 對(duì)任意的τ∈且, 問題(3)-(4)的解均滿足 (19) 證明: 首先, 在式(9)中分別用ω和τ-t代替t和τ, 則當(dāng)ω>τ-t時(shí), 有 定義函數(shù): Φ(ω)=eβω‖u(ω,τ-t,φ)‖,ω≥τ-t-ζ, (21) (22) 其次, 證明 Φ(ω)≤Ψ(ω),ω≥τ-t. (23) 假設(shè)不等式(23)不成立, 則必有ω*>t-τ, 使得 Φ(ω)<Ψ(ω),ω∈[τ-t-ζ,ω*), (24) Φ(ω*)=Ψ(ω*), 為引導(dǎo)學(xué)生進(jìn)行更加積極有效的討論,課程論壇分為精彩內(nèi)容分享、章節(jié)討論、在線客服三大公共版塊和各班自由討論區(qū)這一班內(nèi)版塊。其中,“精彩內(nèi)容分享”這一版塊主要匯聚了學(xué)習(xí)者的精彩討論內(nèi)容,供學(xué)習(xí)者在學(xué)習(xí)中參考,從而達(dá)到知識(shí)共享、轉(zhuǎn)化和生成的目的;“章節(jié)討論”版塊要求師生討論具體的章節(jié)內(nèi)容或者某一知識(shí)點(diǎn),縮小討論范圍,讓細(xì)節(jié)更加立體,討論更有針對(duì)性,也更為有效;“在線客服”則主要是平臺(tái)技術(shù)人員對(duì)學(xué)習(xí)者在學(xué)習(xí)中遇到的系統(tǒng)問題和對(duì)課程平臺(tái)的建議進(jìn)行及時(shí)解答回復(fù)。 (25) 其中 ω*?inf{ω>τ-t|Φ(ω)>Ψ(ω)}, 并且存在一個(gè)充分小的正常數(shù)Δω, 使得 Φ(ω)>Ψ(ω),ω∈(ω*,ω*+Δω). (26) 計(jì)算Φ(t)在ω*時(shí)的右上導(dǎo)數(shù), 有 根據(jù)式(20), 有 由于在區(qū)間[τ-t-ζ,+∞)上,Ψ(ω)是單調(diào)遞增的, 即根據(jù)式(24),(25), 得 Φ(ω*-ζ0(ω*))<Ψ(ω*-ζ0(ω*))<Ψ(ω*)=Φ(ω*), (29) 因此有 ‖u(ω*-ζ0(ω*),τ-t,φ)‖≤eβζ‖u(ω*,τ-t,φ)‖. (30) 根據(jù)假設(shè)(H1)及式(28),(30)得 (31) 與式(27)矛盾, 即不等式(23)成立. 于是, 當(dāng)t>ζ, -ζ≤ξ≤0時(shí), 有 證畢. 引理3假設(shè)(H1)~(H4)成立, 對(duì)于τ∈和, 存在T=T(τ,)>ζ和M=M(τ), 使得對(duì)任意的t≥T和φ∈, 問題(3)-(4)的解u均滿足 (33) 由假設(shè)(H2), 有 (35) (36) 根據(jù)式(35)~(37)得 (38) 與引理2的證明過程相似, 對(duì)任意的t>ζ和-ζ≤ξ≤0, 有 (39) (40) 再根據(jù)假設(shè)(H3), 存在一個(gè)M=M(τ,ε)>0, 使得對(duì)所有的k≥M, 有 (41) 于是, 由式(39)~(41), 得 (42) 證畢. 引理5如果假設(shè)(H1)~(H4)成立, 則在l2中對(duì)任意的τ∈和)>ζ, 使得問題(3)-(4)的解u滿足uτ(·,τ-t,φ)是等度連續(xù)的. 證明: 定義Pku=(u1,u2,…,uk,0,0,…),u∈l2且k∈. 由引理3可知, 當(dāng)ε>0時(shí), 存在T=T(τ,ε)>ρ和足夠大的正整數(shù)N=N(τ,ε), 使得對(duì)所有的t≥T, 有 (43) 令u1=PNu.對(duì)所有的t≥T, 有 (44) 其中c=c(τ)是一個(gè)正數(shù).不失一般性, 假設(shè)s1,s2∈[-ζ,0], 0 即存在一個(gè)常數(shù)ρ=ρ(ε)>0, 使得如果|s1-s2|<ρ, 則 根據(jù)式(43), 對(duì)所有的t≥T, 有 證畢. 證明: 對(duì)于τ∈, 定義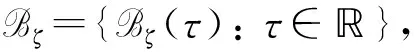








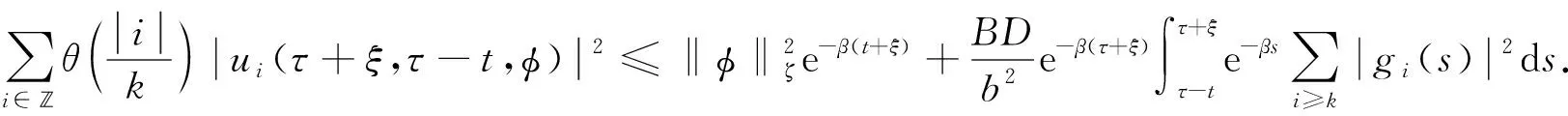
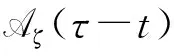


2 拉回吸引子的存在性