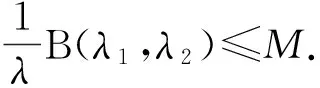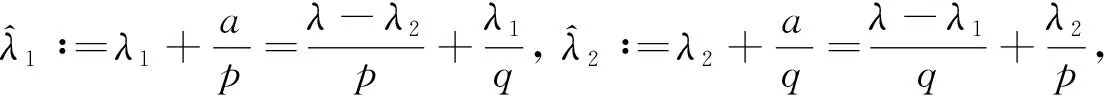具有一個導函數的Hardy-Hilbert型積分不等式
辛冬梅, 楊必成, 閆志來
(1. 廣東第二師范學院 數學學院, 廣州 510303; 2. 廣州中醫藥大學 公共衛生與管理學院, 廣州 510006)
0 引 言


(1)

(2)
這里, 常數因子π仍是最佳值. 不等式(1)和(2)在分析學及其相關領域應用廣泛[2-13].

1 引 理
本文假設p>1, 1/p+1/q=1,λ>0,λi∈(0,λ)(i=1,2),a∶=λ-λ1-λ2,f(x),g(y)是+∶=(0,∞)上的非負可測函數,g(0+)=0,g′(y)≥0 a.e.于+, 滿足條件

引理1對于t>0, 有如下不等式:

(3)
證明: 因為g(0+)=0, 故由分部積分法, 有


即式(3)成立. 證畢.
引理2定義權函數為

(4)

(5)
則有

(6)
ω(λ1,y)=B(λ1,λ-λ1),y∈+,
(7)

即式(6)成立. 同理, 式(7)成立. 證畢.
Γ函數定義為

(8)
對于λ,x,y>0, 可推出

(9)
恒等式Γ(α+1)=αΓ(α)(α>0)及聯系Beta函數的公式

(10)
引理3如下Hardy-Hilbert積分不等式成立:
證明: 由H?lder不等式[25], 有
若式(12)保持等號, 則有不全為0的常數A和B, 滿足

不妨設A≠0, 則存在y∈(0,∞), 使得

與
企業文化自20世紀80年代起逐漸經歷了引進、啟蒙、質問、裂變到整合、本土化的不平凡發展歷程。但時至今日,大多數企業仍未形成成熟的企業文化,往往只注重企業文化的形式,而忽略企業文化的內涵;不能將企業文化精神貫穿于企業經營的過程中,企業行為、員工行為與企業文化嚴重脫節。

(13)
矛盾. 事實上, 對于式(13)左邊, 當a=λ-λ1-λ2∈時, 有x-1-adx=∞. 故由式(8)和式(9)知式(11)成立. 證畢.
2 主要結果
定理1如下具有一個導函數的齊次核Hardy-Hilbert型積分不等式成立:
特別地, 當λ1+λ2=λ(或a=0)時, 式(14)變為
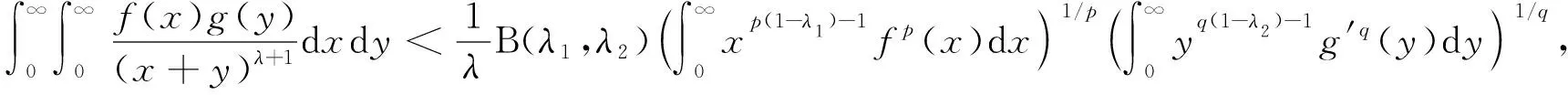
(15)
證明: 由式(9)、交換積分次序的Fubini定理[26]及式(3), 有
再由式(11)有式(14). 當a=0時, 式(14)變為式(15).
對任意的0<ε (17) 可求得 由Fubini定理[26], 又有 把式(18)代入式(17), 有 (19) 在式(19)中令ε→0+, 由Beta函數的連續性, 有 還可將式(14)改寫為如下不等式: (21) 由H?lder不等式[25], 又有 故式(22)保持等號, 即有不全為0的常數A和B, 使得Auλ-λ2-1=Buλ1-1a.e.于+[25]. 不妨設A≠0, 則有于+, 即有a=λ-λ1-λ2=0,λ1+λ2=λ.證畢. 定理3下列結論等價: 3)λ1+λ2=λ; 證明: 1)?2). 由1)及Beta函數的連續性, 有 因此2)成立. 2)?3). 由2)知, 式(22)保持等號, 由定理2的證明結果, 有λ1+λ2=λ. 3)?4). 若λ1+λ2=λ, 則由定理1知, 式(14)的常數因子 是最佳值. 4)?1). 由定理2, 有λ1+λ2=λ, 從而有 B1/p(λ2,λ-λ2)B1/q(λ1,λ-λ1)=B(λ1,λ2), 綜上可知, 結論1),2),3),4)等價. 證畢. 推論1如下具有一個導函數的非齊次核Hardy-Hilbert型積分不等式成立: 特別地, 當λ1+λ2=λ(或a=0)時, 式(23)變為 (24) 在式(25)和式(26)中, 特別地, 取λ=1,r=q,s=p, 則有 取λ=1,r=p,s=q, 則有 當p=q=2時, 式(27)和式(29)變為 (31) 式(28)和式(30)變為 (32) 上述常數因子均為最佳值.