隨機利率下的期權定價
韓 笑, 張敏行
(吉林大學 數學學院, 長春 130012)
Black-Scholes-Merton期權定價模型[1-2]是現代期權定價分析的基礎, 傳統的期權定價模型通常假設市場利率為一個常數, 但這與利率服從隨機過程的金融市場實際情況不符. 基于此, 文獻[3]提出了Vasicek模型, 有效刻畫了具有均值回歸特性的市場隨機利率; 文獻[4]研究表明, 在隨機利率的條件下可通過計價單位轉化推導期權的定價公式; 文獻[5]研究表明, 利用計價單位轉化方法, 可以降維簡化期權定價的偏微分方程.
有限差分法是偏微分方程數值解的一種重要方法. 本文分別采用顯式有限差分法與精度更高的Crank-Nicolson差分法[6], 討論簡化后定價方程的差分迭代格式, 并分別驗證差分格式的穩定性.
1 隨機利率模型


的適應過程, 在風險中性假設下服從如下隨機微分方程:
dr(t)=μ(t,r(t))dt+σ(t,r(t))dWt,
這里μ(·),σ(·)是關于t和r(t)的確定性函數, {Wt,t≥0}是標準Brown運動.
零息債券是一張在到期日T可以獲得1單位現金的債券, 是市場中的一種基本金融產品. 將t時刻零息債券的價值記為P(t), 則P(t)滿足
從而
Vasicek模型[3]很好地刻畫了短期利率的均值回復性, 是目前常用的隨機利率模型. Vasicek模型假設隨機利率服從如下隨機微分方程:
drt=a(b-rt)dt+σdWt,
其中a,b,σ均為正常數. 此時市場上零息債券的價值服從如下反拋物型方程的Cauchy問題:
假設市場上風險資產(例如股票)的價值為S(t), 則S(t)服從如下隨機微分方程:
其中r(t)為市場上的隨機利率,σ1為確定性常數, 刻畫風險資產價值的波動率, {Zt,t≥0}是標準Brown運動, 且
Cov(dWt,dZt)=ρdt.
設t時刻期權的價值為V(t,rt,St), 在風險中性條件下, 歐式看漲期權在t(t≤T)時刻的價值可表示為

根據Faynman-Kac公式可知,V(t,S,r)滿足如下倒向拋物型方程Cauchy問題:

(1)
2 歐式期權定價方程的簡化方法
基于特定的短期利率模型, 文獻[5]研究表明, 如果計價單位選取得當, 則將達到對原有定價方程降維的效果. 本文考慮基于Vasicek隨機利率模型歐式期權價值滿足的偏微分方程, 通過計價單位轉化, 引入新的組合自變量與未知函數, 減少未知函數所依賴的自變量個數, 降低原有的偏微分方程維數, 從而簡化模型方法.

(2)
將上述結果代入式(1), 可得
設
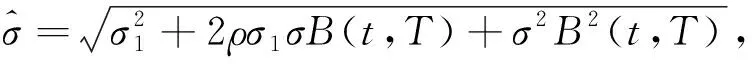
3 Vasicek模型下歐式期權定價方程的差分格式
3.1 顯式差分格式的建立
在Vasicek模型下, 經過降維簡化, 歐式看漲期權的價值服從如下變系數倒向拋物型偏微分方程Cauchy問題:

(3)
方程(3)中的所有系數與終值條件都是充分光滑的. 在區域{0≤y<+∞, 0≤t≤T}上建立如下有限差分網:
Δt=τ,t∈[0,T],
Δy=l,y∈[0,Y].
記分點為(yi,tj), 滿足:
對方程(3)中的偏導數離散化, 則有
代入式(3)可得如下顯式差分格式:
整理得

(4)
差分格式的穩定性表征求解時微小舍入誤差的引入是否會導致解的失真, 收斂性表征差分方程的解是否會收斂到原偏微分方程Cauchy問題的解. 下面討論差分格式(4)的穩定性與收斂性.
定理1在差分格式(4)中, 如果τ,i的選取滿足

(5)
則差分格式(4)具有穩定性.


差分格式的相容性用來衡量差分方程逼近微分方程的程度. 下面利用差分格式的相容性討論差分格式(4)的收斂性.


引理1[7]假設線性偏微分方程定解問題是適定的, 若其差分格式是相容的, 則差分格式的穩定性和收斂性等價, 且誤差階不低于相容階.
定理2如果τ,i的選取滿足式(5), 則差分格式(4)具有收斂性.
證明: 根據定理1, 當τ,i的選取滿足式(5)時, 差分格式(4)具有穩定性. 由引理1, 只需證明差分格式是相容的. 對于
分別將V(yi,tj+τ),V(yi+l,tj),V(yi-l,tj)在(yi,tj)處Taylor展開, 得
從而
表明差分格式是相容的, 且局部截斷誤差為o(τ2+l3). 進一步, 差分格式是收斂的.
3.2 Crank-Nicolson差分格式的建立
Crank-Nicolson差分格式[8-9]是一種更精確穩定的差分格式, 其計算量少于古典隱式差分格式, 且提高了局部截斷誤差的階. Crank-Nicolson格式對方程中的偏導數離散化方法如下:

(6)
將式(6)代入式(3), 得到差分格式:
M1Vi-1=M2Vi,
其中
下面考慮差分迭代格式(7)的穩定性.
引理2[10]如果n×n矩陣A的譜半徑ρ(A)<1,b是任意向量, 則對于任一向量xk, 迭代格式xk=Axk-1+b具有穩定性.
定理3迭代格式(7)具有穩定性.

Vi-1=HVi.
其中H為正規矩陣. 令
|H-λI|=0,
利用奇異值分解的方法[11], 可得其特征值為
矩陣H的譜半徑
由引理2可知, 迭代格式(7)具有穩定性.

