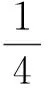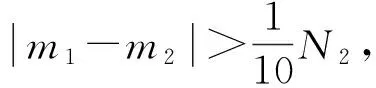Gevrey勢(shì)能的離散擬周期 Schr?dinger算子的非擾動(dòng)Anderson局域化

郭文飛, 陶 凱

(河海大學(xué) 理學(xué)院, 南京 210098)

1 引言與主要結(jié)果

算子譜的局域化問題是數(shù)學(xué)物理領(lǐng)域的熱點(diǎn)問題, 目前已有很多研究成果[1-6]. 文獻(xiàn)[1]考慮如下離散Schr?dinger算子:

(Hx,v,ωφ)=φ(n+1)+φ(n-1)+v(x+nω),n∈,

證明了對(duì)固定的勢(shì)能v, 如果對(duì)所有的Diophantine頻率, 即當(dāng)ω滿足

(1)

本文考慮如下離散Schr?dinger算子:

(3)

(4)

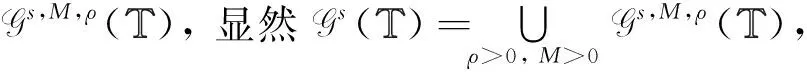
下面給出本文的主要結(jié)果:

2 預(yù)備知識(shí)

首先, 給出Lyapunov指數(shù)的定義[7]. 特征方程Sx,λf+g,ωφ=Eφ可表示為

這里

稱為算子(2)的轉(zhuǎn)移矩陣. 定義

(5)

則由次可加性及Kingman’s次可加遍歷定理知, 極限

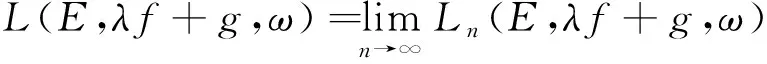
(6)

存在. 式(6)即為Schr?dinger算子的Lyapunov指數(shù).

其中{P1,P2,…,Pk}是d個(gè)變量的多項(xiàng)式集合,

Lj∈{1,2,…,k},kjl∈{>,<,=}.

(7)

同理, 對(duì)于任意正整數(shù)n, 考慮Gevrey函數(shù)g的截?cái)嗪瘮?shù)

(8)

顯然對(duì)任意n, 有

(9)

(10)

結(jié)合式(10)可得

(11)

引理6[7]令I(lǐng)?是一個(gè)大小為N的區(qū)間, 且{Iα}是大小為M?N的子區(qū)間. 假設(shè):

1) 如果k∈I, 則存在α, 使得

[k-M/4,k+M/4]∩I?Iα;

(15)

|GI(m1,m2)|

(16)

(17)

3 定理1的證明

下面分5步給出Anderson局域化的證明.

1) 介紹格林函數(shù)并對(duì)其計(jì)算. 定義

這里R[1,N]是坐標(biāo)約束矩陣, [1,N]∈. 根據(jù)Cramer’s法則知, 存在1≤m1≤m2≤N, 使得

式(18)來自下列MN與行列式的關(guān)系:

(19)

此時(shí)考慮的格林函數(shù)為

則由式(16)可得,

由引理9可知, 存在一個(gè)測(cè)度小于exp{-cN1/(6A)}的集合

(20)

令

mes(B2(E,ω))≤mes(B(E,ω,N1/(6A)))≤exp{-cN1/(6A)}.

(21)

所以有

(23)

(24)

又f,gn是關(guān)于x的最多n8s次多項(xiàng)式, 所以式(24)可記為

P(x,E,ω)≤o(e-N),

(25)

(26)

這里Λ是[1,N],[1,N-1],[2,N],[2,N-1]中之一. 為方便, 本文重新定義Λ是下列間隔之一：

Λ=[-N,N],[-N,N-1],[-N+1,N],[-N+1,N-1].

(27)

特別地, 取n=j, 由式(27)有|j-a|>N/2, |j-b|>N/2, 因此

(29)

令I(lǐng)=[-j0+1,j0-1], 且記

RI(Sx,λf+g,ω(x0)-E)RIφ=-(φ(-j0)e-j0+1+φ(j0)ej0-1),

則

于是

成立, 式中Λ是式(27)其中之一.

(30)

Λ(n)∈{[-N,N],[-N,N-1],[-N+1,N],[-N+1,N-1]},

使得對(duì)m1,m2∈Λ(n), 滿足

(31)

為證明式(30), 只需對(duì)ω做進(jìn)一步的限制. 考慮關(guān)于(ω,E′,x)的集合

其中|j|≤N1,

ω∈Dc,A,

(32)

(33)

(34)

式(32)的作用是確定大偏差定理式(17)在n∈[-NA,NA]上成立. 事實(shí)上, 可以假設(shè)對(duì)所有的ω都滿足式(1), 即

(35)

滿足

(37)

由式(33)可得

det(R[-j,j](Sx,λf+g,ω(x0)-E′)R[-j,j])=0.

P(x,E′,ω)≥0.

(38)

如果N2足夠大(即N足夠大), 則可得

(39)

分割

由式(14)可得

再根據(jù)n和α的選取因素, 可得

5) 定義間隔

(41)

由于φ是廣義特征向量, 故結(jié)合式(28), 有

Sx,λf+g,ω(x0)φ=Eφ, |φn||n|且φ(0)=1,