一種高效的陰陽(yáng)k-Means聚類(lèi)算法

李長(zhǎng)明, 張紅臣, 王 超, 李曉光, 陸 洋, 錢(qián)超越

(1. 長(zhǎng)春光華學(xué)院 工程技術(shù)研發(fā)中心, 長(zhǎng)春 130033; 2. 長(zhǎng)春光華學(xué)院 電氣信息學(xué)院, 長(zhǎng)春 130033; 3. 長(zhǎng)春理工大學(xué) 計(jì)算機(jī)科學(xué)技術(shù)學(xué)院, 長(zhǎng)春 130022)

聚類(lèi)分析是機(jī)器學(xué)習(xí)領(lǐng)域重要的無(wú)監(jiān)督分類(lèi)方法.k-means聚類(lèi)算法具有思想簡(jiǎn)單、收斂性好、易實(shí)現(xiàn)等優(yōu)點(diǎn), 在矢量量化、圖像壓縮和空間數(shù)據(jù)挖掘等領(lǐng)域應(yīng)用廣泛.k-means算法通過(guò)不斷運(yùn)行數(shù)據(jù)分配與中心更新兩個(gè)步驟優(yōu)化目標(biāo)函數(shù)值. 在分配步驟中,k-means算法將每個(gè)數(shù)據(jù)點(diǎn)分配給距離其最近的中心, 這需要計(jì)算所有數(shù)據(jù)與所有中心之間的距離, 計(jì)算復(fù)雜度較高. 針對(duì)該問(wèn)題, 目前已提出了許多加速算法, 其中加速方式分為近似加速和精確加速兩種. 在k-means近似加速領(lǐng)域, Wang等[1]使用多個(gè)隨機(jī)投影樹(shù)建立聚類(lèi)封閉, 提高了k-means算法在分配步驟中的效率和準(zhǔn)確性; Sculley[2]引入了一種小批量采樣方法, 該方法可得到更好的收斂效果, 且在處理高維數(shù)據(jù)集時(shí)不會(huì)增加計(jì)算成本; Hu等[3]提出了一種從粗到細(xì)的搜索方法進(jìn)行多級(jí)過(guò)濾, 測(cè)試數(shù)據(jù)中比標(biāo)準(zhǔn)k-means算法快約600倍； Fahim等[4]提出了一種距離排除準(zhǔn)則, 在連續(xù)兩次迭代中, 點(diǎn)到中心的距離小于上一次迭代的距離, 則可排除剩余的距離計(jì)算, 該準(zhǔn)則適用于大型數(shù)據(jù)集提速; Tsai等[5]利用連續(xù)指定次數(shù)迭代中不變的劃分?jǐn)?shù)據(jù)進(jìn)行加速; Ortegal等[6]通過(guò)計(jì)算中心的移動(dòng)概率確定閥值, 排除了距離計(jì)算； Ortegal等[7]改進(jìn)了該算法, 使用等距閾值改善其在大型數(shù)據(jù)集上的計(jì)算效率. 在k-means精確加速領(lǐng)域, Arthur等[8]通過(guò)選擇具有特定概率的隨機(jī)起始中心提高算法效率; Zhao等[9]在Hadoop平臺(tái)上運(yùn)行k-means算法, 提升了高維數(shù)據(jù)的聚類(lèi)效率; Lai等[10]基于距離不等式與相鄰迭代之間的移動(dòng)距離提出了FKMCUCD算法; Pelleg等[11]提出了一種結(jié)構(gòu)優(yōu)化的方法, 使用k-d樹(shù)簡(jiǎn)化最近鄰查詢步驟, 但當(dāng)維數(shù)大于20時(shí), 該算法的聚類(lèi)效果不理想； Shu等[12]提出了一種Ballk-means算法, 通過(guò)引入球聚類(lèi)和最近鄰聚類(lèi)的思想創(chuàng)建了一種高效且自適應(yīng)的k-means算法； 文獻(xiàn)[13-14]相繼提出了基于三角不等式的算法, 通過(guò)減少點(diǎn)到中心距離計(jì)算加速k-means算法.

Ding等[15]在文獻(xiàn)[13]算法和文獻(xiàn)[14]算法之間進(jìn)行折中, 提出了陰陽(yáng)k-means算法. 陰陽(yáng)k-means 算法屬于精確k-means加速算法, 具有與k-means算法一致的迭代結(jié)果. 其通過(guò)中心分組及引入全局過(guò)濾器、組過(guò)濾器和局部過(guò)濾器排除數(shù)據(jù)與中心之間的距離計(jì)算. 與文獻(xiàn)[13]算法和文獻(xiàn)[14]算法相比, 陰陽(yáng)k-means算法能繼續(xù)加速的前提是能在中心分組下整體進(jìn)行距離排除判定, 與逐個(gè)中心判定相比可節(jié)約大量判斷操作. 但陰陽(yáng)k-means并未利用數(shù)據(jù)的結(jié)構(gòu)關(guān)系進(jìn)行加速. 如果直接采用與陰陽(yáng)k-means中類(lèi)似的中心分組方法進(jìn)行數(shù)據(jù)分組, 由于分組數(shù)據(jù)的分布半徑大于單個(gè)數(shù)據(jù)的分布半徑, 整體判定條件相比于單個(gè)數(shù)據(jù)更難滿足. 當(dāng)整體判定失敗時(shí), 數(shù)據(jù)分組將不再具有優(yōu)勢(shì), 因?yàn)殛庩?yáng)k-means算法無(wú)法繼續(xù)進(jìn)行更細(xì)粒度上的整體判定操作. 針對(duì)該問(wèn)題, 本文在陰陽(yáng)k-means算法的基礎(chǔ)上進(jìn)行改進(jìn), 建立滿m叉樹(shù)將數(shù)據(jù)分組, 以分組后的葉子節(jié)點(diǎn)數(shù)據(jù)建立加權(quán)數(shù)據(jù)進(jìn)行加權(quán)k-means迭代. 由于加權(quán)后數(shù)據(jù)半徑與單個(gè)數(shù)據(jù)半徑相同, 該方法進(jìn)行距離排除判定時(shí)具有比陰陽(yáng)k-means整體判定更高的成功概率, 可以進(jìn)一步提升陰陽(yáng)k-means算法的計(jì)算效率.

1 陰陽(yáng)k-means算法

陰陽(yáng)k-means算法通過(guò)三角不等式原理計(jì)算距離的上下界過(guò)濾數(shù)據(jù)與中心之間的距離計(jì)算, 并通過(guò)移動(dòng)距離進(jìn)行上下界的更新與估計(jì). 設(shè)x為數(shù)據(jù)點(diǎn),C表示聚類(lèi)中心的集合,gi?C(i=1,2,…,k)為中心集合C的一個(gè)分組,b(x)為x的最佳分配聚類(lèi)中心,d(x,b(x))表示x到最佳中心的距離,d(x,c)表示x到c的距離,b(x,gi)表示gi中x的最佳聚類(lèi)中心標(biāo)簽,δ(gi)表示每個(gè)組的最大移動(dòng)幅度,lb(x,gi)表示除b(x)外所有中心之間的最短距離. 陰陽(yáng)k-means算法利用

|d(x,b)-d(b,c)|≤d(x,c)≤d(x,b)+d(b,c)

(1)

進(jìn)行距離過(guò)濾, 其中b,c表示兩個(gè)不同的聚類(lèi)中心. 陰陽(yáng)k-means算法設(shè)置三層過(guò)濾器進(jìn)行距離排除操作. 首先, 進(jìn)行全局過(guò)濾, 對(duì)于每個(gè)點(diǎn)x, 該算法通過(guò)保持上限ub(x)≥d(x,b(x))和全局下限lb(x)≤d(x,c)(?c∈C-b)完成全局過(guò)濾. 其次, 以到最近聚類(lèi)中心的距離作為上界, 到第二近聚類(lèi)中心的距離作為下界進(jìn)行組過(guò)濾. 該步驟將k個(gè)簇分成t個(gè)組G={g1,g2,…,gt}, 其中每個(gè)gi∈G是一組集群, 將t設(shè)為不大于k/10的值. 最后, 將全局過(guò)濾條件應(yīng)用于每個(gè)組. 設(shè)置局部過(guò)濾器, 找到新的b(x), 并利用到第二近中心的距離更新組下限lb(x,gi). 對(duì)于被組過(guò)濾器阻止的組, 用lb(x,gi)-δ(gi)更新下限lb(x,gi), 用d(x,b(x))更新上限ub(x). 在更新步驟利用中心更新公式更新陰陽(yáng)k-means算法的中心.

陰陽(yáng)k-means算法通過(guò)中心分組完成gi內(nèi)所有中心的批量過(guò)濾操作, 如果過(guò)濾成功會(huì)使其比傳統(tǒng)的逐個(gè)中心判定比對(duì)操作計(jì)算量更小. 但其并未利用數(shù)據(jù)結(jié)構(gòu)進(jìn)行加速. 針對(duì)該問(wèn)題, 本文提出一種加權(quán)數(shù)據(jù)的陰陽(yáng)k-means聚類(lèi)算法. 通過(guò)數(shù)據(jù)加權(quán), 既完成了多個(gè)數(shù)據(jù)的統(tǒng)一判定與過(guò)濾操作, 同時(shí), 加權(quán)數(shù)據(jù)本身由一個(gè)數(shù)據(jù)點(diǎn)代表多個(gè)數(shù)據(jù)點(diǎn)并未增大數(shù)據(jù)的半徑, 判定條件易滿足, 可以完成多個(gè)數(shù)據(jù)的同時(shí)判定操作.

2 改進(jìn)陰陽(yáng)k-means算法

2.1 基于滿m叉樹(shù)的數(shù)據(jù)加權(quán)聚類(lèi)

2.1.1 數(shù)據(jù)加權(quán)

圖1 數(shù)據(jù)的分組過(guò)程Fig.1 Process of data grouping

本文用一種加權(quán)數(shù)據(jù)的方法提高陰陽(yáng)k-means算法的速度. 該方法將原始數(shù)據(jù)集F={f1,f2,…,fM}進(jìn)行k-means迭代, 建立滿m叉樹(shù)的數(shù)據(jù)結(jié)構(gòu). 設(shè)樹(shù)的節(jié)點(diǎn)度為m, 深度為h, 則共運(yùn)行(h-1)層標(biāo)準(zhǔn)k-means算法, 第h層葉子節(jié)點(diǎn)的個(gè)數(shù)為m(h-1)個(gè), 樹(shù)的葉子節(jié)點(diǎn)個(gè)數(shù)即為加權(quán)數(shù)據(jù)個(gè)數(shù), 如圖1所示. 本文將最終加權(quán)數(shù)據(jù)個(gè)數(shù)r設(shè)為不大于|F|/10的最大整數(shù).

2.1.2 數(shù)據(jù)加權(quán)聚類(lèi)

本文設(shè)定對(duì)樹(shù)的每個(gè)節(jié)點(diǎn)進(jìn)行3次k-means迭代, 得到加權(quán)后數(shù)據(jù)X={x1,x2,…,xr}與加權(quán)向量W=(w1,w2,…,wr), 再在更新步驟通過(guò)加權(quán)中心更新公式

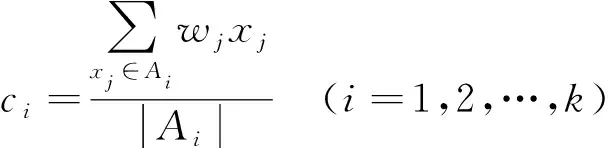
(2)

對(duì)加權(quán)數(shù)據(jù)進(jìn)行陰陽(yáng)k-means迭代. 其中ci表示加權(quán)中心,Ai表示距離中心ci距離最近的所有加權(quán)數(shù)據(jù)點(diǎn)集合.

2.2 中心初始化

本文采用文獻(xiàn)[16]的中心初始化方法.

定義1如果對(duì)于中心cr, dis(p,cr)

圖2 c1和c2是p的有效中心, c3不是p的有效中心Fig.2 c1 and c2 are effetive centers for p, c3 is not an effective center for p

定義2如果中心c不是p的無(wú)效最近中心, 則中心c稱為數(shù)據(jù)點(diǎn)p的有效最近中心.

如圖2所示,c1和c2是p的有效中心. 雖然c3比c1更靠近p, 但是c2導(dǎo)致c3不滿足定義2, 所以c3不是p的有效中心. 有效中心可表示為

(3)

其中dis(p,c)表示下一次迭代中數(shù)據(jù)點(diǎn)p到中心的距離, UNCp表示點(diǎn)p的最近有效中心集合, average(dis(p,c))表示平均距離, max(dis(p,c))表示最大距離.

根據(jù)定義1和定義2為每個(gè)數(shù)據(jù)點(diǎn)建立鏈表, 在每次迭代期間, 根據(jù)式(3)選擇一個(gè)代入值最大的數(shù)據(jù)點(diǎn)作為下一個(gè)中心, 每次迭代后, 將更新每個(gè)數(shù)據(jù)點(diǎn)的“最近有效中心”鏈表, 通過(guò)此方法降低算法對(duì)初始中心的依賴.

2.3 算法流程

1) 利用式(3)初始化聚類(lèi)中心.

3) 將t設(shè)為不大于k/10的值, 并滿足內(nèi)存空間限制. 對(duì)初始聚類(lèi)中心進(jìn)行5次k-means迭代, 將其分為t個(gè)組G={g1,g2,…,gt}.

4) 對(duì)所有加權(quán)數(shù)據(jù)運(yùn)行1次加權(quán)k-means算法, 對(duì)每個(gè)數(shù)據(jù)x, 設(shè)上限為ub(x)=d(x,b(x)), 下限lb(x,gi)為x和Gi中除b(x)外所有中心之間的最短距離(上限和下限分別為距離中心點(diǎn)第一和第二近的距離).

5) 利用式(2)更新中心, 計(jì)算每個(gè)中心的移動(dòng)幅度δ(c), 并記錄每組的最大移動(dòng)幅度δ(gi).

7) 設(shè)置局部過(guò)濾器. 對(duì)于每個(gè)剩余點(diǎn)x, 利用目前找到的第二近的中心過(guò)濾剩余中心, 計(jì)算x到過(guò)濾中心的距離, 找到新的b(x), 并用到第二近中心距離更新組下限lb(x,gi). 對(duì)于未通過(guò)過(guò)濾器的組, 用lb(x,gi)-δ(gi)更新下限lb(x,gi), 用d(x,b(x))更新ub(x).

8) 重復(fù)步驟5)～步驟7), 直到迭代結(jié)束.

9) 再對(duì)原數(shù)據(jù)集F進(jìn)行5次陰陽(yáng)k-means算法的迭代, 得到最終聚類(lèi)結(jié)果.

3 實(shí) 驗(yàn)

3.1 實(shí)驗(yàn)環(huán)境與實(shí)驗(yàn)數(shù)據(jù)

本文實(shí)驗(yàn)的5組對(duì)比數(shù)據(jù)均來(lái)自UCI機(jī)器學(xué)習(xí)數(shù)據(jù)庫(kù), 數(shù)據(jù)集信息列于表1. 實(shí)驗(yàn)環(huán)境為Intel I-54200H 2.8 GHz雙核處理器, Windows10 64位操作系統(tǒng), 8 GB內(nèi)存, VS 2010開(kāi)發(fā)平臺(tái). 所有算法均使用C++語(yǔ)言實(shí)現(xiàn).

表1 5組UCI數(shù)據(jù)集特征

3.2 實(shí)驗(yàn)結(jié)果與分析

實(shí)驗(yàn)分別測(cè)試k-means算法、本文算法、傳統(tǒng)陰陽(yáng)k-means算法(陰陽(yáng)-k)[15]、FKMCUCD算法[10]和Ballk-means (Ball-k)[12]算法的運(yùn)行情況, 結(jié)果列于表2. 以k-means算法的運(yùn)行速度為基準(zhǔn), 用SKM表示k-means算法的速度,Salgm表示其他聚類(lèi)算法的速度,HKM表示k-means算法的函數(shù)值,Halgm表示其他聚類(lèi)算法的函數(shù)值, 則加速比E和函數(shù)值誤差百分比I分別表示為

E=SKM/Salgm,

(4)

I=1-HKM/Halgm.

(5)

表2 不同算法在測(cè)試數(shù)據(jù)集上不同聚類(lèi)個(gè)數(shù)下的運(yùn)行結(jié)果

圖3 4種算法在不同數(shù)據(jù)集上的平均加速比Fig.3 Average speedup of four algorithms on different data sets

由表2可見(jiàn), 只有本文算法與傳統(tǒng)陰陽(yáng)k-means算法在所有測(cè)試條件下加速比均大于1, 表明這兩種算法能在所有測(cè)試條件下加速k-means算法, 具有廣泛的適用性. 加速算法Ballk-means與FKMCUCD在k值較大時(shí)具有較好的加速效果, 對(duì)于某些小k值, 加速比略低. 圖3為當(dāng)聚類(lèi)個(gè)數(shù)為10,20,30,50時(shí)4種算法在UCI數(shù)據(jù)集上的平均加速比. 由圖3可見(jiàn), 在5組UCI數(shù)據(jù)集上, 本文算法的平均加速比始終保持最高, 平均加速比最高達(dá)59.4, 而其他算法的平均加速比最高為8.35. 本文算法的高加速比是因?yàn)楸疚乃惴ㄔ跀?shù)據(jù)加權(quán)聚類(lèi)過(guò)程中, 充分利用了數(shù)據(jù)的結(jié)構(gòu)信息, 用加權(quán)數(shù)據(jù)代替臨近區(qū)域內(nèi)數(shù)據(jù)點(diǎn)集, 大幅度縮減了距離比對(duì)與計(jì)算次數(shù). 通過(guò)數(shù)據(jù)加權(quán), 既完成了多個(gè)數(shù)據(jù)的統(tǒng)一判定與過(guò)濾操作, 同時(shí), 加權(quán)數(shù)據(jù)本身由一個(gè)數(shù)據(jù)點(diǎn)代表多個(gè)數(shù)據(jù)點(diǎn)并未增大數(shù)據(jù)的半徑, 判定條件易滿足, 可以完成多個(gè)數(shù)據(jù)的同時(shí)判定操作.

表2的最后一列為本文算法函數(shù)值誤差百分?jǐn)?shù). 從數(shù)據(jù)結(jié)果可見(jiàn), 在多數(shù)情況下, 本文算法與傳統(tǒng)陰陽(yáng)k-means聚類(lèi)(k-means與陰陽(yáng)k-means算法結(jié)果一致)相比, 函數(shù)收斂精度基本相同或更高. 唯一一組誤差較大的數(shù)據(jù)為Kegg數(shù)據(jù)集, 其函數(shù)值誤差百分?jǐn)?shù)為27.88%～33.22%. 在兩組數(shù)據(jù)Pen-digits與Gas中函數(shù)誤差始終不超過(guò)5.59%, 在LR數(shù)據(jù)集合上多數(shù)結(jié)果誤差不到10%. 在Page數(shù)據(jù)集合上具有比傳統(tǒng)陰陽(yáng)k-means算法明顯更高的收斂精度, 優(yōu)化幅度最高達(dá)284.26%. 測(cè)試精度結(jié)果表明, 雖然利用加權(quán)數(shù)據(jù)代表多個(gè)數(shù)據(jù)點(diǎn)降低了聚類(lèi)的迭代精度, 但利用權(quán)向量進(jìn)行加權(quán)陰陽(yáng)k-means算法迭代在一定程度上克服了數(shù)據(jù)約簡(jiǎn)導(dǎo)致的精度損失, 而且基于加權(quán)結(jié)果采用精確聚類(lèi)迭代進(jìn)一步提高了收斂精度.

綜上所述, 針對(duì)陰陽(yáng)k-means算法聚類(lèi)加速過(guò)程未利用數(shù)據(jù)自身相似性, 計(jì)算效率較低的問(wèn)題, 本文提出了一種基于數(shù)據(jù)多層分解的陰陽(yáng)k-means加速算法. 該算法根據(jù)數(shù)據(jù)相似性建立滿m叉樹(shù)結(jié)構(gòu)逐層分解數(shù)據(jù), 以樹(shù)結(jié)構(gòu)各葉子節(jié)點(diǎn)中存儲(chǔ)的數(shù)據(jù)信息建立加權(quán)數(shù)據(jù), 運(yùn)行加權(quán)陰陽(yáng)k-means算法得到收斂中心. 在原始數(shù)據(jù)中以加權(quán)數(shù)據(jù)收斂中心為初始化條件運(yùn)行陰陽(yáng)k-means算法進(jìn)一步優(yōu)化目標(biāo)函數(shù)值. 與k-means、傳統(tǒng)陰陽(yáng)k-means以及其他加速算法對(duì)比結(jié)果表明, 本文算法在不同數(shù)據(jù)集上始終具有較高的計(jì)算效率, 平均加速比最高達(dá)59.40, 而其他算法的平均加速比最高為8.35. 此外, 在多數(shù)測(cè)試條件下函數(shù)收斂精度誤差不到10%, 與傳統(tǒng)陰陽(yáng)k-means算法精度基本相同.