一種結合Focal Loss 的不平衡數據集提升樹分類算法

朱翌民，郭茹燕，巨家驥，張 帥，張 維

（上海工程技術大學電子電氣工程學院，上海 201620）

0 引言

近年來，不平衡數據集學習成為機器學習領域的研究熱點，其是指一個數據集中某類樣本數量遠小于其他類樣本數量，通常將樣本數量較多的類別稱為多數類（負類），較少的稱為少數類（正類）。由于不平衡數據集中樣本類別分布的不平衡性，使用傳統算法進行分類操作極易導致少數類樣本被多數類樣本“淹沒”，從而使少數類樣本被劃分為多數類。在大數據時代背景下，不平衡數據分類問題在現實中普遍存在，如網絡入侵［1］、電子郵件分類［2］、故障檢測［3］、質量檢測［4］等。針對銀行信用卡系統中存在的欺詐問題［5］，文獻［6］認為這只是眾多交易行為中的冰山一角，正常交易與欺詐交易的數據不平衡問題使得欺詐交易很難被檢測出來，但銀行需要對欺詐事件作出及時響應，以減少財產損失。在醫療診斷領域，先進的儀器和數據采集技術可產生大量醫療數據，但每種疾病在人群中的發生率差異很大，使得數據集極度不平衡，不平衡數據集的處理對于準確診斷病癥十分重要［7-8］。

1 相關工作

針對不平衡數據集分類問題，研究人員提出多種解決方法，主要分為數據重采樣、模型改進與算法適應3 種。數據重采樣即按照某種特定規則濾除數據集中的多數類樣本，或添加少數類樣本，從而使原始數據集達到均衡狀態。最基本的重采樣方法包括隨機欠采樣（RUS）和隨機過采樣（ROS）兩種，但具有遺漏數據集特征和過于強調同一數據的缺點，可能影響分類器性能。為此，很多研究者提出新的重采樣方法，如人工合成少數類過采樣技術（Synthetic Minority Oversampling Technique，SMOTE），其通過對少數類進行分析，選取每個少數類樣本點，在其他少數類中搜索k 個最近鄰樣本，并以0～1 之間的采樣倍率進行線性插值，從而產生新的合成數據。改進形式的SMOTE 使用每個少數類的歐氏距離調整類別分布，從而在其余少數類樣本附近合成新的少數類樣本［9］。例如，文獻［10］中的Broder?line-SMOTE 算法采用最近鄰原則將少數類分為safe、dan?ger、noise 3 種類型，僅在danger 類型的少數類樣本中合成新的少數類樣本；文獻［11］中的A-SMOTE 算法根據與原始少數類樣本的距離調整新引入的少數類樣本，向少數類中引入新樣本，并消除比少數類更接近多數類的示例；文獻［12］利用不平衡三角形合成數據（Imbalanced Triangle Synthetic Data Method，ITSD）彌補SMOTE 線性插值的不足，在數據集特征空間的分類超平面兩端取3 個數據點構成不平衡三角形，最大限度地利用了少數類和多數類數據。

模型改進策略則盡可能地保留原始數據的分布特征與數據集的內在結構，通過調整傳統分類算法或優化現有分類思想，使其適應不平衡數據集的內在特征，從而提高對少數類樣本的識別能力。例如，文獻［13］通過聚類算法對數據集進行均衡處理，然后采用AdaBoost 算法進行迭代獲得最終分類器；文獻［14］通過改進的貝葉斯分類模型將貝葉斯思想引入不平衡分類任務，用類別的間隔似然函數代替后驗分布中樣本的概率似然函數，優化了分類判別依據，提高了不平衡數據的分類精度。在深度學習領域也有模型改進策略的提出，如Lee 等［15］提出利用經驗模態分解能譜數據，然后通過GAN 生成新樣本，得到了比傳統過采樣技術更好的分類效果；魏正韜［16］提出對采樣結果增加約束條件，削弱采樣對類別不平衡的影響，在保證算法隨機性的同時利用生成的不平衡系數對每個決策樹進行加權處理；劉耀杰等［17］在構造隨機森林算法過程中對處于劣勢地位的少數類賦予較高的投票權重，從而提高了少數類樣本的識別率。

算法適用則是融合多種方法優點，使其訓練出的分類器具有更好的多元性和魯棒性，代表性算法包括SMOTEBoost［18］、XgBoost［19］、AdaBoost［20］等。

上述文獻主要研究了樣本數量不平衡的問題，對難易樣本的不平衡問題沒有進行深入討論。在模型訓練中，如果一個樣本可以很容易地被正確分類，這個樣本對于模型來說即為易分樣本，但模型很難從易分樣本中得到更多信息。而被分錯的樣本對于模型而言為難分樣本，其產生的梯度信息更加豐富，更能指導模型的優化方向。在實際訓練過程中，雖然單個易分樣本損失函數很小，單個難分樣本損失函數較大，但由于易分樣本占整個數據集的比重極高，易分樣本累積起來的損失函數仍會主導損失函數，導致模型訓練效率非常低，甚至會出現模型退化問題。因此，本文針對難易樣本不平衡問題，提出在提升樹模型的基礎上結合Focal Loss 損失函數的分類算法，通過Focal Loss 損失函數調整易分樣本和難分樣本在損失函數中的權重，使模型訓練更關注于難分樣本。在UCI 和KEEL 數據庫中對建立的新算法與Borderline-SMOTE 結合梯度提升樹的算法進行了比較，發現新算法雖然對分類精度的提升效果有限，但收斂速度明顯提升。

2 算法介紹

2.1 Focal Loss

在目標檢測問題中，每張圖片可能產生上萬個目標候選區，但通常只有少數候選區中含有需要識別的對象，其余部分均為圖片背景內容，這便導致了類別不平衡問題。此外，負樣本大多是容易分類的，會使模型優化方向背道而馳［21］。使用Focal Loss 損失函數，通過減少易分類樣本的權重，使模型在訓練時更專注于難分類樣本，以達到更高的分類準確率。

對于一般的二分類問題，單樣本(x,y)的交叉熵損失函數為：

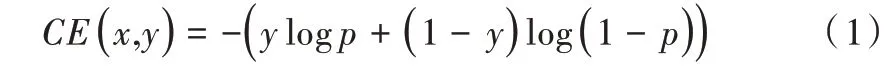
式中，y∈{ 0,1} 為類別標簽，p∈[ 0,1 ]為預測樣本屬于類別1 的概率。

對于不平衡數據集的分類問題，可采用調整多數類和少數類樣本權重的方式提高模型對少數類樣本的分類效果，表達為：

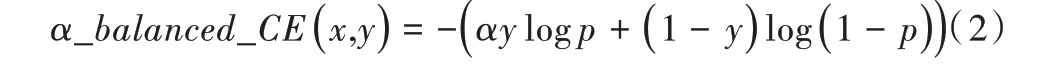
Focal Loss 損失函數調整了易分樣本在損失函數中的權重，表達為：

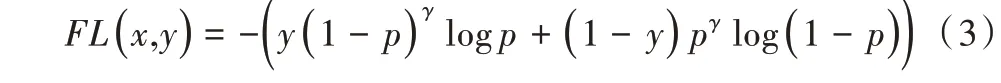
式中，γ為調節系數。對比交叉熵損失函數可以看到，Focal Loss 可在訓練過程中動態調整易分樣本與難分樣本在損失函數中的權重。

2.2 提升樹

提升樹是一種Boosting 算法，采用的基函數為決策樹的加法模型，通過前向分布算法獲得新的弱學習器，將每一步的回歸樹組合起來，即可得到滿足需求的強學習器［22］。

當損失函數取平方差損失和指數損失時，每一步迭代的優化都相對簡單。但對于一般損失函數而言，每一步的優化通常較難計算。針對該問題，Freidman［23］提出梯度提升算法，通過損失函數的負梯度在上一步迭代得到的學習器下的值擬合回歸樹。

3 結合Focal Loss 的不平衡數據集提升樹分類算法原理與步驟

一般情況下，在分類模型任務中，模型性能的優劣與數據集中各類別樣本的分布特性有很大關系。在不平衡數據集中，可以根據正負、難易兩種標準將樣本分為4 種類型，分別為易分正樣本、難分正樣本、易分負樣本、難分負樣本。采用梯度方法訓練模型時，雖然每個易分樣本產生的梯度均較小，但由于數量較多，最終還是會主導梯度更新方向。在提升樹中引入Focal Loss 損失函數，降低易分樣本在訓練中的權重，使其更關注能有效指導模型優化方向的難分樣本，從而提高算法的收斂速度。此外，由于難分負樣本占所有負樣本的比例較小，可降低樣本的不平衡程度，一定程度上提高不平衡數據集的分類準確率。

為得到提升樹中葉子結點每次迭代更新的權值，假設輸入為x，二分類問題的標簽為y∈{ 0,1}，提升樹分類模型為，第m 輪迭代時學習到的提升樹基函數為，則學習 到的提升樹為：

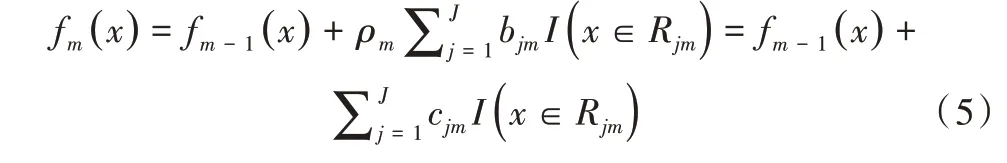
通過牛頓法可得到式（5）的近似解，即葉結點的權值為：

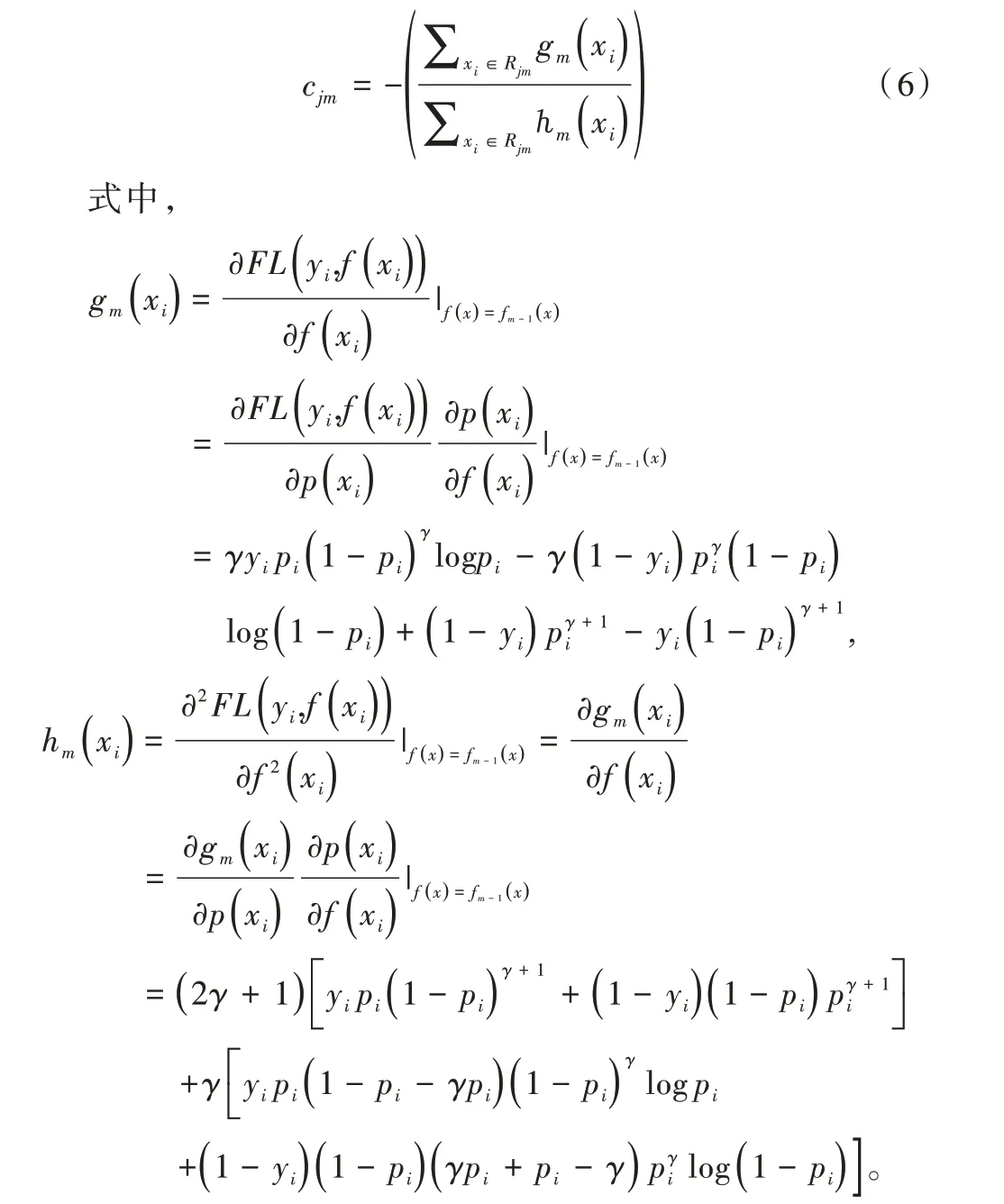
根據上述計算，得到本文算法的具體步驟如下：

b）更新每個葉結點的輸出值cjm；

（3）最終的提升樹為fM(x)。

4 實驗結果與分析

為驗證該模型的有效性，選擇來自不同領域的3 組數據集，與Borderline-SMOTE 以及隨機森林算法進行比較。實驗硬件環境：Win10 系統、16GB 內存以及Core i5 處理器；軟件環境：Python3.7。

4.1 數據集

使用來自UCI 與KEEL 數據庫的3 組數據，數據集具體信息如表1 所示。其中Number 表示數據集的樣本總數，At?tributes 表示樣本特征數量，Minor/Major 表示正類/負類，IR表示數據集的不平衡度。

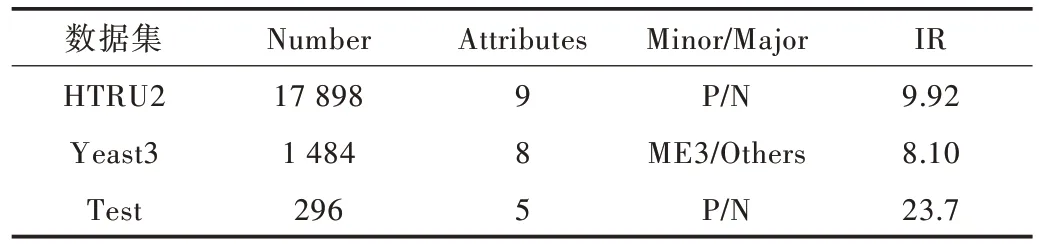
Table 1 Dataset information表1 數據集信息

4.2 評價指標

在不平衡數據分類中，單純使用準確度評估算法的優劣已不再適用。當數據集的不平衡率較高時，即使將正類樣本全部預測為負類，分類器仍然可以獲得很高的預測準確度。因此，本文采用查全率（recall）、查準率（precision）、F1-score 和G-mean 4 個性能度量指標對模型進行評估。以上指標可根據表2 所示的混淆矩陣得到，具體表達如式（7）—式（10）所示。

Table 2 Confusion matrix表2 混淆矩陣

查全率（Recall）計算公式為：

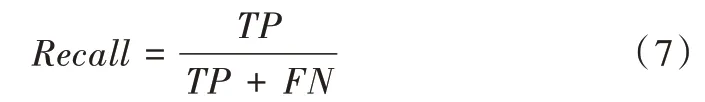
查準率（Precision）計算公式為：

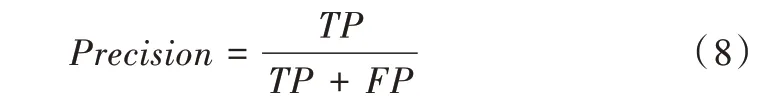
F1-score 計算公式為：

G-mean 計算公式為：

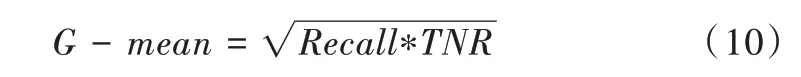
4.3 算法結果比較分析

采用十折交叉驗證方法，將數據隨機分為10 等份，取9份作為訓練集，1 份作為測試集，依次進行實驗，10 次實驗評價指標的平均值作為1 次十折交叉驗證的最終結果。

通過調整Focal Loss 損失函數中的γ值，可以動態調節易分樣本與難分樣本在損失函數中的權重，從而使模型更專注于難分樣本。圖1、圖2 分別為在數據集HTRU2、Yeast3 上，不同γ值下訓練損失隨迭代次數的變化情況。可以看到，隨著γ值的上升，模型收斂速度明顯加快。由圖1 可知，當γ=2 時，數據集HTRU2 在第13 次迭代就接近收斂；當γ=1 時，需要約16 次迭代；當γ=0 時，則需要20 次以上迭代才逐漸收斂。由圖2 可知，當γ=2 時，數據集Yeast3 只需要14 次迭代便接近收斂；當γ=1 時，需要20 次迭代；當γ=0 時，則需要20 次以上迭代才逐漸收斂。

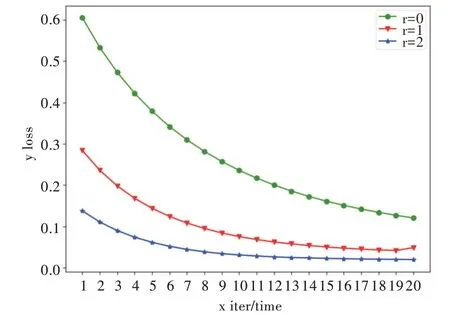
Fig.1 Change of training loss with the number of iterations under different γ（HTRU2）圖1 不同γ 值下訓練損失隨迭代次數的變化（HTRU2）

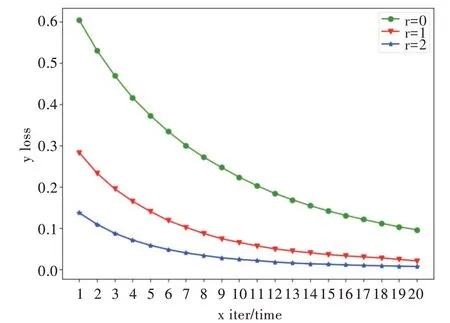
Fig.2 Change of training loss with the number of iterations under different γ（Yeast3）圖2 不同γ 值下訓練損失隨迭代次數的變化（Yeast3）

在數據集HTRU2 和Yeast3 上改變Focal Loss 的調節參數γ，采用Recall、Precision、F1-score 和G-mean 4 個指標評價不同γ 值下的分類器性能，實驗結果如表3 所示。Test 數據集的數據量過少，很容易產生過擬合，因此并沒有加入對照。采用Borderline-SMOTE 結合隨機森林的分類算法作為對比，首先對不平衡數據集進行過采樣，獲得平衡數據集后再使用隨機森林進行分類，實驗結果如表4 所示。本文算法在Recall、Precision 和F1-score3 個指標上表現較佳，但與對照算法相比優勢并不顯著。在HTRU2 數據集上，本文算法F1-score 最佳值為0.970，而Boderline-SMOTE結合隨機森林算法的F1-score 為0.972，相差甚微。因此，單純改變模型中參數γ的值對分類效果的提升有限。

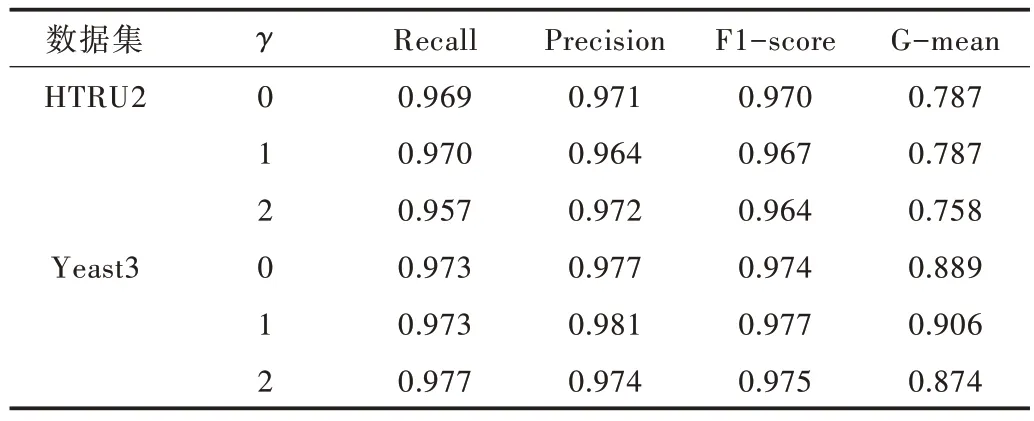
Table 3 Classification results of established algorithm under different γ表3 不同調節參數γ 下本文算法分類結果

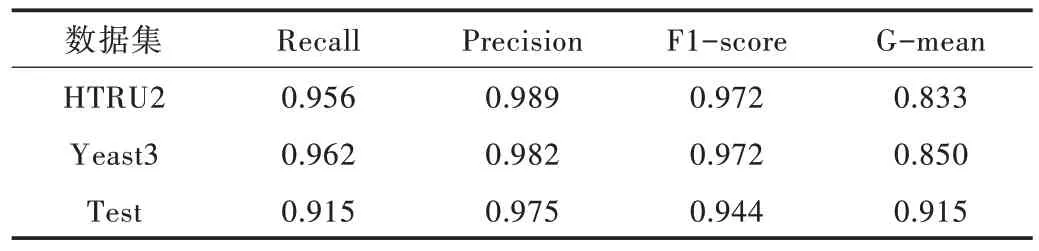
Table 4 Classification results of Boderline-SMOTE with gradient boosting tree表4 Boderline-SMOTE 結合梯度提升樹分類結果

5 結論

針對分類任務中的類別不平衡問題，本文提出結合Fo?cal Loss 損失函數的梯度提升樹算法，在數據集上進行驗證實驗后發現調整權重γ值可大幅提高算法的收斂速度，但對不平衡數據集分類效果的提升較為有限。后續可嘗試在損失函數中加入平衡因子以提升算法的性能。此外，本文主要討論了二分類問題，今后可針對多分類問題進行探討。