基于子空間K 均值聚類的概率配準算法

陳 璐，汪亞明，韓永華

（1.浙江理工大學 信息學院，浙江 杭州 310018；2.麗水學院，浙江 麗水 323020）

0 引言

點集配準問題是計算機視覺廣泛研究的問題，開發(fā)準確的點集配準算法一直都是模式識別領(lǐng)域研究熱點［1］。點集配準目標是尋找兩組相關(guān)點集之間的對應(yīng)關(guān)系，或恢復兩組點集之間的轉(zhuǎn)化關(guān)系，從而建立兩個點集之間的一一映射。根據(jù)變換方式不同，可將配準問題分為剛性配準問題和非剛性配準問題兩類。剛性配準的變換方式僅考慮平移、旋轉(zhuǎn)和比例縮放。非剛性配準變換方式通常較復雜，難以建模，包含較多的變換參數(shù)。在現(xiàn)實世界中，很多問題會涉及到非剛性變換，即面臨非剛性配準問題，非剛性配準因為變換模型的未知以及存在大量的變換參數(shù)而更具挑戰(zhàn)性。

目前，剛性點集配準研究已取得一定成果，迭代最近點（Iterative Closest Point，ICP）算法及它的變體是使用最廣泛的方法之一［2］。該算法迭代地建立最近鄰點對之間的對應(yīng)關(guān)系并最小化點對距離，但由于其假設(shè)目標點集和源點集之間的最近點對相互對應(yīng)而存在局限性，而算法的收斂性和準確性很大程度上取決于給定點集的相似性，因此易陷入局部極小值；Gold 等［3］為防止陷入局部極小值，提出一種用于確定空間中兩個點集的姿態(tài)和對應(yīng)關(guān)系的魯棒點匹配（Robust Point Matching，RPM）算法。該算法應(yīng)用一種確定性退火方法來凸化它們的能量函數(shù)，但RPM 算法僅限于仿射和分段仿射映射；由Chui 等［4］開發(fā)的薄板樣條魯棒點匹配（Thin Plate Spline Robust Point Matching，TPS-RPM）算法試圖解決RPM 和ICP 算法中固有的非剛性映射問題，提出一個通用框架來解決存在異常值和噪聲的非剛性配準問題；之后，Myronenko 等［5］提出在剛性和非剛性轉(zhuǎn)換下都能夠配準點集的概率方法，稱為一致性點漂移（Coher?ent Point Drift，CPD）算法。該算法通過估計概率密度函數(shù)優(yōu)化對齊兩個點集，通過最大化似然函數(shù)尋找最優(yōu)變換參數(shù)，迭代地將源點集的質(zhì)心與目標點集數(shù)據(jù)進行擬合［6］。同時，為了保持點集的全局拓撲結(jié)構(gòu)，將中心點作為一個整體進行移動。但CPD 算法中有一個權(quán)值參數(shù)w 用來預測GMM（Gaussian Mixture Model，GMM）中的噪聲水平和異常值數(shù)量，是在不明確的約束條件下人工選擇的；為了解決這一問題，Wang 等［7］引入一種自動選擇w 最優(yōu)值的算法；另外，為了解決CPD 算法只考慮點集全局結(jié)構(gòu)的局限性，Yang 等［8］提出全局和局部距離薄板樣條（Global and local distance thin plate spline，GLMDTPS）非剛性點集配準算法。該算法基于全局和局部特征進行對應(yīng)關(guān)系評估，全局和局部特征通過確定性退火技術(shù)融合為混合特征；在Ge 等［9］提出的全局—局部拓撲保持（Global-Local Topology Preserva?tion，GLTP）算法中，增加了一種局部描述符，稱為局部線性嵌入（Local Linear Embedding，LLE），以保持兩個點集之間的局部結(jié)構(gòu)。在概率非剛性配準算法中，一個常見的問題是不準確的對應(yīng)估計很容易導致優(yōu)化過程陷入局部最優(yōu)。

針對非剛性配準算法準確性較低問題，本文提出一種基于聚類的概率配準算法。該算法在基于GMM 的CPD 算法的配準框架下，在初始階段對點集聚類，將聚類中心的對應(yīng)關(guān)系投影到兩個點集的對應(yīng)關(guān)系，最后將配準框架結(jié)合局部拓撲保持得到最終配準結(jié)果。基于GMM 的點集配準算法目標是對齊兩個高斯混合函數(shù)并優(yōu)化它們之間的統(tǒng)計差異。當前先進的點集算法大多基于GMM［10-11］，原因有3 個：①現(xiàn)實問題可以有效地建模為GMM；②GMM 更容易解釋和表達；③低維點集存在閉式解，從而使算法的效率更高。另外，由于本文提出的算法通過聚類大量減少了初始配準點集數(shù)量，從而提高了配準速度，與此同時保持了局部拓撲結(jié)構(gòu)，使配準具有收斂更快、精度更高等特點。

1 基于聚類的概率配準算法

基于聚類的概率配準算法研究關(guān)鍵是通過將聚類投影和局部拓撲保持融合到基于高斯混合模型的概率配準框架中，從而解決點集配準算法中準確性不足的問題。首先對兩個給定點集分別進行聚類，對聚類中心進行配準，之后將聚類中心的對應(yīng)關(guān)系投影到點集中，最后進行局部結(jié)構(gòu)保持的配準。下面先介紹通用的基于高斯混合模型的點集配準框架，在此基礎(chǔ)上給出聚類對應(yīng)投影方法，最后介紹局部結(jié)構(gòu)拓撲保持。

1.1 基于高斯混合模型的點集配準框架

基于高斯混合模型的點集配準框架將兩個點集的對齊問題視為概率密度估計問題，其中一個點集表示高斯混合模型的各個分模型，即高斯模型的均值，另一個點集表示為數(shù)據(jù)點，通過不斷重置質(zhì)心位置進行配準。

給定兩個點集XN×D=(x1,…,xn,…,xN)T，YM×D=(y1,…,ym,…,yM)T，D是點集中點的維數(shù)，N是X點集的點個數(shù)，M是Y點集的點個數(shù)。點集Y中的點作為GMM 的均值，點集X中的點作為GMM 生成的數(shù)據(jù)點。每個GMM 分模型的概率密度為：

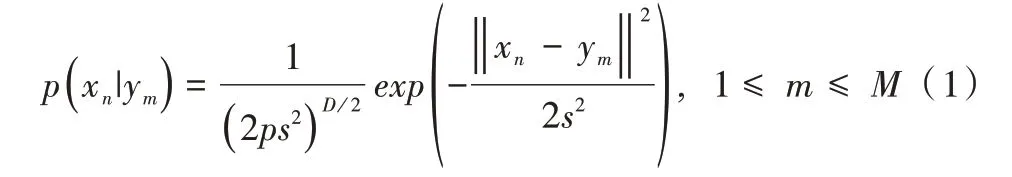
假設(shè)所有的高斯分量獨立分布且具有相同的方差，并且對每個分量的概率相同。考慮到數(shù)據(jù)中存在噪聲和異常值，在混合模型中引入一個額外的均勻分布p(x|M+1)=。此時，點xn的GMM 概率密度函數(shù)為：

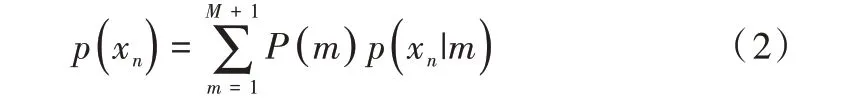
結(jié)合兩種概率分布，使用參數(shù)ω（0 ≤ω≤1）對兩種分布進行加權(quán)，則混合模型的概率密度函數(shù)為：

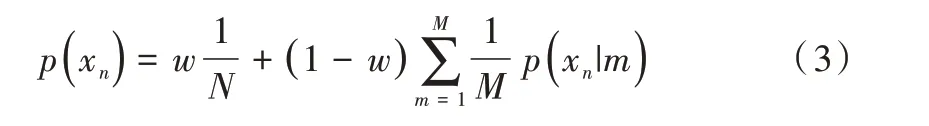
點集配準利用最小負對數(shù)似然函數(shù)方法不斷重置GMM 的均值，此時方差也隨著均值位置的改變而發(fā)生變化。設(shè)θ為GMM 均值改變的轉(zhuǎn)換參數(shù)，則負對數(shù)似然函數(shù)可以寫作：

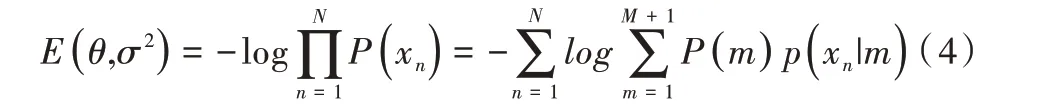
通過最大期望（EM）算法計算得到所需要的參數(shù)(θ,σ2)，使負對數(shù)似然函數(shù)達到最小。

將ym和xn兩點之間的關(guān)聯(lián)系數(shù)定義后驗概率：

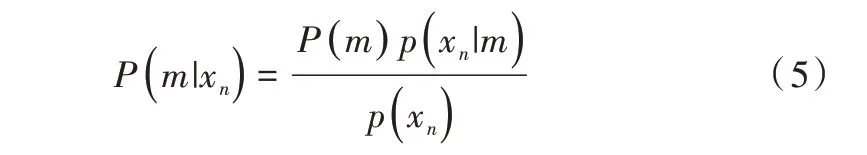
求解Pold(m|xn)就是EM 算法的E-step，M-step 利用求得的后驗概率求解新的參數(shù)值使目標函數(shù)Q最小化［12］，即：

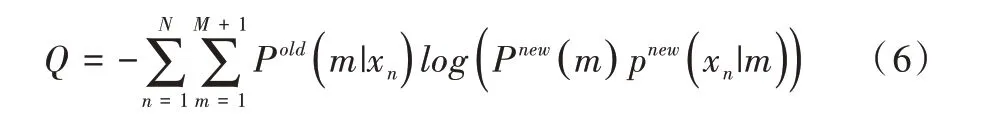
EM 算法在E-step 和M-step 之間交替進行，直到收斂。

根據(jù)概率密度函數(shù)，可以將目標函數(shù)改寫為與參數(shù)相關(guān)的形式，即：

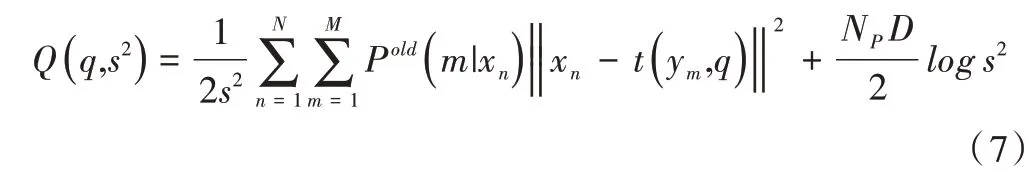
后驗概率密度函數(shù)為：

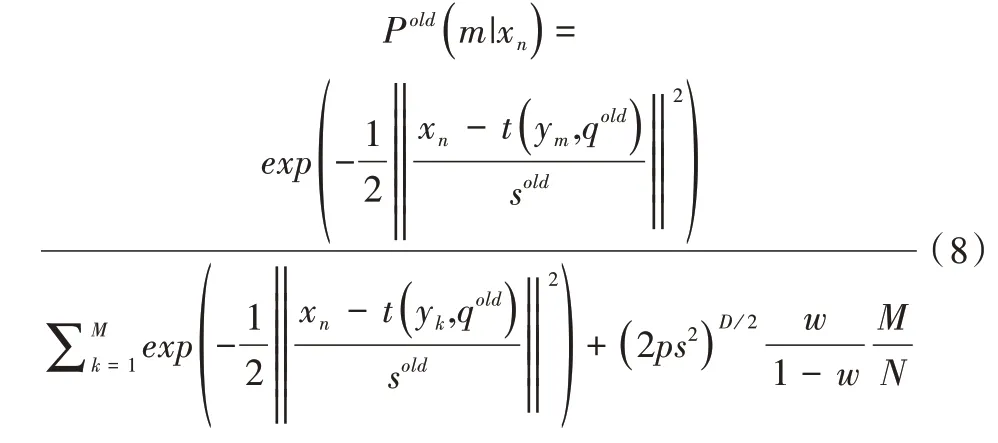
后 驗概率矩陣PM×N正是對應(yīng)關(guān)系矩陣，矩陣PM×N中每個元素代表ym和xn兩點之間的關(guān)聯(lián)系數(shù)。

1.2 聚類及聚類對應(yīng)投影

當兩個點集基數(shù)變大、點對應(yīng)矩陣的維數(shù)變大時，點對應(yīng)關(guān)系的求解效率就會變低。所以先通過聚類尋求問題的近似解。主要思想是將兩個點集分別聚類，用兩個點集的聚類中心之間的對應(yīng)關(guān)系替代兩個點集之間的對應(yīng)關(guān)系，從而用聚類中心對應(yīng)投影問題代替點對應(yīng)投影問題［13］，最后將聚類對應(yīng)投影結(jié)果轉(zhuǎn)換回點對應(yīng)。

經(jīng)實驗，在各種聚類算法中，子空間K 均值聚類［14］配準精度更好，因此本文運用子空間K 均值聚類算法將X點集聚類成a個簇，表示為，將Y 點集聚類成b個簇，表示為。另外，用xk表示X點集中k簇的聚類中心，用yl表示Y點集中l(wèi)簇的聚類中心。對兩個點集進行聚類之后，對聚類中心進行配準，此時，概率密度函數(shù)為：

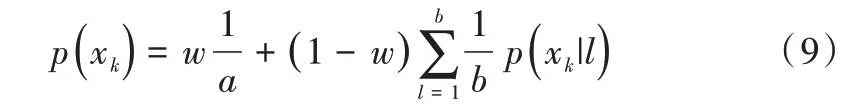
配準之后得到一個矩陣Qk×l，表示兩個點集中聚類中心之間的對應(yīng)關(guān)系。qk,l為矩陣Q中的元素，即表示X點集中與Y點集中的對應(yīng)關(guān)系。

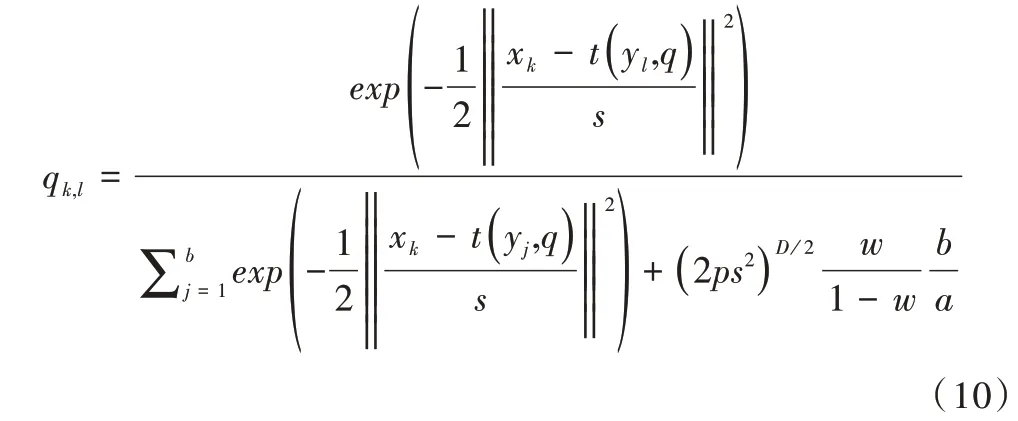
如果點對應(yīng)P滿足點對應(yīng)矩陣P的約束CP，如，pij≤1,pij≥0，則對P的簇內(nèi)元素求平均，形成聚類中心對應(yīng)的Q滿足聚類對應(yīng)矩陣Q的約束CQ，如1 ≤k≤a,1 ≤l≤b；反之，如果聚類中心對應(yīng)Q滿足聚類對應(yīng)矩陣Q的約束CQ，則Q的元素在相應(yīng)簇中復制形成的點的對應(yīng)P也滿足點對應(yīng)矩陣P的約束CP，所以在配準算法中可以通過復制聚類中心對應(yīng)的中的元素來構(gòu)造點對應(yīng)P，即，達到聚類對應(yīng)矩陣Q投影到點對應(yīng)矩陣P的效果。

1.3 拓撲結(jié)構(gòu)保持

由聚類對應(yīng)投影得到點集之間的對應(yīng)之后，在基于高斯混合模型的點集配準框架中加入局部結(jié)構(gòu)拓撲保持對兩個點集進行更精確的配準。

對于非剛性點集數(shù)據(jù)的配準問題，定義變換關(guān)系τ(Y,v)如下：

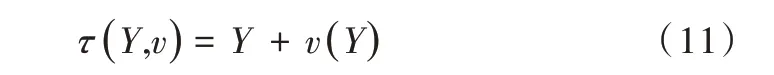
其中，Y表示Y點集的初始位置，v表示位移函數(shù)。在非剛性變換情況下，由于沒有適當?shù)恼齽t化，配準通常面臨不適應(yīng)問題。運動相干理論（MCT）認為，相鄰的點具有相干運動的傾向，因此點集之間的位移函數(shù)應(yīng)該是平滑的。因此，在再生和希爾伯特空間（RKHS）［15］中建立位移函數(shù)v的模型，空間平滑正則化定義為v的傅里葉域范數(shù)，記為。

將定義的變換及正則化項加入到目標函數(shù)中，得到：

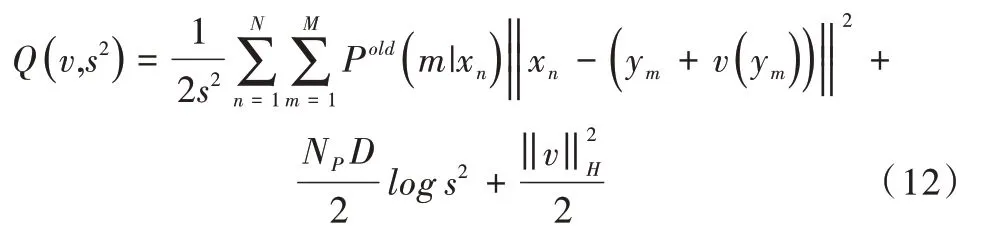
以點集Y為中心的特定核函數(shù)K的線性組合，給出使目標函數(shù)最小的最優(yōu)函數(shù)v，即：

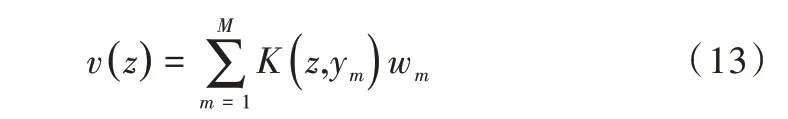
其中，z是點集Y中的一點，wm是待確定的系數(shù)向量。通過選擇高斯核函數(shù)使正則化等價于運動相干理論（MCT），得到Y(jié)的變換位置為：

其中，GM×M為核矩陣，WM×D為核的權(quán)重矩陣。核矩陣中第i行，第j列的元素表示為，1 ≤i≤M，1 ≤j≤M，β控制局部平滑數(shù)量的高斯核大小。

然后對權(quán)值矩陣W 進行正則化，以增強運動一致性，并相應(yīng)地保持全局拓撲：

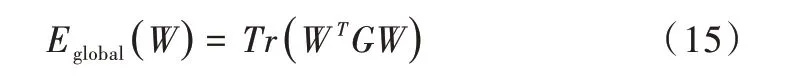
其中tr(·)表示矩陣的跡。保持全局拓撲使得所有的點作為一個整體一起運動。通過這種方式來保持點集的全局拓撲結(jié)構(gòu)，可以保留不同部分的連通性和結(jié)合度。

全局拓撲有助于在配準期間保持點集的整體空間連接性，但可能不足以處理詳細的局部變形。因此，在保持全局結(jié)構(gòu)的同時還需要保持局部鄰域結(jié)構(gòu)并適應(yīng)不同的局部變形，且能與基于高斯混合模型的概率配準框架相結(jié)合，起到互補作用。局部線性陷入（LLE）算法［16］作為一種非線性降維方法在低維潛在空間中保持局部鄰域結(jié)構(gòu)。局部結(jié)構(gòu)表示為每個頂點與其預先選定的最近鄰之間的空間關(guān)系。從高維到低維的映射中，通過共享同一組局部線性重建系數(shù)來保持局部結(jié)構(gòu)。

配準時希望Y點集的局部結(jié)構(gòu)經(jīng)過非剛性變換后仍能保留，應(yīng)用LLE 思想進行非剛性配準。首先，根據(jù)歐氏距離計算Y點集中每個點的K個最近鄰；其次，將Y點集中的每個點用其相鄰點的加權(quán)線性組合表示，通過使成本函數(shù)最小化得到權(quán)值，成本函數(shù)為：

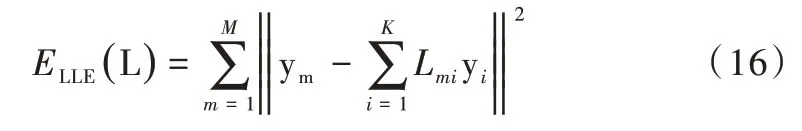
其中矩陣LM×K包含Y點集中每個點的領(lǐng)域信息。

最后由式（16）中定義的權(quán)重矩陣W控制非剛性變換后，計算具有相應(yīng)權(quán)值的所有點的總重構(gòu)誤差。為得到最優(yōu)的W應(yīng)使代價函數(shù)最小：

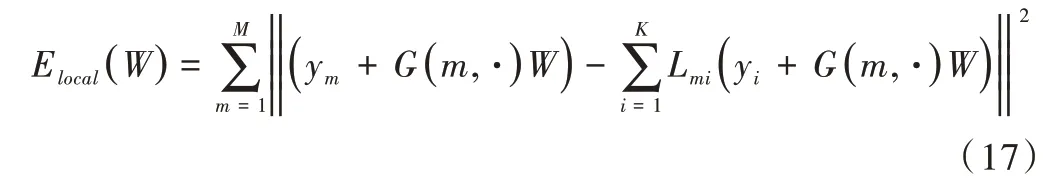
其中，G(m,?)表示G的第m行。

利用互補的全局和局部拓撲正則化項，在包含各種局部變形的復雜非剛體變換中保持局部結(jié)構(gòu)和全局連通性。

將點集配準問題視為基于高斯混合模型的正則化密度估計問題。根據(jù)目標函數(shù)的一般式以及給出的兩個保持全局局部拓撲的正則化項，目標函數(shù)可以改寫成：

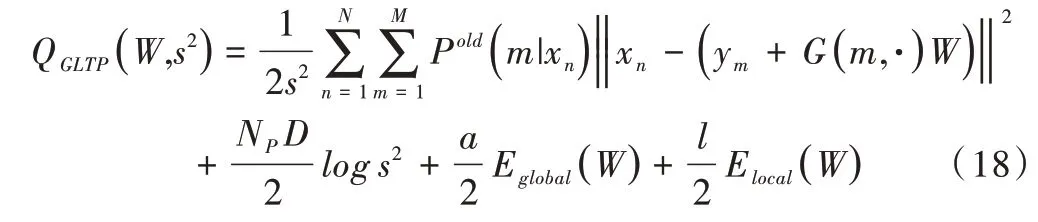
其中，α和λ是GMM 配準項和全局局部兩個拓撲項的權(quán)衡參數(shù)。

1.4 算法

給定X點集和Y點集，對它們進行聚類。先對聚類中心進行配準，找到聚類中心的對應(yīng)關(guān)系，并將對應(yīng)關(guān)系復制到點集的對應(yīng)關(guān)系中。在這一對應(yīng)關(guān)系的基礎(chǔ)上，更新Y點集的位置，使X點集和Y點集之間的初始狀態(tài)更為接近；再結(jié)合局部拓撲保持進行配準。算法流程如圖1 所示。

2 實驗結(jié)果與分析

分別對Chui-Rangarajan 合成數(shù)據(jù)集、斯坦福合成數(shù)據(jù)集、可變形的三維對象數(shù)據(jù)集和三維景觀人體數(shù)據(jù)集4 種數(shù)據(jù)進行以下實驗：①三維動物點集［17］；②三維頭部點集［18］；③三維人體點集［19］。然后，將實驗結(jié)果與現(xiàn)有先進的非剛性配準算法GLTP 進行比較和分析。所有實驗的軟件環(huán)境為MATLAB R2016a，硬件環(huán)境為16GB 內(nèi)存、AMD Ryzen 5 2600 六核處理器。

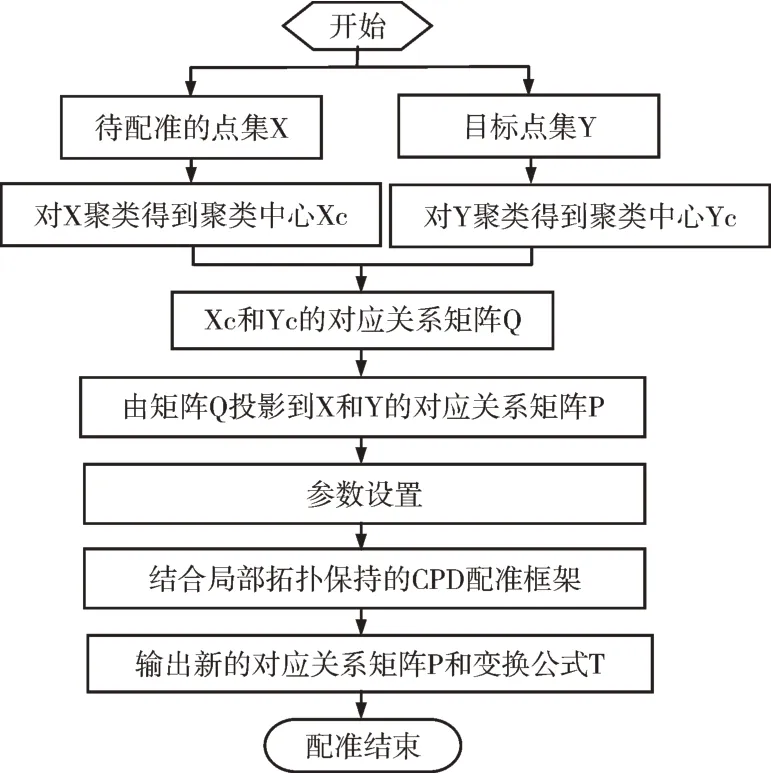
Fig.1 Algorithm flow圖1 算法流程

為展示配準過程，首先對大多數(shù)點集配準算法都采用Chui-Rangarajan 合成數(shù)據(jù)中的魚數(shù)據(jù)集進行實驗。其中，該點集形狀模型的模板點集和目標點集的點數(shù)相同。首先，分別對模板點集X 和目標點集Y 進行聚類，得到X 點集的簇a 和Y 點集的簇b，對每個簇的聚類中心進行配準。之后將聚類中心的對應(yīng)關(guān)系復制到點集之間的對應(yīng)關(guān)系，最后對點集的對應(yīng)關(guān)系進一步配準并完成配準。配準過程如圖2 所示（彩圖掃OSID 碼可見，下同）。

2.1 3D 動物點集

首先在3D 動物數(shù)據(jù)集上測試本文算法，該數(shù)據(jù)集中的點集提取自3D 網(wǎng)格模型。數(shù)據(jù)集中包含數(shù)個動物模型：獅子，包含5 000 個點；貓，包含7 207 個點；馬，包含8 431 個點，等等，且每個形狀模型的模板點集和目標點集的點數(shù)都相同。以貓模型和獅子模型為例對其進行實驗。圖3 和圖4 顯示兩種模型在不同變形程度下本文算法的配準結(jié)果。對于兩個不同形變的數(shù)據(jù)集，本文算法都提供了良好的配準結(jié)果，尤其是在高度可變性的四肢和尾巴部分。

采用歐式距離作為配準誤差［20］來評價配準算法性能。表1 顯示圖3 中貓模型在3 種不同形變下GLTP 和本文算法的配準誤差對比，表2 顯示圖4 中貓模型在3 種不同形變下GLTP 和本文算法的配準誤差對比，結(jié)果表明本文算法更具優(yōu)勢。

Fig.2 Diagram of registration process圖2 配準過程

Fig.3 Registration results of different deformable data sets of cat model圖3 貓模型不同形變數(shù)據(jù)集配準結(jié)果

Fig.4 Registration results of different deformable data sets of lion model圖4 獅子模型不同形變數(shù)據(jù)集配準結(jié)果

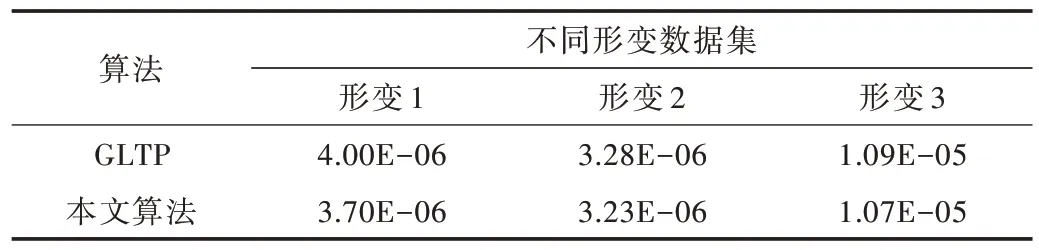
Table 1 Comparison of registration errors of cat model with different deformations at 7 207 points表1 7 207 個點的貓模型不同形變數(shù)據(jù)集配準誤差對比

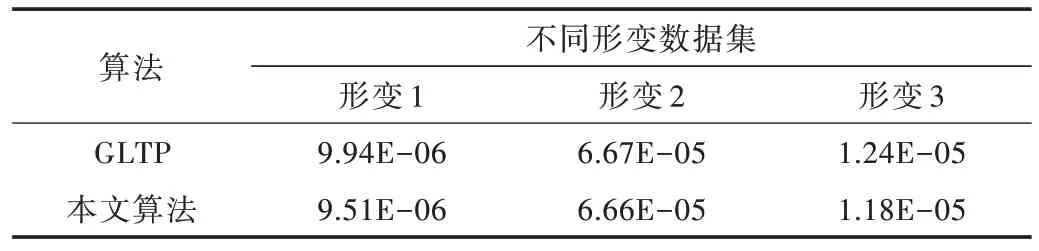
Table 2 Comparison of registration errors of different deformable datasets of lion model with 5 000 points表2 5 000 個點的獅子模型不同形變數(shù)據(jù)集配準誤差對比

除此之外，對本文算法在匹配不完整形狀（丟失部分數(shù)據(jù)）和具有離群值的情況下進行性能評估。圖5 為刪除了貓模型中尾巴上的部分點，以及在數(shù)據(jù)集中隨機添加一些異常值的配準結(jié)果，顯示在具有異常值的情況下本文算法仍具有較好的配準結(jié)果。

2.2 3D 頭部點集

分別在動物頭部數(shù)據(jù)集和人體頭部數(shù)據(jù)集上進行實驗。數(shù)據(jù)集來自斯坦福合成數(shù)據(jù)集，其中猴子頭部數(shù)據(jù)集的目標點集和模板點集數(shù)相同，均為7 958 個點。圖6 顯示3D 猴子頭部數(shù)據(jù)集在本文算法中的配準結(jié)果。

圖6 中猴子頭部模型展示了良好的配準結(jié)果，其中在GLTP 算法中的配準誤差是5.55E-05，本文算法中的配準誤差是5.51E-05，結(jié)果表明本文算法更具優(yōu)勢。

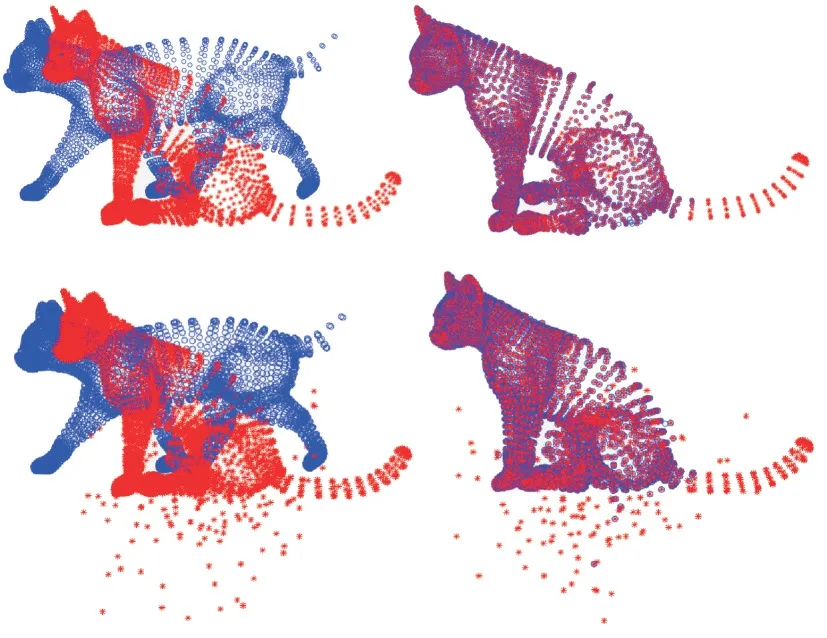
Fig.5 Registration results of point set of cat model with outliers圖5 具有異常值的貓模型點集配準結(jié)果

Fig.6 Registration results of 3D monkey head dataset圖6 3D 猴子頭部數(shù)據(jù)集配準結(jié)果

人體頭部數(shù)據(jù)集的目標點集和模板點集數(shù)相同，均為15 941 個點，配準結(jié)果如圖7 所示，頭部數(shù)據(jù)集包含細微的臉部表情，對配準算法有更高要求，結(jié)果表明對于頭部以及臉部的點集本文算法也有較好的配準結(jié)果。

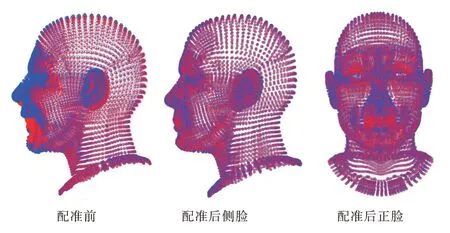
Fig.7 Registration results of 3D head model圖7 3D 頭部模型配準結(jié)果

2.3 3D 人體點集

最后在更具有挑戰(zhàn)性的3D 人體數(shù)據(jù)集上進行實驗，其中目標點集數(shù)為12 500，模板點集數(shù)為2 150，模板點集由人工標記，與目標點集相比具有顯著的形狀和位姿差異。圖8 顯示了3D 人體數(shù)據(jù)集在不同變形程度下本文算法的配準結(jié)果。如圖8 所示，對于兩個不同形變的人體數(shù)據(jù)集，本文算法都提供了良好的配準結(jié)果。

表3 顯示了圖8 中人體模型在不同形變下GLTP 和本文算法的配準誤差對比結(jié)果，結(jié)果表明本文算法更具優(yōu)勢。

Fig.8 Human body data set registration results圖8 人體數(shù)據(jù)集配準結(jié)果

Table 3 Comparison of registration errors of different deformation data sets of human model表3 人體模型不同形變數(shù)據(jù)集配準誤差對比

3 結(jié)語

在一致性點漂移（CPD）算法作為配準框架基礎(chǔ)上，本文提出了一種新的基于聚類的概率配準算法。該算法能夠處理各種二維、三維數(shù)據(jù)集配準問題。將聚類作為配準的初始化，將投影思想結(jié)合到CPD 中，同時引用全局局部拓撲，從而提高了配準算法的配準精度。在不同的二維和三維公共數(shù)據(jù)集上的非剛性點集配準實驗表明，該算法都具有較好的配準結(jié)果，優(yōu)于現(xiàn)有先進算法。后續(xù)將在人體姿態(tài)估計、三維運動估計等領(lǐng)域應(yīng)用此算法。