基于時變C-Vine-Copula 的風(fēng)險價值度量

文/虞情 李晉枝（中央民族大學(xué)）

一、引言

金融風(fēng)險的本質(zhì)是損失的不確定性，現(xiàn)代金融管理中這種不確定性并不是孤立的，需要考慮多變量之間的關(guān)系，多變量之間可能會因此存在著傳染效應(yīng)。經(jīng)濟資本的測算依據(jù)和核心技術(shù)在于風(fēng)險計量，從數(shù)據(jù)過濾到金融建模再到數(shù)據(jù)仿真，以及風(fēng)險測算和回溯檢驗，概括了經(jīng)濟資本風(fēng)險計量的整個過程。

VaR 是現(xiàn)代金融風(fēng)險計量常用的指標，本文以VaR 開展風(fēng)險研究。為了度量多元變量之間的非線性相關(guān)關(guān)系，本文借助時變C 藤Copula的方法。Copula 函數(shù)經(jīng)歷了從二元到多元，靜態(tài)到動態(tài)，傳統(tǒng)多元到藤結(jié)構(gòu)的研究階段，現(xiàn)在已經(jīng)比較成熟，也有許多經(jīng)典的文獻可以查閱借鑒。Copula 由Sklar（1959）引入并提出了Sklar 定理；Embrechts et al.(2003)用Copula 函數(shù)計算資產(chǎn)組合的VaR 值；Patton(2001)首先研究時變Copula 函數(shù)，令時變參數(shù)服從類似于ARMA 過程；Creal（2008）憑借GAS 模型將動態(tài)Copula 函數(shù)的建模應(yīng)用在函數(shù)種類上拓展到了阿基米德函數(shù)的動態(tài)模型；Bedford and Cooke（2001，2002）對二維情形開展研究，分別設(shè)定Pair-Copula，從而簡化了估計方法。近年來，全球經(jīng)濟的不確定性以及股票和債券市場的高度波動，刺激了投資者將黃金和其他貴金屬納入投資組合的興趣。貴金屬是一種有用的對沖工具，因為它們對其他金融資產(chǎn)的依賴性較低，當金融市場出現(xiàn)極端的市場波動時，貴金屬可能會表現(xiàn)出避險資產(chǎn)的特征。因此，本文以金、銀等六種貴金屬為研究對象，以基于GAS（1,1）理論的C-Vine-Copula 為研究方法，用蒙特卡洛模擬法計算這六種貴金屬資產(chǎn)組合的VaR。

二、研究方法

（一）C-Vine-Copula 模型

考慮一個n維隨機向量帶有聯(lián)合密度函數(shù)和分布函數(shù)F(x1,x2,…,xn)，根據(jù)Sklar（1959）定理，該隨機向量的聯(lián)合分布函數(shù)可以用Copula 函數(shù)表示為：

其中C(?)是Copula 函 數(shù)，F(xiàn)i(xi),i=1,…,n是隨機變量Xi的邊緣分布函數(shù)。當Fi(xi)都連續(xù)時，C(?)唯一確定。對于隨機向量X的聯(lián)合密度函數(shù)可以分解為條件函數(shù)形式：

在多元相關(guān)性中獲得更大建模靈活性的一種方法是進行Pair-Copula 分解，即將n元聯(lián)合密度函數(shù)分解為個二元Pair-Copula 密度函數(shù)與其邊緣密度的乘積，這種分解被稱為Vine Copula。因為Pair-Copula 的分解不唯一，為了使分解更加規(guī)范，Bedford &Cooke（2001,2002）引入了正則藤結(jié)構(gòu)，即R-Vine。該結(jié)構(gòu)包含節(jié)點以及連接節(jié)點的邊和樹結(jié)構(gòu)，每條邊就代表一個二元Pair-Copula 函數(shù)。常用的正則藤包括C 藤（C-Vine）和D 藤（D-Vine），本文基于C 藤進行研究。

定義1（C 藤）：當滿足以下條件時，則稱V為建立在n維變量的C藤結(jié)構(gòu)：

（1）V=(T1,… ,Tn?1)，Ti是構(gòu)成C 藤結(jié)構(gòu)的樹；

（2）第i棵樹的邊是第i+1棵樹的節(jié)點，且第i棵樹上擁有共同節(jié)點的兩條邊在第i+1棵樹上是相連的；

（3）第i（i=1,2,…,n?1）棵樹Ti有唯一的節(jié)點與n?i條邊相連，該節(jié)點稱為這棵樹的主節(jié)點，除主節(jié)點之外的其他節(jié)點僅連接一條邊。

C-Vine 結(jié)構(gòu)的n維聯(lián)合密度函數(shù)由下式給出：

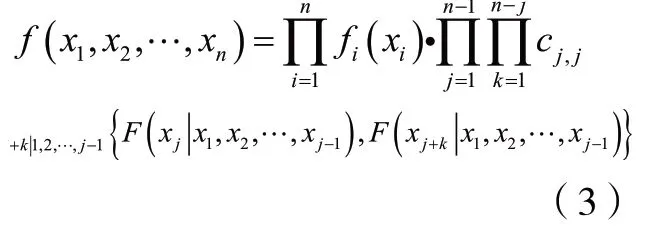
其中j代表第j棵樹，k代表第j棵樹中n?j條邊的遍歷。

（二）基于GAS 的二元時變Gaussian Copula

基于GAS 理論的Copula 時變參數(shù)的演化模式如下：

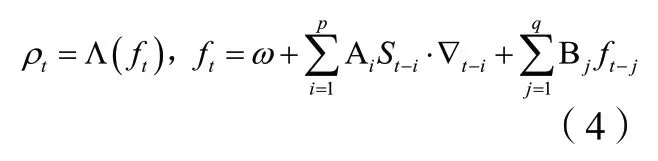
其中，ρt為Copula函數(shù)在t時刻的參數(shù)向量，Λ (?)為 修正的logistic 轉(zhuǎn)換函數(shù)對參數(shù)ft進行變換，ω、Ai(i=1,...,p)、Bj(j=1,...,q)為演化方程系數(shù)，令c(?)是Copula函數(shù)的密度函數(shù)，則為得分向量，是比例矩陣。令基于GAS(p,q)理論的時變二元正態(tài)Copula 函數(shù)的密度函數(shù)為：

（三）VaR 的計算

VaR 即風(fēng)險價值模型，對于一個投資組合的VaR，其定義為：

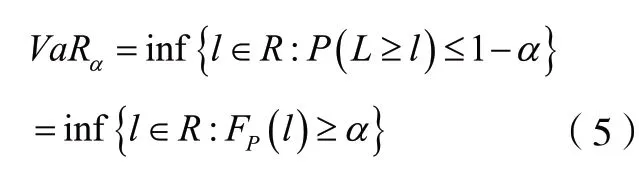
其中顯著性水平α∈(0,1)，投資組合的損失為L，即VaR 是使該投資組合的損失L超過l的概率不超過（1?α）的最小的l。若有n個投資對象，第i個投資對象在整個資產(chǎn)組合中所占的份額為iδ，那么整個投資的資產(chǎn)組合收益率為：

三、實證分析

本文選取六個比較具有代表性的貴金屬每日收盤價為研究對象，包括金、銀、鉛、鈀、銅、鎳，時間從2014 年6 月到2021 年3 月。計算其對數(shù)收益率序列：

（一）描述性分析

計算對數(shù)收益率序列的主要統(tǒng)計特征，得到表1。

由表1 可知，對于偏度來說，金和鉛呈右偏分布，其余四種貴金屬呈左偏分布；對于峰度而言，金、銀、鈀的收益率序列峰度高于3，具有厚尾特征。J-B 正態(tài)性檢驗的結(jié)果在顯著性水平0.05 下都拒絕服從正態(tài)分布的假設(shè)。接著對序列進行平穩(wěn)性檢驗和ARCH 效益檢驗顯示序列平穩(wěn)且具有ARCH 效應(yīng)，可以對邊緣分布擬合ARMA-GARCH模型。

表1 對數(shù)收益率時間序列統(tǒng)計特征

（二）擬合邊緣分布

根 據(jù)AIC 準 則，對ARMAGARCH 模型定階，找到最優(yōu)的ARMA-GARCH 模型如表2 所示。

表2 ARMA-GARCH模型參數(shù)估計結(jié)果

對模型得到的標準殘差序列進行ARCH 效應(yīng)檢驗和白噪聲檢驗，結(jié)果顯示殘差為白噪聲序列且不具有ARCH 效應(yīng)，可見擬合的模型可以較好地刻畫各貴金屬的對數(shù)收益率序列的邊緣分布。

（三）擬合時變C-Vine Copula

1.概率積分變換

對擬合邊緣分布得到的標準化殘差序列進行概率積分變換，K-S檢驗p 值都大于0.05，變換后的序列服從（0,1）上的均勻分布，可以擬合Copula 模型

2.主節(jié)點的確定

要擬合C-Vine-Copula，就得確定每棵樹的主節(jié)點，計算概率積分變換后序列間的相關(guān)系數(shù)，按相關(guān)系數(shù)從大到小排列，最大的即為主節(jié)點：從第二棵樹開始，計算條件概率序列的Kendall 秩相關(guān)系數(shù)，依次確定每棵樹的主節(jié)點，得到基于GAS（1,1）理論的C-Vine Gaussian Copula 的結(jié)構(gòu)及模型參數(shù)估計如表3。

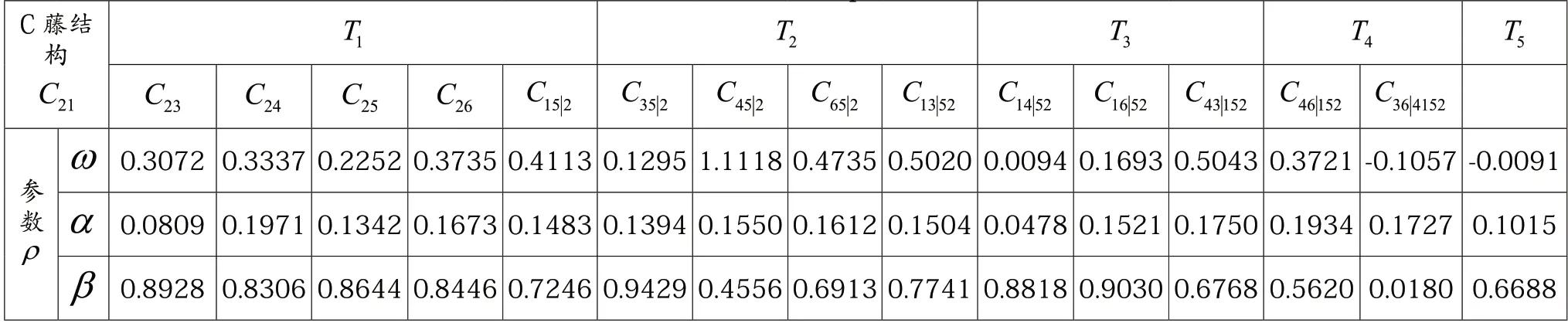
表3 基于GAS(1,1)的C-Vine-Copula 模型參數(shù)估計結(jié)果

4.VaR 的計算

下面通過蒙特卡洛模擬法計算六個貴金屬組合的VaR，先根據(jù)前面建立的C-Vine-Copula 模型擬合6個獨立同分布的序列，服從（0,1）均勻分布；再將這六個序列逆向推導(dǎo)出服從GAS（1,1）C-Vine Copula中Pair-Copula 分解的聯(lián)合分布函數(shù)的仿真序列，并通過概率積分變換將其轉(zhuǎn)換為模型的標準殘差序列；最后根據(jù)擬合的邊緣分布ARMAGARCH 模型將標準殘差序列轉(zhuǎn)化為收益率序列，并據(jù)此計算六個序列的組合收益率，重復(fù)計算1000 次，即可得到相應(yīng)顯著性水平下的VaR值（見表4）。

表4 GAS(1,1)C-Vine Copula模型的VaR似然比LR檢驗結(jié)果

由表4 可知，在10%和5%的顯著性水平下，檢驗p值顯示應(yīng)拒絕原假設(shè)；然而在1%的顯著性水平下，模型的失敗率0.75%接近期望值1%，檢驗p值顯示不拒絕原假設(shè)，說明基于GAS（1,1）C-Vine Copula 模型算出來的VaR 是有效的。

四、研究結(jié)論

本文基于GAS（1，1）理論建立C-Vine-Copula 模型，以六種貴金屬為研究對象，計算其資產(chǎn)組合的VaR。實證分析結(jié)果表明，精確度越高，該模型擬合效果越好，計算出來的VaR 越有效。