汽車銷量與新能源汽車關注度的格蘭杰關系研究及預測

文/賀享悅 路子彤（中國地質大學[北京]）

一、數據獲取與分析

（一）數據獲取

1.全國乘用車銷量

本文以月為單位，選取2017 年2 月-2021 年2 月間全國乘用車的實際銷售量，來研究大數據搜索趨勢與我國乘用車銷售量之間的關系。所采集數據來源于NE 時代網站。

2.搜索指數

本文使用的搜索指數以“新能源汽車”關鍵詞在搜索平臺的搜索量為數據基礎，計算關鍵詞的搜索頻次的加權和。由于搜索指數與全國乘用車銷售量的單位不同，可比性不強，所以本文通過Z-Score 標準化：，其中。

將數據轉化為無單位的Z-Score分值，使得數據標準統一化。

（二）相關性分析

本文通過使用斯皮爾曼相關系數對各平臺關于“新能源汽車”關鍵字的發展趨勢指數和全國乘用車銷售量進行相關性分析，定量評估兩者之間的關聯性。本文選取了“360搜索指數”和“搜狗指數”兩個指數與全國乘用車銷售量進行相關性分析。由表1 和表2 可知，360 關注趨勢指數與全國乘用車銷售量顯著相關；搜狗指數與之不存在相關性。因此，將針對360 搜索指數進行研究。

表1 “新能源汽車”關鍵詞搜索指數和全國乘用車銷售量的相關性檢驗

表2 單根檢驗結果

（三）季節性分解

本文選取了2017 年2 月-2021年2 月間全國乘用車實際銷售量和“新能源汽車”搜索指數進行研究，由于兩組數據都是以月度為時間序列數據，所以對數據進行季節性分解處理，使之更適用于長期趨勢的研究。

（四）ADF 單根檢驗

本文采用ADF 檢驗法來檢驗時間序列的平穩性。首先對時間序列進行對數化處理，再對時間序列進行單根檢驗。由表3、表4 可知，360 搜索指數時間序列與全國乘用車銷售量時間序列皆為1 階平穩，為同階平穩，符合協整檢驗的前提。

（五）協整檢驗及回歸方程

經ADF 單位根檢驗可知全國乘用車銷售量序列和“新能源汽車”360搜索指數序列雖自身非平穩，但是存在相似的趨勢和增長變化，因此兩者之間可能存在長期穩定的比例關系，并且兩者均為一節單證序列，可以進行協整檢驗。

協整檢驗采用EG 兩步法，首先對全國乘用車銷售量序列和“新能源汽車”360 搜索指數序列進OLS 回歸。設置“新能源汽車”360搜索指數為自變量ZHISHU，全國乘用車銷量為因變量XIAOLIANG，進行OLS 推導，協整回歸方程式如下：

其中ε 為殘差項。

對ε 殘差序列進行ADF 單位根檢驗，結果如表3 所示。

表3 對ε 殘差序列進行ADF 單位根檢驗

由此可知，殘差序列不存在單位根，表明該序列平穩。因此可以判斷全國乘用車銷售量和“新能源汽車”360 搜索指數之間存在長期均衡的協整關系。

（六）格蘭杰因果檢驗

因為兩組時間序列具有協整關系，所以本文使用格蘭杰因果檢驗模型來檢驗預測能力。

首先對var 模型的穩定性進行檢驗。如圖1 所示，點均落在單位圓內，對應的特征方程的特征根的絕對值小于1，模型穩定。

圖1 VAR穩定性檢驗

如表4，根據赤池信息量準則（AIC）、施瓦茨準則（SC）及漢南-奎因準則（HQ）結果選取了最佳滯后階段為2。

表4 確定VAR 模型滯后期

最后，進行格蘭杰因果檢驗。由表5 可知，在5%的顯著水平下，滯后二期的360 搜索指數是全國乘用車銷售量的格蘭杰原因。“新能源汽車”關鍵詞的360 搜索指數對全國乘用車銷售量的格蘭杰原因的概率為99.01%，因此關鍵詞“新能源汽車”的360 搜索指數可以作為一個有效的預測因子。

表5 格蘭杰因果分析結果

二、預測模型建立與分析

為了進一步驗證“新能源汽車”360 搜索指數對全國乘用車銷量的預測能力，本文先以全國乘用車銷量作為單一變量建立ARMA 模型，然后再加入搜索指數變量，建立多變量的VAR 模型，并對兩種模型的預測結果進行對比。模型都以2017 年3 月-2020 年2 月的數據為樣本期數據，2020 年3-9 月樣本期外的數據為驗證數據。

（一）ARMA 模型

通過觀察對數化后的全國乘用車銷量的自相關和偏自相關情況，本文建立并比較了幾個不同的模型，最終選擇擬合優度較高且AIC 與SC較小的ARMA(1,1）模型。得到預測結果如下：

銷量(t)=1221497.8816+AR(1)*銷量(t-1)+時間(t)+MA(1)*時間(t-1)

模型預測銷售量和實際銷售量的對比如圖2 所示。

由圖2 可以得出，該預測模型擬合程度相對較高。計算該預測模型的相關系數為0.89938145，擬合優度較高。

圖2 2020年3-9月全國乘用車實際銷量與基于ARMA模型的預測銷量的對比

（二）VAR 模型

構建VAR 模型要確定VAR 模型的滯后階段。本文通過比較，選擇滯后階數2 作為最佳滯后期建立VAR 模型。預測結果如下：

指數=0.862917095143* 指數(-1)-0.00323399781677* 銷量(-1)+8147.97046981

銷量=7.76447838425* 指數(-1)+0.303998512277* 銷量(-1)+1133702.05388

預測2020 年3-9 月全國乘用車汽車月度銷量數據對比，如圖3所示。

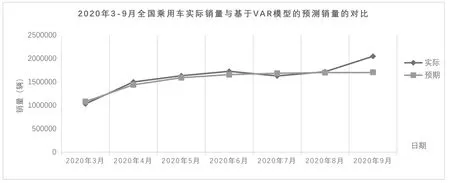
圖3 2020年3-9月全國乘用車實際銷量與基于VAR模型的預測銷售量的對比

由表4 可知，VAR 模型對全國乘用車月度銷量的平均預測誤差為2.8635625%，預測精度比較高，計算預測數據與實際數據的擬合優度相關系數為0.918020769，比ARMA預測模型的相關系數高，由此表明運用VAR 模型預測全國乘用車月度銷量的可行性和可靠性，具有更好的預測能力。

三、結論

“新能源汽車”360 搜索指數與全國乘用車銷售量存在正相關，且存在長期均衡關系，因此可以使用“新能源汽車”360 搜索指數預測全國乘用車銷售量。本文還選取了以“新能源汽車”作為關鍵詞的搜狗指數，經過相關性分析可知，“新能源汽車”搜狗指數與全國乘用車銷售量無相關性。說明盡管隨著互聯網的發展，各搜索指數反映網民關注趨勢，但其數據價值有所差異。

加入搜索指數的VAR 模型相較于傳統預測模型在樣本期間內和樣本期間外的預測精度均有較大提升。反映了“新能源汽車”360 搜索指數是一個有效的預測因子。該模型可以利用全國乘用車銷售量前2 月的實際銷售數據和搜索指數來預測一個月后對乘用車的需求，提高了預測的準確度和及時性，降低了對歷史數據量的要求。

由研究表明，人們對新能源汽車的關注對汽車市場的發展有著重要的影響，說明新能源汽車是當前汽車市場的重要發展方向，具有重要地位。