基于虛擬樣機的行星齒輪系統參數化建模及故障分析

劉奇洪 ， 賴展宇 ， 陶鴻景 ， 王 帥 ， 化一行

（中國礦業大學（北京）機電與信息工程學院，北京 100083）

0 引言

機械行業中使用最廣泛的傳動方式就是齒輪傳動。通過行星齒輪與定軸齒輪的對比，不難發現行星齒輪擁有多個優點，其中最顯著的就是在傳遞動力的時候能夠起到功率分流的作用，并且輸入軸和輸出軸在同一水平線上。因此，在實際機械應用當中，行星齒輪大量應用在復雜的大型機械裝備中，如風力發電、工程機械、直升機等。

但是，在現實中存在著很惡劣的工作環境，尤其是低轉速重載荷的情況，再加上機械系統中的行星齒輪由于制作過程中的誤差和裝配誤差而導致頻繁振動，因此，系統很容易出現裂紋、點蝕和脫落等局部故障。局部故障通常會逐步加劇，最終導致齒輪斷裂的情況發生。行星齒輪機構的齒輪一旦發生斷裂，會嚴重地影響整個機械系統的運轉并造成嚴重的財產損失，更重要的是機械機構的運行乃至工作人員人身安全都會受到威脅。

因此，國內外學者對行星齒輪系統動力學特性及故障診斷進行了大量研究，并且已經取得了豐富的成果[1-3]。而目前對行星減速輪系的建模分析大多都是建立在正常狀態下，缺乏對故障狀態下的行星輪系建模研究[4]。Ericson等考慮了行星輪軸承徑向和切向承載情況，計算了兩個方向上軸承剛度并引入模型中，研究行星齒輪傳動各階固有頻隨負載的變化[5]。Liang等在建立行星齒輪傳動系統動力學模型時，引入了嚙合間的相位差，分析了在太陽輪出現裂紋時的時變嚙合剛度[6]。Zhang等分別采用集中質量模型和有限元模型，對兩級行星齒輪傳動動態特性進行對比分析，研究了各剛度對系統振動模式的影響[7]。

隨著計算機仿真和虛擬樣機技術的發展，如今可通過建立齒輪傳動系統的虛擬樣機模型，對系統動力學響應特征進行分析[8]。因此，筆者在前人研究的基礎上，利用虛擬仿真對故障行星齒輪系統進行動力學特性分析，并進行了動力學仿真，希望為后續進行行星齒輪故障時的動力學分析和故障所需診斷提供可靠的理論支持。

1 含斷齒故障行星齒輪系統實體模型建立

1.1 建立故障行星齒輪系統各部件模型

本研究通過使用UG軟件開展對行星齒輪的建模工作，所具有基本參數如表1所示。

表1 基本參數表

1.2 齒輪的裝配

在UG中建模和裝配，本研究主要對太陽輪的斷齒在恒速恒載、恒速變載、變速恒載、變速變載的情況下發生故障的齒輪所具有的動力特性進行研究。

故障齒輪建模如圖1所示。

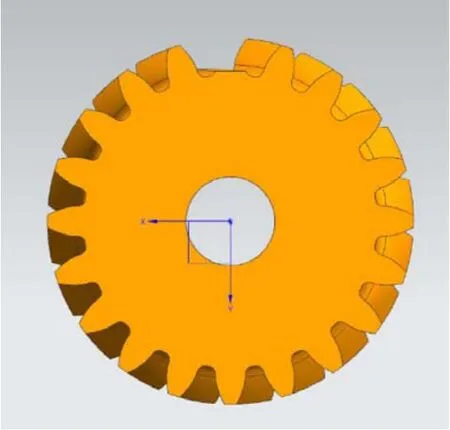
圖1 太陽輪斷齒

太陽輪斷齒后裝配圖，如圖2所示。

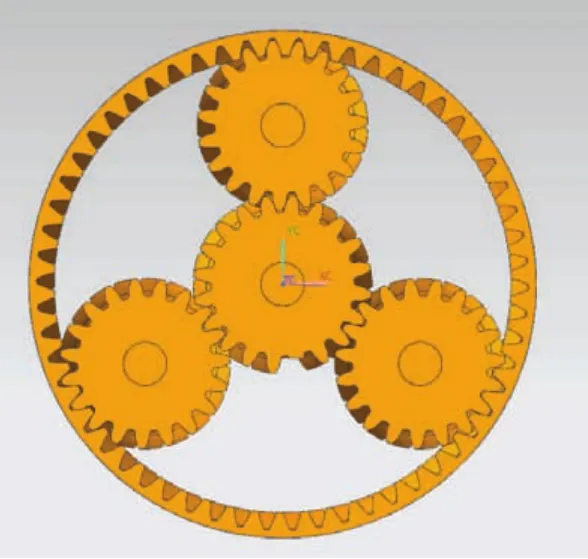
圖2 裝配圖

2 故障行星齒輪系統動力學分析

2.1 故障行星齒輪系統動力學模型的設置

將模型在UG中保存后導入到Adams中，設置太陽輪與地面轉動副，行星架與地面轉動副，行星輪與行星架轉動副，內齒圈與地面固定副，重力參數后得到如圖3所示的模型。

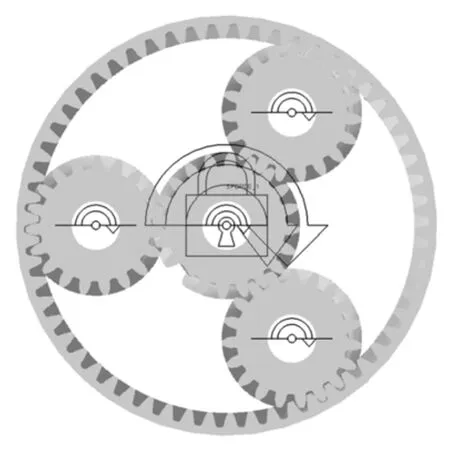
圖3 模型與旋轉副

2.2 參數計算

2.2.1 特征頻率的計算

轉速和齒數都會影響齒輪的嚙合頻率，在此系統中太陽輪、行星輪、齒圈的嚙合頻率均為

斷齒故障是齒輪嚴重故障種類之一，斷齒故障產生時，齒輪嚙合會在斷齒處產生沖擊振動。而在齒輪的旋轉中，按照一定的時間間隔會有規律地重復出現沖擊。而此時存在故障的行星輪需要和太陽輪、齒圈分別嚙合，如此就會導致在斷齒處有兩個不同的沖擊。此時行星輪的局部故障特征頻率為

經過計算得出行星齒輪系統的嚙合頻率：fm=61.96 Hz。

太陽輪局部故障特征頻率：fp=3.1 Hz。

2.2.2 接觸力的計算

實際上多由在齒頂處嚙合的輪齒分擔較多的載荷，為便于計算，通常按全部載荷作用于齒頂來計算齒根的彎曲強度。接觸力的計算公式如下：

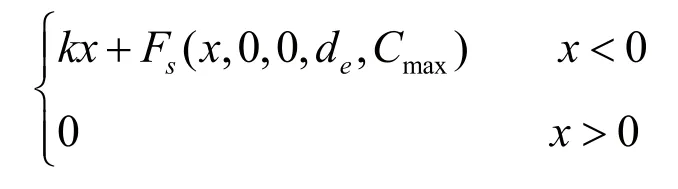
式中：k——嚙合剛度；

x——齒間距離；

e——非線性指數；

Fs——階躍函數；

Cmax——達到最大穿透深度時的最大阻力；

de——最大阻尼時的擊穿深度。

最終得出剛度如下。

3 仿真運動分析

3.1 仿真條件設置

由于采用MMKS單位制（以mm為長度單位），以下長度單位均使用mm。

1）添加行星輪與太陽輪的接觸：由接觸力計算結果得到剛度為力指數為1.5，阻尼為95 N·s/mm，穿透深度為0.1 mm。

2）添加行星輪與內齒圈的接觸：由接觸力計算結果得到剛度為力指數為1.5，阻尼為160 N·s/mm，穿透深度為0.1 mm。

3）添加負載力矩：為了使得在仿真過程中負載不發生突變，防止仿真數據異常，同樣選擇使用step函數，將負載力矩在0.2 s內由0增加至1.79×107N/m。

3.2 正常行星齒輪系統的仿真

正常行星齒輪系統中的太陽輪輸入轉速圖像如圖4所示，在0.2 s時加速到了1 500°/s，符合由step函數添加的轉速驅動。

圖4 太陽輪輸入轉速曲線

行星架的輸出轉速曲線如圖5所示，由理論計算所得行星架理論轉速應為384.6°/s，在仿真得到的曲線中，速度穩定后的行星架角速度均值約為384°/s，基本符合理論計算。

圖5 行星架輸出轉速曲線

在正常行星齒輪系統中，行星輪和太陽輪嚙合力幅值的時域和頻域曲線如圖6所示。

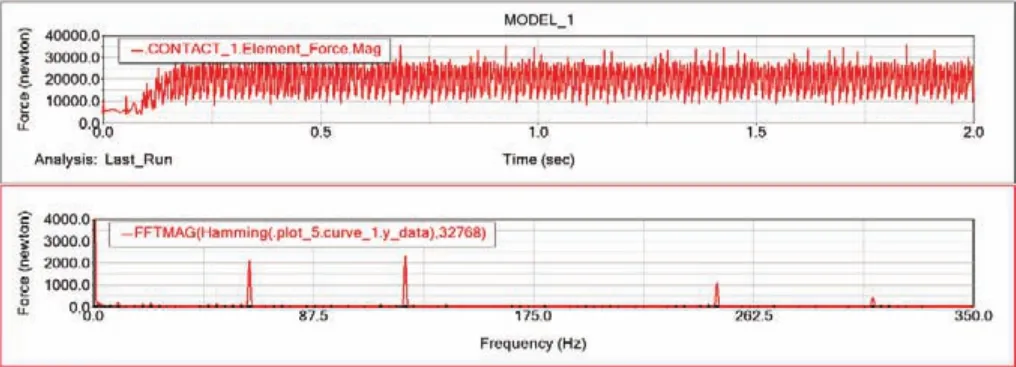
圖6 行星輪太陽輪嚙合力幅值的時域和頻域曲線

由嚙合力的時域曲線可知嚙合力的均值為21 816 N，其頻譜的峰值61.97 Hz及其倍頻成分，基本符合理論計算中行星輪系嚙合頻率（61.96 Hz）及其倍頻成分。

3.3 太陽輪單齒斷齒故障的行星齒輪系統仿真

3.3.1 恒速恒載時太陽輪單齒斷齒故障時的時域頻域分析

在恒速恒載情況下發生單齒斷齒故障時，太陽輪與行星輪嚙合力的時域頻域曲線如圖7所示。

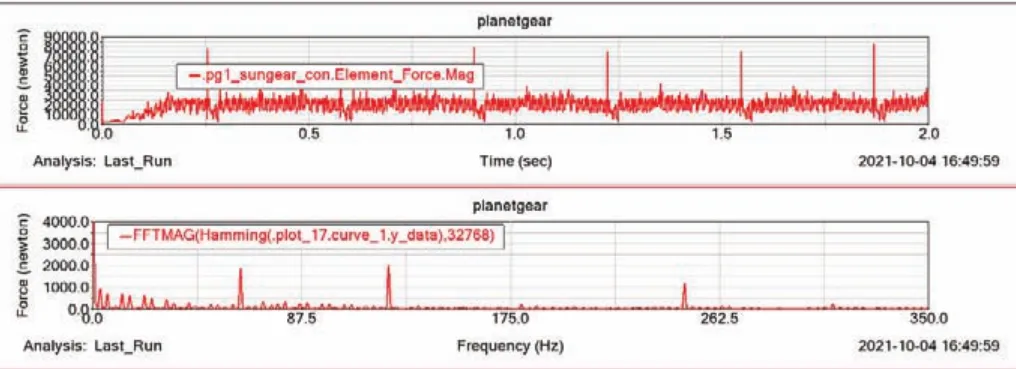
圖7 恒速恒載時太陽輪單齒故障的嚙合力時域頻域曲線

除去沖擊，其嚙合力均值為21 260 N，沖擊間隔為0.322 7 s，嚙合頻率前的邊帶成分第一個峰值出現在3.35 Hz處，大小為953.94 N；第二個峰值出現在6.1 s處，大小為733.84 N。此后的邊帶成分都以此規律分布，逐漸遞減。圖7中顯示出斷齒使得行星輪系運行過程中發生了強烈的沖擊，且在頻域曲線的低頻區域產生了較為明顯的邊帶成分。

3.3.2 恒速變載時太陽輪單齒斷齒故障時的時域頻域分析

在恒速變載情況下發生單齒斷齒故障時，太陽輪與行星輪嚙合力的時域頻域曲線如圖8所示。載荷以正弦周期變化，周期為4 s，峰值仍為1.79×107N/m。

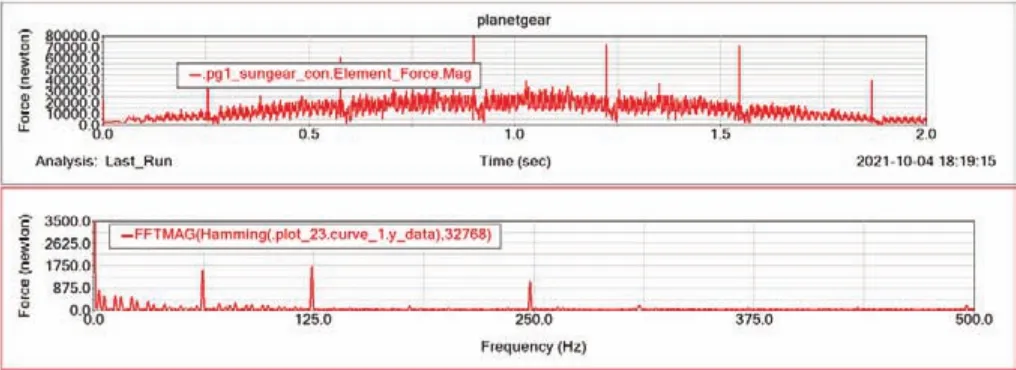
圖8 恒速變載時太陽輪單齒故障的嚙合力時域頻域曲線

圖中曲線顯示出在負載逐漸增加的過程中，斷齒帶來的沖擊強度越來越大，且在低頻區域會產生較為明顯的邊帶成分，邊帶成分頻率的分布規律與恒速恒載時相似。

3.3.3 變速恒載時太陽輪單齒斷齒故障時的時域頻域分析

在恒載、速度以正弦量變化的情況下發生單齒斷齒故障時，太陽輪與行星輪嚙合力的時域頻域曲線如圖9所示。其中，速度為正弦周期變化，周期為4 s，峰值仍為1 500°/s，其行星架速度響應曲線如圖10所示。

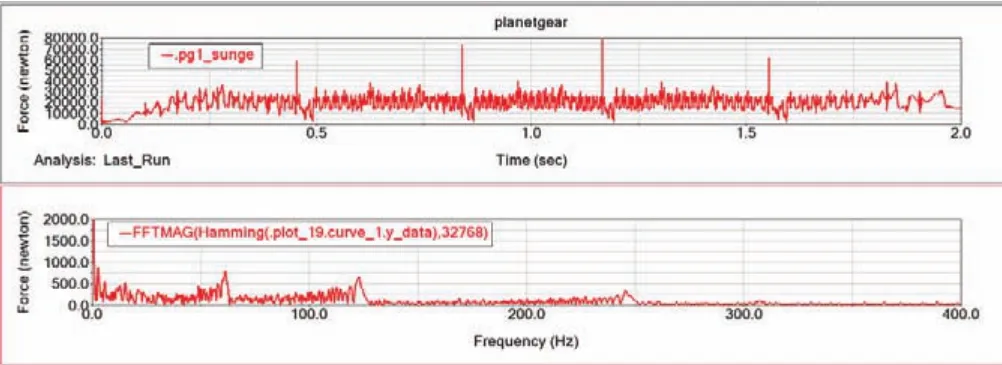
圖9 變速恒載時太陽輪單齒故障的嚙合力時域頻域曲線

圖10 行星架速度響應曲線

如圖所示，由于負載恒定，即使在低速區也產生了同樣大小的沖擊，但由于速度變化導致嚙合的峰值頻率在不斷變化，導致雖然能辨別出處于最大速度時的峰值頻率，但邊帶成分極為明顯。

3.3.4 變速變載時太陽輪單齒斷齒故障時的時域頻域分析

在變速變載情況下發生單齒斷齒故障時，太陽輪與行星輪嚙合力的時域頻域曲線如圖11所示。載荷以正弦周期變化，周期為4 s，峰值仍為1.79×107N/m；速度為正弦周期變化，周期為4 s，峰值仍為1 500°/s。

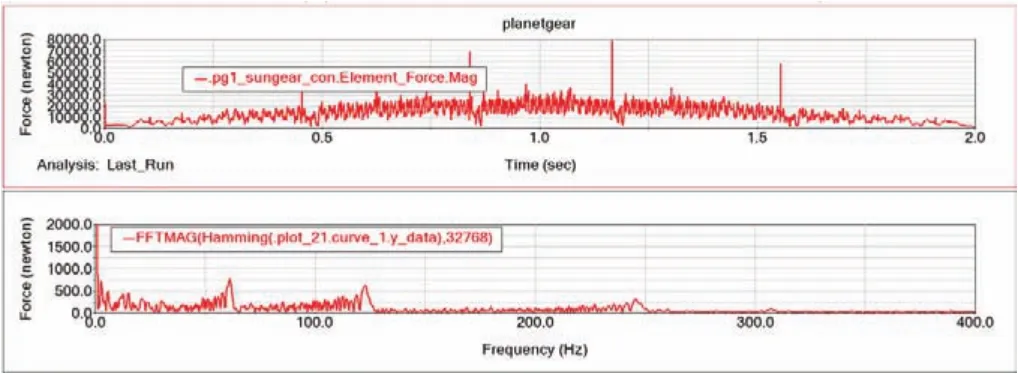
圖11 變速變載時太陽輪單齒故障的嚙合力時域頻域曲線

如圖11所示，沖擊隨著負載的增大而增大；同樣的，由于速度變化，嚙合力峰值頻率也在變化，導致邊帶成分極為明顯。

4 結語

1）本研究采用UG建模，基于ADAMS軟件對行星齒輪以及太陽齒輪斷齒故障進行了動力學仿真，通過采集齒輪的振動信號和頻譜特性，定位故障位置。

2）通過分析和對比正常行星輪系與故障行星輪系的嚙合力幅值與頻譜曲線得出，當齒輪發生斷齒故障時會導致嚙合力產生周期性沖擊，其嚙合力幅值與頻率曲線與正常情況偏離。且在變速變載等情況下，故障齒輪處于變速的情況下其嚙合力幅值頻率曲線的偏離程度最高。

3）根據以上結論，在分析故障行星輪減速系統時，可以通過分析其嚙合力幅值頻率曲線來判斷該系統是否存在特定的故障。