基于幾何代數(shù)理論的轉(zhuǎn)子堆疊裝配多目標(biāo)優(yōu)化

涂建波，李震，葛浩田，劉亮，劉洪慧

大連理工大學(xué) 機(jī)械工程學(xué)院，大連 116024

轉(zhuǎn)子是航空發(fā)動(dòng)機(jī)的重要部件，其裝配質(zhì)量對(duì)航空發(fā)動(dòng)機(jī)的整體性能有著重要影響，同心度和初始不平衡量是評(píng)價(jià)總裝質(zhì)量的重要參數(shù)[1]，轉(zhuǎn)子在高速旋轉(zhuǎn)運(yùn)動(dòng)時(shí)，初始不平衡量直接影響總裝的振動(dòng)特性。由于轉(zhuǎn)子無法避免在制造上的誤差，在多級(jí)轉(zhuǎn)子裝配過程中，其誤差不斷傳播和積累，最終可能使裝配后多級(jí)轉(zhuǎn)子的同心度和初始不平衡量超出工藝要求范圍，降低航空發(fā)動(dòng)機(jī)的可靠性和壽命。

轉(zhuǎn)子堆疊預(yù)測理論[2-4]在應(yīng)用上已經(jīng)有比較成熟的經(jīng)驗(yàn)，堆疊預(yù)測系統(tǒng)(Part measurement and Stacking Prediction system, PSP)是應(yīng)用于航空發(fā)動(dòng)機(jī)高壓壓氣機(jī)轉(zhuǎn)子裝配過程中的一種先進(jìn)的測量與預(yù)測裝配技術(shù)。在轉(zhuǎn)子裝配前, 針對(duì)轉(zhuǎn)子自身的測量數(shù)據(jù)，利用堆疊預(yù)測系統(tǒng)計(jì)算出最佳裝配方案，保證轉(zhuǎn)子裝配后同心度的最小化，在進(jìn)行大量裝配時(shí)，既可以提高轉(zhuǎn)子裝配質(zhì)量也顯著提高了裝配效率。隨機(jī)裝配時(shí)不考慮安裝相位對(duì)轉(zhuǎn)子精度的影響，即轉(zhuǎn)子不做任何安裝相位優(yōu)化直接對(duì)轉(zhuǎn)子進(jìn)行安裝。隨機(jī)裝配無法保證轉(zhuǎn)子整件同心度和初始不平衡量大小，容易令轉(zhuǎn)子質(zhì)心與回轉(zhuǎn)軸線的距離較大，使得轉(zhuǎn)子整體初始不平衡量非常大，加劇了整機(jī)的振動(dòng)，這是極其惡劣的一種情況。優(yōu)化裝配并非采用簡單的逐級(jí)最優(yōu)堆疊裝配方案，而是綜合考慮裝配后轉(zhuǎn)子整體狀態(tài)，合理調(diào)整各級(jí)轉(zhuǎn)子的安裝相位，令各級(jí)轉(zhuǎn)子質(zhì)心與回轉(zhuǎn)軸線的距離較小，使轉(zhuǎn)子整件的同心度和不平衡量達(dá)到最優(yōu)狀態(tài)，從而提高轉(zhuǎn)子的裝配質(zhì)量。隨機(jī)裝配和優(yōu)化裝配效果如圖1所示，其中C1、C2、C3為各級(jí)轉(zhuǎn)子質(zhì)心。

圖1 裝配示意圖Fig.1 Assembly schematic

在多級(jí)轉(zhuǎn)子裝配幾何誤差積累和傳播方面，目前已經(jīng)做了大量的研究。Yang等[5]提出了柱形零件裝配的誤差傳播和控制，闡述了多級(jí)轉(zhuǎn)子裝配時(shí)誤差的來源和傳播。Whitney等[6]建立了基于齊次矩陣變換的誤差表示方法，此方法不僅可以表示零件間的位姿關(guān)系，還可以表示裝配后部件的幾何誤差。Zhang等[7]提出了精密裝配時(shí)零件幾何誤差建模方法，該方法考慮了裝配結(jié)合面幾何誤差對(duì)裝配精度的影響。Mantripragada和Whitney[8]基于機(jī)械裝配中的狀態(tài)轉(zhuǎn)移模型提出了統(tǒng)計(jì)控制理論使裝配誤差最小化。在國內(nèi)，曹茂國[9]采用powell算法對(duì)轉(zhuǎn)子各級(jí)盤安裝邊進(jìn)行了工藝裝配優(yōu)化設(shè)計(jì)，減小作用在軸頸上的力和力矩。李立新等[10]提出基于遺傳算法的優(yōu)化理論提高了多級(jí)轉(zhuǎn)子安裝相位優(yōu)化的計(jì)算效率。琚奕鵬等[11]總結(jié)了多級(jí)轉(zhuǎn)子同心度、垂直度與不平衡量的疊加機(jī)理及裝配參數(shù)對(duì)不平衡量的影響關(guān)系。

由堆疊裝配的特點(diǎn)可知，總的裝配方案數(shù)目隨著轉(zhuǎn)子級(jí)數(shù)增加呈指數(shù)型增加，因此對(duì)計(jì)算效率要求較高。在多級(jí)轉(zhuǎn)子裝配建模方面，通常采用齊次矩陣變換。隨著幾何代數(shù)的發(fā)展，尤其是在李洪波[12]提出共形幾何代數(shù)之后，幾何代數(shù)得到了進(jìn)一步的完善和發(fā)展，幾何代數(shù)在機(jī)器人領(lǐng)域[13]、機(jī)構(gòu)運(yùn)動(dòng)學(xué)方面[14-15]的應(yīng)用越來越廣泛，采用幾何代數(shù)處理剛體的旋轉(zhuǎn)問題[16]與傳統(tǒng)方法相比具有一定優(yōu)勢(shì)，利用幾何代數(shù)進(jìn)行計(jì)算更加高效[17]。

本文基于幾何代數(shù)[18]理論建立各級(jí)轉(zhuǎn)子的誤差傳遞模型，取代傳統(tǒng)的齊次矩陣變換方法。綜合考慮轉(zhuǎn)子同心度和初始不平衡量，并基于遺傳算法對(duì)轉(zhuǎn)子進(jìn)行多目標(biāo)優(yōu)化，為航空發(fā)動(dòng)機(jī)裝配工藝設(shè)計(jì)提供指導(dǎo)。

1 基于幾何代數(shù)理論的誤差傳遞模型

1.1 幾何代數(shù)基本定義及運(yùn)算

設(shè){e1，e2，e3}是R3的自然基底，定義幾何積eiej為

并且運(yùn)算滿足分配律和結(jié)合律，三維空間幾何代數(shù)有23=8個(gè)基，其中正交基G={e1，e2，e3e1e2，e2e3，e2e3，e1e2e3=I}張成一個(gè)8維的線性空間。G1={e1e2,e2e3,e3e1}張成3維的子空間，其元素稱為雙重矢量(Bivector)，e1e2e3=I稱為偽標(biāo)量(Pesudoscalar)且eiI=Iei，eiejI=Ieiej，其中i，j=1,2,3。

在三維歐式空間中取2個(gè)普通矢量a、b；令a=a1e1+a2e2+a3e3，b=b1e1+b2e2+b3e3；a、b的幾何積ab為

式中：a·b表示矢量的內(nèi)積運(yùn)算；a∧b表示矢量的外積運(yùn)算。

三維空間中旋轉(zhuǎn)問題計(jì)算形式。例如：矢量a繞矢量b逆時(shí)針旋轉(zhuǎn)角度θ形成矢量a′。則

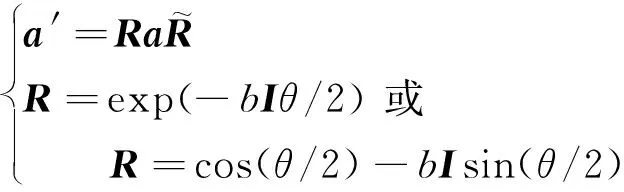
1.2 幾何代數(shù)和齊次矩陣計(jì)算效率對(duì)比

所以c為

由c的表達(dá)式可知旋轉(zhuǎn)算子轉(zhuǎn)化為指數(shù)相加的形式大大降低了運(yùn)算量。同理，基于齊次矩陣進(jìn)行旋轉(zhuǎn)變換時(shí)，令a=[ax,ay,az,0]T，b=[bx,by,bz,0]T，c=An…A2A1a；其中，Ai如式(1)所示。然而計(jì)算機(jī)計(jì)算An…A2A1時(shí)，為逐步相乘的計(jì)算形式，因此當(dāng)進(jìn)行大量的矢量旋轉(zhuǎn)操作時(shí)，齊次矩陣計(jì)算方法同幾何代數(shù)計(jì)算方法相比計(jì)算量大大增加。

令a=[1,1,1,0]T，b=[1/3,2/3,2/3,0]T，每次旋轉(zhuǎn)角度θi=π/2，當(dāng)n=100 000，150 000，200 000時(shí)，計(jì)算時(shí)間如表1所示。測試實(shí)驗(yàn)在3.4 GHz、 酷睿i5-7500處理器、8 G內(nèi)存的計(jì)算機(jī)平臺(tái)，由Python3.7編程完成。

(1)

如表1所示，隨著旋轉(zhuǎn)計(jì)算次數(shù)增加，2種計(jì)算方法所用時(shí)間均呈不斷增大的趨勢(shì)，但齊次矩陣計(jì)算方法用時(shí)較長，耗時(shí)增加幅度較大；幾何代數(shù)計(jì)算方法用時(shí)較短，且隨著計(jì)算次數(shù)的增加，耗時(shí)增加幅度較小。這是由于旋轉(zhuǎn)算子優(yōu)先進(jìn)行指數(shù)相加，相對(duì)于矩陣乘法運(yùn)算，計(jì)算量大大降低。因此，當(dāng)進(jìn)行大量旋轉(zhuǎn)運(yùn)算時(shí)，幾何代數(shù)計(jì)算方法更加高效。

表1 計(jì)算方法對(duì)比Table 1 Comparison of calculation methods

1.3 轉(zhuǎn)子堆疊誤差傳遞模型

1.3.1 基于幾何代數(shù)的坐標(biāo)系變換

取三維空間中的3個(gè)正交基向量{e1,e2,e3}表示一級(jí)轉(zhuǎn)子底面坐標(biāo)系的3個(gè)坐標(biāo)分量。記一級(jí)轉(zhuǎn)子下端面坐標(biāo)系{F1}={e1,e2,e3,0}，且圓心與坐標(biāo)原點(diǎn)重合。一級(jí)和二級(jí)轉(zhuǎn)子上下端面坐標(biāo)系變換如圖2所示。

令γx1、γy1、γz1為一級(jí)轉(zhuǎn)子上下端面的旋轉(zhuǎn)參數(shù)，R1為一級(jí)轉(zhuǎn)子上端面坐標(biāo)系相對(duì)于下端面坐標(biāo)系變化的旋轉(zhuǎn)算子，則一級(jí)轉(zhuǎn)子上端面和下端面坐標(biāo)系分別為

{F1}={ei,0}i=1, 2, 3

(2)

(3)

dx1、dy1為徑向誤差，dz1為高度誤差，則一級(jí)轉(zhuǎn)子上端面坐標(biāo)系位置矢量為

P1=dx1e1+dy1e2+(dz1+H1)e3

(4)

式中：H1為一級(jí)轉(zhuǎn)子的高度。

當(dāng)二級(jí)轉(zhuǎn)子安裝相位為θ1，一二級(jí)轉(zhuǎn)子配合面的旋轉(zhuǎn)算子為r1時(shí)，則二級(jí)轉(zhuǎn)子下端面坐標(biāo)系為

圖2 坐標(biāo)系變換示意圖Fig.2 Schematic diagram of coordinate system transformation

(5)

(6)

當(dāng)dx2、dy2為徑向誤差，dz2為高度誤差時(shí)，二級(jí)轉(zhuǎn)子上端面位置矢量為

(7)

以此類推，當(dāng)N級(jí)轉(zhuǎn)子裝配時(shí)，各級(jí)轉(zhuǎn)子上下端面坐標(biāo)系如式(8)和式(9)所示：

(8)

(9)

(10)

(11)

(12)

1.3.2 同心度和初始不平衡量計(jì)算方法

同心度定義為各級(jí)轉(zhuǎn)子端面圓心和參考軸線在同一平面上的重合程度，為方便衡量同心度的優(yōu)劣，利用各級(jí)轉(zhuǎn)子端面圓心到參考軸線的距離大小即不同心誤差來衡量轉(zhuǎn)子同心度優(yōu)劣水平。

轉(zhuǎn)子組件不同心誤差可以利用各級(jí)轉(zhuǎn)子上端面圓心位置矢量與基向量e3的外積值來計(jì)算，并取其最大值。當(dāng)多級(jí)轉(zhuǎn)子裝配時(shí)，由于轉(zhuǎn)子本身存在幾何誤差，隨著轉(zhuǎn)子組件數(shù)目增加，轉(zhuǎn)子組件不同心誤差不斷積累使得轉(zhuǎn)子組件的不同心誤差呈逐漸增大的趨勢(shì)，如圖3所示。

圖3 轉(zhuǎn)子組件不同心誤差Fig.3 Misalignment error of rotor assembly

裝配后k級(jí)轉(zhuǎn)子組件不同心誤差為

δk=max(P1∧e3,P2∧e3, …，Pk∧e3)

(13)

轉(zhuǎn)子整體不同心誤差為

δ=δN

(14)

轉(zhuǎn)子不平衡是由于轉(zhuǎn)子部件質(zhì)量偏心或轉(zhuǎn)子部件出現(xiàn)缺損造成的故障。不平衡的原因分為以下幾種：轉(zhuǎn)動(dòng)件本身形狀不對(duì)稱、加工制造上的公差、組裝安裝不當(dāng)、轉(zhuǎn)動(dòng)件運(yùn)轉(zhuǎn)時(shí)的變形、轉(zhuǎn)動(dòng)件破損磨耗和轉(zhuǎn)動(dòng)件附著異物等。不平衡量是轉(zhuǎn)子某平面上不平衡的量值大小。

只考慮各級(jí)轉(zhuǎn)子質(zhì)心相對(duì)于回轉(zhuǎn)軸線的偏移產(chǎn)生的不平衡，將各級(jí)轉(zhuǎn)子產(chǎn)生的不平衡矢量反映到軸徑兩平衡平面處的矢量和作為轉(zhuǎn)子整體的的初始不平衡量。如圖4所示，平面1、平面2、平面3表示各級(jí)轉(zhuǎn)子質(zhì)心所在平面，平衡平面A、B表示軸徑處初始不平衡量所在平面。最終取兩平衡平面處初始不平衡量的最大值作為轉(zhuǎn)子整體初始不平衡量大小。

由式(15)求得轉(zhuǎn)子回轉(zhuǎn)軸線，式(16)求得k級(jí)轉(zhuǎn)子質(zhì)心位置矢量向回轉(zhuǎn)軸線投影的長度。

L=PN

(15)

(16)

式中：μk為k級(jí)轉(zhuǎn)子質(zhì)心位置矢量投影到此轉(zhuǎn)子軸線時(shí)占軸線總長的比例系數(shù)。

第k級(jí)轉(zhuǎn)子不平衡矢量為

(17)

式中：mk為k級(jí)轉(zhuǎn)子質(zhì)量。

k級(jí)轉(zhuǎn)子不平衡矢量反映到平衡平面的初始不平衡量分量、k級(jí)轉(zhuǎn)子組件總的初始不平衡量和最終轉(zhuǎn)子整體的初始不平衡量的表達(dá)式分別為

(18)

(19)

u=uN

(20)

圖4 平衡平面處初始不平衡量Fig.4 Initial unbalance on balance plane

2 轉(zhuǎn)子堆疊多目標(biāo)優(yōu)化

采用多目標(biāo)優(yōu)化方法將轉(zhuǎn)子不同心誤差和初始不平衡量作為優(yōu)化目標(biāo)，求解不同心誤差和初始不平衡量的最優(yōu)組合。首先要確定偏差參數(shù)dxk、dyk、dzk、γxk、γyk、γzk；各級(jí)轉(zhuǎn)子簡化為柱形結(jié)構(gòu)[19]，取各級(jí)轉(zhuǎn)子高度Hk的上下偏差為±hk，直徑φk的上下偏差為±φk，如圖5所示，在公差范圍內(nèi)可得

|dxk|≤φk

(21)

|dyk|≤φk

(22)

|dzk|≤hk

(23)

(24)

(25)

(26)

(27)

圖5 零件尺寸模型Fig.5 Part size model

當(dāng)(hk-|dzk|)/0.5φk和(hk-|dyk|)/0.5φk非常小時(shí)，式(24)～式(26)改寫為

|γxk|≤(hk-|dzk|)/0.5φk

(28)

|γyk|≤(hk-|dzk|)/0.5φk

(29)

|γzk|≤(hk-|dyk|)/0.5φk

(30)

根據(jù)式(23)和式(28)，γxk和dzk被限制在圖6(a) 所示的陰影有區(qū)域內(nèi)。同理，由式(24) 和式(29)，γyk和dzk被限制在與γxk和dzk相同的陰影有界區(qū)域內(nèi)；由式(22)和式(30)，可以構(gòu)造出圖6(b) 所示的γzk和dyk的約束范圍；由式(21)～式(23)， 可以構(gòu)造出圖6(c)所示的dxk和dzk的約束范圍。如果首先確定dxk、dzk，剩余參數(shù)都會(huì)依據(jù)其約束范圍產(chǎn)生。規(guī)定所有零件的公差按照正態(tài)分布生成，任何超過[-3σ, +3σ]范圍的公差都舍棄。

圖6 偏差限制范圍Fig.6 Deviation limits

根據(jù)轉(zhuǎn)子工藝設(shè)計(jì)要求，確定直徑公差2φk和高度公差2hk，則可以確定dxk～N(0,φk/3)、dzk～N(0,hk/3)。dyk、γxk、γxk、γyk、γzk根據(jù)其約束范圍相繼求出，其中所有參數(shù)都服從正態(tài)分布。

各級(jí)轉(zhuǎn)子的安裝相位為θk，將θk代入式(11)求得安裝相位的旋轉(zhuǎn)算子rk；將γxk、γyk、γzk代入式(12)求得轉(zhuǎn)子上下端面變換的旋轉(zhuǎn)算子Rk；將dxk、dyk、dzk代入式(10)求得坐標(biāo)系位置矢量Pk；最后將Rk、rk、Pk代入式(8)和式(9)求出各級(jí)轉(zhuǎn)子坐標(biāo)系；通過式(13)和式(14)求出轉(zhuǎn)子不同心誤差；由式(18)和式(20)求出轉(zhuǎn)子整體初始不平衡量。

令函數(shù)f1為初始不平衡量，f2為不同心誤差；則

多目標(biāo)優(yōu)化數(shù)學(xué)模型為

(31)

式中：n為轉(zhuǎn)子安裝相位個(gè)數(shù)。

目前進(jìn)行優(yōu)化的算法很多，遺傳算法(Genet-ic Algorithm，GA)作為優(yōu)化算法，通過計(jì)算機(jī)模擬物種繁衍時(shí)，父代遺傳基因的重新組合和“優(yōu)勝劣汰”自然選擇機(jī)制的聯(lián)合作用，解決眾多復(fù)雜工程問題，因此利用遺傳算法求解多目標(biāo)問題在科學(xué)研究領(lǐng)域和工程實(shí)踐領(lǐng)域中得到了廣泛應(yīng)用[20]。采用其中最具代表性非支配排序遺傳算法II[21](Non dominated Sorting Genetic Algorithm II, NSGA-II)。其基本思想為：首先，隨機(jī)產(chǎn)生規(guī)模為D的初始種群，非支配排序后通過遺傳算法的選擇、交叉、變異3個(gè)基本操作得到第1代子代種群；其次，從第2代開始，將父代種群與子代種群合并，進(jìn)行快速非支配排序，同時(shí)對(duì)每個(gè)非支配層中的個(gè)體進(jìn)行擁擠度計(jì)算，根據(jù)非支配關(guān)系以及個(gè)體的擁擠度選取合適的個(gè)體組成新的父代種群；最后，通過遺傳算法的基本操作產(chǎn)生新的子代種群；依此類推，直到滿足程序結(jié)束的條件。其算法流程圖如圖7所示。

圖7 NSGA-Ⅱ算法流程圖Fig.7 Algorithm flow chart of NSGA-Ⅱ

3 4級(jí)轉(zhuǎn)子36安裝相位多目標(biāo)優(yōu)化算例

3.1 各級(jí)轉(zhuǎn)子參數(shù)

根據(jù)哈爾濱工業(yè)大學(xué)設(shè)計(jì)的HUE-SHS-06[22]模擬轉(zhuǎn)子的直徑和高度公差，計(jì)算一組轉(zhuǎn)子參數(shù)，如表2所示。模擬轉(zhuǎn)子止口配合為過盈配合，螺栓和螺栓孔為間隙配合，只考慮剛體堆疊效果，不考慮螺栓緊固后的受力變形。

表2 各級(jí)轉(zhuǎn)子參數(shù)Table 2 Rotor parameters of each stage

令所有參數(shù)符合正態(tài)分布，將表2中高度和直徑參數(shù)代入式(21)～式(24)確定平移參數(shù)dxk、dzk然后將其代入式(28)～式(30)，可以相繼求出旋轉(zhuǎn)參數(shù)γxk、γyk、γzk。平移參數(shù)精度超過小數(shù)點(diǎn)后4位對(duì)結(jié)果影響可以忽略不計(jì)，故取小數(shù)點(diǎn)后4位，同理，旋轉(zhuǎn)參數(shù)保留3位有效數(shù)字，取一組數(shù)據(jù)如表3和表4所示。

表3 平移參數(shù)數(shù)據(jù)Table 3 Translation parameter data

表4 旋轉(zhuǎn)參數(shù)數(shù)據(jù)Table 4 Rotation parameter data

3.2 優(yōu)化及分析

裝配過程中，各級(jí)轉(zhuǎn)子的具體形狀尺寸已經(jīng)確定，轉(zhuǎn)子間的安裝相位是唯一可控變量。轉(zhuǎn)子的安裝相位由螺栓孔分布決定，螺栓孔均勻分布，參數(shù)θk表示安裝相位。

轉(zhuǎn)子不同心誤差和初始不平衡量雙目標(biāo)優(yōu)化目標(biāo)函數(shù)及其約束為

(32)

NSGAⅡ算法參數(shù)選取如表5所示。優(yōu)化過程中記錄第5、10、20、100次迭代時(shí)的Pareto前沿點(diǎn)，取最后一次迭代記錄的Pareto前沿點(diǎn)作為最終優(yōu)化得到的Pareto最優(yōu)解集，如表6所示。多目標(biāo)優(yōu)化Pareto前沿收斂過程如圖8所示。取10組隨機(jī)裝配時(shí)初始不平衡量、不同心誤差和安裝相位如表7所示，優(yōu)化裝配和隨機(jī)裝配誤差對(duì)比如圖9所示。

表5 參數(shù)選取Table 5 Parameter selection

表6 優(yōu)化結(jié)果Table 6 Optimization results

表7 隨機(jī)裝配結(jié)果Table 7 Random assembly results

由圖8可以觀察出，目標(biāo)函數(shù)在優(yōu)化前20次迭代過程中收斂速度較快，有著較高的收斂效率。在20～100次迭代過程中，隨著迭代次數(shù)的增加，

目標(biāo)函數(shù)只進(jìn)行了略微收斂，收斂速度大幅度降低甚至保持不變意味著已經(jīng)達(dá)到最優(yōu)解集狀態(tài)，將此時(shí)獲得的解集作為最終優(yōu)化裝配方案。

由圖9可以觀察出優(yōu)化裝配結(jié)果集中分布在初始不平衡量和不同心誤差都比較小的區(qū)域，然而隨機(jī)裝配時(shí)誤差分布范圍較廣且初始不平衡量和不同心誤差較大。由于誤差較小的裝配方案數(shù)目非常少，隨機(jī)裝配時(shí)無法保證獲得較小誤差的裝配方案，從而容易造成裝配后轉(zhuǎn)子不合格情況。采用優(yōu)化裝配方案可以預(yù)測裝配后轉(zhuǎn)子誤差情況，既提高了裝配質(zhì)量也提高了裝配效率。

圖9 優(yōu)化裝配與隨機(jī)裝配對(duì)比Fig.9 Comparison of optimized assembly and random assembly

根據(jù)隨機(jī)裝配方案和優(yōu)化裝配方案數(shù)據(jù)，取不同心誤差和初始不平衡量平均值進(jìn)行對(duì)比，如表8所示。采用優(yōu)化裝配方案時(shí)，初始不平衡量降低97.88%，不同心誤差降低65.10%，大幅度提高了裝配質(zhì)量。

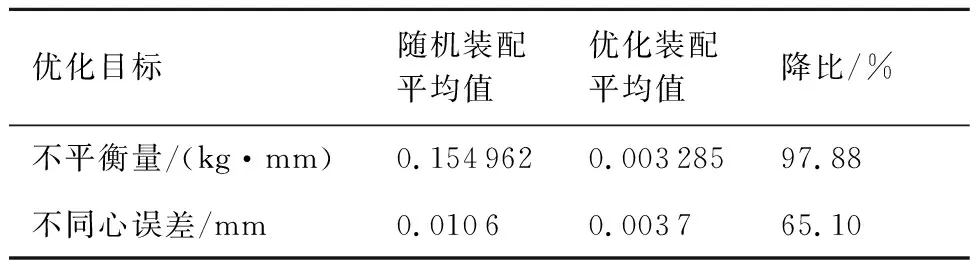
表8 初始不平衡量、不同心誤差降低百分比

優(yōu)化裝配和隨機(jī)裝配不同裝配組件數(shù)對(duì)應(yīng)的初始不平衡量和不同心誤差數(shù)據(jù)如表9～表12所示。取優(yōu)化裝配和隨機(jī)裝配轉(zhuǎn)子組件不同心誤差平均值進(jìn)行對(duì)比，如圖10所示；取優(yōu)化裝配和隨機(jī)裝配轉(zhuǎn)子組件初始不平衡量平均值進(jìn)行對(duì)比，如圖11所示。

表9 優(yōu)化裝配轉(zhuǎn)子組件初始不平衡量

表10 優(yōu)化裝配轉(zhuǎn)子組件不同心誤差

表11 隨機(jī)裝配轉(zhuǎn)子組件初始不平衡量

表12 隨機(jī)裝配轉(zhuǎn)子組件不同心誤差

圖10 轉(zhuǎn)子組件不同心誤差Fig.10 Concentricity of rotor subassembly

由圖10和圖11顯示，隨機(jī)裝配時(shí)，不同心誤差和初始不平衡量隨裝配組件數(shù)增加而不斷增大，且增幅較大。優(yōu)化裝配可以合理安排各級(jí)安裝相位，雖然隨裝配組件數(shù)目增加不同心誤差也不斷增大，但是增幅較小，且最終使不同心誤差穩(wěn)定在0.003 7 mm附近。初始不平衡量呈先增大后減小的趨勢(shì)，同隨機(jī)裝配相比大大降低了初始不平衡量。因此，相對(duì)于隨機(jī)裝配，優(yōu)化裝配降低了轉(zhuǎn)子整體的初始不平衡量和不同心誤差，提高了轉(zhuǎn)子裝配質(zhì)量。

4 結(jié) 論

1) 基于幾何代數(shù)理論建立航空發(fā)動(dòng)機(jī)多級(jí)轉(zhuǎn)子堆疊裝配誤差傳遞模型模，使模型更加簡潔高效，并定義了基于幾何代數(shù)理論求解不同心誤差和轉(zhuǎn)子軸頸處初始不平衡量的方法。

2) 利用遺傳算法對(duì)不同心誤差和初始不平衡量進(jìn)行多目標(biāo)優(yōu)化，確定各級(jí)轉(zhuǎn)子的最優(yōu)安裝相位角，得到一組Pareto最優(yōu)解集作為最優(yōu)裝配方案。優(yōu)化的裝配方案可以預(yù)測轉(zhuǎn)子不同心誤差和初始不平衡量，與隨機(jī)裝配方案相比初始不平衡量降低97.88%，不同心誤差降低64.81%，提高了裝配質(zhì)量。

3) 基于幾何代數(shù)理論的計(jì)算方法應(yīng)用于轉(zhuǎn)子裝配領(lǐng)域，雖然在處理大量旋轉(zhuǎn)問題時(shí)計(jì)算效率較高，但在計(jì)算機(jī)編程應(yīng)用方面，基于幾何代數(shù)開發(fā)的應(yīng)用程序較少。因此實(shí)際應(yīng)用時(shí)，幾何代數(shù)方法具有一定難度，而基于齊次矩陣變換更加方便和易于實(shí)現(xiàn)。在多目標(biāo)優(yōu)化方面，優(yōu)化對(duì)象為剛體模型沒有考慮止口配合面的受力變形，這方面有待進(jìn)一步研究。