目標電磁仿真結果可信度的驗證方法對比分析?

劉文鵬 宋 廣

（91404部隊 秦皇島 066001）

1 引言

隨著現代技術的發展，對復雜目標電磁散射和輻射特性的研究變得越來越重要，很多國防和民用領域都涉及到復雜目標的電磁建模問題，如雷達系統的設計與目標識別、軍用武器的隱身與反隱身、復雜環境的電磁兼容問題等［1～2］。如果對這些目標進行實體建模，單純依靠模型實驗的方法獲得目標的電磁特性，一方面代價高昂，另一方面實際測量易受各種因素影響，測量結果往往存在較大誤差，而采用計算機進行精確電磁仿真則要高效和經濟的多，其中仿真結果可信度的定量評估一直是該領域研究的重點［3～4］。作為電磁建模仿真有效性評估的核心內容，對仿真結果可信度進行驗證可以消除主觀目測評估的不確定性和不穩定性，為仿真模型的修正及改進提供指導。

目前主要的仿真結果驗證方法是將相同條件下的模型計算結果與標準驗模數據進行比對，通過比對數據差異并分析差異原因來評價仿真結果的可信度，標準的驗模數據包括解析解、其他經過驗證的模型軟件計算結果以及實驗測量數據等［5］。其中，解析解具有閉合形式的解，因此可用于精確判斷被校驗模型的置信度，但是該方法通常只能用于一些特殊計算條件；此外，建模人員往往也會從多種渠道獲得一些具有較高置信度的模型計算數據，將相同限定條件作為計算參數輸入待驗證模型，將仿真結果與驗模數據進行比對，得到模型在限定條件下的可信度；而實驗驗證是確定建模軟件能否最終被用戶接受不可或缺的一環，通過實驗驗證可以評估模型數據的誤差，并且能夠分析和定位誤差的來源。因此，使用測量或實驗數據與模型仿真結果進行比對，是公認的具有較強說服力的驗模方法。

2 常用數據比對方法

可見，模型驗證離不開不同數據集之間的比對，因此如何科學地比對多組數據，對于模型驗證非常重要。以往數據比對主要依靠研究人員閱讀分析以判斷它們的相近程度，這種方法帶有明顯的局限性和主觀性，且沒有確定的比較基準，而利用理論方法進行數據比對可以在一定程度上解決這些問題，下面是幾種常見的電磁模型數據比對方法［6］。

2.1 點對點比較法

在低頻區或諧振區，復雜目標的電磁散射場隨姿態角的變化通常是比較緩慢的，因此可采用點對點比較法，利用測量數據對模型仿真數據進行校驗。以RCS數據為例，具體方法為取每一個相同角度的RCS理論值與測量值（單位dB·sm，下同）之差，對所有角度上的差值平方求和再平均，經開方后得到理論數據與測量數據之間的誤差ε1：

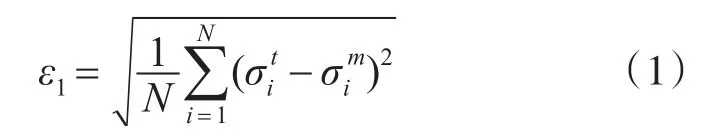
其中，i=1,2,…,N為數據序號；N為數據總量。根據ε1的大小可以評估模型的精度，ε1越小表明理論值與測量值吻合的越好，模型精度也越高。

2.2 平滑比較法

在高頻區，復雜目標的電磁散射場是由大量散射中心的散射場矢量疊加合成的，合成后的散射場幅度和相位隨姿態角的變化非常劇烈，散射場的數據具有復雜的起伏性質，因此采用平滑比較法更有效。具體方法為針對模型和測量得到的RCS數據，選擇適當的滑動窗口寬度和滑動步長，通過滑動窗口在每個窗口內取數據的平均值，從而獲得新的理論數據序列或測量數據序列，誤差ε2為

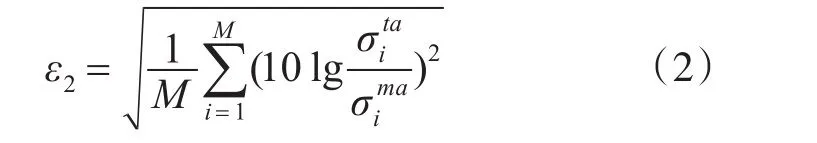
其中，i=1,2,…,M為數據序號；M為平滑后的數據總量。滑動窗口寬度的選取一般由兩個因素決定：一是目標姿態相對雷達視線變化的快慢及變化范圍，二是目標散射本身的起伏快慢。因為這兩個因素本身的不確定性，窗口寬度一般取為1°～5°。滑動步長的最小值是數據采集的角度間隔，最大值是窗口寬度，一般滑動步長取為1°～3°較為合理。

2.3 加權比較法

7）計算ADM、FDM和GDM的算術平均值和信任度直方圖。以ADM為例，其值可以劃分為6個區間，每個區間可以用自然語言來描述。與概率密度函數類似，信任度直方圖給出了數據在各個區間的分布情況，告訴研究者需要將注意力集中于哪些區間。根據表3記錄各區間中ADM值的數量，然后計算比例即可得到直方圖。

1）選定能夠描述典型散射特征的多種目標作為電磁散射仿真模型的評估標準體，表1給出了幾種重要散射特征及其對應的標準體。

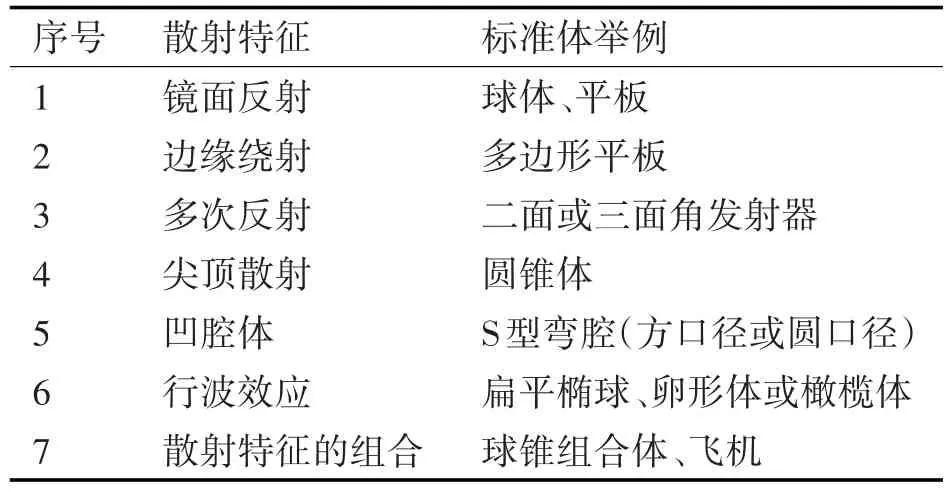
表1 典型散射特征的標準體舉例

FSV的具體實現過程如下［9～12］。

3）根據需要，選取用于評估的目標特征量（如RCS、角閃爍、一維距離像等），定義如下模型：

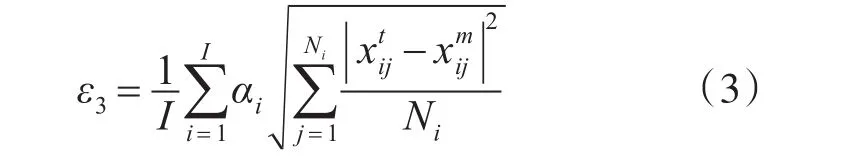
其中，I為標準體個數；為第i個標準體的第j個理論評估量；為第i個標準體的第j個測量評估量；Ni為第i個標準體的評估量數據總數；αi為第i個標準體分配的目標權，所有目標權數值和為1；ε3為模型吻合度。

顯然，要合理地實現該方法，關鍵有三點：1）標準體的選擇；2）目標特征量的選擇；3）加權系數αi的分配。上述三點中，最重要的是第三點加權系數的分配，目前主要依靠物理概念和實際試驗來確定，因此加權比較法在實際中很難應用。

3 特征選擇驗證

特征選擇驗證（Feature Selective Validation，FSV）作為電磁仿真有效性評估體系的核心方法，其基本思路是從原始數據中提取兩類信息，即幅度特征和要素特征，前者體現數據的整體變化，后者描述數據向上或向下的尖峰，通過這兩類信息，FSV可以得到不同層次（整體、局部、逐點等）的驗證結果［7］。

3.1 核心思想

FSV方法由圖1中的六分等級量表發展而來，其核心目的是盡量剔除數據比較過程中的“個人差異”，表中每個節點及其結果都只需使用二元判定，從而使整個比較過程都是六分制量化，數量描述符也被分配到這些值上，這樣有助于提高個人技能，也有助于知識共享類別的開發［8］。

圖1 FSV的六分等級量表

3.2 具體實現

2）根據標準體在驗模評估中的地位，尤其是在表征待研究目標特征量中的重要性以及預測的難易程度，給每一個標準體分配相應的權值，稱為目標權，權值按0～1選取，越重要的權值越大。

20世紀中國思想界，既有以意欲為根基的時間觀(梁漱溟)，也有以情感為時間奠基的唯情主義時間觀(朱謙之)，更有以“道”為根基的絕對時間觀(金岳霖)和以心-本體為根基的時間觀(熊十力、牟宗三)。凡此種種，充滿意趣，給人以無窮的遐想與安慰，但終究可愛而不可信。圍繞現代中國與現代中國文化的重建，胡適以科學理性為根基理解時間，不僅可信，而且賦予過去、現在、未來以情感態度與價值，使冷冰冰的物理時間有了溫度、多了可愛。這是胡適時間觀的最大特點，也是他留給現代中國哲學的重要財富。

1）讀取原始數據，獲取FSV比較操作的重疊抽樣窗口。如果兩組數據的抽樣點不同，則必須至少對其中一組數據進行插值或者重采樣；同時，對兩組數據補零到數據長度為2k以滿足使用快速Fouri?er變換。

樣品測定值的穩定性通過每次樣品序列前和序列中穿插咖啡因標準品測定來評估，每次至少測定6平行。標準值δ13C=-27.771‰與δ15N=1‰，測定值與標準值必須SD＜0.3‰，否則系統穩定性差影響檢測結果的準確性，需重新檢查儀器系統。

產后出血指的是胎兒娩出后24小時內出血量大于500 ml,是產婦分娩期的嚴重的并發癥,同時也是造成產婦死亡的主要原因,位居我國產婦死亡原因首位,發生率約為2%~3%,多數為發生在產后2小時以內的產后出血達80%以上[1]。本文選取2015年3月~2016年3月之間收集的30例產后出血病例,對其臨床護理觀察分析如下。

（1）對變換后數據集的前4個數據點進行Fou?rier逆變換，得到直流分量DC1(n)和DC2(n)，n為數據位置。忽略變換后數據集的前四個點以過濾直流分量，對兩組數據第5～N個數據點分別求和，得到剩余數據的總和S，N為數據集中的數據總數。

2）獲取原始數據的低頻分量。

（2）選取40%累計點。從變換后數據集的第5個點開始累加其后各點的值，直至達到數據總和S的40%時停止累加，并選擇該點為40%累計點i40%：

（4）對濾波后的數據集做Fourier逆變換，得到原始空間的低頻數據，分別用Lo1(n)和Lo2(n)表示。

“以風險指數進行風險評價分段：評分≤5分為低風險，即可以接受的風險（L）； 6～15分為中等風險，不可接受的風險（M）；>15分為高風險，不可接受的風險（H）。在實際風險預防與應對中，重點針對6分以上的風險。”沈崇德補充道。

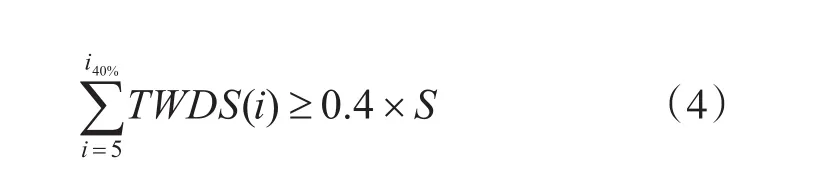
其中，i為數據集中的元素序號；TWDS（i）為變換后數據集中的第i個數據。在40%累計點i40%的基礎上加5就得到截斷點ibp。

（3）選取低通濾波窗口，如表2所示，過濾變換空間的數據。

表2 低通、高通濾波器對應值

where n is refractive index, which is related with λ. Therefore, the absorption coefficient, α, can be calculated from Eq. (4)[19],

3）獲取原始數據的高頻分量。其計算過程與低頻分量類似，只不過將低通濾波窗口改為高通濾波窗口（表2），然后進行Fourier逆變換，得到原始空間的高頻數據，分別用Hi1(n)和Hi2(n)表示。

土建施工是一個龐大的體系，需要對各個方面進行管理。管理人員要在工程開展前，分析研究圖紙的內容，對整個工程要有一個總體概念和認識，并對整體施工進行統籌安排。做到全面的思考問題，考慮各個因素可能造成的影響，同時做出合理有效的施工組織計劃。

教學內容分層是保證高中化學分層教學能夠順利實施的關鍵，只有在科學合理的化學教學內容分層下，化學分層教學模式才能夠發揮出應有的作用，提升學生的化學理解能力以及化學應用能力。因此，相關的高中化學教職人員必須要對化學教學內容進行準確的分層基礎。

4）逐點計算幅值差異量（ADM）：

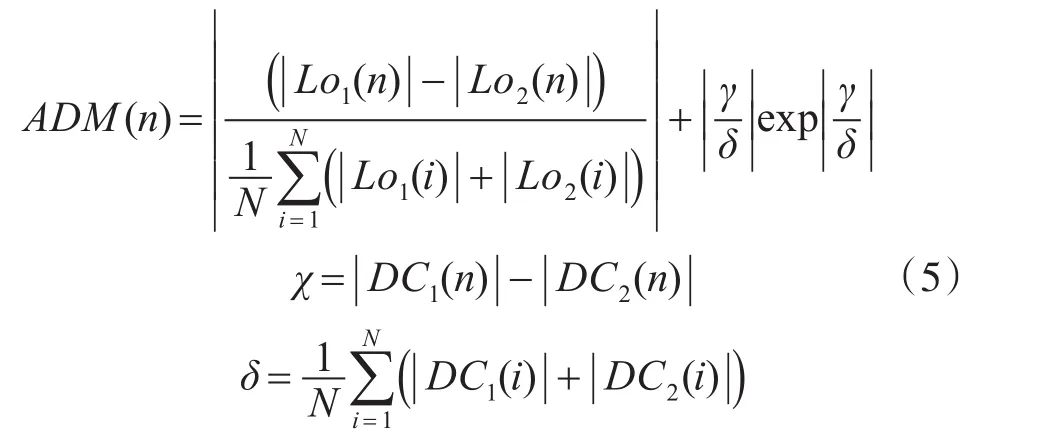
5）求導數，為計算特征差異量（FDM）做準備。一階導數采用中心差分的方式計算（Nd=2）：

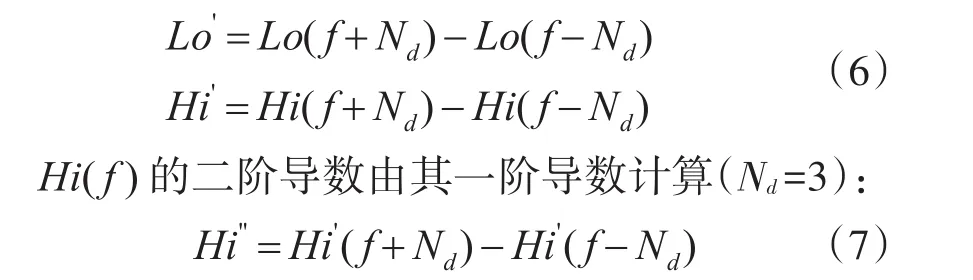
逐點計算FDM：

為了提高理論方法處理多種目標散射數據的綜合能力，擴大其適用范圍，提出了基于標準體的加權比較法，具體方法如下。

表3 FSV解釋性語言的等級尺度

8）將ADM、FDM和GDM的值轉換為等效的視覺等級描述。如表4所示，將FSV結果轉換到人類大腦所熟悉的6個數值區間（假定1為極好，6為很差），表中X為相應的逐點或平均值，而V則表示了轉換后的數值，通過變換后的V值可以判斷比對結果是偏向“好”，還是“不好”。

《嘉泰會稽志》在第九卷《山·會稽縣·會稽山》條的小字注解中，引用《舊經》說了這樣一段話：“會稽山周圍三百五十里，蓋總言東南諸山之隸會稽郡者，如晉·王彪之《刻石山詩》云‘會稽刻石山’，宋(指南北朝時期南朝宋)《何胤傳》說‘(何胤)居會稽秦望山’……刻石(山)、秦望(山)皆可以會稽山名之。《泊宅編》云：‘會稽東南巨鎮，對案梅李尖山，謂之筆案，其周回六十里’此又兼言寶山也。然則會稽云者，諸山之通稱爾”。

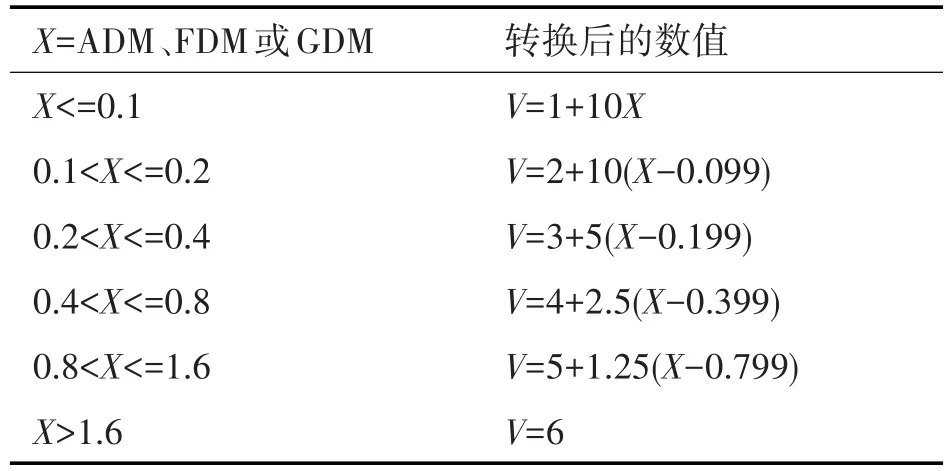
表4 FSV轉換的分段函數

4 結果分析

4.1 不同方法的評價結果

為了對以上方法的實用效果進行分析，論文選取了某海上目標的RCS仿真和實測數據，對其進行預處理并分別生成工作數據集，兩個工作數據集包含等量的數據且對應自變量相同。其中，RCS仿真數據的角度范圍為0°～359.9°，角度間隔為0.1°，RCS測量數據的角度范圍為0°～359.9°，角度間隔為0.1°，論文對兩組數據分別按角度間隔0.2°進行采樣，并截取0°～204.8°的數據，構成兩組工作數據集，數據量為1024。論文利用Matlab分別計算得到了點對點比較法、平滑比較法以及FSV方法的數據比對結果，其中平滑比較法的窗口寬度為3°，采用Matlab的moving方法進行移動平均，滑動步長為 1°。

以上數據比對方法的最終評價結果如表5和圖2～5所示。由原始數據折線圖2可見，兩組工作數據集并不完全吻合，個別尖峰值相差較大，但在總體上具有一定的相似度。而由表5的評價結果可見，點對點比較法的評價結果顯示兩組數據存在一定差異，因為個別數據相差較大導致均方誤差較大；而平滑比較法則因為對起伏較大的數據進行了平滑，對數據的評價結果好于點對點比較法。

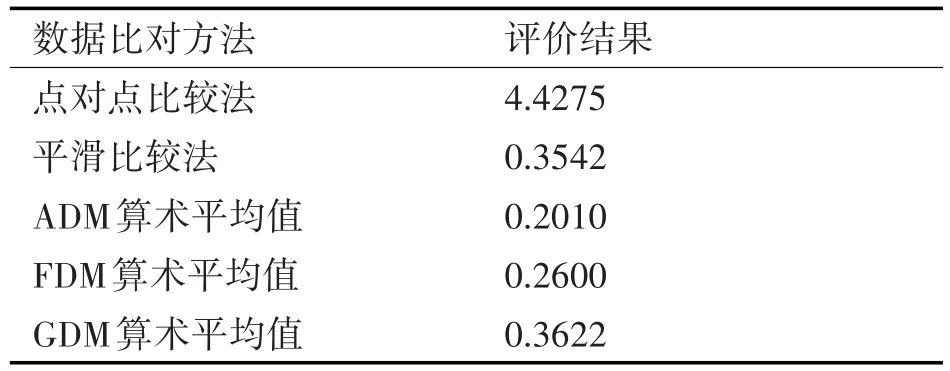
表5 幾種方法的數據比對誤差

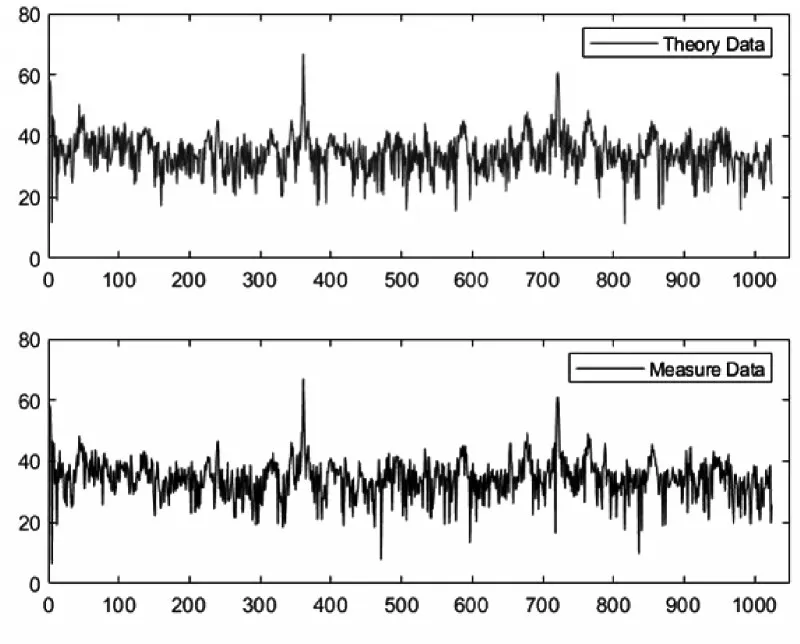
圖2 原始數據折線圖

由ADM、FDM、GDM的均值可見，FSV方法對數據的評價結果屬于“好（Good）”這個等級，而通過圖3～5能夠更加直觀看出數據相似程度的分布情況。由信任度直方圖可見，兩組工作數據集在總體數值上的一致性較好（ADM），但在數據細節上有一定差異（FDM），因此最終從全局來看兩組數據并不完全相似（GDM），根據GDM均值0.3622，由表4轉換得到V=3.8159，其值更靠近4，也就是“一般（Fail）”這個等級。

圖3 ADM信任度直方圖

圖4 FDM信任度直方圖

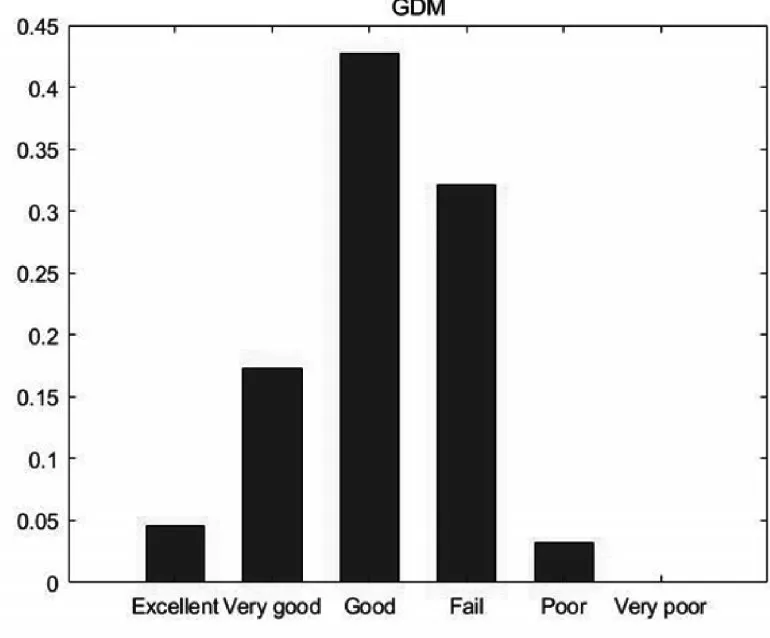
圖5 GDM信任度直方圖

4.2 不同方法的效果分析

根據上述評價結果可見，雖然某些數據比對方法可以對不同數據的差異情況做出基本的判斷，但分析結果往往并不能合理反映出差異的大小程度，因此無法實現完全的定量評估。其中，點對點比較法的優點是簡單、方便，能夠體現數據間的數值差異，但是忽略了數據的起伏趨勢變化，無法有效體現數據的動態特性；平滑比較法能夠有效去除高頻噪聲，但同樣也去除了數據的高頻特性。此外，上述方法的計算結果并不能夠準確反映現實應用所關心的數據特征差異，缺少對數據中冗余信息的剔除，其評估結果也缺少相應的模型修正或如何改進的指導信息。

相較于以上方法，FSV方法的評價結果能夠對目測評估所關注的特征要素進行提取并分別進行對比，因此對電磁仿真數據與測量數據差異的反映更加全面；其定量評估結果與專家定性評估結果建立了對應關系，可以用自然語言描述仿真結果的可信度，同時算法參數均是基于電磁仿真這一背景進行校準和設置，具有良好的適用性。

綜觀馬克思的觀點，馬克思深刻認識到了個人的發展與社會的發展是緊密相連的這一規律，社會的全面發展能夠促進個人全面發展，同樣個人的全面發展也將有力地帶動社會整體的前進。當然，這里的人的全面發展是指全社會每一個人的全面發展，而不是一部分人發展另一部分人卻不發展。

5 結語

本文針對點對點比較法、平滑比較法、加權比較法以及電磁仿真評估領域極為重要的FSV方法，通過分析以上方法的原理和計算過程，并基于已知的仿真和測量數據得到的計算結果進行了方法間的對比分析。發現除FSV方法外，雖然其他方法可以對不同數據的可信度情況做出正確判斷，但其分析結果的數值差異并不能完全反映數據差異的程度，而FSV方法可以用自然語言描述仿真結果的可信度，不僅可以較為全面地反映數據差異，同時其參數均是基于電磁仿真這一背景進行校準和設置，因此在實際模型校驗時具有良好的應用效果。