一類菌群反應擴散模型斑圖的傳播方式

夏 鵬，王 珍，李 旭

(1.江蘇聯合職業技術學院 無錫旅游商貿分院，江蘇 無錫 214045；2.云南民族大學 數學與計算機科學學院，云南 昆明 650500；3.浙江理工大學 科技與藝術學院，浙江 紹興 312369)

20世紀中葉，英國著名數學家Turing[1]首次通過生物模型解釋了自然界中動物表面產生圖案的原因，比如：斑馬、蝴蝶等.從數學的角度上來說，這是由于生物模型中的擴散項或者趨化項會使平衡態失去穩定，從而產生圖案.

最近，Tailleur[2]提出除了擴散項和趨化項能導致圖靈斑圖的產生，帶有密度抑制運動效應的生物系統通過“自我捕獲”也能產生斑圖，而后Liu和Fu[3]等通過生物實驗建立了帶有密度抑制運動效應的數學模型.當運動函數是分段函數時，Simith-Roberge[4]等構造出了這個模型的非常數定態解以及Hopf分支.Jin[5]等改進了運動函數的條件，研究了二維平面上古典解的全局存在性以及常數定態解穩定性.Wang[6]在三維平面上研究了古典解的全局存在性.當Logistic增長率為0時，Yoon[7]對于具體運動函數，研究了任意維空間上古典解的全局存在性.Xia[8]等研究了模型的亞穩性結構.而這些研究都未涉及對于具體運動函數，該模型的斑圖是通過何種方式進行傳播的？

根據文獻[9]中對趨化模型斑圖的研究思路，本文在一維空間上擬采用相似的方法對一類菌群反應擴散模型斑圖的存在性與傳播方式進行探究，從而獲得Ginzburg-Landau(GL) 型振幅方程，最后，通過數值仿真研究驗證了初始擾動產生的斑圖是通過波前方式在大區域中傳播.

1 準備工作

1.1 模型介紹

下面考慮具有密度抑制運動效應反應擴散模型[10]

(1)

模型中p(x,t)和s(x,t)分別表示大腸桿菌細胞和化學信號物質酰基高絲氨酸內酯(AHL)在位置x和時間t時刻的密度；正常數γ和d分別表示Logistic增長率和AHL的擴散速率，而大腸桿菌的擴散速率依賴于運動函數eμ(1-s),μ>0.Ω=(0，l)，l是正實數.設模型滿足諾依曼邊界條件

(2)

以及初始條件

p(x,0)=p0(x),s(x,0)=s0(x),

(3)

ν表示在邊界?Ω向外的單位向量.

1.2 斑圖的存在性

引理1[11]在一維空間Ω上，帶有齊次諾依曼邊界條件的-Δ算子的特征值和特征函數滿足：

(4)

通過簡單計算，系統(1)～(3)有2個常數解(0,0)和(1,1).在(0,0)和(1,1)處對系統進行線性化，發現(0,0)總是不穩定的，考慮到本模型是實際生物模型，不存在2種物質密度同時存在為0的情況，所以對于(0,0)情況不考慮.以下只針對常數定態解為(1,1)時研究.接下來，在(1,1)處線性化，設ωi是線性化特征值，可以得到(1,1)處的線性化特征方程為

ωi+[(1+d)λi+1+γ]ωi+(γ+λi)(1+dλi)-μλi=0,i=0,1,2,….

(5)

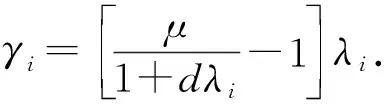
(6)

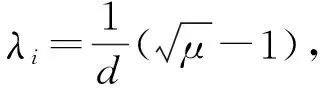
(7)

(8)

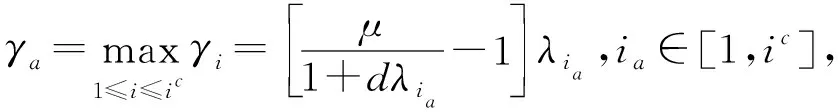
(9)

其中，ic對所有i∈[1,ic]都有γi>0成立，對所有γic+j≤0,j=1,2,….

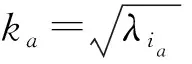
定理1假設ic滿足上述陳述，那么有以下陳述成立

a.當γ≥γc時，定態解(1,1)是線性穩定的，此時不會產生斑圖；

b.當0<γ<γa時，定態解(1,1)線性不穩定，即會產生斑圖.

2 斑圖的振幅方程

本節將應用弱非線性分析推導出描述斑圖振幅的Ginzburg-Landau 方程，考慮解對空間的依賴性，引入X作為慢變量，x作為快變量，由于斑圖解是從在常數定態解(1,1)附近分支出來的，因此做下列變換

P=p-1,S=s-1,

(10)

(11)

(12)

那么空間和時間的導數為

(13)

其中ε?1.γ和E=(P,S)T冪級數展開為

(14)

其中γa在(9)式已經定義過了，Ei=(E1i,E2i)T，T表示向量的轉置.將(14)式代入(11)式將相同階數寫在一起有

Λ(γa)E1=0,…o(ε),
Λ(γa)E2=D(E1),…o(ε2),
Λ(γa)E3=H(E1,E2),…o(ε3),

(15)

其中

(16)

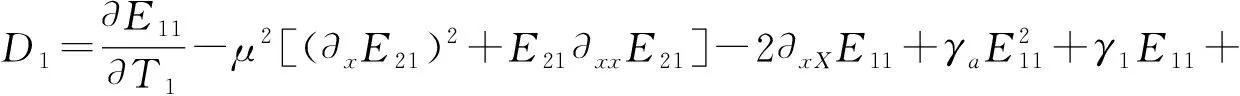
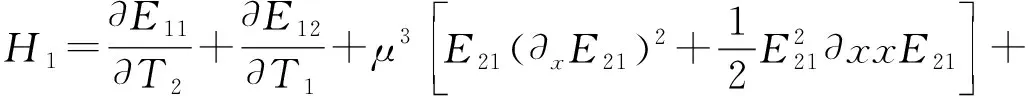
接下來利用(13)式的運算法則將(14)式代入邊界條件(2)式中，得到了在x=0,l處條件為

(17)

那么結合邊界條件(17)式，齊次線性系統(15)的第1個式子解為

(18)

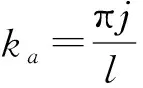
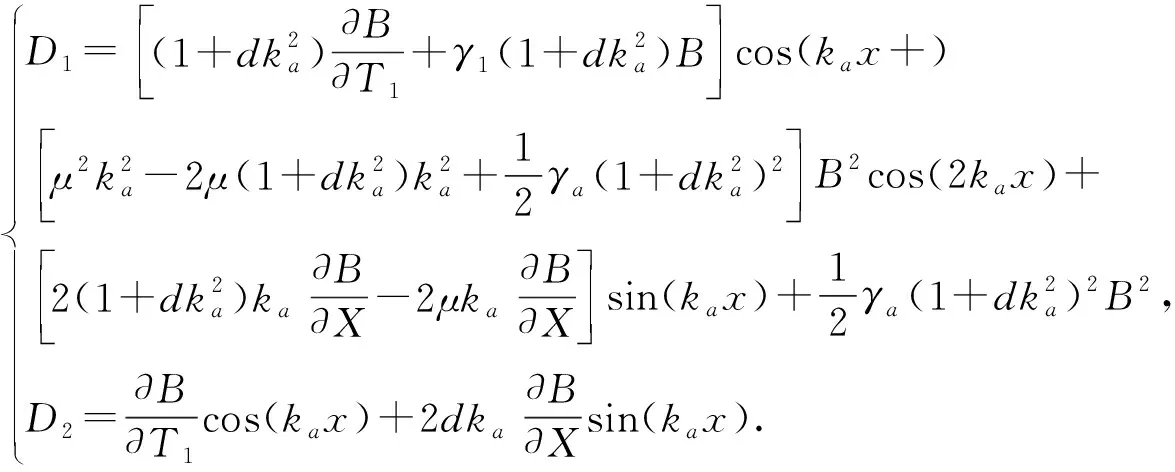
通過簡單計算(15)第1個式子的伴隨方程解的形式為

(19)

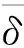
(20)

其中eij(i=1,2,j=1,2,3)分別滿足下列方程

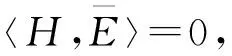
(21)

那么(21)式是經典Ginzburg-Landu 方程.應用“tanh”方法，可以找到(21)式的解為

(22)

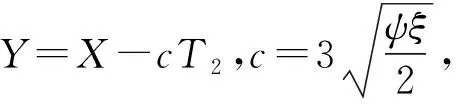
3 數值仿真

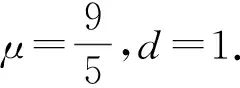
由定理1可知當γ≥γc時，系統(1)不存在斑圖，當0<γ<γa時，系統(1)會產生斑圖正如圖1和圖2所示，取γ=0.2>γc，此時沒有斑圖產生，當取γ=0.1<γa時，從圖1中明顯可以觀察到有斑圖產生.這恰好驗證了定理1的正確性.

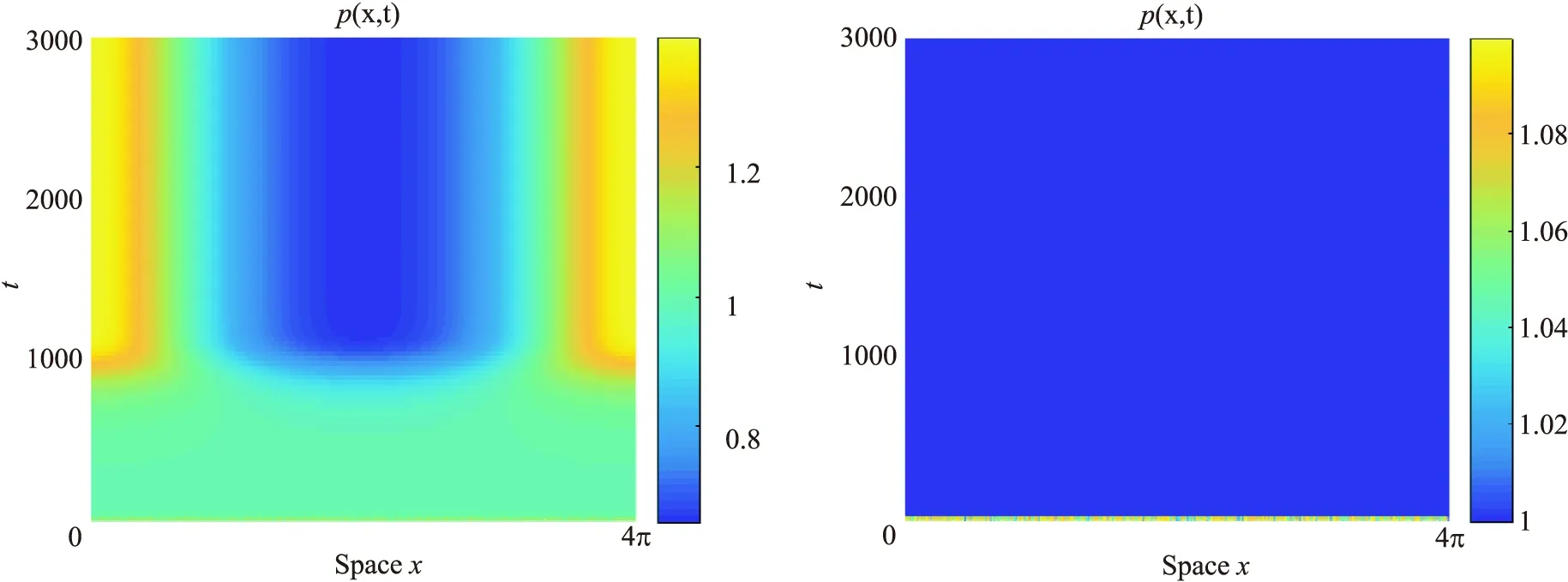
圖1 γ=0.1 圖2 γ=0.2

當γ=0.1時，圖3展現了在大區域中，常數定態解(1,1)附近的局部擾動會通過行波的形式傳播直至充滿整個區域，其中黑色實線是斑圖演變過程，紅色虛線是振幅方程(21)的數值解.從圖中可以看到振幅方程(21)很好地捕捉到了斑圖通過行波演變的過程，它的二階振幅為(0.1175,0.3067)T.這也就說明了系統(1)的斑圖是通過波前來傳播的.

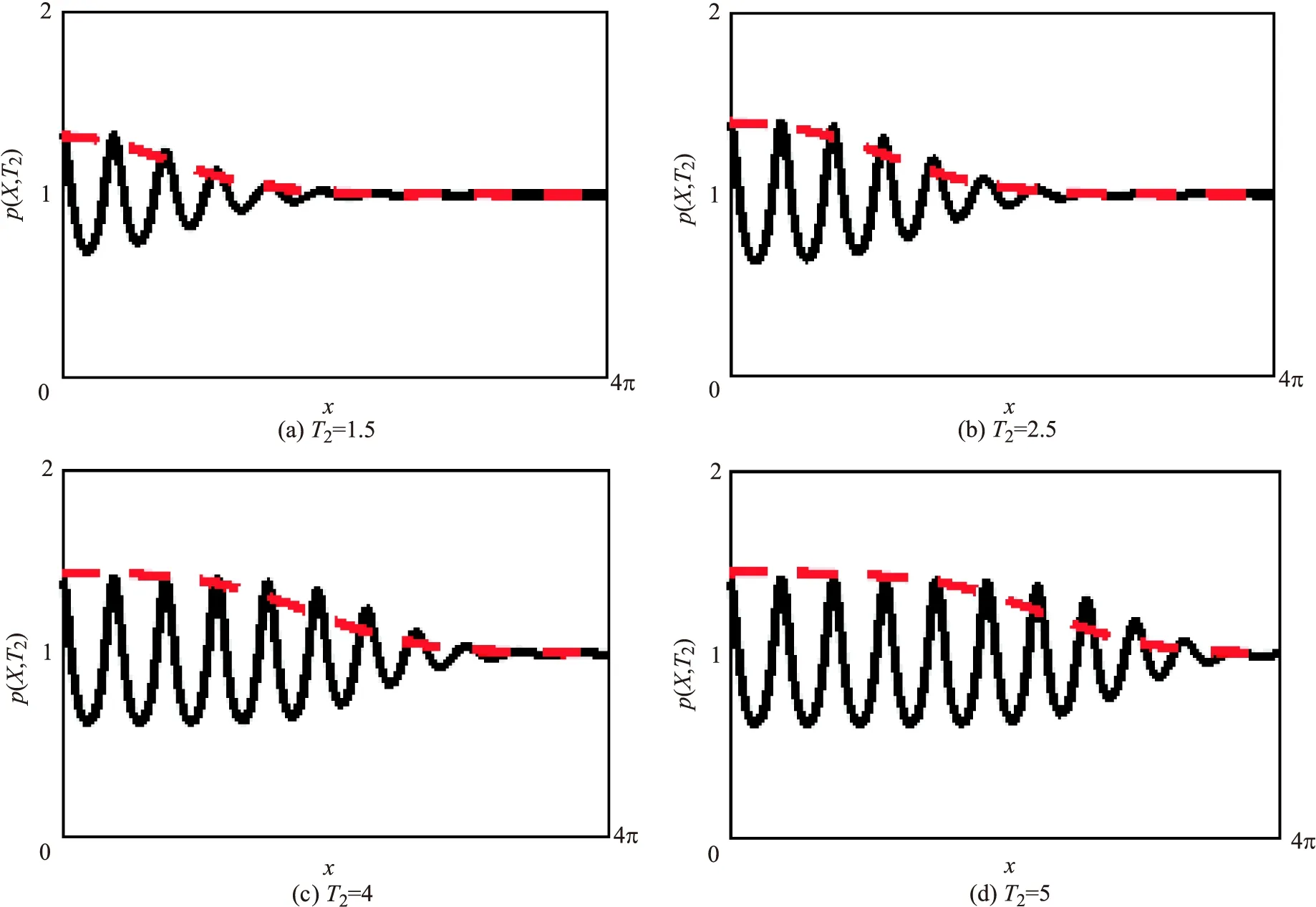
圖3 黑色實線是斑圖從左向右傳播的過程，紅色虛線是振幅方程(21)的數值解，這里γ=0.1

4 結語

文中從理論上分析了一類菌群反應擴散模型斑圖存在的條件，并且通過弱非線性分析導出了GL型斑圖振幅方程，這說明了該模型初始擾動產生的斑圖是通過波前形式傳播到整個區域.最后通過數值仿真說明了前面所得結論的正確性.