不定方程6x(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3) 的正整數(shù)解研究

王潤(rùn)青

(西南大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，重慶 400715)

不定方程也被稱為丟番圖方程,是數(shù)論中的一個(gè)重要分支,很多學(xué)者研究了形如

px(x+1)(x+2)(x+3)=qy(y+1)(y+2)(y+3)p,q∈Z+

(1)

這類方程的整數(shù)解,特別是正整數(shù)解.1971年Cohn[1]證明了當(dāng)p=1,q=2時(shí),不定方程只有一組正整數(shù)解(x,y)=(5,4);1975年P(guān)onnudurai[2]證明了當(dāng)p=1,q=3時(shí),不定方程有兩組正整數(shù)解(x,y)=(2,3),(5,7);1991年羅明[3]證明了當(dāng)p=1,q=7時(shí),不定方程只有一組正整數(shù)解(x,y)=(4,2);2017年孫浩久[4]證明了當(dāng)p=3,q=14時(shí),不定方程只有正整數(shù)解(x,y)=(5,3);以及其他更多重要結(jié)論(詳見[5],[6],[7],[8]).

文中主要運(yùn)用Pell方程,遞推序列,平方(非)剩余等初等方法證明不定方程6x(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3)僅有唯一正整數(shù)解(x,y)=(10,8),并給出所有整數(shù)解.

先將

6x(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3)，

(2)

化為

[6(x2+3x+1)]2-78(y2+3y+1)2=-42.

(3)

方程x2-78y2=-42的全部整數(shù)解可由以下兩個(gè)結(jié)合類給出:

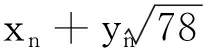
(2y+3)2=4yn+5，

(4)

(2y+3)2=-4yn+5.

(5)

又因?yàn)閥n≥-1,故(4)(5)中的yn滿足下式:

因此可推出下列關(guān)系式:

yn+1=106yn-yn-1,y0=1,y1=89.

(6)

un+1=106un-un-1,u0=1,u1=53，

(7)

vn+1=106vn-vn-1,v0=0,v1=6,

(8)

(9)

yn=un+6vn,

(10)

un+2h≡-un(moduh),vn+2h≡-vn(moduh),

(11)

yn+2h≡-yn(moduh).

(12)

接下來證明(4)當(dāng)且僅當(dāng)n=0,1時(shí)成立,(5)當(dāng)且僅當(dāng)n=0時(shí)成立,從而得到(2)的全部整數(shù)解.

1 (2y+3)2=4yn+5

本小節(jié)主要討論(2y+3)2=4yn+5為完全平方數(shù)時(shí)n的情況.

引理1設(shè)2|n,則

證因?yàn)?|n,由(8),(9)可知

un≡1(mod 2),un≡1(mod 4),4y2n+5≡4(u2n+6v2n)+5≡24v2n+5(modu2n) .

由(9)式可知

引理2設(shè)n≡0(mod 8×3)且n>0,則(4)不成立.

證令n=2·k·3·2t,2k,t≥1.

對(duì){5un±24vn}取mod 421,得到2個(gè)剩余序列周期均為15;對(duì){2t}取mod 15,得到剩余序列周期為4.

對(duì)k分2種情況進(jìn)行討論:

(1)k≡1(mod 4)時(shí),令

則有下表

表1 k≡1(mod 4) 的情況

(2)k≡-1(mod 4)時(shí),令

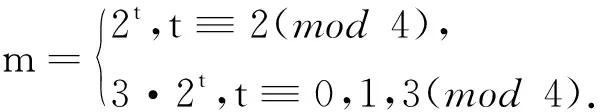
則有下表

表2 k≡-1(mod 4) 的情況

引理3設(shè)n≡1(mod 8×3)且n>1,則(4)不成立.

證令n=1+2·m·3r,r≥0,3|m,4|m.則m≡±12,±24(mod 60).

由(12),4yn+5≡-4y1+5≡-351(modum).2|m時(shí),um≡1(mod 4),得

對(duì){um}取mod 351,得到周期為350的序列,對(duì){3r}取mod 350, 得到周期為60的序列.

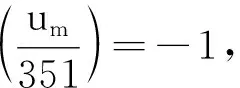
則m>0 即n>1 時(shí)(4)不成立.證畢.

推論1設(shè)n≡0,1(mod 8×3)且n>1,則(4)不成立.

引理4若(4)成立,則n≡0,1(mod 8×3).

證采用對(duì){4yn+5}取模的方法進(jìn)行證明,分為2步:

第1步 先證n≡0,1,6(mod12).

取mod 53,排除n≡3(mod 4),此時(shí)4yn+5≡20(mod 53),剩n≡0,1,2(mod 4).以上的mod 53是對(duì)序列{4yn+5}取的,mod 4是其剩余序列的周期為4,第3句是排除的理由:均為mod 53的平方非剩余.為了表述方便,后面都這樣敘述.取mod 47,排除n≡2,3,4,5,9,11(mod 12),剩n≡0,1,6,7,8,10(mod 12).取mod 239,排除n≡2,4,8,9,10,11(mod 12),剩n≡0,1,3,5,6,7(mod 12).所以n≡0,1,6(mod 12).

第2步 證n≡0,1(mod 24).

根據(jù)第1步有n≡0,1,6,18(mod 24).取mod 41,137,排除n≡0,1,4,5,7(mod 8),則n≡0,1(mod 24).證畢.

2 (2y+3)2=-4yn+5

引理5設(shè)n≡0(mod 8×3),且n>0,則(5)不成立.

證由(5)式知(2y+3)2=-4yn+5>0,由(6)式知當(dāng)n≠0時(shí)，yn>1,從而負(fù)數(shù)不可能是完全平方數(shù).當(dāng)n=0時(shí),y0=1,即-4yn+5=12.結(jié)論成立.

3 結(jié)語

定理1不定方程

x2-78(y2+3y+1)2=-42

(13)

的全部整數(shù)解是：(±x,y)=(6,0),(6,-1),(6,-2),(6,-3),(786,-11),(786,8).

證由引理2、引理3、引理4知,若(4)成立,則n=0,1,所以y=-11,-3,0,8.由引理5知,若(5)成立,則n=0,y=-1,-2.從而可以得到(13)的八組解.

定理2不定方程

6x(x+1)(x+2)(x+3)=13y(y+1)(y+2)(y+3)

(14)

的正整數(shù)解僅有(x,y)=(10,8).

證由定理1,則解出6(x2+3x+1)=±6,±786,即x2+3x+13=±1,±131,x=-13,-3,-2, -1,0,10.可得到(14)的全部整數(shù)解:(-3,-3),(-3,-2),(-3,-1),(-3,0),(-2,-3),(-2,-2),(-2,-1),(-2,0),(-1,-3),(-1,-2),(-1,-1),(-1,0),(-13,-11),(-13,8),(10,-11),(10,8).其中,正整數(shù)解只有(x,y)=(10,8).