作圖分析法

黃旭軍

阿木老師進教室時，正好碰到“小老師”李宏宇給同學講題目。“小老師”并不好當，李宏宇講得鼻尖上汗珠直冒，嘴上怪叫……對面的同學還是一臉茫然，甚至表現出快要暈倒的樣子。

“小老師”嘆了口氣，道：“我都講了六遍了，你怎么就不會呢？”

“什么題目這么難，讓我們班‘小老師長吁短嘆的？”阿木老師也來湊熱鬧。

“就是這道題，他就是不理解，講了六遍也沒用！”李宏宇指著一道題：兩個數相乘，一個因數增加6，積就增加24;另一個因數增加8，積也增加24，這兩個因數的積是多少？

阿木老師哈哈一笑，說：“你一定沒有畫圖！”于是他在草稿紙上畫了個長方形，接著“唰唰”幾下，就改出了這樣一題：有一個長方形，寬增加6厘米，面積增加了24平方厘米;長增加8厘米，面積增加了8平方厘米。原來的面積是多少？

一直沒學會的那位同學恍然大悟：“24÷6=4（厘米），正好就是長方形的長！24÷8=3（厘米），正好是長方形的寬！3×4=12（平方厘米）就是原長方形的面積！”

例1

8個相同的瓶子中，有7瓶是普通的水，有1瓶是麻醉藥。喝下麻醉藥的生物都會在1小時之內昏迷。現在，你只有3只小白鼠和1小時的時間，如何檢驗出哪個瓶子里有藥？

8個瓶子的溶液，用3只小白鼠來測試，瓶子外形一樣，要標上符號才能區別。

我們用二進制給每個瓶子編號，編號分別為000，001，010，011，100，101，110，111。然后讓第1只老鼠喝編號第1位數字為1的水，第2只老鼠喝編號第2位數字為1的水，第3只老鼠喝編號第3位數字為1的水。假設第4瓶水有藥，即011有藥。

第1只老鼠喝了 100，101，110，111瓶子中的水，結果：沒昏迷，記作0。

第2只老鼠喝了 010，011，110，111瓶子中的水，結果：昏迷，記作1。

第3只老鼠喝了 001，011，101，111瓶子中的水，結果：昏迷，記作1。

根據昏迷結果，剛好是第4瓶水011，其他情況推理類同。

用作圖法來分析，這道題用韋恩圖最適合。

首先給8個瓶子編號：1，2，3，4，5，6，7，8，再給3只小白鼠編號：A，B，C。

用大圈表示小白鼠，畫圖：

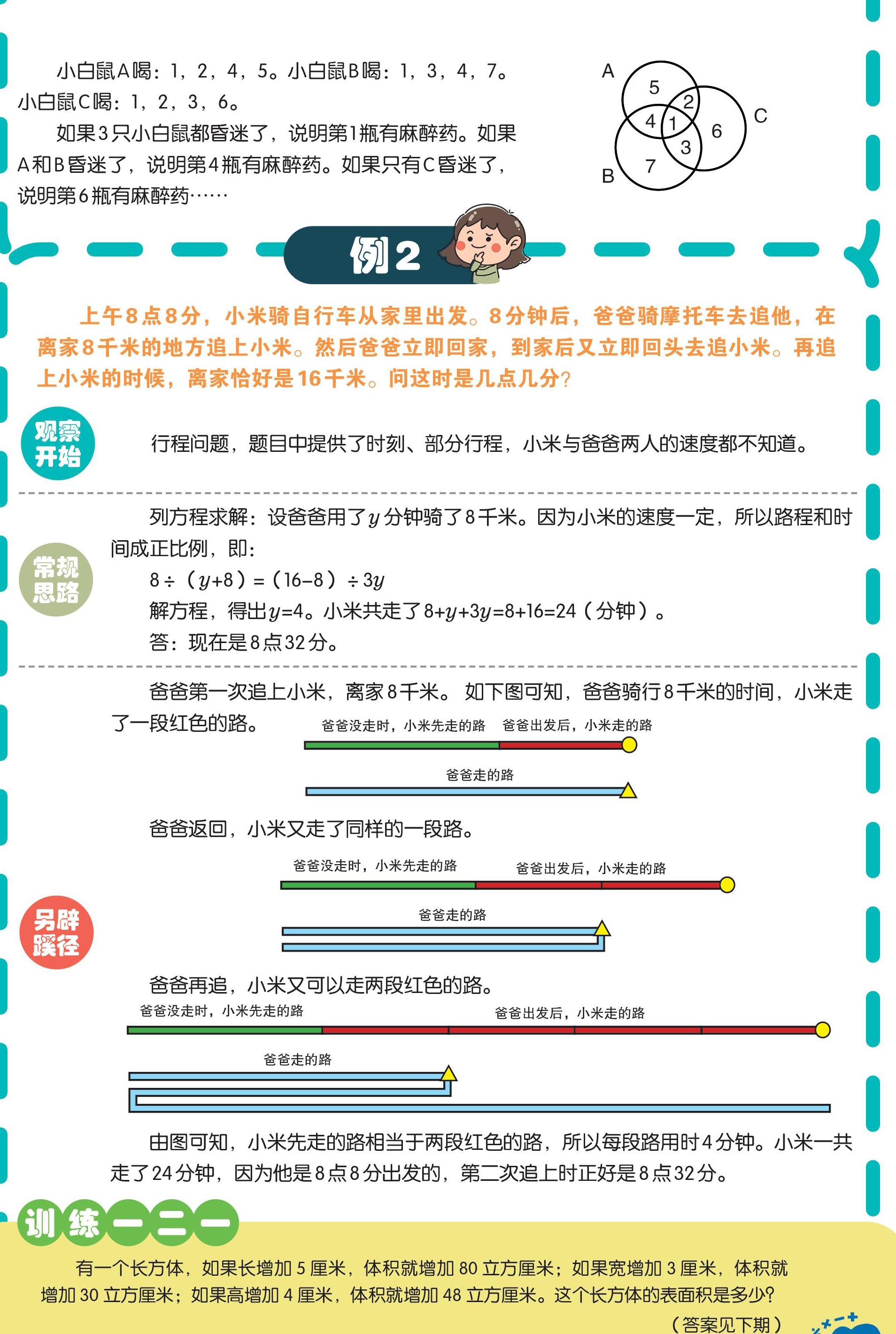
小白鼠A喝：1，2，4，5。小白鼠B喝：1，3，4，7。小白鼠C喝：1，2，3，6。

如果3只小白鼠都昏迷了，說明第1瓶有麻醉藥。如果A和B昏迷了，說明第4瓶有麻醉藥。如果只有C昏迷了，說明第6瓶有麻醉藥……

例2

上午8點8分，小米騎自行車從家里出發。8分鐘后，爸爸騎摩托車去追他，在離家8千米的地方追上小米。然后爸爸立即回家，到家后又立即回頭去追小米。再追上小米的時候，離家恰好是16千米。問這時是幾點幾分？

行程問題，題目中提供了時刻、部分行程，小米與爸爸兩人的速度都不知道。

列方程求解：設爸爸用了y分鐘騎了8千米。因為小米的速度一定，所以路程和時間成正比例，即：

8÷（y+8）=（16-8）÷3y

解方程，得出y=4。小米共走了8+y+3y=8+16=24（分鐘）。

答：現在是8點32分。

爸爸第一次追上小米，離家8千米。 如下圖可知，爸爸騎行8千米的時間，小米走了一段紅色的路。

爸爸返回，小米又走了同樣的一段路。

爸爸再追，小米又可以走兩段紅色的路。

由圖可知，小米先走的路相當于兩段紅色的路，所以每段路用時4分鐘。小米一共走了24分鐘，因為他是8點8分出發的，第二次追上時正好是8點32分。

有一個長方體，如果長增加5厘米，體積就增加80立方厘米;如果寬增加3厘米，體積就增加30立方厘米;如果高增加4厘米，體積就增加48立方厘米。這個長方體的表面積是多少？

（答案見下期）