橢球各向異性介質彈性波完全解耦波動方程
梁 鍇 曹丹平 孫上饒 印興耀
(中國石油大學(華東)地球科學與技術學院,山東青島 266580)
0 引言
彈性波波動方程解耦在彈性波傳播理論和實際應用中具有非常重要的意義。在均勻彈性各向同性介質中,對矢量彈性波動方程分別通過求散度和旋度運算,使縱波和橫波分離成兩個獨立傳播過程,稱為縱波與橫波在矢量場中的解耦現象[1],即縱波與橫波兩種波動獨立存在,分別滿足各自獨立傳播的波動方程。在大多數各向異性介質中,縱波、橫波是耦合在一起傳播,描述彈性波傳播的方程非常復雜,通常難以解耦,要采用特殊的方法進行處理才能得到各向異性介質中獨立傳播的縱波、橫波波動方程。Alkhalifah[2-3]提出了基于聲學假設的VTI介質和OA介質qP波波動方程;Grechka等[4]研究了各向異性介質中的橫波波動方程;Zhou等[5]利用二維TTI介質qP波方程進行了模擬和偏移;梁鍇等[6]從頻散關系出發研究了三維TTI介質中波動方程的分解;Fowler等[7]對多個聲學假設的qP波方程進行了對比和分析;Duveneck 等[8]和Zhang等[9]分別提出了TTI介質穩定的qP波方程;Cheng等[10-11]利用偏振方向投影方法推導了各向異性介質純qP波和qSV波方程;郭成鋒等[12]利用改進的TTI介質純P波方程進行了正演模擬和逆時偏移;慕鑫茹等[13]基于最佳平方逼近方法進行了TTI介質qP波與qSV波的解耦研究;谷一鵬等[14]利用擴展各向異性線性近似研究了VTI介質qP波和qSV波解耦的相速度近似表征;孫上饒等[15]基于近似配方法研究了三維TTI介質qP波和qSV波解耦的相速度和群速度近似表征。
橫向各向同性(TI)介質是常見的各向異性介質,是薄互層儲層或裂縫儲層地震資料處理和解釋中常用的模型[16-19]。當TI介質的Thomsen參數滿足ε=δ時,被稱為橢球各向異性(EA)介質。EA介質的獨立彈性常數只有4個。Bakulin等[20]研究表明含氣裂縫介質可以等效為橢球各向異性介質,因此開展橢球各向異性介質的研究具有重要的應用價值。Byun[21]研究了基于射線理論的橢球各向異性介質的地震參數;Helbig[22]總結了橢球各向異性介質彈性波波前傳播特征和SH波反射透射特征;Thomsen[23]給出了橢球各向異性介質的Thomsen參數表征;李磊等[24]討論了橢球各向異性介質的約束條件;梁鍇等[25]分析了傾斜橢球各向異性介質(TEA)彈性波傳播特征,發現在TEA介質中qP波和qSV波的相速度是精確解耦的。
本文在梁鍇等[25]的研究基礎上,分析了EA介質彈性波的頻散關系和波動方程解耦。從EA介質彈性波波動方程出發,將彈性波頻散關系進行因式分解,推導了EA介質完全精確解耦的qP波、qSV波和SH波波動方程,分別描述三種波的獨立傳播,在此基礎上進行了正演模擬并給出了數值示例。
1 EA介質剛度矩陣
各向異性介質中,應力與應變之間線性關系的比例系數由剛度矩陣C確定,而由C表征的彈性波動方程系數的物理意義很不直觀。為方便理論研究和實際應用,Thomsen[23]提出了一套表征TI介質彈性性質的參數,與C的關系可表示為
(1)
式中:VP0、VS0分別為qP波和qS波沿對稱軸方向的相速度;ρ為密度;ε是度量qP波各向異性強度的參數;δ近似表征TI介質對稱軸方向qP波相速度對傳播角度的二階導數;γ是度量SH波各向異性強度或橫波分裂強度的參數。
當ε=δ或(C13+C44)2=(C11-C44)(C33-C44)時,TI介質退化為EA介質,其Thomsen參數與C的關系為
在本構坐標系下,EA介質的剛度矩陣為
(3)
2 EA介質解耦波動方程
波動方程的頻散關系在波動方程解耦、單程波方程推導等方面起著非常重要的作用。在各向異性介質中,通過求解Christoffel方程不僅可得到彈性波傳播的相速度與群速度,還可求解出EA介質彈性波的精確頻散關系方程。
利用EA介質剛度矩陣C,結合彈性動力學的本構方程、運動平衡微分方程和幾何方程,可得EA介質彈性波波動方程
(4)
式中:u=(ux,uy,uz)T,為位移矢量;F=(Fx,Fy,Fz)T,為體力項。設彈性波方程(式(4))的平面波解為
u=pexp[i(kxx+kyy+kzz-ωt)]
(5)
式中:kx、ky、kz分別為x、y、z方向的波數;p=(px,py,pz)T,為平面波的偏振向量;ω為圓頻率。
將平面波解代入EA介質波動方程(式(4)),并忽略體力項的影響,可得EA介質Kelvin-Christoffel方程
(6)
式中
(7)
要使式(6)有非零解,必須使其行列式為零,即
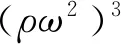
(8)
整理式(8),可得EA介質彈性波精確頻散關系
(9)
式(9)可因式分解為三個獨立的頻散方程,分別是EA介質qP波、qSV波和SH波的解耦頻散方程
(10)
EA介質解耦的波動方程可由EA介質頻散關系方程通過Fourier反變換得到,即
(11)
(12)
(13)
式(11)~式(13)由EA介質精確的頻散關系解耦導出,沒有利用弱各向異性近似或聲學假設近似,因此解耦的方程既適合弱各向異性EA介質,也適合強各向異性EA介質。解耦的qP波方程(式(11))只與VP0、ε有關,與VS0、γ無關;解耦的qSV波方程(式(12))與各向同性介質的橫波方程相同,只與VS0有關,與VP0、ε、γ無關,說明在EA介質中qSV波的速度或波前面是各向同性的。解耦的SH波方程(式(13))只與VS0、γ有關,與VP0、ε無關。
當EA介質退化為各向同性介質(ε=γ=0)時,式(11)~式(13)也退化為各向同性介質P波和S波的波動方程。
3 數值示例
為了驗證EA介質彈性波完全解耦波動方程的正確性和有效性,設計了兩個均勻EA介質模型。兩個模型的VP0、VS0、ρ相同,分別為3000m/s、1732m/s、2000kg/m3;第一個模型ε=γ=0.2,為弱各向異性介質;第二個模型ε=γ=1.0,為強各向異性介質。采用高階有限差分算法進行正演模擬。
圖1為根據EA介質彈性波群速度公式[25]計算的250ms時刻理論波前面,可見,在xOz面和yOz面內,qP波和SH波波前為橢圓狀,而qSV波為圓形,而在xOy面三種波的波前均為圓形。圖2為弱各向異性EA介質彈性波波動方程的模擬結果,可見,在集中力源激發的彈性波場中包含qP波、qSV波和SH波,qP波和SH波的波前面為橢球狀,qSV波波前面為球狀,即EA介質中qSV波的速度是各向同性的。圖3為EA介質完全解耦波動方程的模擬結果,由圖可見,解耦的qP波場不含有qSV或SH成分,qSV波場不含有qP或SH波成分,SH波波場不含有qP或qSV成分。對于EA介質解耦方程的波場,qP波和SH波的波前面為橢球狀,qSV波波前面為球狀,說明解耦方程的運動學特征與彈性波方程保持一致,數值模擬結果與理論曲線完全吻合。
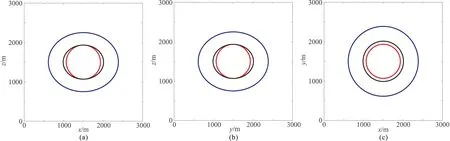
圖1 弱各向異性EA模型彈性波250ms時刻理論波前面(a)xOz面;(b)yOz面;(c)xOy面。藍線表示qP波;黑線表示SH波;紅線表示qSV波

圖2 弱各向異性EA模型彈性波方程模擬的250ms時刻波場快照(a)ux;(b)uy;(c)uz。左為xOz面;中為yOz面;右為xOy面

圖3 弱各向異性EA模型完全解耦方程模擬的250ms時刻波場快照(a)uP;(b)uSV;(c)uSH。左為xOz面;中為yOz面;右為xOy面
圖4為強各向異性EA模型彈性波250ms時刻理論波前面,圖5為強各向異性EA介質彈性波波動方程的模擬結果,圖6為強各向異性EA介質完全解耦波動方程的模擬結果,數值模擬結果與理論曲線完全吻合。圖1~圖6說明這三個完全解耦的波動方程不僅適用于弱各向異性EA介質,也同樣適合強各向異性EA介質。同時,EA介質的各向異性越強,qP波和SH波波前面的橢球扁率就越大。
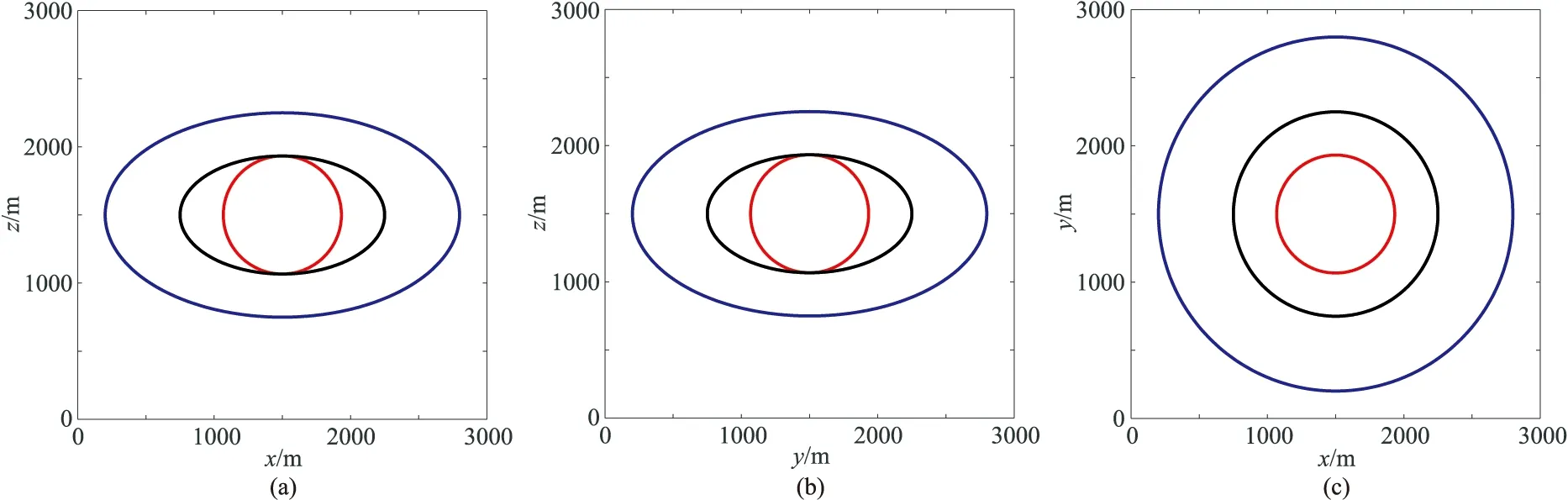
圖4 強各向異性EA模型彈性波250ms時刻理論波前面(a)xOz面;(b)yOz面;(c)xOy面。藍線為qP波;黑線為SH波;紅線為qSV波

圖5 強各向異性EA模型彈性波方程模擬的250ms時刻波場快照(a)ux;(b)uy;(c)uz。左為xOz面;中為yOz面;右為xOy面

圖6 強各向異性EA模型完全解耦方程模擬的250ms時刻波場快照(a)uP;(b)uSV;(c)uSH。左為xOz面;中為yOz面;右為xOy面
4 結論與認識
一般來說各向異性介質中縱波和橫波是耦合傳播的,但EA各向異性介質卻是一個例外。本文從EA介質精確頻散關系方程出發,利用因式分解方法將其分解為三個解耦的頻散方程,然后利用傅里葉反變換得到了EA介質完全精確解耦的qP波、qSV波和SH波的波動方程。解耦方程表明,在均勻EA介質中,qP波、qSV波和SH波可以完全解耦,三種波可以獨立傳播。理論公式和數值模擬均表明,這三個完全解耦方程不僅適用于弱各向異性EA介質,也同樣適合強各向異性EA介質。另外,均勻EA介質中qP波和SH波的波前面為橢球狀,qSV波的波前面為球狀,且qSV波的波前面與各向異性參數無關。
因為傾斜含氣裂縫地層可以等效為傾斜橢球各向異性(TEA)介質,本文研究的EA介質是TEA介質對稱軸垂直時的特例,因此關于TEA介質彈性波頻散關系和解耦波動方程、地震波在傾斜含氣裂縫地層中的傳播規律,是今后的研究方向。

