時間域廣義2.5D一階波動方程曲網格有限差分法數值模擬

楊尚倍 白超英 ZHOU Bing

(①中國地質調查局西安地質調查中心，陜西西安 710054；②長安大學地質工程與測繪學院地球物理系，陜西西安 710054；③哈利法科學與技術大學地球科學系，阿布扎比 2533)

0 引言

地震波場數值模擬不僅是了解地震波傳播規律和解釋地震數據的重要工具，也是地震成像的基礎。隨著計算機技術快速發展，各種地震波場數值模擬算法日趨完善，如有限差分法[1]、有限元法[2]、邊界元法[3]、偽譜法[4-5]、譜元法[6]、有限體積法[7]等。盡管3D波場數值解相對于2D更符合實際觀測記錄，然而巨大的內存需求和運算量使得實際3D大尺度波場數值模擬及波形反演面臨計算資源的巨大挑戰。因此，目前更多的實際應用則在2D或小尺度的3D空間開展，如逆時偏移成像[8]和全波形反演[9]。

雖然2D數值模擬相較于3D高效，但引入了線源假設代替實際的點源激發。這種線源假設意味著震源激發大小沿走向不變，模擬的波場也是2D，其結果很難與實際觀測的3D地震記錄相匹配[10-11]。當然可采用3D到2D地震數據轉換方法，將實際的點源數據(3D)轉換成線源數據(2D)，但目前這些轉換方法只適用于簡單的地質模型，例如均勻介質和水平層狀介質，并且需要滿足遠場近似和無波場重疊等苛刻條件[12]，不利于實際復雜介質的成像。

鑒于此，為了克服2D波場模擬中線源假設帶來的失真和3D波場模擬中效率低下的不足，人們提出了2.5D波場模擬方法[13]。2.5D地震波場數值模擬方法假設地質模型沿走向方向模型屬性不變，因此可以沿走向方向做傅里葉變換將3D問題簡化為重復的2D問題，從而大大提高了計算效率，且與3D解析解高度吻合[14]。如：Song等[13]在頻率域通過有限差分法重構了3D地震波場；Zhou等[15]給出了精確的2.5D吸收邊界條件，并采用有限元法得到了頻率域2.5D波場數值解；Maokun等[16]則利用近似最佳正交有限差分算法進行了2.5D彈性波數值模擬；Takenaka等[17]給出了時間域平面波入射下2.5D彈性波動力學方程的求解過程；Novais等[18]改進了時間域2.5D地震波場有限差分數值模擬方法的波數采樣方法。Xiong等[19]首先將空間域彈性波方程轉換為波數域彈性波方程，然后采用交錯網格有限差分求解波數域方程。

然而，上述時間域或頻率域2.5D地震波場數值模擬方法只針對單一的彈性、黏彈性或各向異性介質，并沒有一種較為普適的算法，即可同時滿足不同介質屬性(彈性、黏彈性、各向異性)和不同邊界條件(聲波自由地表，固體自由地表和固—液邊界)下的2.5D波場數值模擬算法。本文提出一種適合復雜多種介質混合模型下時間域廣義2.5D一階波動方程及數值解法，適用于混合(聲波、彈性各向同性、彈性各向異性)介質和各種邊界條件(聲波自由地表、固體自由地表和固—液邊界)的地震波場數值模擬。

另一方面，為了適應復雜地表起伏模型中的數值模擬，本文采用曲網格進行模型剖分，并采用低頻散、低耗散的同位網格MacCormack有限差分法格式[20]離散時間域廣義2.5D一階波動方程，從而得到高精度的數值解。最后，應用數值模擬算例驗證了本文2.5D數值模擬方法的正確性和有效性。

1 時間域2.5D廣義一階速度—應力 波動方程

首先建立廣義2.5D一階速度—應力波動方程，并分析該方程的普適性問題。2.5D地震波場數值模擬是3D地震波場數值模擬的一種特殊情況，其假設地質模型沿走向(y方向)具有不變的物理性質，則2.5D地震波動方程可以通過對3D地震波動方程沿y方向做傅里葉變換得到[21]。

1.1 彈性各向異性介質波動方程

三維彈性各向異性介質中，地震波的控制方程[22]為

(1)

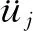
σ=cu

(2)

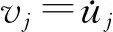
(3)

和

(4)

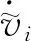
(5)

式中上標“(S)”表示彈性各向同性或彈性各向異性的固體介質。式(3)和式(4)可簡寫為矩陣形式

(6)

上式為任意彈性各向異性介質中的2.5D地震波控制方程，系數矩陣A(S)、B(S)、C(S)的具體表達式見附錄A。

1.2 聲波介質波動方程

在聲波介質中，應力滿足切向應力為零和法向應力的軸向分量等于液體壓力

σij=-δijP

(7)

P可表示為

P=-Kuj,j+s(t)δ(x-xs)

(8)

式中：K為體積模量；s(t)為xs處的震源函數。將式(7)代入式(1)，可得

(9)

對式(8)求時間導數，可得

(10)

根據式(9)，式(10)可以表示為

(11)

對式(9)和式(11)做關于y的傅里葉變換，可得

(12)

(13)

定義

(14)

可得式(12)和式(13)的矩陣形式

(15)

式中：上標“(W)”表示聲波介質；系數矩陣A(W)、B(W)、C(W)的具體表達式見附錄B。上式為聲波介質中的2.5D地震波控制方程。

1.3 聲波自由地表

聲波自由地表邊界條件需要滿足地表處液體壓力P=0，代入式(12)和式(13)，可得

(16)

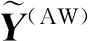
(17)

式中：上標“(AW)”表示聲波自由地表；系數矩陣A(AW)、B(AW)、C(AW)分別為

(18)

(19)

C(AW)=0

(20)

對比式(18)～式(20)與附錄B，可以發現式(17)是式(15)的特例。

1.4 固體自由地表

固體自由地表邊界條件需要滿足地表處法向應力為0，即

σ·n=0

(21)

展開為

(22)

式中n=(n1，n2，n3)表示界面的法向向量。將式(22)寫成矩陣形式

(23)

將上式寫為子矩陣格式

Γ2σ2=-Γ1σ1

(24)

式中

(25)

(26)

定義

(27)

式(23)可改寫為

σ2=Sσ1

(28)

由上式可知，應力分量σ2可由σ1和表面法向分量n得到，只有應力分量σ1未知。假設自由地表由z=z0(x)給出，其坡度為tanα=z′0(x)，法向分量為n=(-sinα,0,cosα)，則式(27)變為

(29)

根據式(28)和式(29)可得

(30)

將上式代入式(3)，可得

(31)

由式(4)可得

(32)

定義

(33)

則式(30)和式(31)可簡寫為

(34)

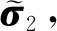
1.5 固—液邊界

在固—液邊界上，例如由z=z0(x)定義的二維海底界面，邊界條件需要滿足法向應力和法向速度分量連續，并且切向應力分量為0，即

(35)

(36)

(37)

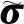
(38)

將式(38)代入(37)，可得

(39)

(40)

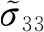
(41)

為了表示簡單，假設固液邊界上沒有施加震源，將式(4)和式(13)代入(41)，可得

(42)

上式對于任意ky成立，可得

(43)

由式(35)可知

(44)

將式(42)代入式(4)，可得

(45)

將式(39)和式(40)代入式(3)，可得

(46)

式中ρS為固體密度。由式(12)可知

(47)

式中ρW為液體密度。定義

(48)

將式(45)～式(47)寫成矩陣形式

(49)

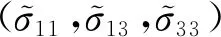
至此，獲得了2.5D廣義一階速度—應力波動方程

(50)

式中的各個參量可根據不同介質或不同邊界條件而有所不同。

2 曲線網格有限差分算法

2.1 曲線坐標系與直角坐標系的轉換關系

為了使網格線與物理空間的邊界線重合，避免傳統矩形網格由于階梯狀近似產生的虛假散射問題，應用曲線網格(貼體網格)對地質模型進行剖分，然后將實際的非規則物理空間變換到一個規則的計算空間[23]。假設物理空間的坐標(x,z)和計算空間的坐標(ξ,η)之間映射關系(圖1)為

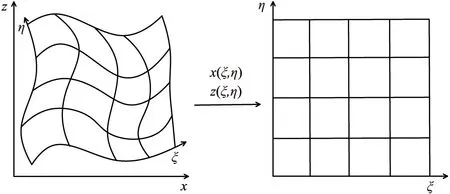
圖1 曲線網格和計算網格的變換關系示意圖

(51)

由鏈式求導法則可得

(52)

整理可得到坐標轉換系數

(53)

式中J=x,ξz,η-x,ηz,ξ。為了避免網格非均勻引發的虛假震源項，x,ξ、x,η、z,ξ、z,η均采用數值方法計算，所采用的數值法與下文求解波動方程空間導數的數值算法相同。

2.2 曲線坐標系中的廣義一階速度—應力波動方程

根據求導的鏈式法則，廣義一階速度—應力彈性波方程的矩陣形式在曲線坐標系中的表達式為

(54)

Hixon等[24]采用Tam等[25]提出的DRP (Dispersion Relation Preserving)方法對同位MacCormack格式的系數進行了優化，得到了低頻散、低耗散的DRP/opt MacCormack 格式，本文采用該格式有限差分算子離散方程。

同位網格MacCormack格式的兩個偏心差分格式——向前和向后差分格式分別為

(55)

(56)

差分系數為

(57)

采用DRP/opt MacCormack有限差分格式，式(54)空間導數可以離散為

(58)

在時間方向上采用四階Runge-Kutta法[26]，結合DRP/opt MacCormack有限差分算子，波場可以從時間步長第N步更新到第N+4步[20]，具體過程如下。

(59)

(60)

(61)

(62)

式中：α1=0.5；α2=0.5；α3=1.0；β1=1/6；β2=1/3；β3=1/3；β4=1/6。

3 震源、人工邊界和波數域采樣

3.1 震源和吸收邊界

本文在網格點上施加集中力源，并使用Ricker子波做為震源

(63)

式中：震源中心頻率fc=30Hz；延遲時間t0=30ms。為了消除人工邊界產生的邊界反射，本文采用新近提出的廣義剛度衰減法(The Generalized Stiffness Reduction Method，GSRM)[27]，吸收效果優于最佳匹配層方法，適用于各種介質，如聲波介質、各向同性和各向異性介質。

3.2 波數域采樣方法

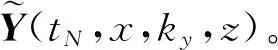
(64)

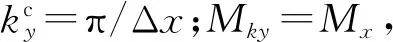
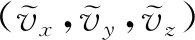
(65)

式中vij表示施加i方向集中力源時得到的j方向速度分量。

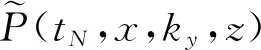
(66)

4 2.5D與3D數值模擬的精度和效 率分析

表1 介質彈性參數

圖2為三個地表水平均勻介質模型的2.5D數值解的波場快照，從圖中可以清晰地看到波場的P、S波波前。為了驗證本文方法模擬得到的2.5D數值解的計算精度和正確性，將2.5D數值解與對應的3D解析解及3D數值解進行對比(圖3)，三者匹配良好，驗證了本文算法的計算精度和正確性。

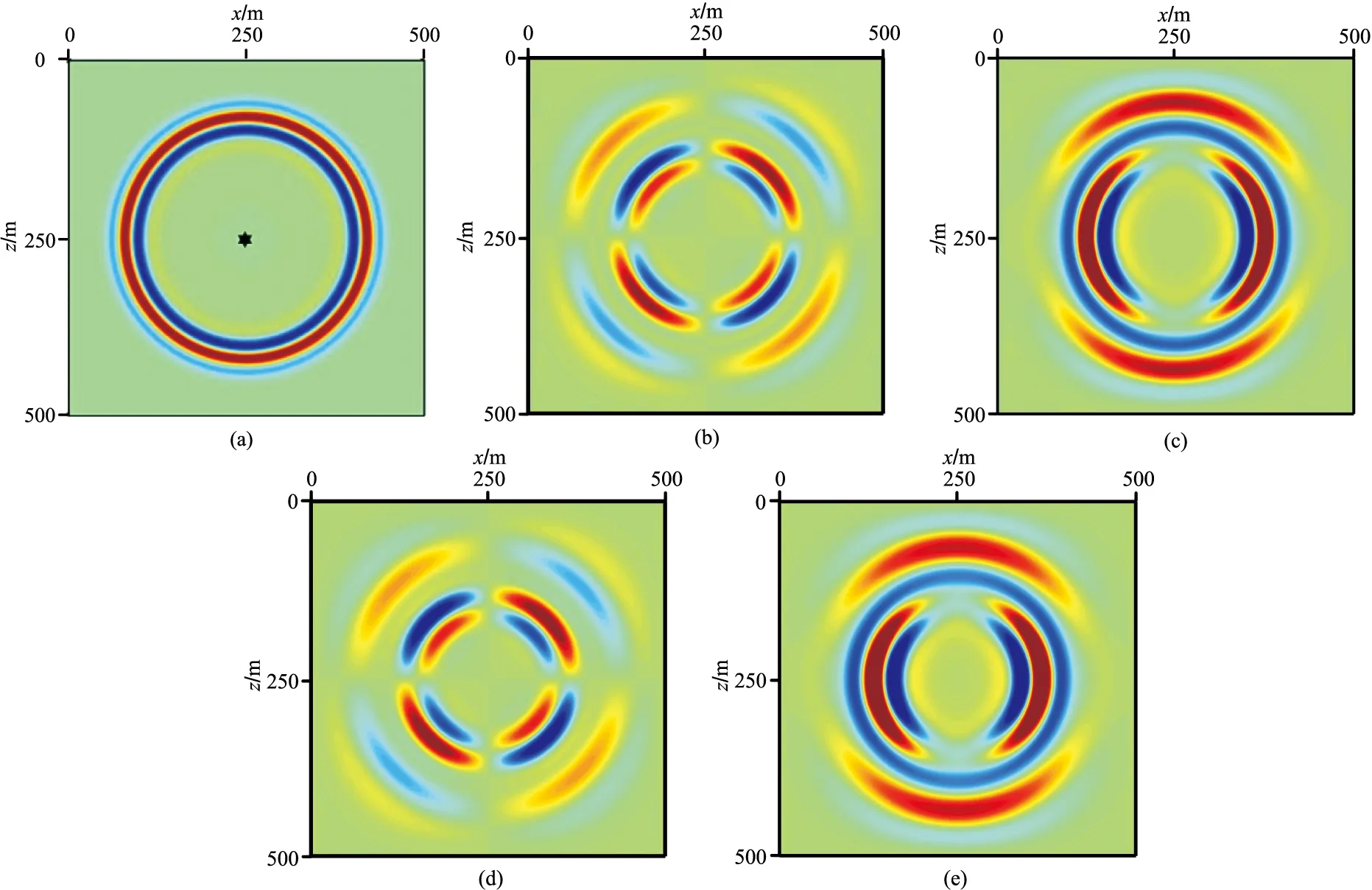
圖2 地表水平均勻介質模型2.5D模擬的波場快照(a)聲波介質的P分量，0.15s；(b)、(c)分別為各向同性介質的vx和vz分量，0.09s；(d)、(e)分別為VTI-1介質的中vx和vz分量，0.08s

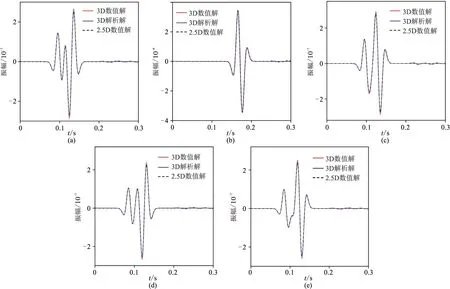
圖3 地表水平均勻介質模型2.5D數值解與3D數值解、3D解析解的對比(a)聲波介質中P分量；(b)、(c)分別為各向同性介質的vx和vz分量；(d)、(e)分別為VTI-1介質的vx和vz分量

2.5D與3D數值模擬計算機內存占用和CPU運行時間的對比如表2所示，可以看出，2.5D數值模擬所需CPU時間和計算機內存都遠小于3D，特別是計算機內存。所以本文的2.5D波場數值模擬方法則具有較高的實際應用價值，可以直接應用于地震數據反演方法。

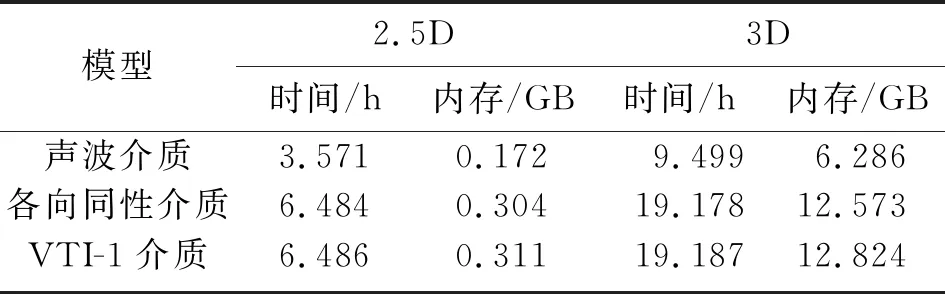
表2 2.5D與3D數值模擬用時和內存占用對比

5 復雜模型的波場數值模擬

5.1 起伏地表均勻模型

應用起伏地表聲波、彈性各向同性和彈性VTI-1均勻介質模型(圖4)驗證本文施加自由地表邊界算法的正確性。網格剖分間距Δx=Δz=2m，震源位于(500m，400m)，檢波器位于(300m，500m)，模型參數見表1。

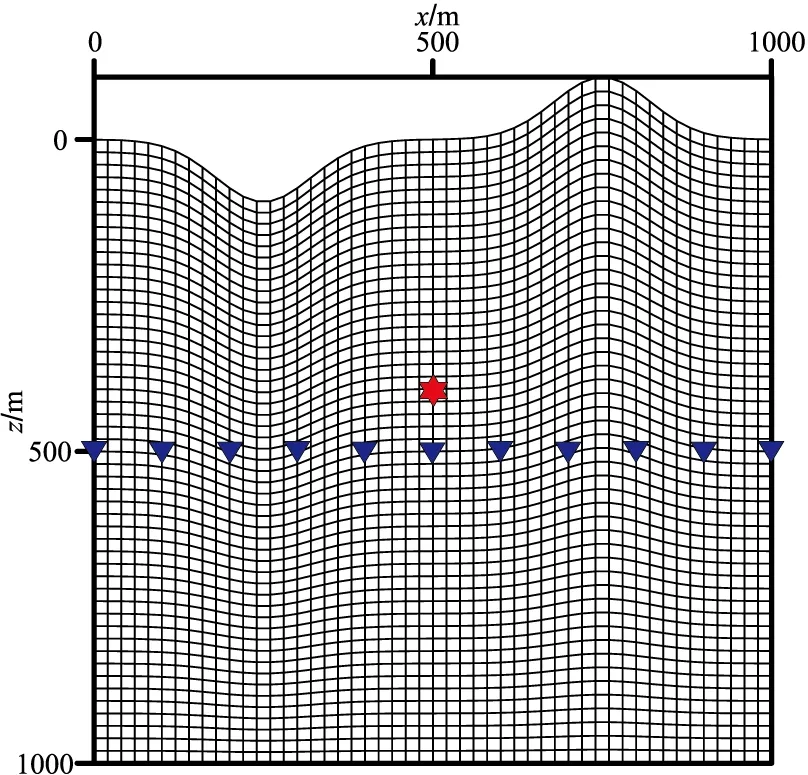
圖4 模型網格剖分示意圖紅星和藍三角分別為震源和檢波器

圖5、圖6、圖7分別為起伏地表聲波、彈性各向同性和彈性VTI-1均勻介質模型的2.5D數值解的vx和vz分量波場快照，從中可以清楚地看到直達P波及自由地表產生的反射波。圖8、圖9、圖10為三個起伏地表模型2.5D與2D數值解的波形對比，其中2D數值解是令式(50)中ky=0后采用本文相同方法獲得。2.5D數值解和2D數值解之間不僅存在著明顯的振幅差異，還存在相移。

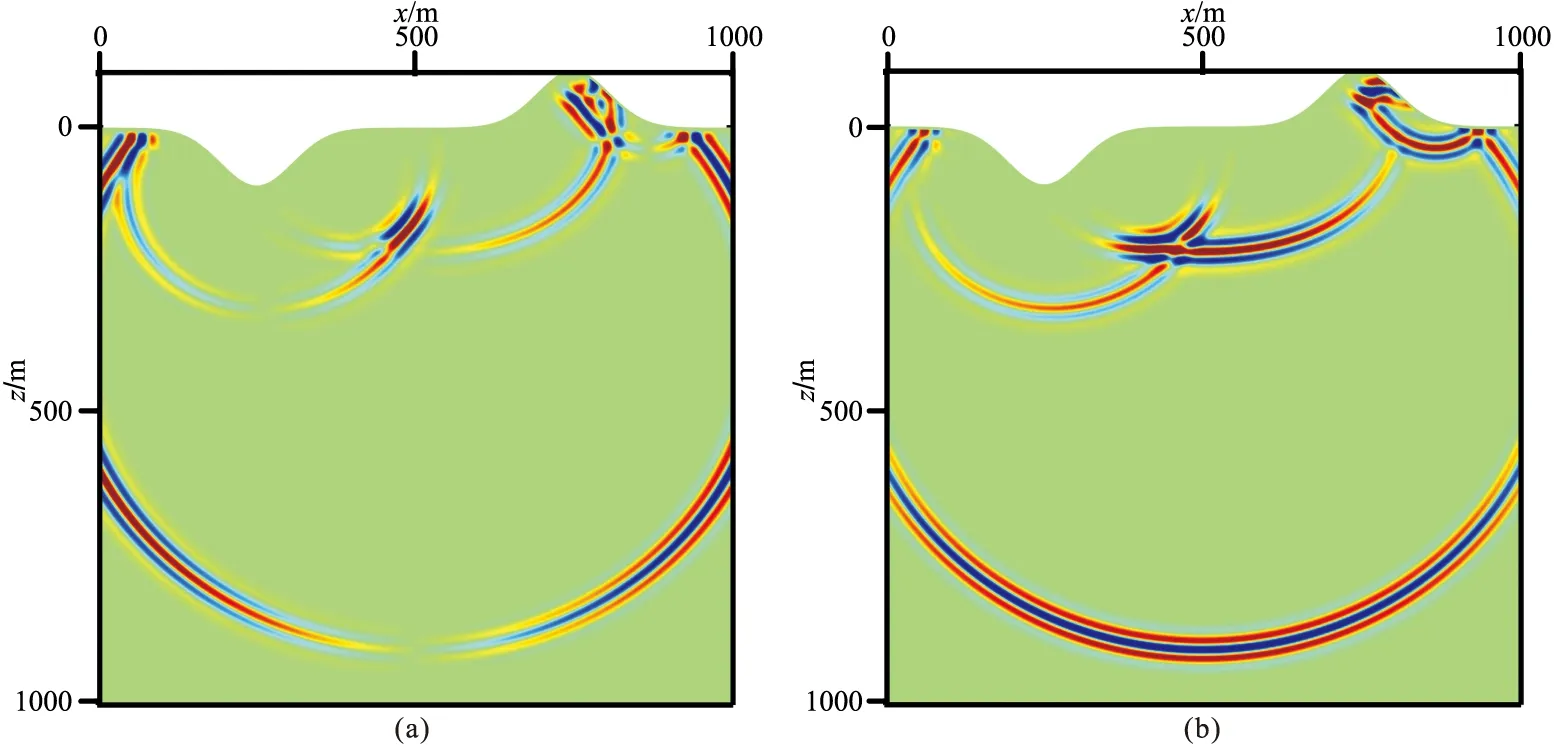
圖5 起伏地表聲波均勻介質模型2.5D數值解vx(a)和vz(b)分量在0.4s的波場快照

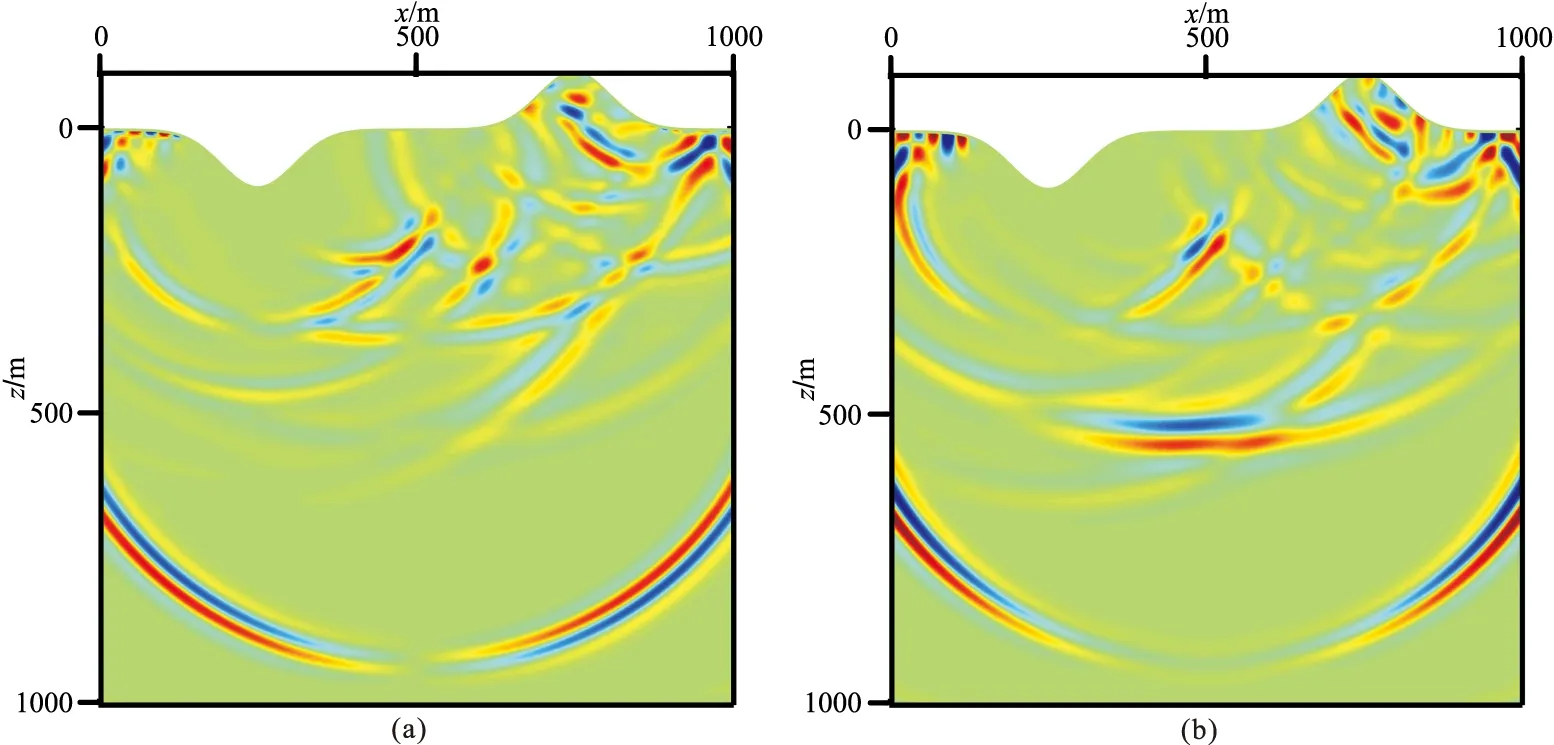
圖6 起伏地表各向同性均勻彈性介質模型2.5D數值解vx(a)和vz(b)分量在0.32s的波場快照

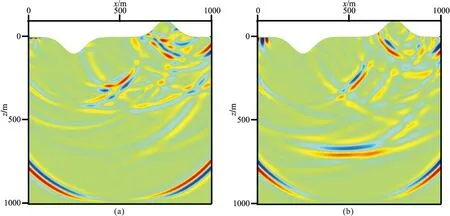
圖7 起伏地表均勻VTI-1介質模型2.5D數值解vx(a)和vz(b)分量在0.32s的波場快照

圖8 起伏地表聲波均勻介質模型2.5D與2D數值解對比(a)vx分量；(b)vz分量；(c)圖a的歸一化顯示；(d)圖b的歸一化顯示。下圖為上圖方框的放大顯示

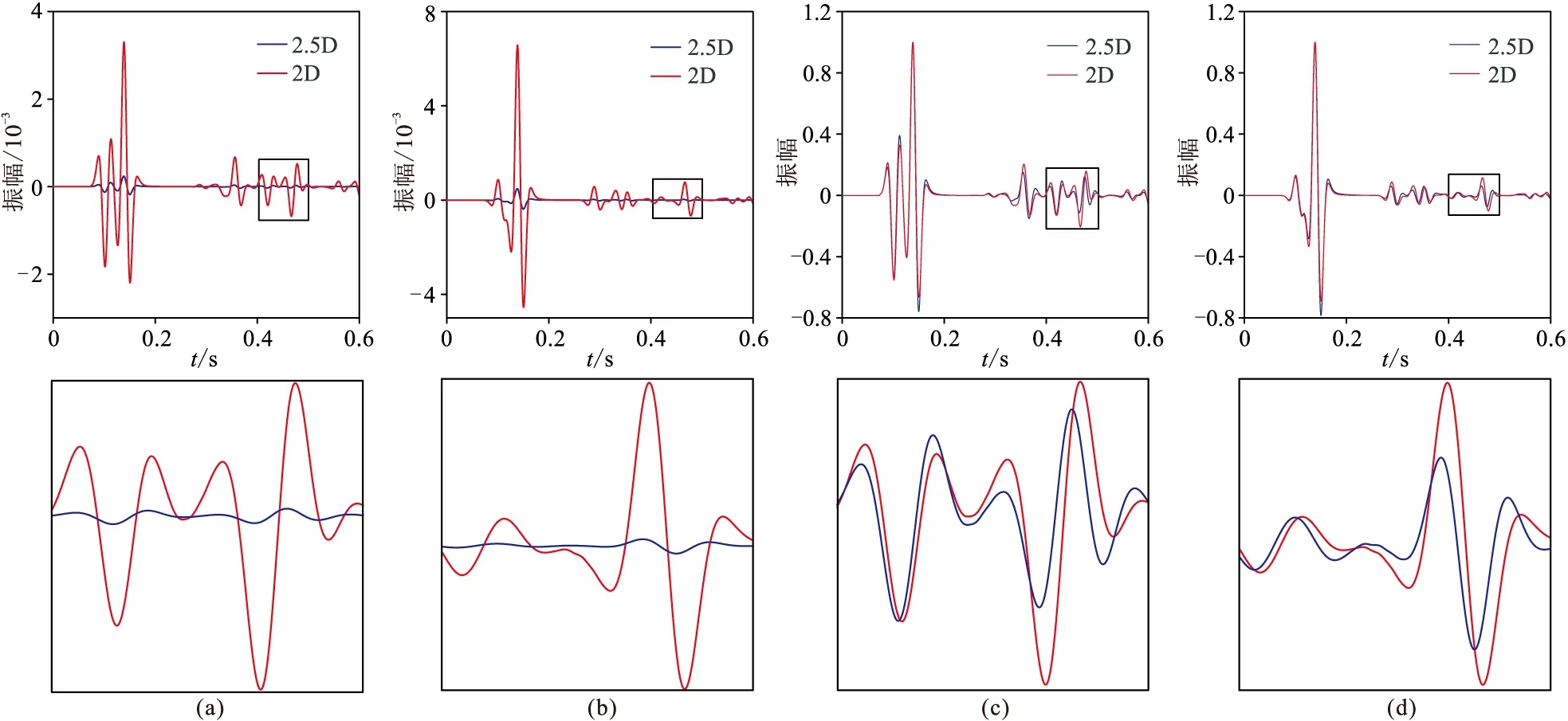
圖9 起伏地表均勻各向同性彈性介質模型2.5D與2D數值解的對比(a)vx分量；(b)vz分量；(c)圖a的歸一化顯示；(d)圖b的歸一化顯示。下圖為上圖方框的放大顯示

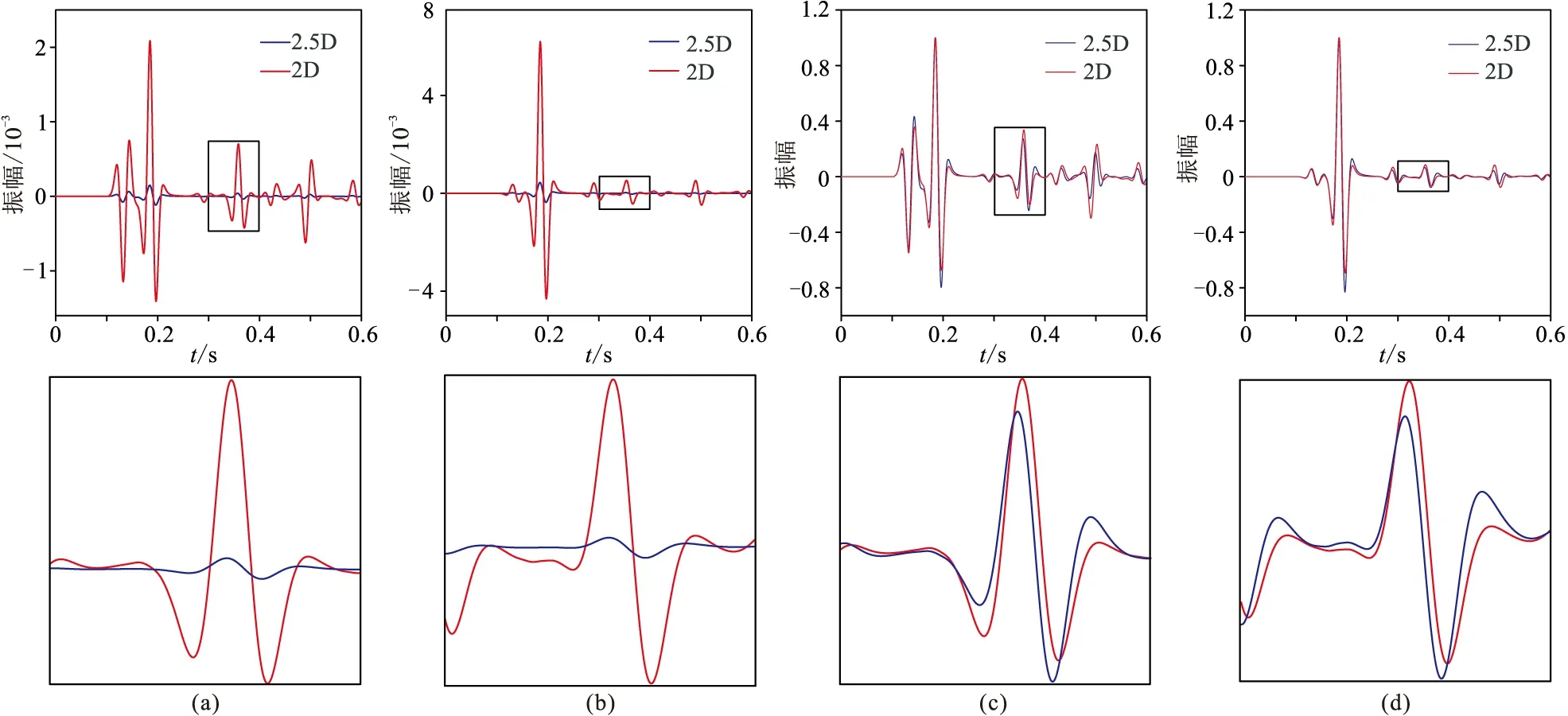
圖10 起伏地表均勻VTI-1介質模型2.5D與2D數值解的對比(a)vx分量；(b)vz分量；(c)圖a的歸一化顯示；(d)圖b的歸一化顯示。下圖為上圖方框的放大顯示

5.2 固—液耦合模型

建立一個正弦起伏固—液耦合界面模型(圖11)驗證本文的2.5D數值模擬方法適用性。模型尺寸為1000m×1000m，網格間距為2m，第一層為聲波介質，第二次為各向同性介質(參數見表1)。震源位于(500m，300m)，5個檢波器等間距布置于(300m，0m)與(300m，400m)之間。圖11為2.5D數值解的0.28s時刻波場照，從圖中可以觀察到直達P波經過固—液界面產生了清晰的透射P波和S波；圖12是2.5D與2D數值解的波形對比，可以看出2.5D與2D數值解之間同樣存在著明顯的振幅差異和相移現象。

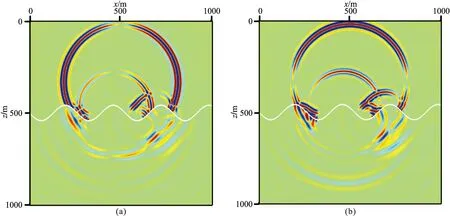
圖11 固—液耦合模型2.5D數值解vx(a)和vz(b)分量在0.28s的波場快照圖中起伏曲線為正弦起伏界面

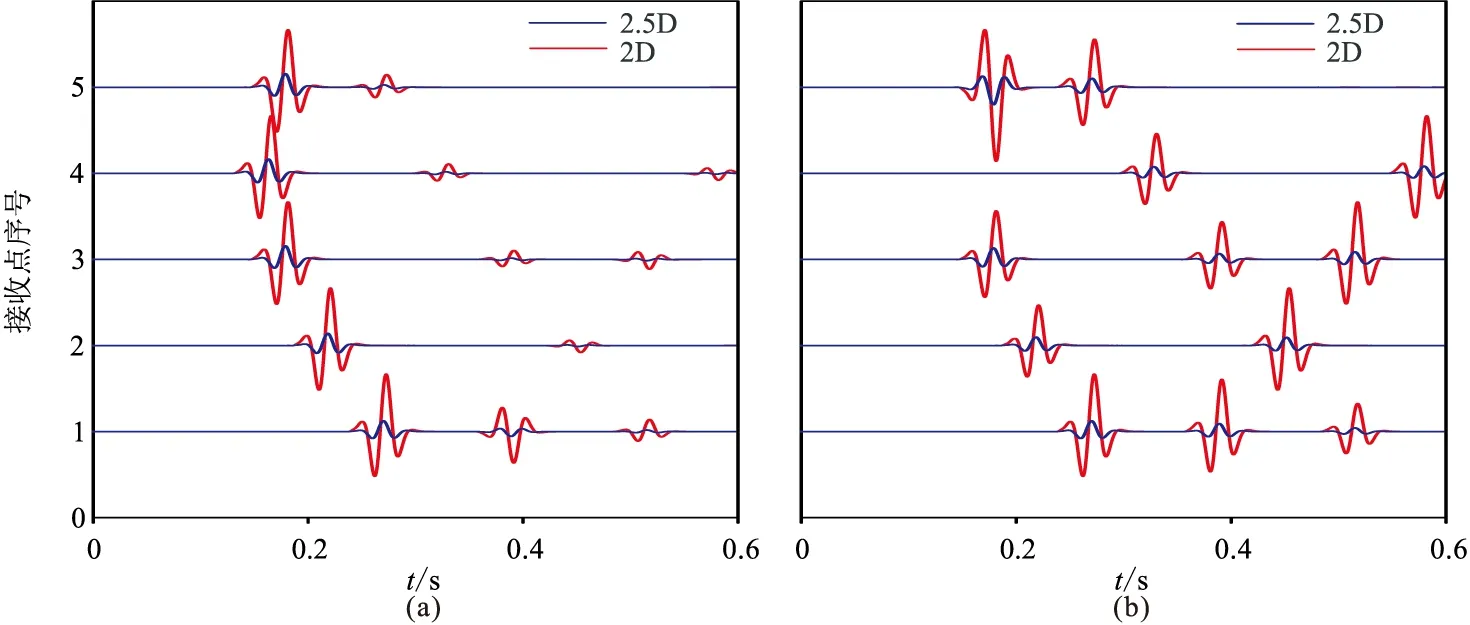
圖12 固—液耦合模型2.5D與2D數值解波形對比(a)vx分量；(b)vz分量

5.3 三層混合模型

為了檢驗本文2.5D波場數值模擬方法對于復雜介質的適用性，選擇一個三層模型(圖13)進行實驗。該模型第一層為聲波介質(水)，第二層為彈性各向同性介質，第三層為VTI彈性介質(VTI-2)，各層彈性參數見表1。震源位于(1000m，450m)；三個檢波器分別位于(500m，200m)、(500m，500m)、(500m，800m)，每層各有一個。圖14為三層模型2.5D數值解vx分量在不同時刻的波場快照，可以看出清晰的反射波、轉換波、透射波和多次波。由圖14a、圖14b可以看出，當P波和S波到達固—液邊界時，透射和轉換后的P波出現在第一層(聲波介質)中，而反射和轉換后的P波和SV波在第二層(各向同性介質)中向下傳播；在第三層(VTI-2介質)中出現P波和S波穿過固—固界面產生的透射和轉換波。由圖14c～圖14f可以發現，當波傳播到自由表面產生了反射的P波，在第二層介質中出現了清晰的多次波。圖15、圖16、圖17分別為三個檢波器的2.5D與2D模擬記錄對比，可以看出，無論檢波器位于何種介質中，二者存在明顯的振幅差異和相移。

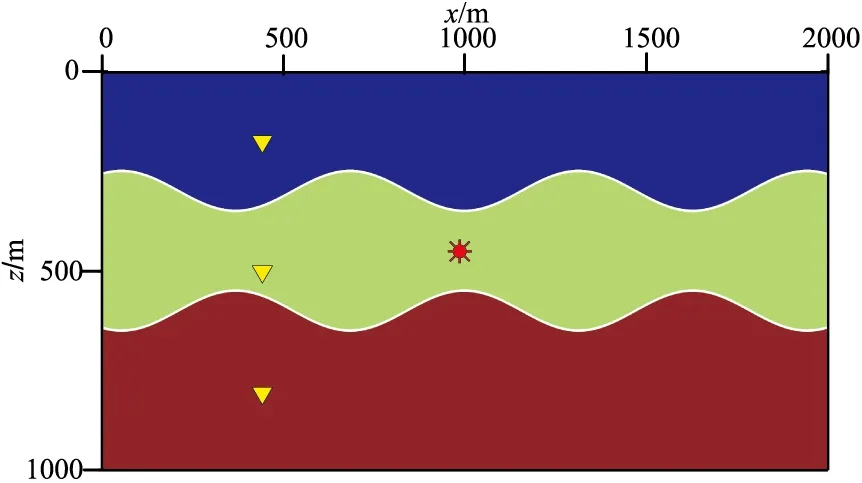
圖13 三層模型示意圖星和三角分別表示震源和接收器點位置

圖14 三層模型2.5D數值解vx分量在不同時刻的波場快照(a)0.12s；(b)0.20s；(c)0.28s；(d)0.36s；(e)0.44s；(f)0.52s

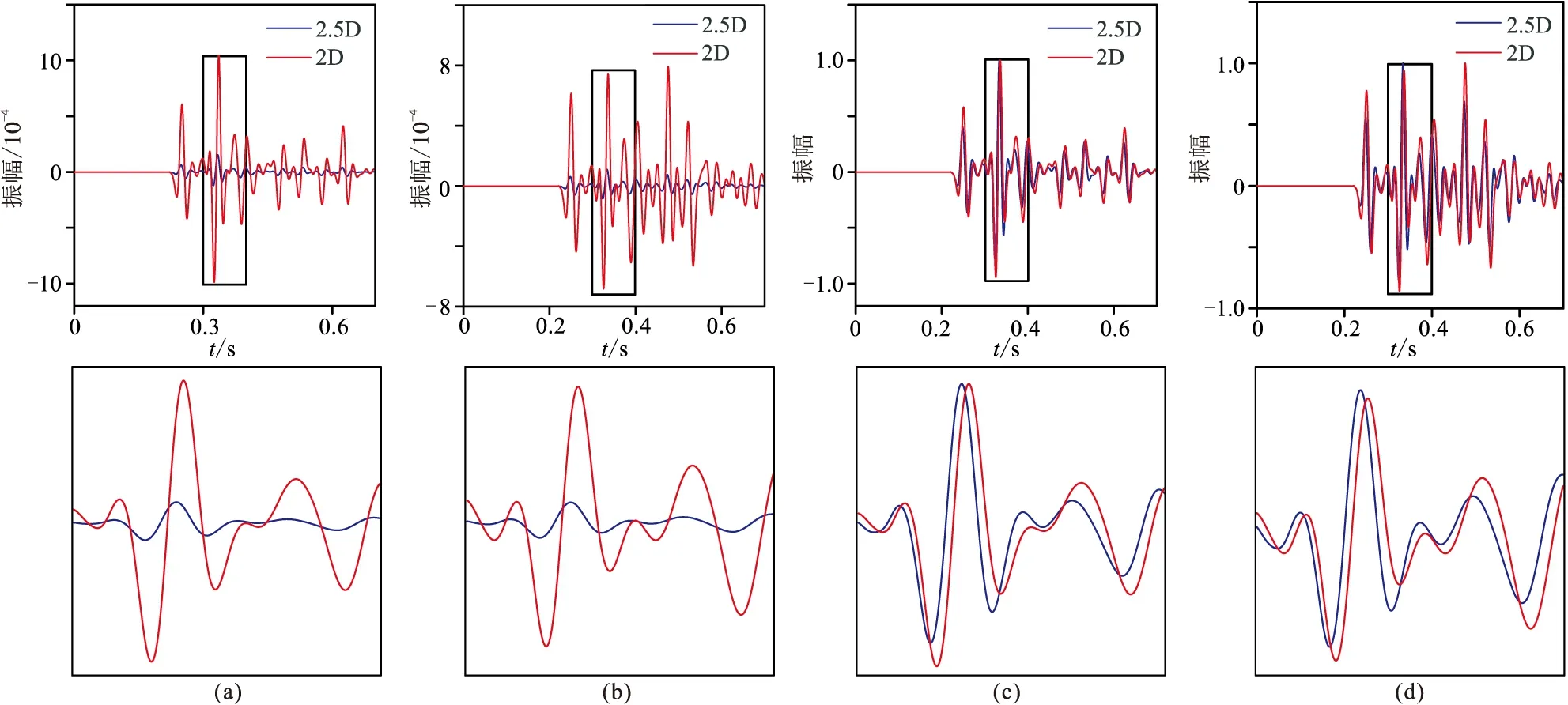
圖15 三層模型第一個檢波器的2.5D與2D數值模擬記錄對比(a)vx分量；(b)vz分量；(c)圖a的歸一化顯示；(d)圖b的歸一化顯示。下圖為上圖方框的放大顯示

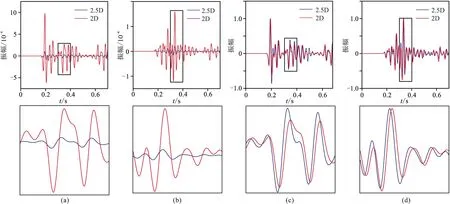
圖16 三層模型第二個檢波器的2.5D與2D數值模擬記錄對比(a)vx分量；(b)vz分量；(c)圖a的歸一化顯示；(d)圖b的歸一化顯示。下圖為上圖方框的放大顯示

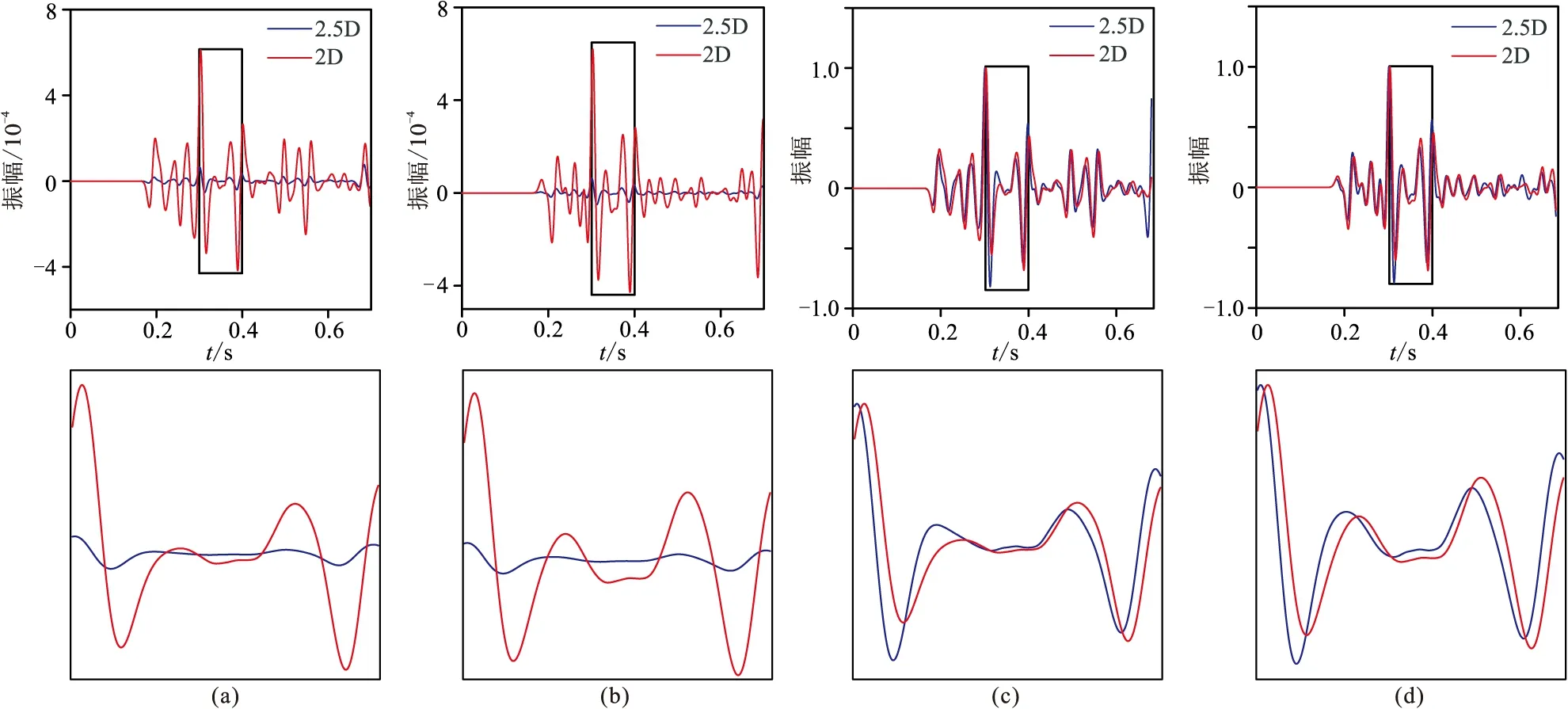
圖17 三層模型第三個檢波器的2.5D與2D數值模擬記錄對比(a)vx分量；(b)vz分量；(c)圖a的歸一化顯示；(d)圖b的歸一化顯示。下圖為上圖方框的放大顯示

三層混合模型模擬結果表明，本文方法適用于復雜介質2.5D地震波數值模擬。

6 結論

本文通過推導、整理得到了一個矩陣形式的2.5D廣義一階速度—應力波動方程，該方程不僅適用于聲波介質和一般各向異性介質，而且適用于不同的邊界條件(聲波自由地表、固體自由地表和固—液邊界條件)。通過定義不同的波場矢量，并根據模型離散點介質參數的變化給出了三個系數矩陣，在壓力或應力矢量上施加點源后采用數值方法求解，可以用一個計算機程序實現復雜介質中的2D或2.5D地震波場數值模擬。為了更好地貼合起伏地形，本文選擇曲線網格有限差分法求解波動方程，數值模擬實驗表明，在不同的介質中本文方法模擬得到的2.5D數值解與3D解析解非常匹配，并且適用于不同的邊界條件。除此之外，本文驗證了2.5D數值方法的計算效率遠優于3D數值方法。這種2.5D數值模擬方法可以直接用于實際點源地震數據的逆時偏移成像。

附錄A 彈性各向異性介質中波動方 程的系數矩陣

將式(3)、式(4)寫成矩陣形式，則式(6)中的系數矩陣可表示為

(A-1)

(A-2)

(A-3)

式中

(A-4)

(A-5)

(A-6)

(A-7)

(A-8)

(A-9)

(A-10)

(A-11)

(A-12)

(A-13)

(A-14)

附錄B 聲波介質中波動方程的系數 矩陣

將式(12)和式(13)寫成矩陣形式，則式(15)的系數矩陣為

(B-1)

(B-2)

(B-3)

附錄C 固體自由地表中波動方程的 系數矩陣

將式(31)和式(32)寫成矩陣形式，則式(34)系數矩陣可表示為

(C-1)

(C-2)

(C-3)

式中：

(C-4)

(C-5)

(C-6)

(C-7)

(C-8)

(C-9)

附錄D 固—液邊界中波動方程的系 數矩陣

將式(45)～式(47)聯合寫成一個矩陣形式，可導出式(49)的系數矩陣，為

(D-1)

(D-2)

(D-3)

式中：

(D-4)

(D-5)

(D-6)

(D-7)

(D-8)

(D-9)