低秩稀疏重建分析的邊緣檢測方法

劉 軍 宋維琪 陳俊安 譚 明 胡建林 董 林

(①中國石化西北油田分公司，新疆烏魯木齊 830011；②中國石油大學(華東)，山東青島 266580)

0 引言

碳酸鹽巖地區由于溶蝕作用，斷層往往伴有縫洞。研究斷層及其伴生的縫洞，對儲層預測具有重要意義。邊緣檢測方法眾多，如方差體方法、螞蟻追蹤方法[1]、曲率屬性方法及其他方法[2-4]、多代相干體算法[5-7]、Canny算子邊緣檢測方法、sobel算子邊緣檢測算法等，最新的方法有相似屬性方法、Likelihood屬性方法、混亂屬性相干方法等。其中相似屬性方法、Likelihood屬性方法及多代相干體方法實質上也是相干方法。上述方法是非常有效的斷層檢測方法，取得了很好的應用效果[8-14]，但也有其自身的不足和邊緣檢測能力的限制，特別是對噪聲干擾、多邊緣干涉及弱小目標邊緣的檢測效果不理想。曲率屬性方法、Canny算子和sobel算子邊緣檢測方法涉及梯度計算，嚴重放大了噪聲，檢測結果的可靠性差。

壓縮感知理論是近年來新的信號處理理論，在數據壓縮、傳輸領域得到廣泛應用。壓縮感知理論的稀疏重建理論[15-17]為信號重建提供了新的理論方法，在圖像重建領域普遍獲得較好效果[18-21]；在地震勘探領域，人們利用壓縮感知理論去噪[22]、數據重建[23]、拓頻處理，取得了較好效果。

針對邊緣檢測存在的問題，本文首先分析斷層邊緣和縫洞邊緣的空間分布特征，根據斷層邊緣和縫洞邊緣的地震響應特征，把低秩稀疏分析理論引入邊緣檢測，研究邊緣信息、背景信息及噪聲信息的低秩稀疏分解與重建；為了提高邊緣檢測能力和分辨率，在壓縮感知稀疏表示基礎上，對地震資料進行深度稀疏化表示，結合向量稀疏表示和矩陣稀疏表示，通過低秩稀疏分析理論[24-25]，形成一種全新的邊緣檢測方法。

1 基本框架理論

1.1 信號分析低秩表示模型

低秩表示思想是構建一個能夠表示所有樣本能力的字典，并且每個樣本都可以用字典中的原子線性表示，同類樣本的表示系數具有相關性，故整個表示系數矩陣是一個低秩矩陣。該模型可以更好地挖掘數據的結構信息，較好地解決多線性子空間聚類和分離問題。由于矩陣滿足低秩條件，所以可以保證同類數據樣本聚集到相同的子空間。

在復雜的地震資料邊緣檢測中，相似背景和稀疏目標組成了地震響應的所有成分，背景又由多種子背景構成。背景和局部目標也是相對的，若研究目標是斷層，則地層相對于斷層為背景；若研究目標是斷層中的縫洞，則斷層相對于縫洞為背景。

1.2 低秩稀疏表示

根據低秩稀疏分解理論，假設地震信號S由區域相似信息和局部信息構成，則可以分解為低秩矩陣B和稀疏矩陣D兩部分，即：S=B+D，其中B為背景部分(低秩部分或相似部分)，D為高秩部分(稀疏部分)。可利用信息主成分分析求解最優低秩矩陣B，即求解下列優化問題

minB,D‖S‖F滿足 rank(B)≤r,S=B+D

(1)

式中：r為矩陣的秩；‖S‖F為Frobenius范數。

通過此約束問題，可以找到矩陣S在一個R維線性子空間的投影。當矩陣D的元素服從獨立高斯分布時，對S進行奇異值分解，便可得到式(1)的最優解。如果D不滿足以上條件，式(1)無解或誤差較大。于是利用穩健的主成分分析方法解決這個問題。引入正則化參數μ，得到新的優化問題

min [rank(B)+μ‖D‖F]滿足S=B+D

(2)

上述優化問題是一個NP-hard問題，因此對目標函數進行松弛，即將非凸函數問題轉化為凸函數問題，利用核范數代替矩陣的秩，如L1范數代替L0范數。此時的凸優化問題為

min[‖B‖1+μ‖D‖1]滿足S=B+D

(3)

利用壓縮感知理論，將式(3)改為

min‖S-A(B+D)‖F滿足‖B‖2≤r,‖D‖0≤k

(4)

式中：A為字典矩陣；k為稀疏目標的稀疏度，取決于稀疏目標的大小和數目，而低秩化程度估計的準確度直接影響背景的抑制效果。由式(4)可知，模型在矩陣的秩和向量的稀疏度約束下求目標函數的最優解。通過求解以上最優問題，使背景相似信息和局部稀疏信息最佳分離，有效分離地質體邊緣信息、地層信息及噪聲，從而進行邊緣檢測。

1.3 向量信號稀疏與矩陣低秩稀疏特征分析

信號的稀疏分解可以是一維向量，如一維小波分解，也可以是二維矩陣，如曲波分解。矩陣的秩刻畫了矩陣不相關行或列的數目，一個矩陣中的不相關的行或列越少，則該矩陣的秩越小，反之亦然。矩陣奇異值分解能夠提取高維數據的局部特征及約減維數，其本質是將分類能力弱的數據集合(矩陣)的類間方差增大，提高分類能力。矩陣的奇異值個數越少，奇異值分解越稀疏，因此稀疏和低秩是一致的，反映數據的壓縮能力。

2 地震資料低秩稀疏邊緣檢測方法

基于壓縮感知原理和假設，可以將邊緣檢測問題轉化為壓縮與矩陣的低秩稀疏分解問題。通過低秩稀疏分解方法壓制地層信息，從而分離邊緣信息。通過數據的矩陣結構變換，把地層信息變換為低秩部分，把邊緣信息變換為稀疏部分，利用奇異值分解壓制地層信息進而分離邊緣信息。信號重建的可靠性、精度及分辨率都和信號的稀疏化分解程度有關。由低秩稀疏分解理論[24-25]可知，要得到唯一的分解結果，要求稀疏部分獨立和高度稀疏。實際地震記錄的邊緣信息、地層信息及噪聲等遠不能滿足高度稀疏與獨立的條件。

2.1 地震信號向量稀疏表示及去噪優化

地震資料稀疏表示是提高邊緣檢測能力的關鍵環節之一。利用壓縮感知理論對地震信號向量稀疏表示，采用平穩小波分解方法對地震信號進行多尺度小波分解，建立小波稀疏表示字典。有效信號壓縮重建就是稀疏系數優化和稀疏系數加權組合的過程。含噪信號通過某種基分解，使信號和噪聲的特征不同而分離。通常情況下，噪聲系數呈均勻分布，信號系數呈冪律分布。對于能量較大信號，稀疏分解使有效信號的能量強于噪聲，可根據壓縮感知理論的優化方法壓制噪聲；對于能量較小信號，稀疏分解使有效信號與噪聲能量水平相當，此時壓縮感知理論優化方法對噪聲的壓制效果不理想。假設在橫向上信號稀疏分解后有效信號系數相關，而噪聲系數不相關，則可采用橫向相關法對稀疏系數去噪處理。

2.2 矩陣低秩稀疏表示及優化方法

以上分析了信號在某種正交基下的稀疏表示方法。為了充分挖掘數據結構方面的信息，以下從矩陣秩角度討論稀疏化問題。

2.2.1 張量奇異值分解

矩陣稀疏分解有很多方式，為了更好地分析低秩問題，本文采用奇異值分解稀疏表示方法。數據矩陣的秩既與數據本身尺度有關，還與數據的排列方式(數據結構)有關。地質體是三維的，地質體地震響應信息也是三維的，把三維數據分解成二維矩陣進行奇異值稀疏分解，涉及張量分析及高階奇異值分解。一般奇異值分解針對2階張量矩陣，對于高階張量，奇異值分解是高階奇異值分解。高階奇異值分解難以分析其低秩稀疏特征，為了研究簡便，這里采用張量分解的方法，即把一個子數據體塊分解成一系列二維矩陣，對于不同的分解模型，通過分析每個矩陣的低秩稀疏特征，構建具有最優低秩稀疏結構信息的張量分解模型。

2.2.2 矩陣低秩優化

(1)矩陣張量構建與優化

對于一個數據集合，不同矩陣組建方式有不同的矩陣分解特征，從而有不同的信息表示能力。根據多線性代數理論，張量是一個N維數組，則張量的階數也為N。向量是一階張量，矩陣是2階張量，立體矩陣是3階張量。數據信息包括能量信息、結構信息等。立體矩陣包含了全面的結構信息，為了充分挖掘結構信息，對三維地震數據進行立體矩陣分析建模。將子塊三維數據分解成二維矩陣的模式很多，如果把所有分解模式都列出計算，計算量太大而不適合于實際分析。在斷層和縫洞檢測中，斷層在二維情況下具有線狀特征，洞邊緣在二維情況下具有等軸(近似圓)特性。根據檢測的兩類邊緣信息，分別構建行、列數不同的矩陣和行、列數相同的矩陣。對于斷層檢測問題，在縱向構建非方陣，即線、道及45°線方向共四個二維矩陣，在橫向構建方陣，即過計算點的一個方陣；對于縫洞檢測問題，在縱、橫向均構建方陣。

(2)奇異值分解去噪優化

矩陣低秩優化包括矩陣建模和奇異值分解去噪，以下討論矩陣去噪優化。矩陣低秩優化就是通過某種方式盡可能獲得具有最小秩的表示矩陣，也就是尋找一個最佳的低秩表示，達到矩陣低秩稀疏優化的目的，從而提高算法的準確性和邊緣檢測的分辨率。無論采用何種矩陣建模，都不能直接消除數據集合中噪聲的影響。矩陣分析理論表明，矩陣中個別元素的突變會使矩陣的數目和大小發生明顯變化，這種變化與該元素和矩陣的方差呈線性關系。矩陣奇異值分解去噪低秩優化問題就是使矩陣秩最小化問題。

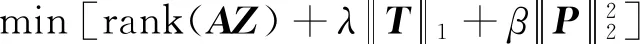
S=AZ+T+P

(5)

式中：B=AZ是分解字典矩陣，Z是系數矩陣；T為稀疏目標；P為噪聲；λ、β為兩個待定參數。

將式(5)寫為

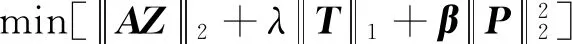
S=AZ+T+P

(6)

通過增廣拉格朗日乘子方法，將式(6)的約束優化問題轉化為一個無約束優化問題，優化目標函數為

(7)

式中：等式右邊第1項代表奇異值分解；第2項代表壓縮感知稀疏分解重建；第3項代表噪聲，主要為奇異值分解的噪聲，壓縮感知的噪聲已去除；第4項和第5項為信號自身的約束，γ、ρ為懲罰參數。后三項都是2范數，以保證計算過程既要壓制噪聲，又要保證新的重建信號是期望信號(去除噪聲的原始信號)。式(7)綜合了小波向量稀疏優化、矩陣稀疏優化及各種約束問題，利用現有的固定變量迭代方法求解，根據研究問題的特點和算法實現要求，采用閾值迭代方法進行優化。

3 算法實現步驟

由稀疏分解、稀疏系數去噪優化及矩陣建模等一系列方法得到多尺度的優化小波系數，并進行張量矩陣建模。對張量建模分解矩陣進行奇異值分解，再對矩陣奇異值進行低秩優化，根據優化后的奇異值結果重建邊緣信息。具體算法步驟如下。

(1)地震資料平穩小波分解。利用平穩小波變換方法對地震資料進行多尺度小波分解，得到地震資料的小波稀疏字典。

(2)多尺度小波系數優化。為了最大程度地壓制噪聲，利用有效信號和噪聲的分解系數分布特征，利用壓縮感知中的MP算法和系數特征擬合方法，優選最優小波系數去噪；利用優選的分解系數通過橫向相鄰點進行相關計算，再次選出相關系數大的小波系數。

(3)根據多尺度優化小波系數建立張量矩陣并進行建模。通過張量建模，構建地震數據邊緣信息分類最優的矩陣表示模式。

(4)張量矩陣奇異值分解。對三維地震數據子塊(立體矩陣)進行二維矩陣分解，并對各個分解矩陣進行奇異值分解。

(5)矩陣奇異值低秩優化。根據目標函數(式(7))，采用閾值迭代方法優化計算，以提高矩陣的低秩稀疏優化程度，從而壓制奇異值分解噪聲。

(6)雙稀疏和雙優化結果融合與重建。將小波分解稀疏、矩陣奇異值分解稀疏和小波系數優化、矩陣低秩稀疏優化結果進行雙稀疏、雙優化與重建。

4 模型分析

為了測試、分析低秩稀疏邊緣檢測方法(下文簡稱本文方法)對邊緣信息的識別能力及方法適應性，分別對小斷層理論模型和實際模型進行測試、分析。圖1為小斷層反射系數模型及其邊緣檢測結果。由圖可見，本文方法(圖1e、圖1f)清晰地識別了三條小斷層，對小斷層的識別效果明顯好于相干方法(圖1c、圖1d)，其中對主頻為20Hz雷克子波合成的含噪記錄(圖中沒有展示)的相干檢測結果(圖1d)中沒有斷層顯示。上述結果說明本文方法的抗噪性較強。

圖1 小斷層反射系數模型及其邊緣檢測結果(a)小斷層反射系數模型；(b)主頻為25Hz雷克子波與圖a褶積形成的含噪記錄；(c)相干(25Hz)；(d)相干(20Hz)；(e)本文方法(25Hz)；(f)本文方法(20Hz)。模型中存在三條小斷層，斷距分別為3個采樣點(30m)、2個采樣點(20m)和1和個采樣點(10m)

圖2為實際斷層模型及其邊緣檢測結果。由圖可見，本文方法很好地指示了常規斷層(圖2c)，同時在斷層模型剖面(圖2a)上未能指示應出現斷層的部位，相干結果較模糊、散亂(圖2b)，但本文方法較清晰地揭示了斷層并且斷層連續性好(圖2c)。上述結果說明本文方法的適用性較強。

圖2 實際斷層模型及其邊緣檢測結果(a)斷層模型剖面；(b)相干方法；(c)本文方法

5 實際資料應用效果分析

利用實際資料驗證本文方法的應用效果。圖3為不同規模矩陣的直接奇異值檢測結果。由圖可見：7×5階矩陣(橫向的窗口尺度大于縱向)檢測結果對地層邊緣壓制效果差(圖3b)；5×17階矩陣檢測結果清楚顯示了斷層，地層壓制效果較好(圖3c)。因此，對于同樣的方法，不同規模矩陣的直接奇異值檢測結果不同。矩陣行、列元素(橫、縱向窗口的尺度)的關系體現了低秩化揭示橫、縱向方向特性結構信息的能力，同時說明矩陣建模對于揭示結構信息的重要性。上述分析表明，直接對地震信號進行奇異值分解，只能揭示較大的斷層，不能揭示小斷層，并且檢測結果模糊、不清晰。

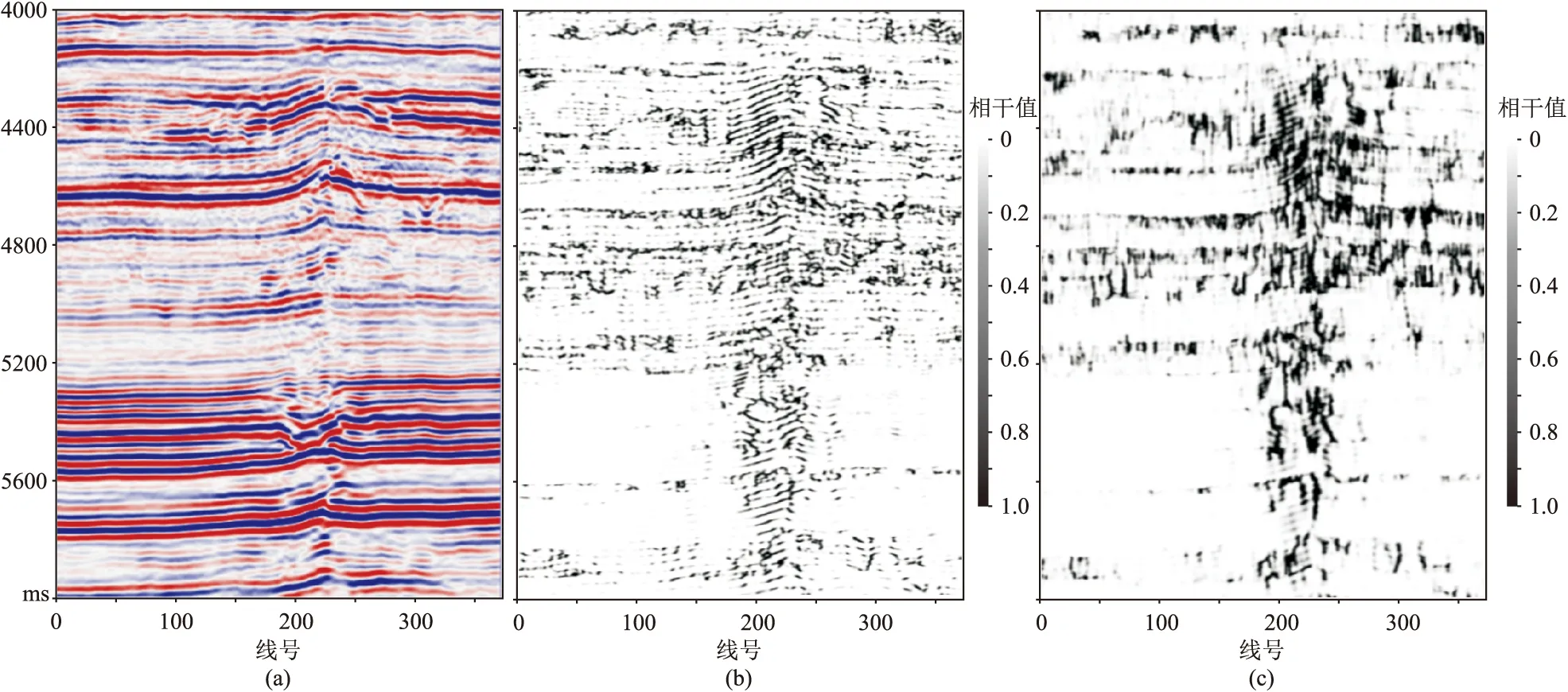
圖3 不同規模矩陣直接奇異值檢測結果(a)地震剖面；(b)7×5階；(c)5×17階

圖4為不同尺度組合雙稀疏邊緣檢測結果，其計算過程是對地震信號進行小波稀疏分解后再進行奇異值分解，在計算過程中對地震信號進行5級分解，通過把多尺度信息與雙稀疏(小波分解與矩陣分解)分析融合到算法實現，極大地提高了斷層尤其是小斷層的檢測能力。由圖4可見：①信號向量的稀疏分解稀疏度越大，奇異值分解低秩度也越大，即實際檢測結果分辨率提高，地層信息得到壓制。②在高頻邊緣信息具有完備性，低頻邊緣信息具有冗余性；向量稀疏促進了矩陣低秩稀疏，再次說明雙稀疏對提高邊緣檢測能力的意義。

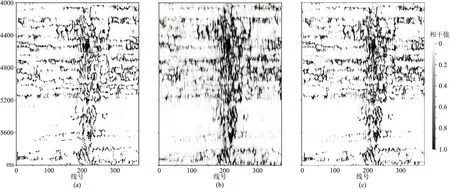
圖4 不同尺度組合雙稀疏邊緣檢測結果(a)第2尺度；(b)第2、第3尺度組合；(c)所有尺度組合

相似背景組成的矩陣具有低秩特征，突變信號與噪聲具有稀疏特征。如果相似背景有噪聲干擾，則背景的低秩化程度大大降低，背景越“干凈”其組成的矩陣相似性越高，矩陣低秩化程度越大，稀疏化程度也越大。“干凈”背景下存在斷層或縫洞等邊緣信息時，分離效果最好。本文的研究主旨是通過稀疏分解壓制噪聲、增強稀疏化、最佳低秩化，從而最大程度地分離背景信息和邊緣信息，增強邊緣檢測能力。

圖5為優化前、后邊緣檢測結果。由圖可見，聯合優化結果明顯、清晰，極大地壓制了噪聲(圖5b)。圖6為本文方法與相干法邊緣檢測結果對比。由圖可見，在小斷層檢測能力、分辨率及斷層的連續性方面，本文方法的邊緣檢測效果都明顯優于相干方法。圖7為洞邊緣層切片，由圖可見，與相干法洞邊緣層切片(圖7b)相比，本文方法洞邊緣層切片(圖7c)對洞邊緣的識別效果更好。

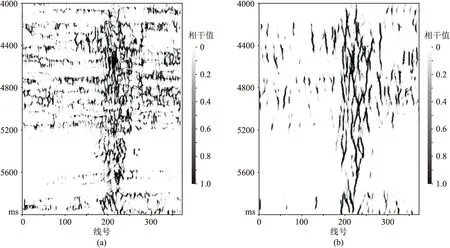
圖5 優化前(a)、后(b)邊緣檢測結果

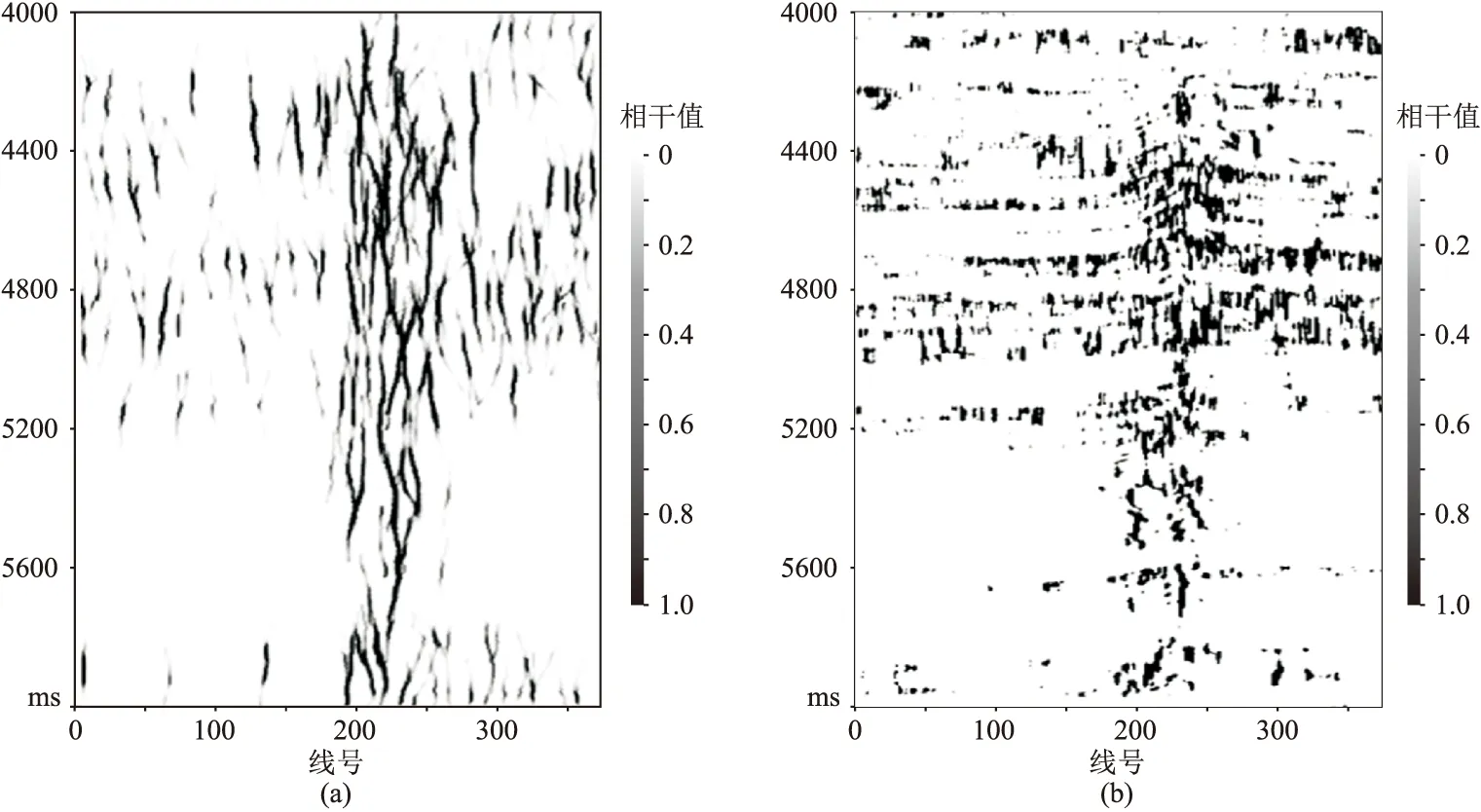
圖6 本文方法(a)與相干法(b)邊緣檢測結果

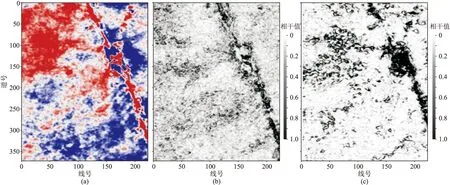
圖7 洞邊緣層切片(a)原始切片；(b)相干方法；(c)本文方法

6 結束語

斷層和縫洞邊緣檢測實質上是利用地震資料壓制地層信息和噪聲、突出邊緣信息的過程。地層信息具有低秩特性，噪聲和邊緣信息具有稀疏特性。提高邊緣檢測與識別能力，就是提高邊緣信息的類間分類能力和噪聲壓制能力。根據噪聲和有效信號的稀疏域分布特征，利用冪律特征約束，通過擬合方法對能量相近的噪聲和有效信號系數再次優化。為了挖掘數據結構信息，提高邊緣檢測能力，圍繞相似背景目標和稀疏目標分離，利用張量矩陣建模和奇異值分解方法，通過雙稀疏和雙優化，即小波分解稀疏、矩陣分解稀疏和小波系數優化、矩陣低秩優化，增強了尺度分析的正交性和類間分類能力，提高了重建結果分辨率和精度。與相干方法相比，本文方法對于斷層和縫洞邊緣具有更好的刻畫能力，較全面地揭示了較小的縫洞和小斷層信息。