基于改進的層次分析法和模糊綜合評價法的灌區農業水權分配

高娟娟，賀華翔，趙嵩林，謝紀強

（1.中國水利水電科學研究院，北京100038；2.河南省安陽水文水資源勘測局，河南安陽455000）

0 引言

在中國，農業不僅是國家穩定的基礎，也是經濟社會發展的前提。然而，由于農業灌溉節水技術相對落后和水利配套設施覆蓋率低，導致典型的農業用水效率低的問題。且不斷增長的生態、生活、工業用水擠占農業用水，用水需求與可利用水資源量嚴重不匹配。因此，開展有關灌區農業水權分配、灌區水資源管理的研究以緩解當前灌區的缺水問題就顯得尤為重要。灌區農業水權分配是完善農業水權制度、夯實農業水價改革和建立水權市場的重要基礎。通過適當引水和配水以及改進田間灌溉設施，實現水資源的有效利用、促進農業發展、保障糧食安全。

在過去的30年中，國內外專家學者對初始水權分配問題進行了大量的研究。早期的研究包括John[1]和Zhong Jing W[2]從公平性和可持續性視角分配初始水權。根據土地面積、資金投入、公法、用水優先序、用水許可和合理收取水費分配初始水權[3-6]，彌補了原有灌區管理和取水許可制度的不足。隨著研究的深入，還開展了一些有關初始水權分配技術的研究，Zhang L N[7]在考慮條件風險值理論和基尼系數約束的基礎上，建立了水權分配的兩階段隨機規劃模型，通過優化水權分配方案，降低了局部水資源短缺的不公平風險。Wang H L[8]運用層次分析法建立行業水權分配的層次結構模型，并對行業水權分配進行了研究。胡潔[9]利用多層次多目標模糊優選方法對流域初始水權進行分配，分配結果較其他分配模式更具公平性、高效性及合理性。孫建光和顧沁揚等[10,11]對農業水權分配方法和分配制度進行了研究，為緩解農業用水矛盾提供了有效方案。管新建[12]應用基尼系數法分配灌區農戶間水權，為灌區水權分配提供了新思路。姚明磊和董斌[13]針對不同用水部門間日益激烈的用水矛盾，建立多目標規劃模型，將縣域水權合理分配至各用水部門。劉子豪等[14]通過驅動力-狀態-響應(DSR)框架對46 分水權制度進行分析，認為農業水權制度的完善和政策響應相互影響。

然而，以上初始水權分配方法各有利弊。非技術類方法因面積、土地、政策等因素的變化實時性較差；技術類方法包括最初的層次分析法、遺傳算法和兩階段隨機規劃等方法基本能夠解決多目標多層次的水權分配問題。但是，隨著相關研究的深入，該類方法的不足在于水權分配過程中受主觀性影響較大導致結果差異大。且鮮有將此類方法應用于灌區農業水權分配研究中，本文以灌區各支渠間水權分配為研究對象，采用改進的層次分析法和模糊綜合評價法作為技術支撐，通過構建灌區農業水權分配層次結構圖，對每一層指標進行標度賦值，確定評價指標優先序等級，引入模糊綜合評價法，建立模糊綜合矩陣，進行一致性檢驗，最終得到灌區各支渠間農業水權分配結果。提出一種在灌區現狀約束條件下使經濟效益達到最優的灌區各支渠間水權分配方法。

1 基于改進的層次分析法的灌區農業水權分配模型的構建

20世紀70年代，層次分析法（AHP）的概念最初被T L Saaty[15,16]提出，AHP的最大優點在于它能夠處理復雜的實際問題，并且易于操作。經過不斷改進[17,18]，已有研究表明，因層次分析法具有獨特性和優越性而被廣泛應用于地理信息系統[19,20]、生態脆弱性評價[21]、灌溉水質指標評價和灌溉工程應用[22,23]、灌區農業用水管理評價[24]等領域。層次分析法也被廣泛應用于解決水權分配中多層次、多目標的復雜問題[25]。然而，針對已有層次分析法解決初始水權分配過程中存在的欠缺與局限性，仍有很大的改進空間。本文針對灌區現狀水權分配模式未能綜合考慮各支渠基礎條件、經濟效益和生態環境等因素，提出采用改進的層次分析法和模糊綜合評價法解決灌區內工程、社會、經濟和生態準則中定性指標的模糊性。一般情況下斗農毛地理位置相距較近，基礎條件等亦相差不大，對其進行農業水權分配意義不大，故本文僅對和平灌區支渠間農業水權進行分配，在灌區現狀約束條件下探尋經濟效益最優的分配方法。

1.1 構建灌區農業水權分配層次結構圖

德爾菲法是在20世紀50年代發展起來的一種廣泛用于幫助預測各種學科決策的方法。本研究采用德爾菲法（Delphi method）[26]結合專家經驗對調查結果進行分析，構建一套結構強、代表性高、實用性強的灌區農業水權分配體系，由目標層、準則層、評判層和指標層組成的灌區農業水權分配層次結構圖，見圖1。層次劃分為4 類二級指標、12 類三級指標和17類四級指標。

1.2 改進的層次分析法

1.2.1 標度的轉換

原層次分析法構造判斷矩陣過程中以“1-9”的標度賦值較粗糙，有可能出現與實際情況相反的逆序，且矩陣一致性與思維一致性相脫節，不能準確量化每一層不同指標的隸屬度關系。經過大量研究理論知識及實踐經驗認為采取指數標度進行分析精度較高。一，指數標度以心理學中的韋伯-費希納定律[16]為基礎，使判斷思維與客觀判斷具有高度一致性；二，指數標度排序權值較為精細，縮小了人們的判斷差值；三，指數標度允許有多種形式。因此，指數標度具有的優異性能可以克服“1-9”標度存在的問題。標度之間的轉化，見表1。

1.2.2 判斷矩陣的建立及一致性檢驗

（1）判斷矩陣的建立。對每一層指標進行兩兩比較，根據兩個指標相對重要性進行標度賦值，并進行標度轉換得到eij值(表1)。構建判斷矩陣E=(eij)n×n。

表1 指標標度轉換Tab.1 Evaluation index scale conversion

計算判斷矩陣的特征向量[28]。公式如下：

式中：Gi為判斷矩陣E的每一行元素的乘積，i=1，2，3，…，n；Pi為Gi的k次方根值，k為判斷矩陣E的階數；Wi為判斷矩陣E的特征向量。

計算判斷矩陣E的最大特征值，計算公式如下：

式中：(EW)i為判斷矩陣E=(eij)n×n與特征向量Wi的乘積；λmax為判斷矩陣E的最大特征值。

（2）判斷矩陣的一致性檢驗。本研究通過建立模糊一致性矩陣對判斷矩陣進行深入檢驗。對判斷矩陣E=(eij)n×n的每一行進行求和，記為（其中i=1，2，…，n），uij=得到與判斷矩陣E相應的模糊一致性矩陣U=(uij)n×n。對于矩陣E和矩陣U，有如下兩個檢驗指標：

當α<0.2，且β<0.1 時，認為模糊互補矩陣較為符合現實，可繼續進行下一步計算；當α>0.2，或β>0.1 時，認為模糊互補矩陣不符合實際，需要專家進行重新判斷打分，并按步驟重新計算，直至符合條件為止。

1.3 灌區農業水權分配相關權重系數確定

(1)在確定準則層、評判層、指標層中各元素相對權重及優先序等級后，對指標層中各個指標的綜合權重系數進行計算：

式中：Fh為指標層中，第h個評價指標的綜合權重系數(h=1，2，…，17)；Bp為準則層中，第p類準則的權重系數(p=1，2，3，4)；Cq為評判層中，第q個評判指標的權重系數(q=1，2，3，…，12)；Dh為指標層中，第h個評價指標相對權重系數。

(2)對灌區中各支渠賦予0～1 之間的數值進行隸屬度分級，根據各支渠所屬隸屬度等級，結合指標層中各評價指標綜合權重系數，最終得灌區內各支渠農業水權分配總權重系數。計算公式如下：

式中：Ql為灌區中第l條支渠的總權重系數(l=1，2，…，16)；gl為第l條支渠的隸屬度。

2 模糊綜合評價法

本研究采用模糊綜合評價法將灌區農業水權分配過程中不可定量描述的指標進行定量處理。對復雜系統進行優選，對隸屬度函數進行模糊化處理，以解決評價等級在區間端點處數值小幅度變化時產生的跳級問題。計算得隸屬度矩陣R和模糊綜合矩陣B。令為第t個等級的隸屬度（等級劃分見表3），rh為評價指標的實際值，為第t個評價等級的上限，為第t個評價等級的下限，為第t個評價等級的均值。

(1)對于越大越好指標。

其他等級隸屬度為0；

其他等級隸屬度為0；

其他等級隸屬度為0；

(2)對于越小越好指標

其他等級隸屬度為0；

其他等級隸屬度為0；

其他等級隸屬度為0；

根據以上公式（10）～（19）計算得到每一層指標的隸屬度矩陣R，

結合改進的層次分析法和模糊綜合評價法將每一層指標的權重矩陣進行模糊變換，可得模糊綜合矩陣B。

式中：W為與公式（5）中特征向量Wi對應的矩陣。

3 實例研究

3.1 研究區概況

和平灌區位于慶安縣中部，呼蘭河左岸的干支流河漫灘及一級階地上。灌區內共有25個行政村，283個自然屯，總人口5.6 萬人。灌區內共有3 座渠首，干渠1 條，長45 km，支渠16 條和11 條直屬斗渠及3 處揚水站支渠，總長61.33 km，排水干渠15 條，總長51.2 km。灌區工程配套后，采用節水灌溉方法和節水工程技術，渠系水有效利用系數由改造前的0.5 提高到0.62。

3.2 和平灌區可分配水權總量

按照縣域內農業可分配水量核定情況，2016年和平灌區實灌面積6 666.67 hm2，有效灌溉面積4 866.67 hm2，分配水量為4 754.12 萬m3，供水水源為地表水，見表2。本次按實灌面積進行分配。

表2 2016年慶安縣和平灌區用水量分配方案Tab.2 Water allocation scheme of irrigation district in qing’an county

3.3 建立灌區農業水權分配指標體系

各層指標的選取應綜合考慮其代表性、獨立性、關聯性、易于量化、簡單、直觀和實用性等特點。并結合研究灌區經濟、社會、環境和自然狀況，選取的指標包含4 個2 級指標、12個3級指標和17個4級指標。具體見圖1。

3.4 評價指標優先序等級

評價指標優先序等級即對指標層中評價指標進行優先程度排序。綜合考慮和平灌區現狀條件和各評價指標實際取值，結合評價指標相對重要程度，對指標層各評價指標隸屬度分級標準進行范圍評定，見表3。

表3 評價指標隸屬度分級標準Tab.3 The classification standard of membership degree of evaluation index

3.5 模糊綜合矩陣的建立和一致性檢驗

根據和平灌區農業水權分配基礎條件，對每一層指標進行標度賦值，引入模糊綜合評價法，建立模糊綜合矩陣。并利用文中1.2.2節中的公式(6)、(7)計算α、β值，檢驗模糊綜合矩陣的一致性，經驗證均滿足要求，見表4～表11。

表4 準則層模糊綜合矩陣Tab.4 The fuzzy judgment matrix of criterion layers

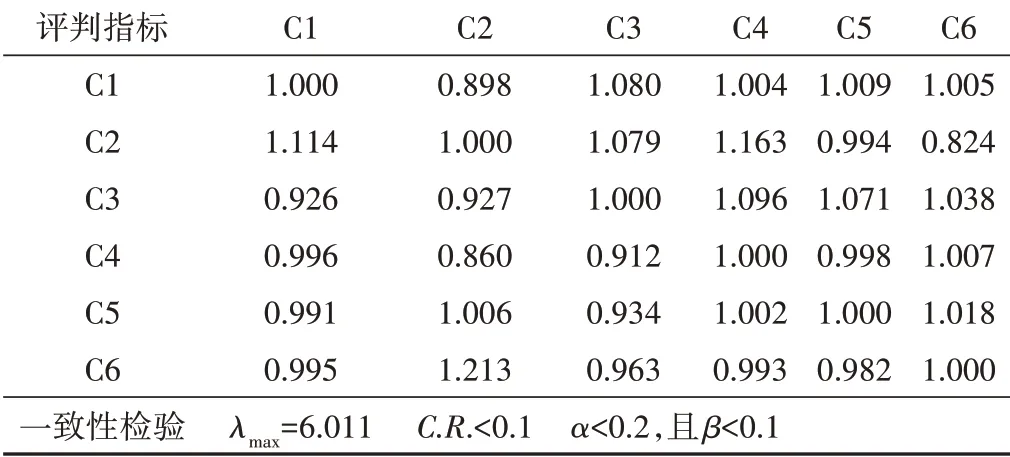
表5 評判層評判指標C1～C6模糊綜合矩陣Tab.5 The fuzzy comprehensive matrix of judging indicators C1～C6

表6 評判層評判指標C7～C8模糊綜合矩陣Tab.6 The fuzzy comprehensive matrix of judging indicators C7～C8

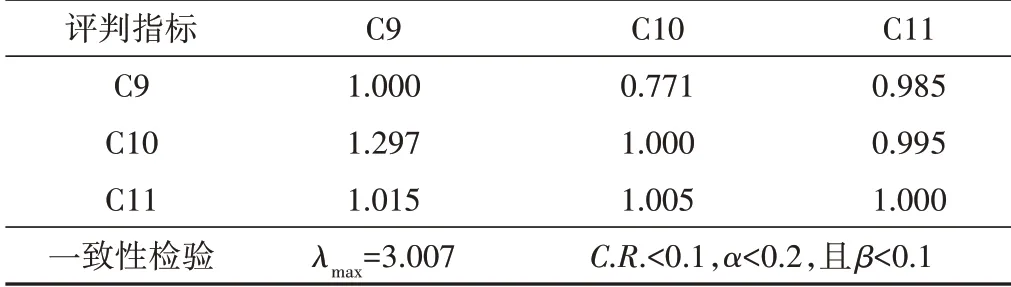
表7 評判層評判指標C9～C11模糊綜合矩陣Tab.7 The fuzzy comprehensive matrix of judging indicators C9～C11

表8 指標層評價指標D2～D3模糊綜合矩陣Tab.8 The fuzzy comprehensive matrix of evaluation index D2～D3

表9 指標層評價指標D7～D8模糊綜合矩陣Tab.9 The fuzzy comprehensive matrix of evaluation index D7～D8

表10 指標層評價指標D9～D10模糊綜合矩陣Tab.10 The fuzzy comprehensive matrix of evaluation index D9～D10

表11 指標層評價指標D15～D17模糊綜合矩陣Tab.11 The fuzzy comprehensive matrix of evaluation index D15～D17

3.6 灌區農業水權分配結果

通過以上計算方法，計算得和平灌區16 條支渠水量分配結果見表12和圖2所示。

表12 和平灌區支渠農業水權分配結果Tab.12 The results of water rights allocation among the branch canals of Heping irrigation district

根據表12 和圖2 中灌區農業水權分配結果，1 支渠、3 支渠、5 支渠、6 支渠、7 支渠、8 支渠、9 支渠、12 支渠、15 支渠、16 支渠模型分配水量均大于現狀按面積分配水量，變幅范圍在-0.09%～-9.90%，2 支渠、4 支渠、10 支渠、11 支渠、13 支渠、14 支渠模型分配水量均小于現狀按面積分配水量，變幅范圍在0.97%～8.62%。根據大量研究表明：水分生產函數因不同作物、不同生育期、不同地區、不同基礎條件而有顯著差異[29-31]。因此，和平灌區不同支渠水分生產函數各不相同，通過模型分配結果能夠實現產量最大化，使水分生產函數計算值高的農田最大程度提高產量，水分生產函數計算值低的地塊幾乎不減產，最終達到經濟效益最大化，為區域經濟發展提供新思路。

4 結論與建議

本文通過改進的層次分析法結合模糊綜合評價法構建的研究灌區農業水權分配模型，得到各支渠水權分配結果。所得結果由不同支渠計量設施配備情況、渠道設施建設情況、節水控灌技術應用、糧食產量、水資源有效利用率、人口因素、灌溉面積、可交易水資源率、經濟效益、收繳水費情況、生態環境等因素綜合影響下決定的，是各層次各種影響因素綜合作用的結果。與現有分配方式即僅根據各支渠面積分配得到的水量結果有一定的偏差，范圍在-9.90%～8.62%。

綜上所述，水利設施配備完善、經濟效益顯著的支渠分配水權大一些，水資源利用率明顯偏低、經濟效益低的支渠分配水權少一些，本文基于分配模型所得結果以經濟效益最大為總目標，帶動當地農業發展，有利于地區經濟長足發展。

（1）在保證公平性及效率性的基礎上，對于灌區各支渠間最終水量分配比例，應綜合考慮優化模型下支渠間水權分配和現狀水資源量分配情況，通過進行公眾參與、民主協商等方式確定。

（2）本次在對和平灌區進行水權分配過程中，強化經濟效益，公平性指標弱化一些，希望未來能健全相關政策，充分體現土地分配中的公平性，給農戶平均分配基礎條件良好、經濟效益高的地塊和基礎條件差、經濟效益低的地塊，以此實現經濟效益最優。

本文所得結果可以給決策者提供技術支持，但在應用于灌區支渠間水權分配時還應與灌區實際情況相結合。