基于概率性能感知演化博弈策略的“云+邊”混合環境中任務卸載方法

雷 鷹 ，鄭萬波，魏嵬，夏云霓，李曉波，劉誠武，謝洪

（1.重慶大學計算機學院，重慶 400044；2.昆明理工大學理學院，昆明 650500；3.西安理工大學計算機科學與工程學院，西安 710048；4.重慶市畜牧技術推廣總站，重慶 401121；5.上海交通大學重慶研究院，重慶 401135）

0 引言

隨著互聯網的普及和物聯網的高速發展，越來越多的移動終端被廣泛運用于人們的日常生活中，預計到2030 年，全球移動終端數接近180 億［1］。移動設備使用量的爆發式增長趨勢是由移動用戶的增加和移動應用程序開發（例如iPhone應用程序和谷歌應用程序）共同作用的結果。與此同時，諸如交互式游戲［2］、增強現實、虛擬現實等新興應用也隨著5G 技術的發展而廣泛普及。這些需要大量計算和能量消耗的應用要想純粹依賴移動設備本身去處理并不現實，有限的計算能力、通信傳輸能力、電池壽命制約著移動設備上新興應用的發展；所以將任務卸載到外部的計算節點，由其提供更為豐富的計算資源，將是解決移動設備資源限制的一種行之有效的方法。

移動邊緣計算（Mobile Edge Computing，MEC）［3］相較于云計算，是將原先本應在網絡中心節點進行的各種計算遷移到網絡的邊緣，靠近用戶側提供服務。通過提供最近端服務，使得應用程序在邊緣側發起時，能夠最大限度減少不必要的數據搬運，減少由此帶來的延遲和能耗，加快網絡響應，降低對中心節點的壓力；同樣也能滿足行業在實時、安全、隱私保護、智能應用等方面的基本需求。在MEC 平臺中，邊緣網絡部署著豐富的小型服務器，為就近的用戶提供豐富的計算能力和資源；只需要將計算密集型任務卸載到邊緣云上，在他們的移動終端上即可享受流暢的應用服務。為滿足動態增加的服務需求，目前常用的是多邊緣節點與中心節點協同為多用戶提供的服務，用戶任務允許被卸載到不同的目標處理位置，包括附近的MEC 節點或中心云上的節點。當任務被卸載到不同的目標處理位置時，可能會產生不同的使用成本。因此，在最大限度地降低資源采購成本方面，應綜合地考慮備選邊緣節點的性能與定價策略。在純粹的邊緣計算環境中，邊緣節點本身的任務處理性能和通信能力往往體現出隨時間波動的動態特性。

針對上述“云+邊”混合環境中的多用戶任務卸載場景，本文提出了一種基于概率性能感知的演化博弈論動態卸載策略。之所以使用演化博弈來解決該問題，是由于傳統博弈論追求的是納什均衡（Nash Equilibrium，NE），需要單個用戶在完全理性的情況下最大化自身收益，從而達到每一個參與者都能接受的平衡狀態。而在“云+邊”混合環境中，地理位置分布的多用戶不具備完全透明的信息和全局的邏輯推演能力，因此并不能達到完全理性。在這種不完全理性狀態下，本文考慮追求種群的最大適應度，進而取得演化穩定策略（Evolutionary Stability Strategy，ESS）。該策略不會因為某一個參與人的決策改變而導致整體再計算，從而節省了大量的決策計算開銷。同時，本文考慮到真實環境中的邊緣云服務器的運行是隨時間動態變化的，是非穩定性的。基于真實的公開的邊緣云服務器的性能數據集和位置分布數據集進行了實驗性案例研究，實驗結果表明，本文所提出的方法在平均用戶期望達成度、平均卸載時延、平均貨幣成本指標上優于傳統的貪婪（Greedy）算法、遺傳算法（Genetic Algorithm，GA）和基于納什均衡的博弈論（Nash-based Game）算法。

1 相關工作

作為移動邊緣計算（MEC）的一個重要主題，移動任務卸載近年來被廣泛研究。部分研究將MEC 環境中任務卸載問題作為一種混合整數規劃（Mixed Integer Programming，MIP），利用最優化方法進行求解。文獻［4］通過將MIP 問題分解為多個凸優化問題并基于Lagrange 乘子的算法來進行求解，但是該方法主要考慮靜態性能參數，無法確保時變波動性能條件下的卸載性能。文獻［5］則基于邏輯的字節分解的求解方法，減小了海量任務卸載請求所帶來的搜索空間，但是該方法主要針對中心化的任務調度場景，無法有效地解決分布條件下的云邊混合環境下的任務卸載。文獻［6］考慮將MEC 環境下任務執行次序作為求解目標，提出了一種基于分支定界的算法進行求解，在保證卸載時的服務質量的同時提高了服務器的收益。此外，當數據規模較大時，啟發式算法也被大量采用。文獻［7］提出了一種基于粒子群優化（Partical Swarm Optimization，PSO）的計算卸載策略以解決工業生產線中的多用戶多MEC 時延優化問題。文獻［8］提出了一個分割時間槽的資源分配算法（Slotted Time Resource Allocation algorithm，STRA）并結合遺傳算法進行最優卸載策略的搜索，能夠明顯提高邊緣節點的利用率，減緩核心網絡壓力。文獻［9］提出了一種基于元啟發式的雙目標優化調度算法，考慮最大限度地縮短最大完成時間并最小化成本。該算法是流行的元啟發式-引力搜索算法（Gravitational Search Algorithm，GSA）與流行的啟發式-異構完成時間（Heterogeneous Earliest Finish Time，HEFT）算法的混合體，并通過引入一個稱為成本-時間等效的因子將雙目標優化問題轉化為一個帶約束條件的單目標優化問題來求解。而文獻［10］提出了一種多目標細菌覓食優化算法（Multi-Objective Bacterial Foraging Optimization Algorithm，MOBFOA），通過應用帕累托最優前沿技術對原始的細菌覓食優化算法（Bacterial Foraging Optimization Algorithm，BFOA）進行改進以處理多目標優化調度問題，其改進主要是從占優和非占優前沿中選擇細菌的位置以獲得解的多樣性。隨著機器學習的發展，文獻［11］提出了一種分布式深度神經網絡（Deep Neural Network，DNN）模型，使用半定松弛的二次約束線性規劃對DNN 模型進行訓練，得到最優卸載策略。文獻［12］考慮了優勢系統模型中的多任務多服務卸載場景，并提出了一種基于深度強化學習的在線卸載決策方法。文獻［13］將能量消耗和延遲作為卸載目標，文獻［14］以最小化時延和成本作為求解目標，提出了一種分布式博弈理論方法來進行卸載策略的選擇。文獻［15］提出了基于博弈論方法的在線卸載算法，能實現在一臺邊緣服務器與多個用戶的網絡場景中開展在線自組織的任務分配和卸載，并通過博弈算法求解納什均衡來指導用戶選擇合適的網絡信道進行卸載。文獻［16］將進化博弈運用于邊緣節點卸載問題中，討論用戶在非理性的情況下達到ESS，但是它主要考慮純邊緣計算的環境，而非本文研究的“云+邊”混合環境。

以上研究，均將邊緣服務器的性能視為一個恒定的常量輸入決策或優化模型，以獲得任務調度和卸載的決策方案。然而，真實環境下的邊緣服務器或邊緣計算節點的性能，因為通信傳輸、能源供給、任務負載等不確定因素的影響，往往體現出隨時間變化和波動的特點。采用恒定或靜態的性能參數或測試值作為調度算法的輸入，將導致算法生成的調度策略難以在性能波動的系統中取得穩定的調度效果。針對上述問題，本文通過歷史經驗概率分布函數來描述性能的波動變化，并將用戶的收益進行概率化計算處理。

2 系統和計算模型

2.1 系統模型

本文假設云服務器和邊緣服務器都有各自的覆蓋范圍，覆蓋范圍內的終端用戶可以通過無線訪問連接到它［17］。邊緣服務器分布式地部署到蜂窩基站附近從而為用戶就近提供服務。同時考慮一個由單個宏基站和K個微基站組成的異構網絡來承載邊緣計算環境。為了保證某一地理區域中的N個用戶都能獲得中心云服務，中心云服務器部署在宏基站上。中心云服務器可以以一個較大的覆蓋范圍為終端用戶提供服務。而K個微基站上則分別部署K個邊緣服務器，在更靠近終端用戶的位置上為他們提供邊緣云服務。邊緣服務器的計算能力、存儲資源以及覆蓋范圍都要比中心云服務器小，為用戶提供的計算處理性能也更低，但是價格卻較低。根據文獻［16］的分析，上述云邊混合環境的區域，通常可被劃分為J個小服務區域，每個區域內的用戶被視為一個群體，劃分的原則是確保每個區域的邊緣服務器數量幾乎相等，同時每個區域內用戶的數量不超過邊緣服務器數量的10 倍。每個區域的用戶所構成的種群，在有限理性假設下，以固定的比例采取相同的博弈策略。

圖1 給出了一個代表性的例子，闡述上述混合環境。在本例中，存在一個集中式的中心化云服務器（CS0）、6個邊緣服務器（CS1～CS6）和9 個用戶（U0～U8）。不同邊緣服務器的覆蓋區域可能重疊，因此用戶可以選擇多個候選服務器進行任務卸載。例如，可以將U1的任務分配卸載給CS0、CS1或CS2，然而U6只能將任務卸載到CS0上進行處理。將區域劃分為三個大小相同的區域（R0～R2），每個區域都部署兩臺邊緣服務器。

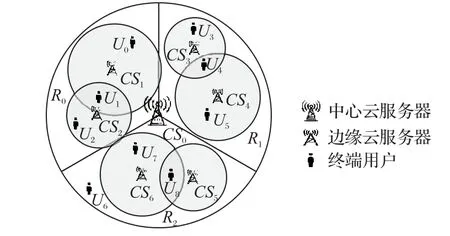
圖1 云邊混合環境Fig.1 Hybrid cloud-edge environment

本文使用的變量信息如表1所示。

表1 參數具體信息Tab.1 Specific information of parameters

2.2 計算模型

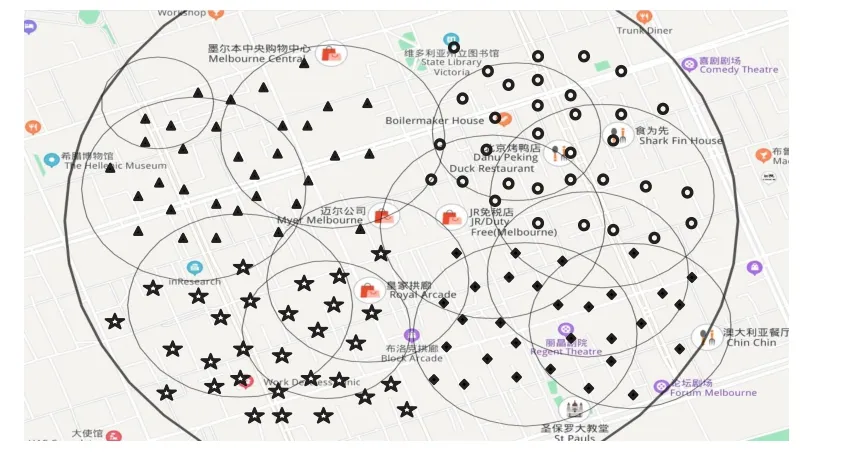
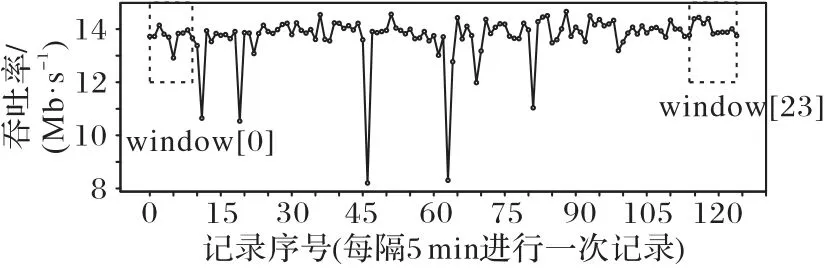
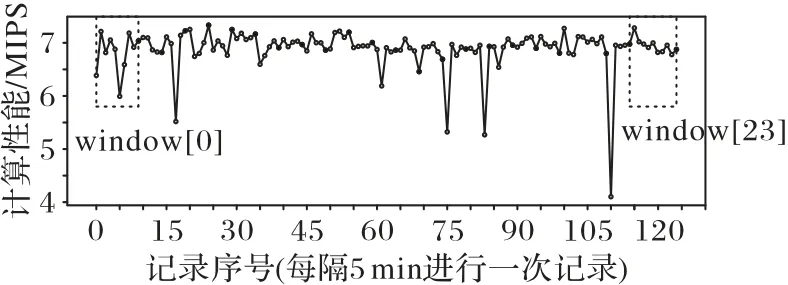
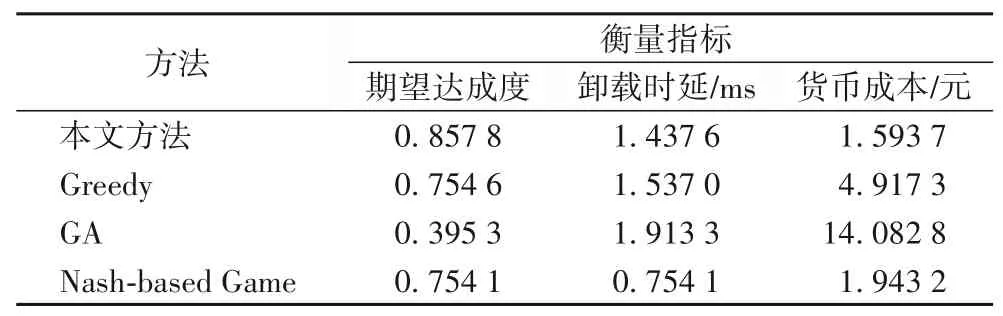
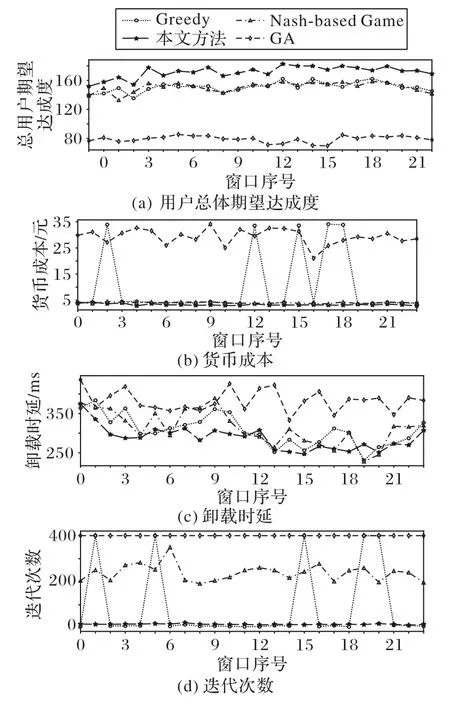
對于用戶Ui而言，首先要確定其與各服務器之間的距離。若滿足dist(i，k)

其中，ηi，k=(i，k)是與距離有關的參數，用戶與服務器之間距離越遠，誤碼率越高，平均傳輸速度就會越低，wk和fk分別表示CSk的平均帶寬和平均計算能力。fk可根據其對應的歷史經驗分布［19］計算，計算式如下：

根據式（3），用戶的貨幣成本包括三部分，即通信成本、計算成本和租用服務器的費用。Ct，k和Cf，k分別表示CSk單位傳輸速率的價格和單位計算資源的費用。Vrent，k與服務器的當前負載有關。如果服務器的使用效率更高，并且為更多的用戶提供服務，則每個用戶分攤的租金就越低，因此用戶Ui的卸載成本為：

本文使用USi來表示Ui的用戶期望達成度，它可以表示為卸載時間和貨幣成本約束都得到滿足的概率：

代表區域內Pj的期望達成度，其中numj表示Pj中的用戶數量：

US是整個區域的期望達成度，并將其作為最終優化目標：

3 演化博弈

演化博弈相較于經典博弈論，區別在于其側重于對博弈主體的動態均衡［20］的研究，而不同于經典博弈論所研究的靜態均衡。動態均衡是在參與人以不完全信息為條件、有限理性為前提下研究的一種動態分析過程。所謂有限理性，即指參與人具有一定的統計分析能力，能夠在一定的限度下判斷不同策略組合下的開銷和收益程度，而有異于完全理性所具備的完全的信息搜索能力、邏輯計算能力和對未來的預測能力。演化博弈論正是將傳統博弈論和動態演化過程結合在一起進行分析的一種理論，用以分析參與人在有限理性下，對資源配置行為及博弈策略的選擇。演化博弈的研究對象是群體，基本思想為：賦予群體一個最開始的形態，然后在時間演化過程中，群體中的參與者自由地去選擇更優的策略。

由于每個邊緣服務器的計算資源和帶寬資源的限制，不同區域的終端用戶不得不競爭中心云服務器的資源。這種多分布資源節點、多用戶競爭的場景，與演化博弈所研究的理論模型高度契合。

3.1 博弈標準式

經典博弈標準式包括三個因素：博弈的參與者、每個參與者可供選擇的策略集合和針對所有參與者可能選擇的策略組合，以及每個參與者在選擇策略時的收益函數。在演化博弈的背景下，群體可被用來代表一組具有相同的性質的參與者［21］。

將演化博弈的形式設計如下：

1）參與者。對于圖1所示的“云+邊”混合多用戶環境，區域內的每個終端用戶都是演化博弈中的參與者。在有限理性的假設下，參與博弈的目的是通過參與博弈實現自身效益最大化。

2）群體。如圖1所示，參與者們按照位置可劃分為J個不同的群體，每個群體中的用戶數量用numj表示。用{P0，P1，…，PJ-1}來表示J個群體的參與者集合，每個群體中的參與者都位于同一地理區域并滿足所有群體的用戶數之和為總用戶數。

3）策略。每個參與者的策略是指它所能選擇的服務器，在該博弈環境中共有1+K種服務器可供參與者選擇，使用xk來表示用戶是否選擇服務器CSk進行任務卸載的實際情況：

6）收益。參與者的收益取決于其凈效用函數（4），由其最大可容忍時延和成本以及實際產生的時延和成本決定。則Pj群體的用戶Uj選擇CSk服務器上所獲得的收益可以表示為：

3.2 演化穩定策略

在傳統博弈中，所有參與人都可以達到一個穩定狀態，即沒有參與人可以通過單方面改變策略來進一步獲得額外的利益，這種狀態稱為NE。將混合構架下服務器的選擇及資源分配看作一個博弈Γ，參與者集合為N，策略集合為S=[s1，s2，…，sN]表示對每個參與者的策略進行了統計。用S-i=[S1，…，Si，Si+1，…，SN]表示除開參與人Ui以外其他人所選擇的策略組合。在收益集合Π=[π1，π2，…，πN]中，參與人Ui的收益與自己選擇策略和他人選擇策略有關，表示為π(si，s-i)。

定義1一個博弈Γ=〈N，S，Π〉的納什均衡解S*=

納什均衡具有一種自我強化的特性，即每個參與者都沒有動機偏離這個均衡。獲得納什均衡的一般解是基于所有參與者完全理性的假設。然而，在一個小擾動下，所有參與者都可能改變策略，以達到另一個納什均衡。在進化博弈論［21］中，保持有限理性的參與人所達到的一種穩定狀態可以抵抗小干擾，這種均衡稱作EE（Evolutionary Equilibrium），達到該均衡的策略為ESS。

與納什均衡相比，定義2的條件1）保證了EE 是納什均衡（NE）。定義2 的條件2）保證了博弈過程的穩定性。在策略演進過程中，使用變異策略的玩家將減少，直到群體中的所有參與者漸近接近EE。在本文的問題中，云邊混合構架下的終端用戶在一組有限的策略中調整他們的策略以獲得更好的回報。在每一時刻，終端用戶都可以獲得自己的策略集，同時獲得所在群體的平均收益信息，從而隨著時間的推移，不斷地演進自己的服務器選擇策略。經過足夠多的重復和推演，使用其他策略的突變參與者會因為收益較低而數量不斷減少，最后突變玩家滅絕，達到群體的演化穩定狀態。這個動態的過程可以通過復制動態方程進行求解。下一節將對此進行詳細描述。

3.3 復制者動態方程

演化博弈模型主要是基于突變機制和選擇機制建立起來的模型，突變指的是在一個群體中，小部分參與者以隨機的方式選擇不同于大部分參與者的策略，選擇的策略可能獲得較高的收益，也可能獲得較低的收益，但是只有優秀的策略才不會被歷史淘汰，而被保留下來。選擇則是指該策略能夠獲得更高的收益，能在以后不斷地被其他參與者采用。這種選擇機制正是復制者動態模型的關鍵，它提供了一種獲取他人群體信息的方法，并向均衡點收斂，直到策略適應以達到演化均衡（EE），即群體不會改變其選擇。其基本思想是在有限理性的博弈者群體中，結果優于平均水平的策略將逐漸被更多的博弈者所采用，博弈者策略的比例也隨之發生變化。具體如下：

其中δ用來控制同一群體中參與者策略適應的收斂速度。增長率(t)表示對時間進行一階求導得到的函數，(t)是群體中的參與者選擇服務器CSk時所獲得的當前收益，(t)為t時刻群體的平均收益，可以通過式（10）計算得到：

基于在群體Pj中策略選擇的復制者動態方程，當選擇策略s的收益高于同一群體的平均收益時，選擇該終端用戶的數量在總體上將呈正增長趨勢。通過設置=0，可以得到復制者動態的不動點，在該不動點上，由于同一群體中的所有參與者都有相同的收益，因此群體狀態不會改變，也沒有參與人愿意改變策略。

基于復制者動態的算法描述如算法1所示。

4 實驗和結果分析

4.1 數據集

為了驗證本文所提出方法的正確性和有效性，基于EUA（Edge User Allocation）數據集［22］提供的邊緣服務器與用戶的位置和針對邊緣服務器性能的數據集［23］進行了模擬實驗。圖2 顯示該區域包含200 個終端用戶、1 個中心云服務器和12個邊緣云服務器。邊緣云的服務半徑在100～300 m，中心云服務器的覆蓋范圍設定為800 m。服務器的覆蓋范圍使用圓圈表明。根據地理位置信息，將該區域劃分成4 個小區域，每個小區域中的用戶被看作一個群體，分屬于不同群體的用戶用不同圖形進行標注。

圖2 實驗數據的地理分布情況Fig.2 Geographical distribution of experimental data

對于中心云服務器的性能數據，測試了一個典型的第三方商用云服務，即騰訊云。圖3～4 顯示了中心云服務器的吞吐量和計算性能（以每秒百萬條指令（Million Instructions Per Second，MIPS）為單位），另外12 組邊緣云服務器的性能統計圖與之類似，這些數據被劃分為24 個連續的時間窗口，每個窗口記錄相鄰10 次記錄，以便于在不同的時間階段測試和比較不同策略的性能。

圖3 處于不同時間窗口的中心云服務器的吞吐量Fig.3 Throughput for central cloud server at different time windows

4.2 對比方法

將本文提出的方法與以下三種經典方法進行了比較。

1）貪心（Greedy）算法［24］。在求解問題時只考慮當前最優的結果，而不從整體去考慮，忽略整體策略的改變對當前局部策略的影響。

2）遺傳算法（GA）［25］。該算法模擬生物自然選擇和基因遺傳，通過對策略集合進行多代的選擇、交叉和變異過程，不斷向最優解靠攏。

3）基于納什均衡的博弈論（Nash-based Game）算法［15］。假設每個參與人都是完全理性的，為使個體收益最大，博弈最后會趨向一個均衡點，使所有參與人都不會優先改變策略。

圖4 處于不同時間窗口的中心云服務器的計算性能Fig.4 Computational performance for central cloud server at different time windows

4.3 對比結果分析

通過對24個窗口信息求離散概率分布，每個窗口進行50次實驗求平均值，將參數設置為ξ=0.1、λ=2、δ=0.4、ε=0.05，可得到圖5 的結果。通過分析，得出以下幾個結論：1）在所有24 個時間窗口中，本文方法的總用戶期望達成度和卸載時延都優于其他算法，總用戶期望達成度為171.6，平均用戶期望達成度為85.8%；2）本文的方法和基于納什的博弈算法在貨幣成本方面明顯優于其他方法，平均貨幣成本為Greedy 算法的11.3%，且比GA 更穩定；3）本文的方法在所有窗口下都比其他算法具有更少的迭代次數，均能在10 次迭代內達到穩定狀態。

綜合考慮卸載時延和貨幣成本得到的用戶總體期望達成度，本文提出的方法在多次實驗后，在每一個窗口都表現比較好，但是將其分為兩個單獨的指標，其他方法也會得到更好的結果。

圖5（b）中，Greedy 算法得到的貨幣成本在多個窗口下表現略微優于本文提出的方法，但在多個窗口（w=2，12，15，17，18），該指標又表現極端糟糕，總體表現沒有兩種博弈論方法穩定。

圖5（c）中，Greedy 算法和Nash-based Game 算法在多個窗口（w=12，19）上的卸載時延都略低于本文的方法，表現更優，但本文的方法在更多窗口表現出相較于這兩種算法的顯著優勢，且整體表現更加穩定。同時可見，該方法通過群體的動態迭代和學習，表現出更好的環境適應性。

具體來看，對24 個窗口求平均值可得到的平均性能指標如表2所示。

表2 不同方法在不同衡量指標下的平均值對比Tab.2 Comparison of average values of different methods under different measurement indexes

其中，本文提出的方法在平均用戶期望達成度方面相較于Greedy、GA 和Nash-based Game 方法分別提升了13.7%、117.0%、13.8%，平均卸載時延分別降低了6.5%、24.9%、8.3%，平均貨幣成本分別降低了67.9%、88.7%、18.0%。

圖5 是在得到最優卸載策略后用戶執行卸載時所產生的成本和時延開銷。若將服務器計算推演算法的用時考慮進去，如圖5（d）所示，本文的方法表現出最低且最穩定的迭代次數，一定程度上加快了服務器對用戶的響應，提高了用戶的滿意度。

圖5 不同時間窗口下不同衡量指標的比較Fig.5 Comparison of different measurement indexes at different time windows

4.4 引入突變后的結果分析

由于GA 在復雜環境中在多個指標上都表現出局部最優，不能在合理時間內得到最優解，而Greedy 算法又表現出極不穩定性，故本節將著重研究兩種博弈論算法，即基于納什均衡的博弈論算法和本文所提出的演化博弈論算法，主要研究在用戶突變后的響應。

通過實驗比較了兩種博弈論算法對變異后種群的收斂性。首先，群體均達到了穩定狀態1（NE1或EE1）。經過五次迭代，群體中的少數用戶將隨機變異，表現為用戶任務的大小發生變化，可容忍的延遲和成本也會發生變化。突變后，群體通過重新調整卸載策略以達到穩定狀態2（NE2 或EE2）。本文將在某一博弈論策略下，突變后重新達到新的穩定狀態（NE或EE）的迭代次數作為群體收斂性的度量。

如圖6 所示，使用傳統博弈論算法，參與者在變異后需要經過10 次迭代才能達到新的穩定狀態，而演化博弈算法（本文方法）在圖7 中只需要一次迭代就可以達到新的穩定狀態。實驗結果表明，本文方法在抗干擾能力方面優于傳統方法。

圖6 基于納什均衡的博弈論的收斂性Fig.6 Convergence of Nash-based Game

圖7 基于演化博弈的收斂性Fig.7 Convergence of evolutionary Game

5 結語

本文研究了具有非穩定性能的“云+邊”混合環境中的任務卸載問題，提出了一個基于歷史性能數據概率分析與演化博弈的多用戶卸載方法。為了驗證所設計方法的正確性和有效性，基于一個公開的云/邊緣資源位置數據集設計模擬實驗，將本文的方法與傳統的Greedy、GA 和Nash-based Game 方法進行了比較。實驗結果表明，本文所提出的方法在平均用戶期望達成度、平均卸載時延、平均貨幣成本指標上優于對比方法。

在今后的擴展研究中，將進一步開展以下工作：1）考慮用戶和邊緣節點的移動性，研究在非規則移動軌跡下多用戶的任務在線卸載的策略；2）引入基于時間序列和神經網絡的性能預測模型，并用軌跡預測信息和性能預測信息，驅動多用戶任務卸載決策的模型；3）考慮在非可信通信條件下，任務失效和傳輸故障對任務卸載的影響，設計故障容忍和容錯的多用戶任務卸載的策略和算法。