基于多種群組合策略的人工蜂群算法

李文霞，劉林忠，代存杰，李玉

（蘭州交通大學交通運輸學院，蘭州 730070）

0 引言

近年來，隨著群智能優化算法的高效發展，其在解決復雜優化問題時體現出良好的求解性能，受到學者們的廣泛關注，群智能優化算法源于對自然界中生物群體行為的模擬，主要包括遺傳算法［1］、蟻群算法［2］、粒子群算法［3］、人工蜂群（Artificial Bee Colony，ABC）算法［4］等。遺傳算法對自然界中生物的自然淘汰進化過程進行模擬，主要通過交叉、變異、選擇算子來實現，該算法的改進方向包括自適應算子的引入［5］、多種群方式的改進［6］、編碼技術的改進［7］及混沌理論的加入［8］等角度；蟻群算法模擬螞蟻覓食行為，通過信息素的正反饋機制尋找自蟻巢到食物源的最短路徑，近年來蟻群算法的改進主要集中在信息素的更新策略［9］及路徑選擇策略［10］兩個方面；粒子群算法對生物界鳥類覓食行為進行模擬，通過對全局極值的對比，及時調整粒子的搜索速度與方向，相關學者從粒子群多樣性的控制［11］、算法中參數的改進［12］、初始化過程中粒子拓撲結構的優化［13］等方面出發對算法進行改進。上述群體智能算法的優化改進逐漸趨于成熟，一些新型群體智能算法的提出受到了國內外學者的廣泛關注。

受蜜蜂群體覓食行為啟發，Karaboga［4］于2005 年提出了人工蜂群（ABC）算法。相較于其他群體智能算法，人工蜂群算法中的勞動分工和協作機制有效提高了算法的全局搜索能力，同時正反饋的尋優策略加快了全局尋優過程，求解效率更高，并且在求解連續優化問題和組合優化問題時均表現出優越的性能，具有廣泛的適用性，已在神經網絡訓練［14］、系統工程設計［15］、聚類分析［16］和圖像信號處理［17］等眾多領域得到了廣泛應用。

ABC 性能主要取決于搜索方程和個體選擇策略，基本ABC 的搜索方程包含隨機個體信息較強，相較于一般群體智能優化算法，表現出良好的全局搜索優勢，但同時存在收斂速度慢、求解精度低、易陷入局部最優等問題。算法的全局搜索和局部開發在求解過程中表現出互補性，但在操作上又具有矛盾性，為更好地平衡二者，同時滿足求解效率和求解精度要求，相關學者從搜索機制改進和融合算法等方面進行了有效研究。向萬里等［18］將最優個體指導信息引入雇傭蜂階段，利用個體信息對跟隨蜂的擾動，進一步平衡探索能力和開發能力。Kiran等［19］考慮算法的下降梯度，對較強地位的維度進行搜索，以提高算法的搜索深度。孟紅云等［20］利用精英信息、隨機信息及鄰域信息指導雇傭蜂階段搜索，同時在觀察蜂階段提出全局精英信息和當代最優信息指導搜索，使算法的尋優能力得到顯著提高。Jadon 等［21］受差分進化（Differential Evolution，DE）思想的啟發，提出具有差異進化的混合人工蜂群（Hybrid Artificial Bee Colony with Differential Evolution，HABCDE）算法，將DE 和ABC 融合，以提供良好的搜索平臺，在提高搜索的深度的同時不影響探索的廣度。魏鋒濤等［22］為提高種群多樣性，構建了混沌反向解初始化機制，并構建跟隨蜂量子更新搜索策略，進一步地提高蜜源鄰域內的尋優質量。

上述算法改進在不同程度上提高了ABC 的尋優能力，但仍有較大改進空間，如何進一步提高算法的應用范圍、收斂速度及收斂精度，仍需深入研究，因此本文提出了一種基于多種群組合策略的人工蜂群（Artificial Bee Colony based on Multipopulation Combination strategy，MCABC）算法。為提高算法搜索效率，針對雇傭蜂和跟隨蜂分別設計不同的組合策略，在跟隨蜂階段劃分了自由種群和非自由種群，針對不同屬性的個體采用對應的子策略；同時在搜索方程中改進了維度信息更新機制，進一步提高了算法在高維復雜函數的求解性能。為驗證本文提出算法的有效性，采用15 個標準測試函數，將MCABC與多個具有代表性的改進ABC算法進行對比，進一步驗證了算法的尋優性能。

1 標準人工蜂群算法

人工蜂群算法思想來源于仿生學中蜜蜂群體覓食行為，蜂群個體分為雇傭蜂、跟隨蜂和偵查蜂3 種類型，雇傭蜂和跟隨蜂數量各占蜂群總數一半，偵查蜂數量與雇傭蜂相同，雇傭蜂負責勘察并將蜜源信息分享給跟隨蜂，跟隨蜂依據蜜源質量通過輪盤賭方式選擇，并在附近尋找更好的蜜源，當某一蜜源被舍棄時，雇傭蜂轉化為偵查蜂尋找新蜜源，三種蜂群發揮各自效用，準確有效完成蜜源的搜索和采集任務。

1.1 初始化

在標準ABC 中，當前解空間通過式（1）初始化種群，一個蜜源位置代表問題的一個可行解，蜜源的位置用D維向量表示Xi=[xi1，xi2，…，xiD]，其中：

其中：i=1，2，…，SN，SN是解（蜜源）的數量，j=1，2，…，D，D是解的維數；xi，j是第i個解的第j維；?i，j是［0，1］的隨機數；、是j維的上、下界。

1.2 雇傭蜂

雇傭蜂通過式（2）在初始解附近搜索新解，進行局部搜索，并對每個蜜源的適應度進行計算，進而評價食物源的優劣，若新解優于初始解，則保留新解，迭代重復值Counter（i）加1；否則保留初始解，迭代重復值Counter（i）不變，即通過貪婪選擇更新解同時記錄蜜源開采情況。

其中：vi，j是更新后的解；xk，j是在種群中隨機選擇與xi，j不相同的解；φi，j是［-1，1］的均勻隨機數。

1.3 跟隨蜂

跟隨蜂依據雇傭蜂傳遞的蜜源信息，通過式（3）輪盤賭概率選擇某一蜜源，蜜源的適應度值越高，可行解的質量越好，被選擇的概率越大。隨后跟隨蜂采用式（2）進行鄰域搜索，并采用貪婪選擇更新解，在保留優勢個體的同時兼顧蜜源的探索能力。

其中：pi是解i的選擇概率；fiti是解i的適應度值。

其中：fi是目標函數值。

1.4 偵查蜂

當某一蜜源長期未更新時，當前蜜源將被遺棄，雇傭蜂轉變為偵查蜂，通過式（1）隨機產生新蜜源，算法進入雇傭蜂階段。偵查蜂的操作有效避免了算法過早陷入局部最優，提高了算法的全局探索能力。

2 基于多種群組合策略的人工蜂群算法

2.1 研究思路

標準ABC 受制于搜索策略的單一和搜索方程的信息匱乏，算法的搜索導向性和多源信息的融合性較弱，表現為一種隨機的無向搜索，這種無向搜索雖然一定程度上增強了全局探索能力，但同時也降低了收斂速度和求解精度，且迭代過程中只更新D維中隨機選擇的一個維度，使其在求解高維函數時尋優能力下降。鑒于此，本文針對雇傭蜂和跟隨蜂分別設計組合策略CS1和CS2。在雇傭蜂階段采用CS1策略，以提高初始種群的深度與廣度；在跟隨蜂階段，為進一步明確跟隨蜂個體的任務重點，針對自由子集和非自由子集，采用CS2 策略，其中，自由個體增強探索能力，非自由個體側重開發能力；最后，在搜索方程中融入異維單點更新和多維匹配更新機制，以提高算法在高維問題中的優化效率。

2.2 維度更新機制

ABC中固有的同維單點更新機制能夠有效勝任低維問題的求解，而這種單一的更新模式在面對高維問題時求解效率顯著下降，既有研究證明，異維搜索避免了ABC 單一搜索模式的局限性，增強了算法的全局搜索能力，有利于算法擺脫局部最優［23-24］。為此，本文將多維匹配更新機制和異維單點更新機制引入搜索方程，有效利用多維信息的并行優化和異維信息的協同交互，提高算法在求解高維問題時的精度。多維匹配更新示意如圖1所示，異維單點更新示意如圖2所示。

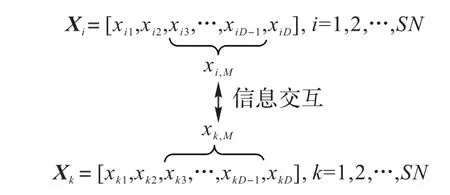
圖1 多維匹配更新示意圖Fig.1 Schematic diagram of multi-dimensional matching update

圖2 異維單點更新示意圖Fig.2 Schematic diagram of different-dimensional single point update

2.3 雇傭蜂組合策略CS1

對于標準ABC 算法，雇傭蜂主要借助式（2）在當前解i的鄰域內進行一次擾動，主要包括三個隨機項j、k、φi，j，隨機項j確定某一具體更新維度，隨機項k確定用于更新的另一個解，這種更新模式使初始解僅在對應的同一維度內更新鄰域，雖然表現出一定的全局探索性，但局部開發性較弱。因此，為達到立體式搜索效果，采用一種組合策略CS1 來平衡算法的探索和開發能力。

CS1-1 搜索方程中包含了四個隨機項M、k、h、φi，j，加強廣度探索：

其中：M是多維匹配更新的維度數；k≠h≠i且k，h∈{1，2，…，SN} 是隨機選擇的個體下標。M個維度的多維匹配更新在最大限度上保留了初始解的有效信息，同時在一定程度上保證了鄰域搜索的均衡性，而隨機項k、h提高了解在鄰域內的探索能力，擴大了搜索空間，即CS1-1策略兼顧了雇傭蜂鄰域搜索的廣度與深度。

CS1-2側重于深度開發，與文獻［20］中式（3）“vi，j=xbest，j+φi，j(xbest，j-xi，j)”不同，式（5）避免了xbest，j與xi，j差距過大時導致的擾動過大，最大限度保留了精英個體的有益信息，提高了搜索效率。

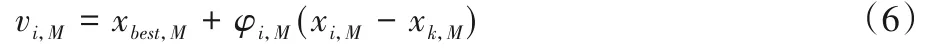
其中：xbest是每一代中適應值最高的精英個體。

雇傭蜂隨機選擇CS1-1 和CS1-2，在全局探索的同時兼顧對最優個體的開發。

2.4 跟隨蜂種群劃分

在跟隨蜂階段，將種群劃分為自由子集和非自由子集，如圖3 所示。為兩類個體賦予特定的職能，其中自由個體適應值與精英個體適應值相差較大，潛在的開發效益較差，可以加強其探索能力來搜索額外的解空間；非自由個體的適應值與精英個體的適應值的差異較小，有更好的挖掘潛能，可以賦予其在非自由子集范圍內的開發能力，以加強算法在優勢個體的深度搜索。跟隨蜂中非自由個體搜索通常情況下比自由個體搜索跨度要小，兩種策略的結合在深度和廣度上加強了算法的搜索能力。

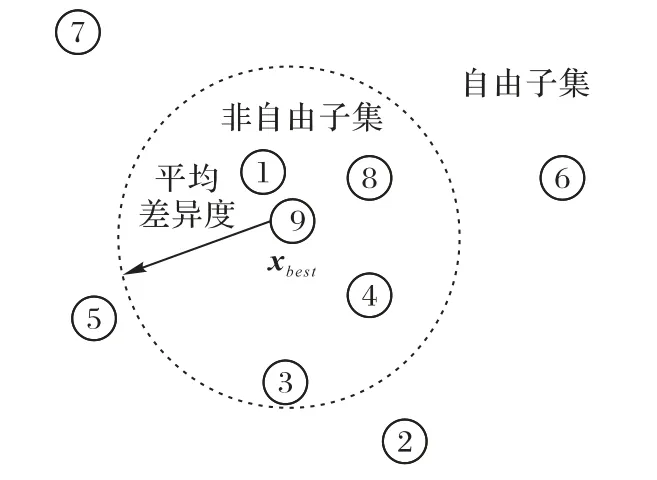
圖3 種群劃分Fig.3 Population division

平均差異度dt作為劃分種群的依據：

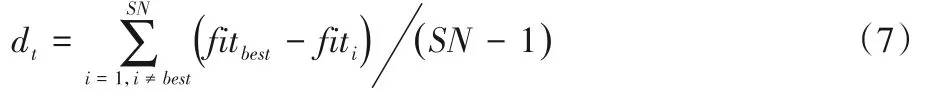
其中：dt是第t代循環適應值的平均差異度；fitbest和fiti分別是精英個體和第i個體的適應值。

計算當前個體適應度fiti與最佳個體適應度fitbest的差值，比較差值與平均差異度dt的大小，若差值大于平均差異度，即超出以平均差異度為半徑的范圍，則當前個體視為自由個體；反之，當前個體視為非自由個體，以此來進行種群劃分。

2.5 跟隨蜂組合策略CS2

在跟隨蜂階段，經過輪盤賭選擇后，當跟隨蜂選擇的是自由個體，通過兩個隨機個體和當前個體構建探索的子策略CS2-1，包括M、p、q、φi，j四個隨機項，使其在整個解空間內進行隨機搜索：

其中：p≠q≠i且p，q∈{1，2，…，SN} 。

非自由個體具有成為下一精英個體的潛在優勢，而多源信息交互是改善搜索性能的有效手段，因此，當跟隨蜂選擇的是非自由個體，則通過當前個體、精英個體和非自由子集中的隨機個體構建CS2-2 子策略，在非自由子集范圍跨越維度深度開發，以期發現未知的優勢個體：

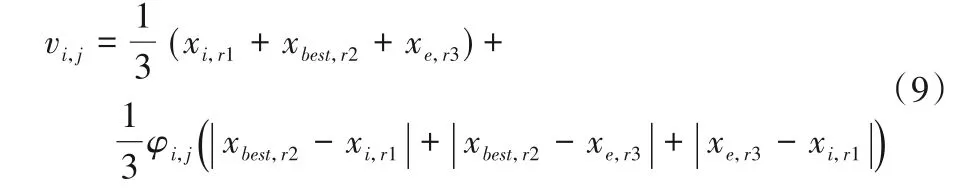
其中：xe是非自由子集中的隨機個體；r1≠r2≠r3且r1，r2，r3∈{1，2，…，D} 。

式（8）與文獻［20］中式（12）在方程結構上很相似，需要注意的是，在文獻［20］中式（12）是利用精英解的有益信息和同維單點更新機制，相應的，式（8）采用的是非自由子集中隨機個體的有益信息和異維單點更新機制，在擴大有益解空間的同時有效利用了異維信息的協同優化。

2.6 MCABC流程

算法迭代過程中，雇傭蜂隨機選擇子策略CS1-1 或CS1-2更新初始化種群個體，通過與初始化種群貪婪選擇保留當前優勢個體；以個體適應值和最佳適應值的平均差異度比較作為種群劃分標準對當前優勢個體進行種群劃分，為跟隨蜂階段作準備；通過輪盤賭方式對跟隨蜂進行選擇，針對自由子集跟隨蜂采取CS2-1子策略，非自由子集跟隨蜂采取CS2-2子策略，在進行貪婪選擇后更新自由子集和非自由子集；對于達到未更新次數的個體進行初始化。不斷循環上述過程，直到滿足算法停止條件，算法流程如圖4所示。

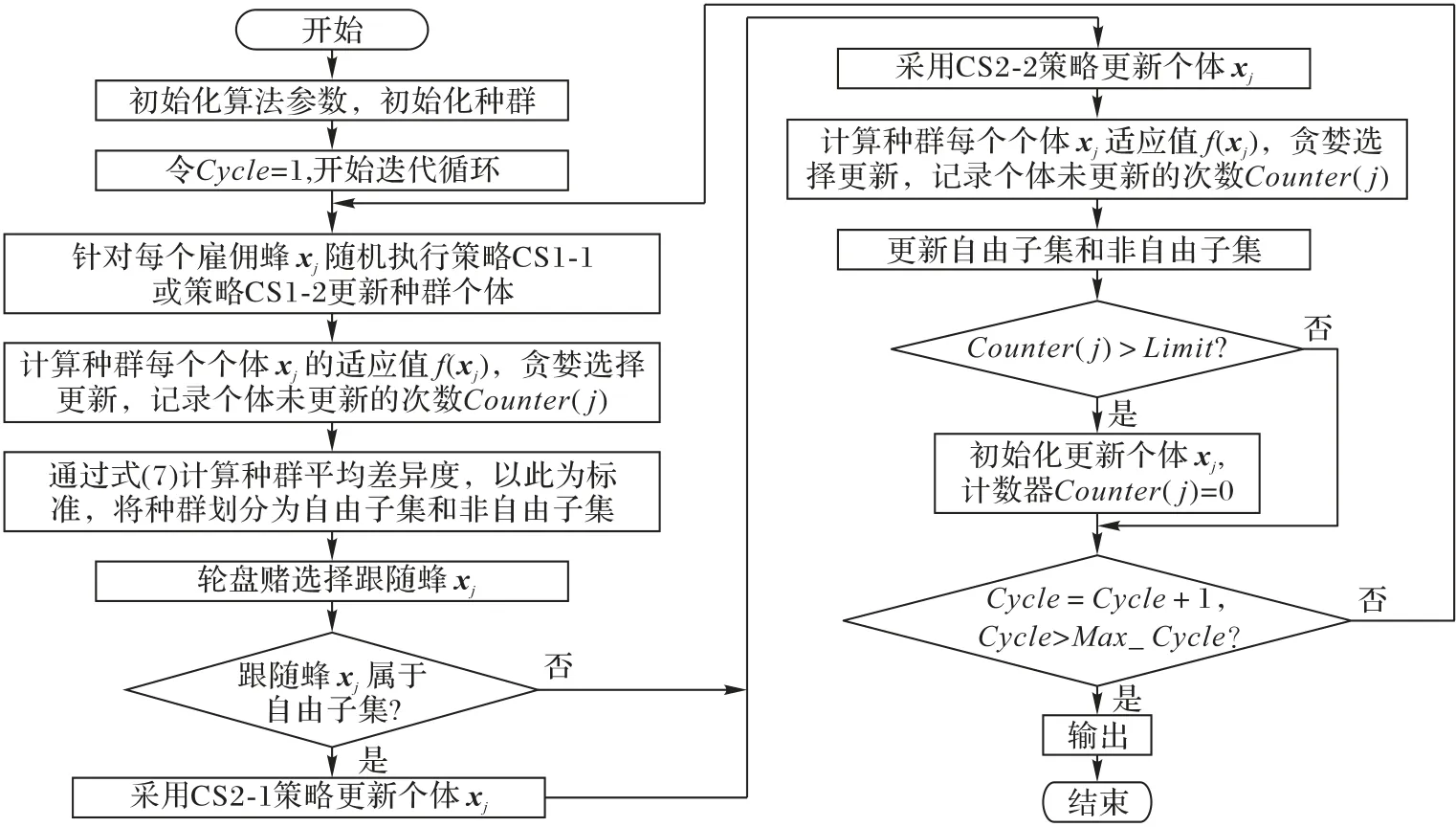
圖4 MCABC算法流程Fig.4 Flow chart of MCABC algorithm

2.7 MCABC偽代碼

MCABC偽代碼如下：

2.8 算法復雜度分析

MCABC 算法在雇傭蜂階段和跟隨蜂階段分別引入了兩種不同的種群更新策略。在雇傭蜂階段，種群個體通過隨機方式選擇策略CS1-1和策略CS1-2進行更新，該過程不增加算法的時間復雜度。在跟隨蜂階段，涉及循環前的種群整體劃分和循環中的種群動態劃分，在循環前，需依據種群個體適應值和精英個體適應值的平均差異度作為種群劃分的標準，首先依據適應度值對整個種群進行排序操作（對總體排序）選擇出精英個體，其時間復雜度為O（SN·log（SN）），然后通過式（7）計算種群平均差異度，以此標準對種群整體進行劃分；在循環過程中，每次循環后需判斷當前更新個體是否為精英個體，更新當前個體后通過式（7）計算種群適應值的平均差異度來動態劃分種群，該過程不涉及排序操作，不額外增加算法的時間復雜度。

因此，與ABC 算法相比，MCABC 算法在雇傭蜂階段開始前劃分種群過程時引入了額外的計算，由于ABC 算法的時間復雜度為O（SN·D），因此，MCABC算法時間復雜度為O（SN·D+SN·log（SN）），由于D遠大于log（SN），MCABC 算法的時間復雜度可以簡化為O（SN·D），可見相較于經典ABC 算法，MCABC算法具有相同的計算時間復雜度。

3 實驗仿真與結果分析

3.1 測試函數實驗結果

為了測試本文提出MCABC 算法的性能，采用15 個標準測試函數，將MCABC與文獻［4］提出的ABC、文獻［25］提出的GABC（Gbest-guided Artificial Bee Colony）、文獻［26］提出的qABC（quick Artificial Bee Colony）、文獻［27］提出的CABC 四種算法進行比較，仿真基于Matlab 2016a 軟件平臺實現。測試函數信息如表1所示。

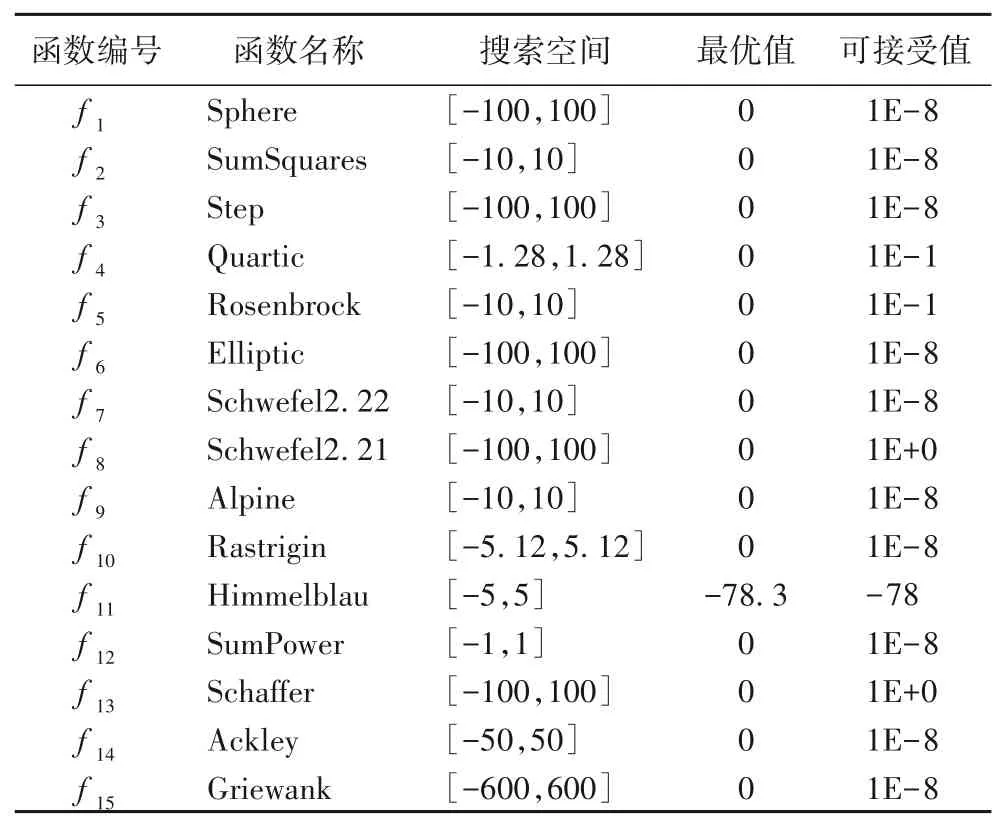
表1 標準測試函數Tab.1 Benchmark functions

仿真在一臺搭載1.6 GHz 的Intel Core i5 處理器和4 GB內存的PC 平臺上實現。考慮對算法性能進行較為全面的測試，采用的15 個測試函數包括了各種類型的特征函數，f1、f2、f4、f6～f8、f12為連續單峰函數，在解空間中僅有一個極值點；f3在特定的間隔產生階躍現象，是一種不連續的階躍函數；f5的特征與問題的維數有關，當D≤3 時，f5為單峰函數，當D>3時，f5為多峰函數；f9～f11、f13～f15為連續多峰函數，在解空間中存在大量的局部極小值點，該類函數在求解時易陷入局部最優。算法實驗參數設置如下：蜂群規模NP=60，算法最大迭代次數MCF=5000，未更新限制次數Limit=3000，為了測試算法在低維和高維條件下求解性能的差異，分別在函數為50維和100 維時進行測試。比較算法的特定參數均參照原文設定［2-3］：qABC 中r=1.5，GABC 中C=1.5。對每個測試函數運行20次，得到最優值（Best）、平均值（Mean）、方差（Std）及達到可接受值的平均迭代次數（Minc），50 維和100 維仿真結果如表2～3所示

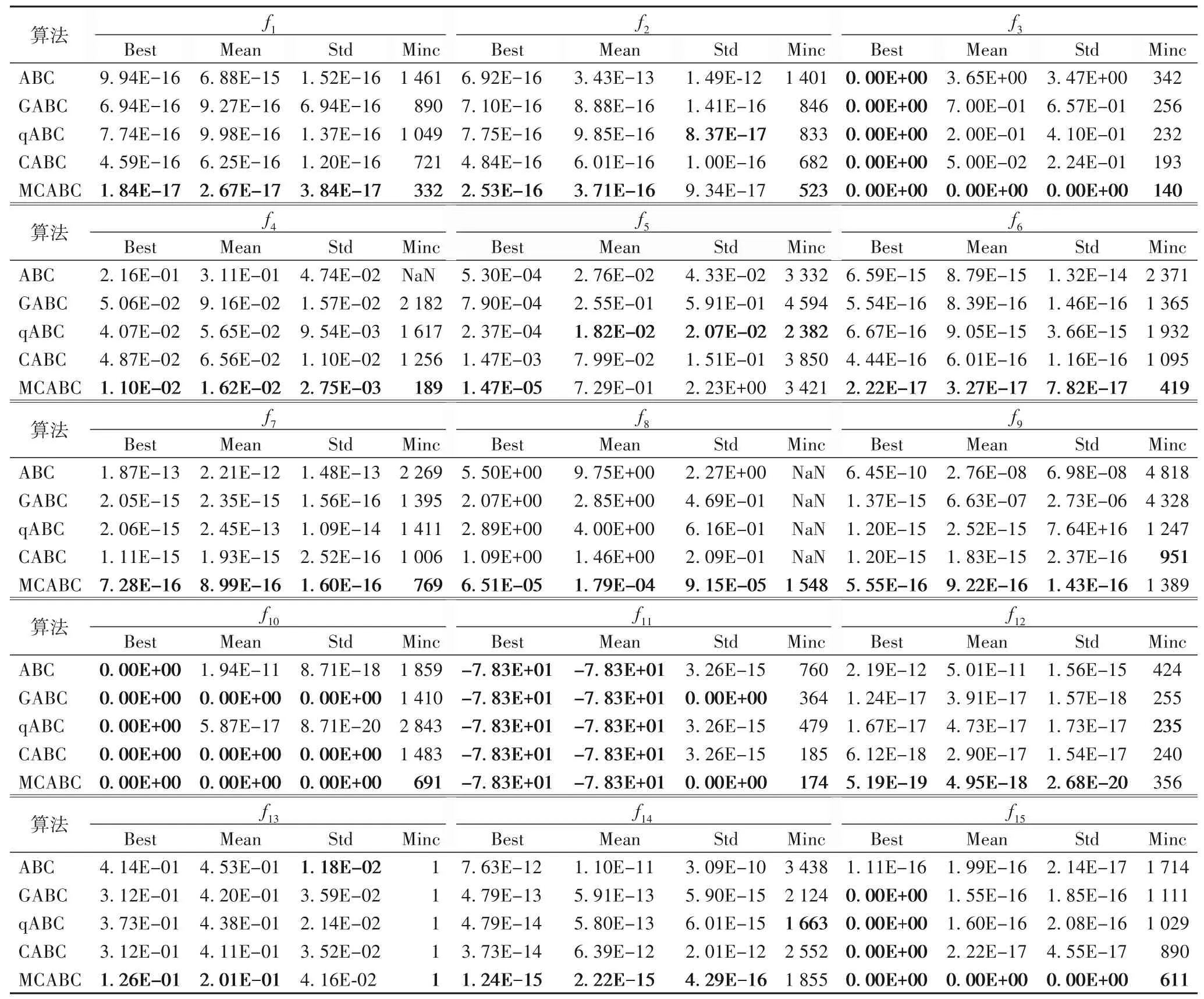
表2 低維函數下5種算法的仿真結果（D=50）Tab.2 Simulation results of five algorithms under low-dimensional functions（D=50）

本文采用4 個評價指標對各算法的性能進行對比，Best（Mean）表示20 次獨立測試中的最佳目標值（平均目標值），Std（Minc）記錄了20次獨立實驗測試結果的標準差（達到可接受值的平均迭代次數）。表2 記錄了D=50 的測試結果。與標準ABC 相比，對于除f3、f10以外的所有函數，MCABC 在收斂速度、求解精度、穩定性上均優于ABC，由于f3全局最優是一個區域，f10全局最優不是一個點，因此這兩個函數更容易搜索到最優值，所以MCABC 與ABC 都能夠求得最優值，但MCABC 在收斂性和穩定性上顯著優于ABC。此外，在函數f8、f9、f12、f15的求解中，MCABC的求解性能遠優于ABC。MCABC 與其他改進ABC 相比，在求解精度上，對于函數f3、f10、f11、f15，MCABC 與其他改進ABC 均能達到最優值，在除f3、f10、f11、f15以外的其他函數上，MCABC 在求解精度上均不同程度優于其他改進ABC。在算法穩定性上，qABC 在f5上優于MCABC，特別對于函數f10，GABC、CABC 與MCABC 均具有最強的穩定性，在函數f11的求解中，GABC 和MCABC 也具有相同的強穩定性，在除f5、f10、f11外的其他函數上，MCABC 均優于其他改進ABC。在算法收斂性上，qABC 在f5、f12、f14略優于MCABC，CABC 在f9優于MCABC，在除f5、f12、f14、f9外的其他函數上，MCABC 均遠優于其他改進ABC。綜上，在50 維函數測試條件下，MCABC的綜合尋優能力優于已有的改進ABC。

為進一步驗證本文改進算法在高位函數中的有效性，選擇文獻中常用的4 個具有代表性的測試函數在100 維條件下進行仿真，結果如表3所示。

表3 高維函數下5種算法的仿真結果（D=100）Tab.3 Simulation results of 5 algorithms under high-dimensional functions（D=100）

由于MCABC采用多維匹配和異維協同的更新機制，因此MCABC 在收斂精度上均超過其他算法，尤其是對于函數f10、f15，MCABC 盡管在穩定性上不如低維條件下好，但是依舊能收斂到理論最優。100 維測試下MCABC 相較于ABC 及其他改進算法在收斂速度上具有顯著優勢，并且在穩定性上均優于其他算法。為更加可視化展示MCABC的求解性能，選取不同類型的四個函數f1、f7、f10、f15，分別在50 維和100 維條件下對5個算法進行對比，如圖5～6所示，其中，收斂函數圖是本次獨立實驗的收斂函數曲線。

由圖5～6 可以看出，得益于搜索方程更新模式的多樣性，無論在低維還是高維測試中，MCABC 收斂速度均明顯快于其他算法，且收斂精度最高，均保持良好的下降趨勢。在50 維測試條件下，改進4 種ABC 算法能夠有效發揮各自不同的優勢，下降速度和趨勢差異較為明顯；在100 維測試條件下，由于維度的顯著增加，受限于搜索方程更新模式的單一性，削弱了改進ABC 算法各自的優勢，各改進ABC 算法的下降趨勢和收斂速度相對接近，收斂曲線差異性減小，但MCABC 仍舊保持相較于其他算法的顯著優勢。

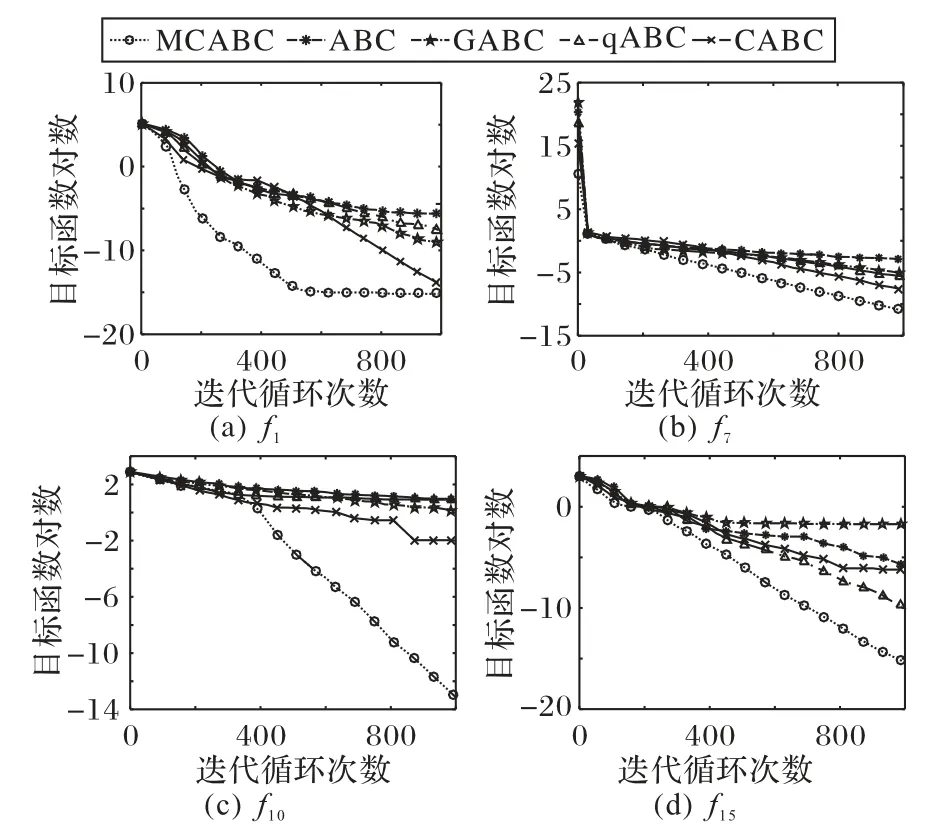
圖5 四個標準測試函數的50維收斂圖Fig.5 Fifty-dimensional convergence graph of 4 benchmark functions

圖6 四個標準測試函數的100維收斂圖Fig.6 One hundred-dimensional convergence graph of 4 benchmark functions

3.2 算法的運行時間

為了檢驗MCABC 的時間復雜度，在相同的運行環境下，計算各算法的運行時間，計算得到15個算法在D=50條件下的平均運行時間如表4 所示。由表4 可以看出，由于MCABC與ABC 的時間復雜度相差不大，故在運行時間上略有增加，而MCABC相較于其他三種比較算法在運行時間上均有降低。因此，本文提出的尋優方法在可接受的計算時間內能夠有效提高算法的求解質量。

表4 不同算法運行時間對比 單位：sTab.4 Running time comparison of different algorithms unit：s

4 結語

本文提出了一種基于多種群組合策略的人工蜂群算法，通過將多維匹配和異維協同兩種更新機制引入搜索方程，提高了算法更新模式的多樣性；同時，分別針對雇傭蜂和觀察蜂提出了兩個組合策略，以平衡算法的廣度探索和深度搜索，并在雇傭蜂階段劃分自由子集和非自由子集，以明確個體的搜索重點。通過對標準測試函數進行仿真實驗，進一步驗證了本文所提出的MCABC算法具有良好的尋優性能。