不良地質(zhì)隧道圍巖穩(wěn)定性預測模型構(gòu)建與分析

李和元，黃衛(wèi)國，胡凱

(江西省公路工程監(jiān)理有限公司，江西 南昌 330100)

監(jiān)控量測是隧道施工中實時掌握隧道變形的量測手段，如何通過監(jiān)控量測數(shù)據(jù)有效預測隧道未知變形是當今研究的熱門話題。但該方法只能監(jiān)測隧道變形實際情況，不能較準確地預測未知的隧道變形規(guī)律。灰色模型是隧道施工過程中進行變形預測的有效手段，通過對監(jiān)控量測實時數(shù)據(jù)的分析，對未知變形規(guī)律進行評估預測。宋海萍對礦區(qū)地表沉降灰色系統(tǒng)理論預測模型進行研究，認為將灰色理論應用于礦區(qū)地表沉降預測很準確；蘭澤全等進行煤礦特別重大事故灰色預測與分析，得出灰色預測有利于實時掌握煤礦地表變形情況，能準確判斷未知的變形規(guī)律；牛景太等對施工期高心墻堆石壩沉降變形監(jiān)控模型進行研究，發(fā)現(xiàn)利用灰色理論進行變形預測比監(jiān)控量測能更有效地掌握施工場地變形規(guī)律；秦擁軍等采用基于灰色關聯(lián)理論的Peck法進行隧道地表移動參數(shù)影響研究，發(fā)現(xiàn)灰色模型預測值與實際值的相對誤差較小，且精度符合施工要求；劉鵬程等采用分數(shù)階算子灰色理論對隧道圍巖變形進行了預測。利用灰色理論建立灰色模型對工程地表變形進行預測可行，且預測精度達到設計與施工要求。該文基于灰色理論建立隧道圍巖穩(wěn)定性預測模型，以某軟巖條件下不良地質(zhì)隧道為例，分析該模型預測值與實際值之間的誤差，提出合理的不良地質(zhì)隧道圍巖穩(wěn)定性預測模型。

1 灰色理論預測模型的構(gòu)建

1.1 模型構(gòu)建

隧道變形是以時間線來監(jiān)測的，故以時間線為依據(jù)建立灰色預測模型。對于所得隧道監(jiān)測變形數(shù)據(jù)，不需進行相應規(guī)律分析和概率統(tǒng)計，僅需對已知數(shù)據(jù)進行相應處理即可得到與時間序列相關的數(shù)據(jù)。隧道變形沉降監(jiān)測時間的序列為：

T(0)={T(0)(1),T(0)(2),T(0)(a-1),

T(0)(a)}

(1)

式(1)中，沉降監(jiān)測時間序列沒有規(guī)律，故按式(2)對式(1)中數(shù)據(jù)作一次累加處理，將數(shù)據(jù)序列變?yōu)橛幸?guī)律序列。

(2)

通過一次累加處理，得到隧道變形沉降監(jiān)測時間的新序列：

T(1)={T(1)(1),T(1)(2),T(1)(a-1),

T(1)(a)}

(3)

按照同樣的方法，得到隧道變形沉降監(jiān)測值的原始數(shù)據(jù)序列和新序列：

(4)

根據(jù)灰色理論，所得到的新序列服從指數(shù)分布，隧道變形沉降監(jiān)測值F與隧道變形沉降監(jiān)測時間T之間的一階線性微分方程為：

(5)

式中：A、B為灰色參數(shù)。

對式(5)進行積分求解，得：

F(T)=C·exp(A-AT)+BA-1

(6)

T=1時，有F(T)=F(1)，代入式(6)，得：

F(1)=C·exp(A-A×1)+BA-1

(7)

解得C=F(1)-BA-1。

隧道變形沉降監(jiān)測值F與隧道變形沉降監(jiān)測時間T之間的一階線性微分方程可表達為：

F(T)=(F(1)-BA-1)·exp(A-AT)+

BA-1

(8)

根據(jù)函數(shù)在導數(shù)上面的定義，可知：

(9)

要使函數(shù)能與一次累加的新序列聯(lián)系上，只需使ΔT→1即可。將ΔT→1代入式(9)，得：

(10)

由于一階線性微分函數(shù)是連續(xù)的，ΔT較小時，函數(shù)值不可能出現(xiàn)較大波動。因此，要得到較合理的隧道變形沉降監(jiān)測值F，只需取F(T)和F(T+1)的平均值即可。將該平均值代入式(5)，得：

F(0)(T+1)=B-0.5A[F(1)(T)+

F(1)(T+1)]

(11)

基于上述推導，當T=1，2，…，a-1，a時，代入式(11)，得：

(12)

將式(12)用矩陣方式表達，并進行簡化，得：

(13)

令：

式(13)可寫為：

F=F*D

根據(jù)最小二乘法，得：

(14)

式(14)即為灰色參數(shù)的計算式。隧道大變形預測的函數(shù)表達式為：

exp{-A[T(1)(i+1)-T(1)(1)]}+BA-1

(15)

式中：i=1，2，…，a-1，a。

1.2 灰色理論預測模型驗算

隧道變形沉降監(jiān)測值F原始數(shù)據(jù)的平均值為：

隧道變形沉降監(jiān)測值F原始數(shù)據(jù)的方差為：

1.2.1 殘差驗算

由于灰色理論的構(gòu)建是按照相應序列開展的，殘差驗算也需要先設定相應樣本數(shù)據(jù)的殘差序列ω(0)(i)：

殘差序列ω(0)(i)的平均值為：

殘差序列ω(0)(i)的方差值為：

引入方差比ν和誤差概率P：

式中：SF和Sω(0)為隧道變形沉降監(jiān)測值F原始數(shù)據(jù)的方差值和殘差序列ω(0)(i)的均方差。

方差比ν和誤差概率P對于灰色理論預測模型精度的評價標準見表1。

表1 殘差對灰色理論預測模型精度的分級標準

1.2.2 關聯(lián)度驗算

通過計算預測值與實測值之間關聯(lián)性大小判斷灰色理論預測模型的精度。假定：

引入關聯(lián)系數(shù)ξ(i)，其表達式如下：

ξ(i)=

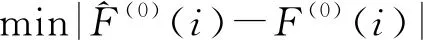
關聯(lián)度R是結(jié)合方差比ν和誤差概率P對灰色理論預測模型精度進行的綜合評價，計算公式見式(16)，評價標準見表2。

表2 關聯(lián)度對灰色理論預測模型精度的分級標準

(16)

1.2.3 后驗差驗算

后驗差驗算是基于殘差驗算開展的，其計算方式及等級評價標準與殘差驗算一樣，不再贅述。

2 算例分析

十房(十堰—房縣)高速公路通省隧道為分離式隧道，全長6.887 km，采用設計速度80 km/h雙向四車道標準建設。該隧道穿越絹云母片巖地層，是國內(nèi)規(guī)模最大的變質(zhì)軟巖隧道，存在軟巖大變形、突泥涌水等不良地質(zhì)。表3為其拱頂沉降監(jiān)測數(shù)據(jù)。通過上述灰色理論預測模型預測其拱頂沉降，并與實測值進行對比分析。

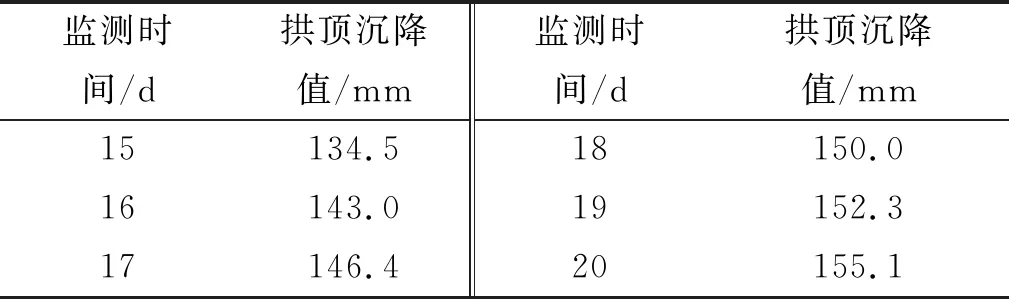
表3 通省隧道拱頂沉降監(jiān)測數(shù)據(jù)

根據(jù)表3，隧道拱頂沉降監(jiān)測時間序列如下：

F(0)=(F(0)(1),F(0)(2),F(0)(3),F(0)(4),F(0)(5),

F(0)(6))=(134.5,143.0,146.4,150.0,

152.3,155.1)

對F(0)作一次累加，得到新的序列：

F(1)=(F(1)(1),F(1)(2),F(1)(3),F(1)(4),F(1)(5),

F(1)(6))=(134.5,277.5,423.9,573.9,

726.2,881.3)

對序列F(1)作緊鄰均值生成，將數(shù)據(jù)代入式(13)，得：

f(1)(i)=(f(1)(2),f(1)(3),f(1)(4),f(1)(5),

f(1)(6))=(206,350.7,498.9,650.05,

803.75)

則有：

將F和F*代入式(14)，得：

將計算得到的A和B代入式(5)，得：

將上述數(shù)據(jù)代入式(15)，得到隧道變形預測模型如下：

4 581.102 07

(17)

由式(17)可知：

F(1)(5),F(1)(6))=(134.5,279.91,429.8,

584.32,743.60,907.79)

累減生成新序列：

159.28,164.19)

原本的序列為：

F(0)(i)=(134.5,143.0,146.4,150.0,152.3,

155.1)

將上述數(shù)據(jù)代入公式，得到隧道變形預測結(jié)果(見表4)，預測結(jié)果與實測值的對比見圖1。

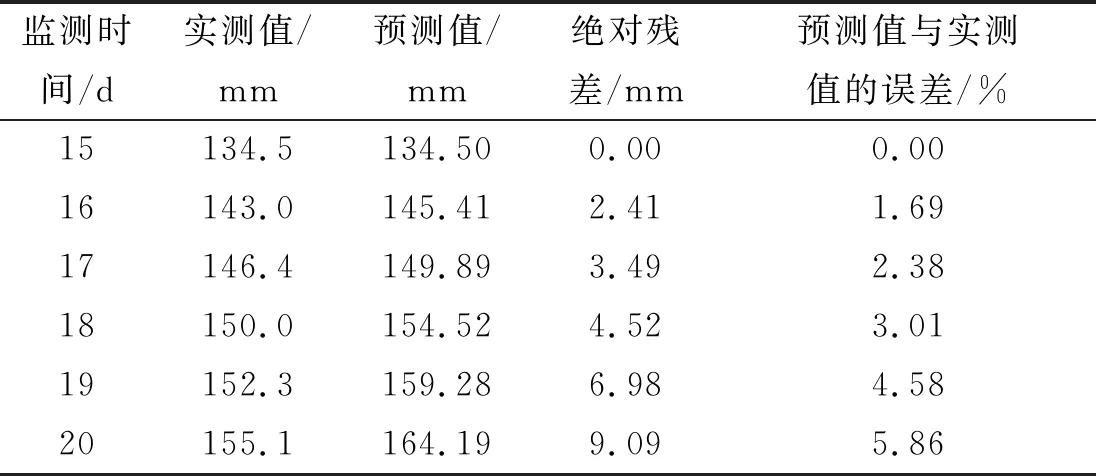
表4 隧道拱頂沉降監(jiān)測數(shù)據(jù)與預測數(shù)據(jù)對比

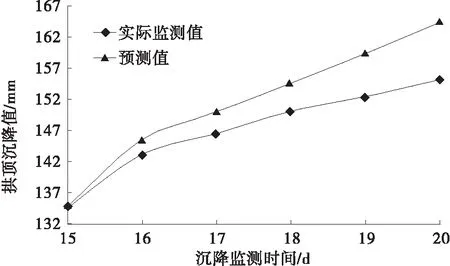
圖1 隧道變形預測結(jié)果與實測值對比

由表4和圖1可知：對15～20 d隧道拱頂變形實測值和預測值的最大誤差為5.86%，最小誤差為零，模型精度符合要求；隨著拱頂沉降監(jiān)測時間的增加，拱頂沉降預測數(shù)據(jù)與實測數(shù)據(jù)間的相對誤差雖然在可接受范圍內(nèi)，但誤差越來越大。

3 結(jié)論

(1)隧道拱頂變形隨著時間的增加而增大。灰色預測模型的最大誤差為5.86%，最小誤差幾乎為零，模型精度滿足要求。

(2)利用灰色理論構(gòu)建預測模型，隨著隧道拱頂沉降監(jiān)測時間的增加，拱頂變形預測數(shù)據(jù)與實測數(shù)據(jù)的相對誤差雖在允許范圍內(nèi)，但誤差越來越大。