用P波初動資料確定地震震源機制教程（二）

陳運泰 劉瑞豐

1）中國北京 100049 中國科學院大學地球與行星科學學院

2）中國北京 100081 中國地震局地球物理研究所

2 斷層和破裂

2.1 破裂的最大剪切應力理論

1773 年，庫侖（Coulomb，Charles Augustine，1736—1806）提出破裂的最大剪切應力理論（Coulomb，1785；Jeffreys，1942，1976）.他假設，在應力作用下，當脆性物質（例如巖石）中某一點的最大剪切應力達到某一確定值時，就沿著最大剪切應力平面破裂。通常把這個值稱為該物質的剪切強度（shear strength）.

1849 年，霍普金斯（Hopkins）根據庫侖提出的準則，證明了破裂平面（即最大剪切應力平面）是通過中間主應力軸并平分最大與最小主應力軸之間的夾角的平面，而作用于此平面上的剪切應力（最大剪切應力）等于最大與最小主應力之差的一半.通常，把最大主應力與最小主應力之差稱為應力差（stress-difference）.應力差總為正值.

以p1,p2,p3代表脆性物質（例如巖石）中某一點的主應力[圖12（a）].若使用以主應力的方向為直角坐標系xi（i=1，2，3）的坐標軸的方向，過某一點取一個xi為常數的平面，按彈性理論與地震學通常的習慣（Bullen，1953；Jeffreys，1976），那么應力分量pik表示的是作用于該平面兩側的物質之間單位面積上，并使xi較小一側的物質朝xk增大方向位移的力.因此，若按照彈性理論與地震學通常的習慣，主應力以張應力為正.不過，在把理論分析結果應用于地學問題，特別是巖石力學、土力學、構造地質學時，考慮到所涉及的正應力以壓應力為主，則通常把符號的規定反過來，以壓應力為正（Jaeger，1962；Jeffreys，1976；Jaeger and Cook，1979；Atkinson，1987；Turcotte and Shubert，2001）.在以下分析中，為避免混淆，除非特別說明，均按彈性理論與地震學通常的習慣，以張應力為正.

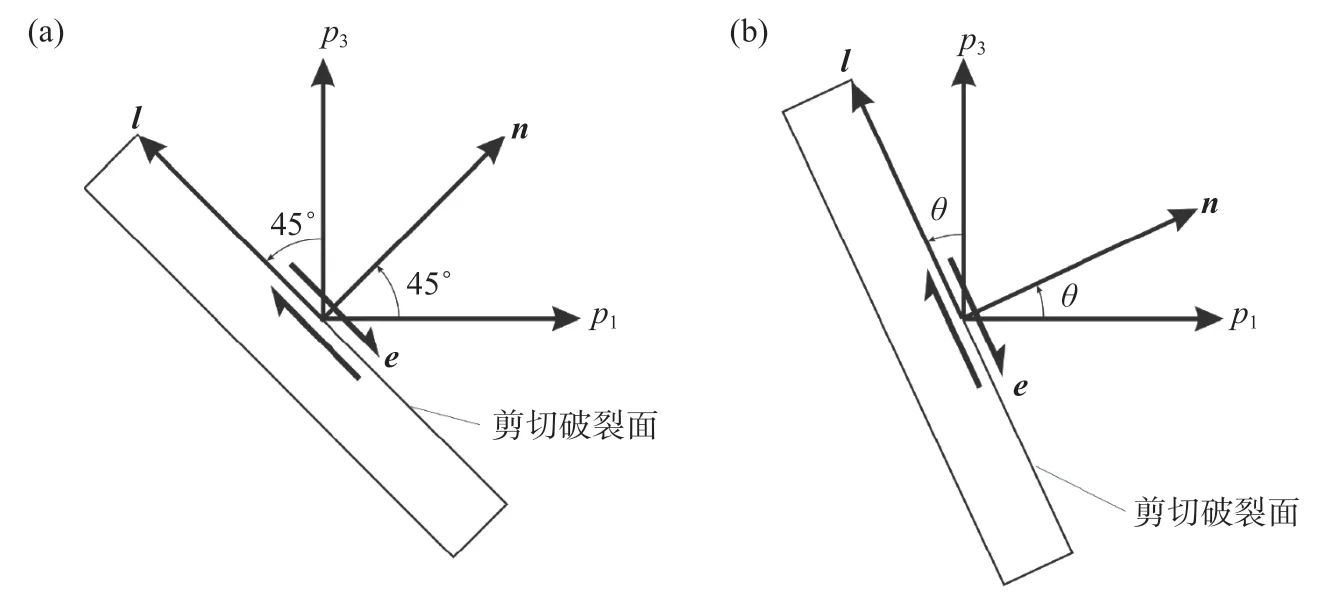
圖12 最小主壓應力軸（p1）、最大主壓應力軸（p3）、破裂面法線方向（n）、滑動方向（e）和剪切破裂面之間的幾何關系（a）破裂的最大剪切應力理論；（b）安德遜理論Fig.12 Minimum principal compressive stress axis（p1），maximum principal compressive stress axis（p3），normal direction of fracture surface（n），geometric relationship between slip direction（e）and shear fracture surface（a）Maximum shear stress theory of fracture;（b）Anderson theory

設p1＞p2＞p3，也就是說，p1,p2,p3依次是最大、中間、最小主（張）應力軸.與主應力p1,p2,p3的方向相應的x1,x2,x3軸的方向依次稱為最大、中間、最小主（張）應力軸方向.若按巖石力學的規定，則p1,p2,p3依次是最小、中間、最大主（壓）應力軸.與p1,p2,p3軸相應的方向依次稱為最小、中間、最大主（壓）應力軸方向.

今以ni（i=1，2，3）表示某一平面的法線n的方向余弦，以li和mi分別表示該平面上兩條互相垂直的直線l和m的方向余弦.以l，m，n構成一個右旋直角坐標系，即以朝外的法線方向n的左方為l的正方向，那么作用于該法線方向n的平面的應力矢量（stressvector traction）pn為

pn的法向分量即作用在該平面上的法向應力pnn，則有

而剪切應力在l和m方向的分量分別為pnl和pnm，則有

在該平面內與l和m的夾角分別為?和?－（π/2）的方向上，剪切應力為

該剪切應力在

時達極大值，其數值p為

由式（13）及式（9）與式（10）容易求得作用于該平面的最大剪切應力的數值p.為書寫簡單起見，給出該數值p的平方，則有

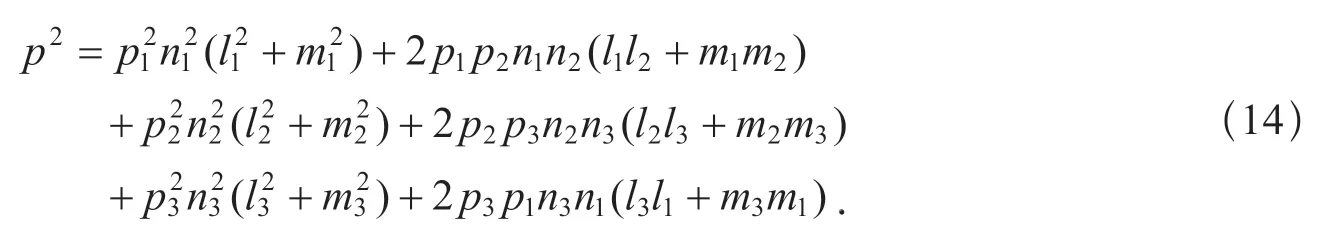
因為（l1，m1，n1），（l2，m2，n2），（l3，m3，n3）分別為p1，p2，p3軸在l，m，n坐標系中的方向余弦，所以

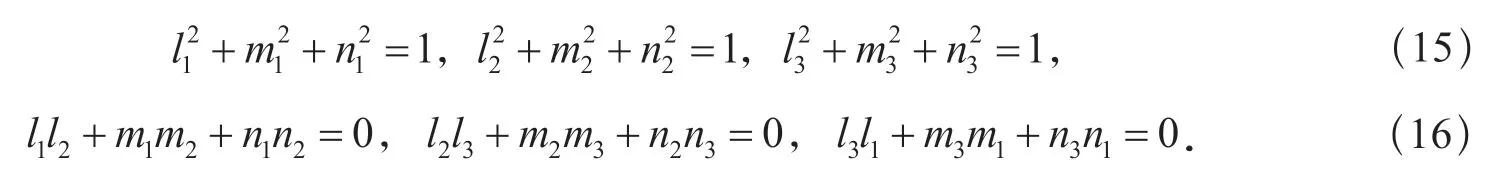
利用這些關系式，可將p2表示為

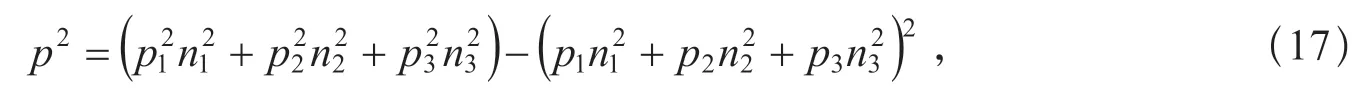
即

注意到

則容易將p2表示成

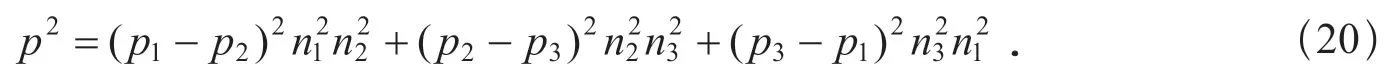
欲求最大剪切應力所在平面的法線方向n，就是要求在

所限制的條件下p2的極大值.采用拉格朗日乘子法求p2取極大值的必要條件.為此，引進一個新的參量，即拉格朗日乘子λ，并定義一個新的函數F，有

由于g≡ 0，所以F取極值的條件也就是p2取極值的條件，這些條件是

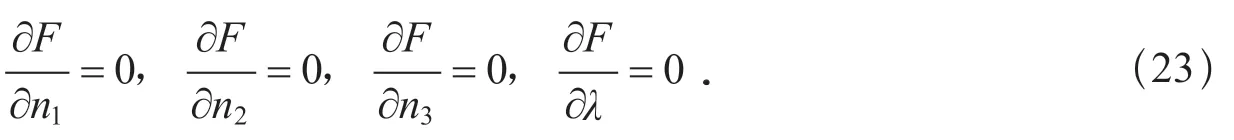
由這些條件可以決定n1，n2，n3和λ.將式（17）代入式（23），由式（23）的最后一個條件給出式（21），其余三個可以表示為

式中，n1，n2，n3至少有一個應當等于零，如其不然，則p1，p2，p3應滿足同一個二次方程

然而二次方程至多只能有兩個不等的根，而不可能有三個不等的根p1，p2，p3.這就導致了與p1＞p2＞p3的假設相矛盾的結論.因此，n1，n2，n3中至少有一個等于零，也就是說，最大剪切應力平面應當通過某一主應力軸.

如果最大剪切應力平面通過p2軸，即n2=0，而n1，n3≠0，那么由式（24）的第一與第三式可得

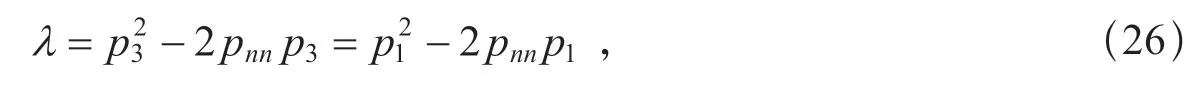
因此

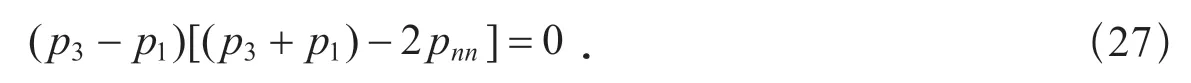
既然p3≠p1，則有

將式（28）中的pnn用式（8）代入，可得

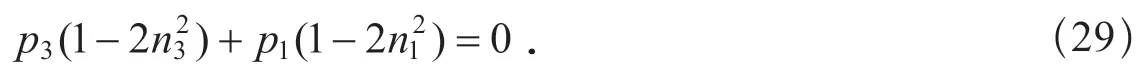
由式（19）可知，當n2=0 時

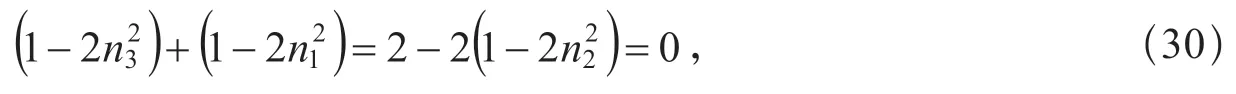
則式（29）便簡化為

再次運用p3≠p1的條件，可得

把n2=0，=1/2代入式（19），則得到p2的最大值.

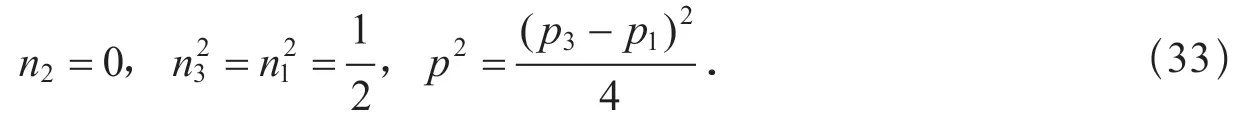
若依次設n3=0 及n1=0，那么按照類似的步驟可以求得

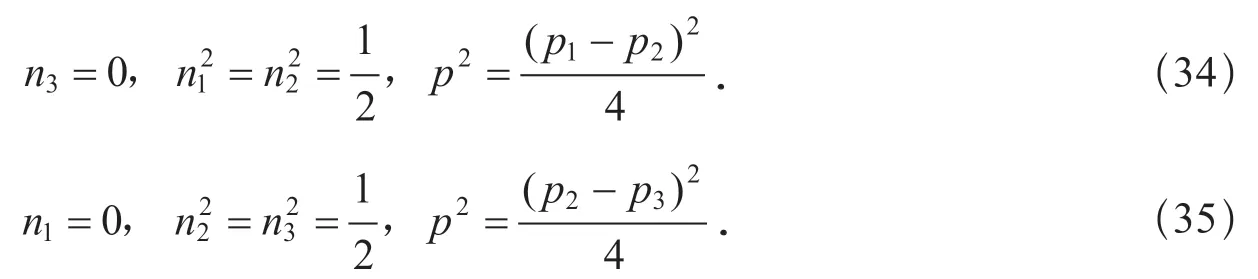
既然p1＞p2＞p3，所以只有式（33）給出的p才是數值最大的剪切應力值.最大剪切應力平面的法向是

如式（17）,（20）,（32）,（36）諸式所表示的，n對于p1和p3軸均具有對稱性，因此只需分析

一種情形.此時，若取

則由式（8）—（10）可得

這就是說，最大剪切應力平面通過中間主應力軸并平分最大與最小主應力軸之間的夾角.最大剪切應力的數值是最大與最小主應力之差的一半，其作用方向在垂直于中等主應力軸并且位于剪切平面內的－l方向[圖12（a）].

既然n對于p1和p3軸有對稱性，則另一種情形（以p3軸為對稱軸的情形）是

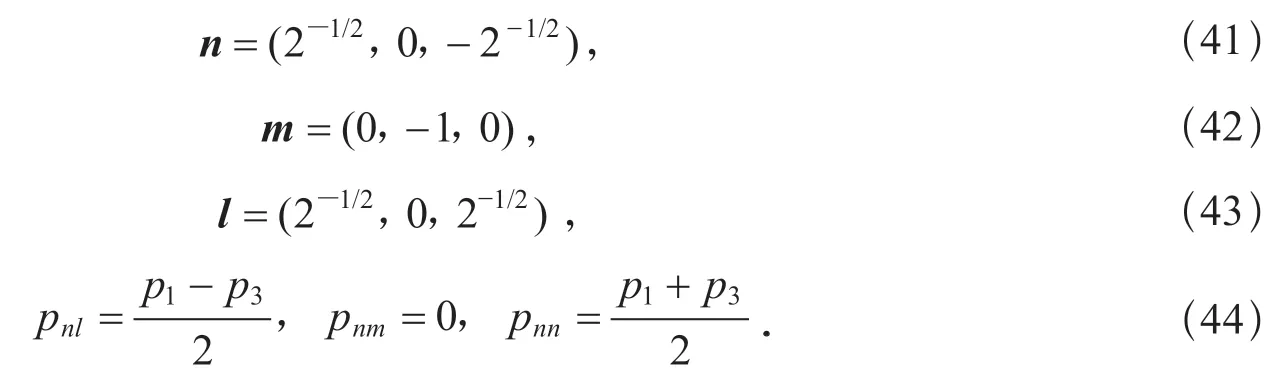
上式所表示的結果即是與式（37）—（40）所表示的結果共軛的情形.其他2 種情形，即n=（-2-1/2，0，-2-1/2）與n=（-2-1/2，0，2-1/2）情形則分別與式（37）與式（41）給出的情形相同.

上述脆性破裂的最大剪切應力理論稱為庫侖—霍普金斯理論.

2.2 安德遜理論

實驗證明，在單軸壓力下，脆性物質的破裂與庫侖—霍普金斯理論預期的結果相符，p3軸與破裂面之間的夾角約為45°.地震是地表面下巖石的破裂，在地質條件下，地表面下的巖石承受著其上方巖石重量引起的沉重的載荷，也即高圍壓，稱為靜巖壓（lithostatic pressure）.許多證據表明，在高圍壓下，上述角度可減至20°—30°.為解釋這一現象，安德遜（Anderson，1905，1942，1951）將庫侖—霍普金斯的理論加以修正，他運用了庫侖關于巖石脆性破裂的準則[圖12（b）].庫侖準則亦稱庫侖—納維（Navier）準則、納維—庫侖準則、庫侖—莫爾（Mohr）準則，但后三者與前者所涉及的物理背景實際上并不相同，因此這里仍稱之為庫侖準則（Jaeger，1962；Jaeger and Cook，1979）.

按照庫侖準則，巖石要發生破裂，產生滑移，除了要克服表征材料特征的內聚力以外，還要克服與法向壓應力（|pnn|）成正比的固體摩擦力的阻礙.因此，只有當作用于巖石中某一個面上的剪切應力達到剪切強度，即內聚強度（cohesive strength）S和摩擦阻抗（μi|pnn|）之和時，巖石才能沿著該平面發生脆性破裂，也就是

式中，μi是內摩擦系數（coefficient of internal friction）.地殼中大部分，特別是地殼上部都有流體（主要是水）存在.水和其他流體的存在影響斷層的摩擦滑動.在濕斷層情況下，式（45）中的壓應力|pnn|應改為有效正應力（effective normal stress），即破裂面上壓應力|pnn|與孔隙壓（pore pressure）pf的數值|pf|之差.孔隙壓即孔隙中的流體對斷層的壓強.因此

以水為例.如果孔隙中的流體（水）與地表面是自由地連通的，且無流動耗損，則孔隙壓即靜水壓，有

式中，ρf是流體（水）的密度，g是重力加速度，h是斷層所在的深度.設巖石的平均密度是ρ，則巖石重量引起的載荷即靜巖壓，有

因為水的密度比巖石的密度小得多，所以靜水壓一般只是靜巖壓的35%至50%.但是，在某些情況下，例如當水處于圈閉狀態時，孔隙壓可能幾乎等于甚而大于靜巖壓.此時，阻止斷層運動的剪切應力很小.

若pnn是壓力，|pnn|=-pnn；若pnn是張力，|pnn|=pnn.所以，在干摩擦情況下，有

在上式以及以下的討論中，上、下方的符號（在上式中是+號）分別對應pnn是壓力或張力的情形.在干摩擦情況下，為了求破裂平面的法向n，需要求在式（21）所限制的條件下|p|±μipnn這個量的極大值，在這里以及以下的討論中，±號分別對應pnn是壓力或張力的情形.與上節類似，定義一個新的函數Φ，則

式中，λ是拉格朗日乘子，g仍如式（21）所示.由于g≡ 0，所以Φ取極值的條件也就是|p|±μi pnn取極值的條件，這些條件是

上式表示的最后一個條件仍給出式（21），其余三個條件可以表示為

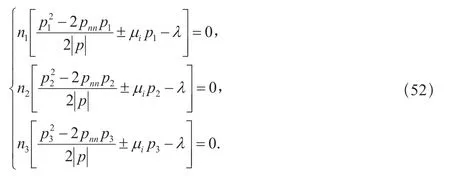
與前面討論庫侖—霍普金斯理論的情況類似，n1,n2,n3應當至少有一個等于零.若設n2=0，而n3,n1≠0，則由上式的第一與第三式可得

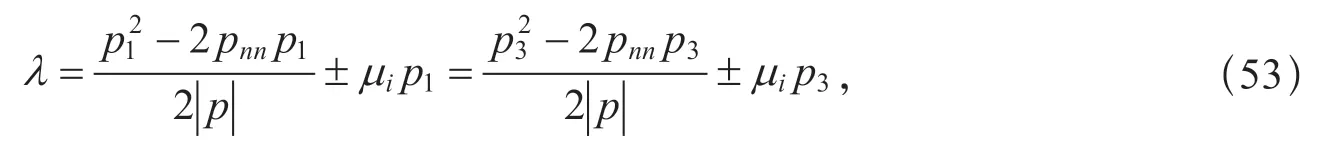
因此

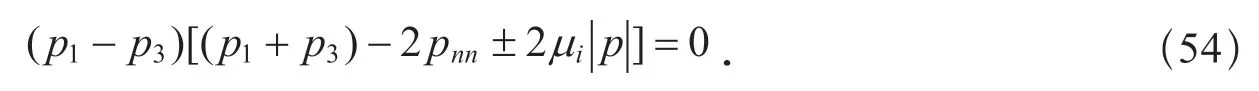
因為p1≠p3，所以

將式（8）和式（19）代入上式，可得

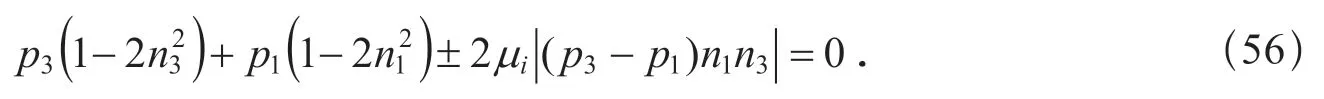
今以θ表示n與p1軸的夾角，即n與最大主（張）應力軸（p1軸）的夾角（Scholz，1990，2002）.則

按這里采用的定義，在式（45）—（56）的分析中，只涉及剪切應力的數值|p|，因此在式（56）中，改變n1或（和）n3的符號，該式照樣成立.換句話說，n對于p1，p3軸都是對稱的.由于n對于p1和p3軸的對稱性，只需求0 ≤θ≤90°的解.因此，式（56）可以表示為

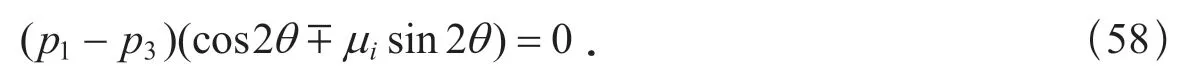
因為p1≠p3，所以

這就是說，當pnn是壓應力即上式右邊取正號時，有

而當pnn是張應力即式（59）右邊取負號時，有

此時，|p|±μipnn達極大值，也就是

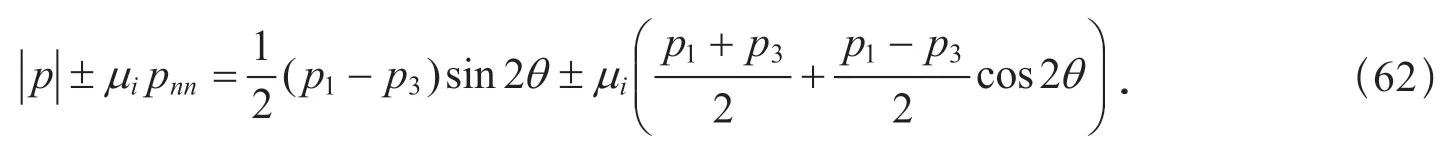
由式（59）可得

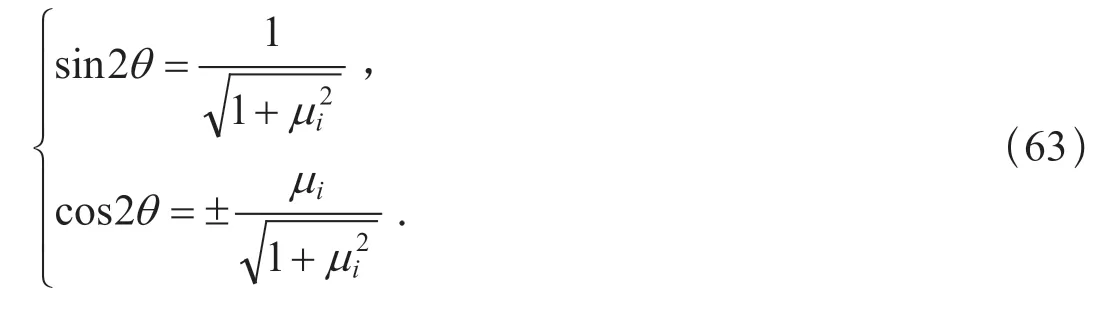
無論pnn是壓應力還是張應力，sin2θ均由上式第一式表示，而上式第二式的±分別對應于pnn是壓應力與張應力情形.所以

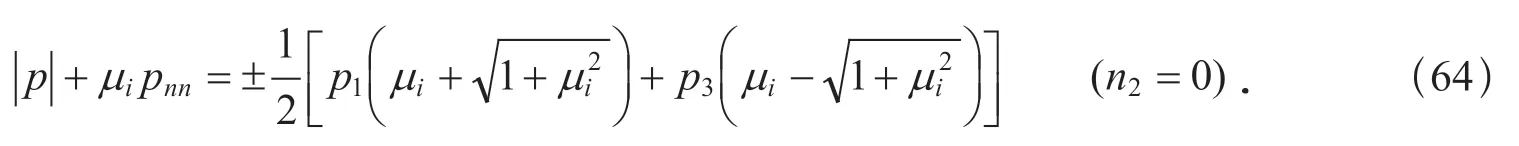
對于n3=0 和n1=0 的情形，可以作類似的討論.在這兩種情形下，若以θ依次表示n與p2和n與p3軸的夾角，可以求得

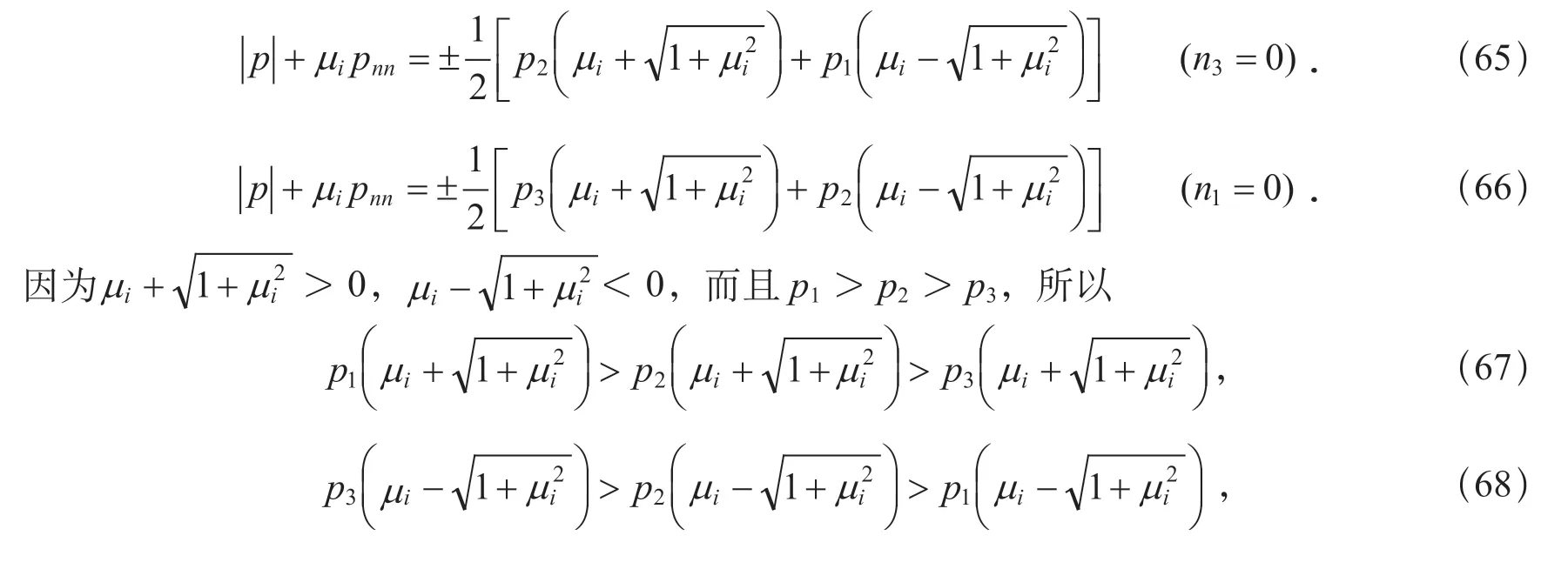
這就證明了無論pnn是壓應力還是張應力情形，以

為法向的平面是欲求的剪切破裂面.θ由式（60）（當pnn是壓應力時）或式（61）（當pnn是張應力時）給出.θ是破裂面法向n與最大主（張）應力軸（p1軸即最小主壓應力軸）的夾角，也是剪切破裂面與最小主（張）應力軸（p3軸即最大主壓應力軸）的夾角.當μi=0 時，θ=π/4；當μi=1 時，θ=π/8（pnn是壓應力情形）或3π/8（pnn是張應力情形）；當μi→∞時，θ=0（pnn是壓應力情形）或π/2（pnn是張應力情形）.這就是說，隨著μi的增大，對于pnn是壓應力情形，剪切破裂面的法向趨向最大主（張）應力軸，剪切破裂面趨向最小主（張）應力軸（p3軸，即最大主壓應力軸）與中間主應力軸（p2軸）構成的平面.這是很自然的.在pnn是壓應力情形，壓應力起著增加對剪切破裂的阻抗作用，因此剪切破裂在主（壓）應力軸與破裂面的夾角變小、剪切應力增加的情況下發生；而在pnn是張應力情形，張應力起著減小對剪切破裂的阻抗作用，因此剪切破裂在主（壓）應力軸與破裂面的夾角變大、剪切應力減小的情況下發生.今取

則由式（8）—（10）可得

這就是說，剪切破裂面是通過中間主應力軸并與最小主（張）應力軸（p3軸）成θ角的平面，在該平面上剪切應力的數值為（1/2）（p1-p3）sin2θ，其作用方向在-l方向.圖12（b）表示了p1,p3軸，n,滑動方向e和破裂面之間的幾何關系.若以σ1＞σ2＞σ3依次表示最大、中間與最小主壓應力軸，則由于n對于σ1軸和σ3軸都有對稱性，所以有兩個可能的破裂面，它們都與σ1軸成θ的夾角.

破裂的安德遜理論與地質條件下地表面下巖石的破裂是相符的.這是因為：破裂一旦開始便是不連續的運動.如果在張力的作用下發生破裂，巖石的塊體彼此脫離分開，便無從發生摩擦.如果巖石的塊體不彼此脫離分開，只要巖石塊體相對滑移繼續進行，則摩擦力將成為巖石塊體相對滑移的主要阻力.因此，庫侖—霍普金斯理論適用于滑移起始時，而安德遜的理論則可正確地決定滑移開始后的方向.

有許多證據表明，深源地震也是巖石的破裂.如果真是這樣，式（49）中的內摩擦系數μi一定隨深度急遽地減小.而根據式（60），θ就應趨于π/4，即破裂面與主應力方向成45°角.任何有關因體積變化而發生深源地震的假說都應符合極端應力近乎水平并且破裂面與豎直方向成45°角的結果.

2.3 地震斷層

在常溫下，若應力足夠高，巖石將發生脆性破裂.在地球表面的巖石中，可以看到許多類型的破裂.如果沿破裂面發生側向位移，那么這個破裂就稱為斷層.在地殼中有著各種尺度的斷層，尺度小的斷層錯距僅幾毫米；尺度大的斷層有著由破碎了的巖石構成的寬闊地帶，稱為斷層泥帶，斷層泥帶的寬度可達數千米，而斷層的錯距可達數百千米；規模較小的斷層的斷層泥帶寬度只有幾厘米.地震與許多斷層的錯動有關，大地震的斷層位錯數量級為10 m，最大可達數10 m.

剛性板塊的相對運動通過大斷層得到調整.在海溝，海洋巖石層板塊沿下傾的斷層面俯沖到鄰接的海洋或大陸巖石層板塊下，兩大板塊的匯聚導致了俯沖作用以及世界上頻繁發生的絕大多數的大地震.通過這些規則地發生的地震，連續的俯沖過程得到了調整.但這些斷層的地面形跡在海溝底部，比較難以進行詳細的實地考察.在發散帶，在大洋中脊邊緣，有許多正斷層（normal fault）.因為在大洋中脊，巖石層很薄，所以由此導致的地震就比較小.洋脊系中的分段的洋脊是通過轉換斷層連接起來的.在轉換斷層上，發生了黏滑作用.轉換斷層在陸地上常有出露，所以研究得比較多.在大陸板塊碰撞地帶，上述三種情形的斷層都會出現.我國大陸內部的許多大地震與印度板塊和歐亞板塊的碰撞所發生的大范圍的形變地帶有關；土耳其強震活動也與這個碰撞帶往西延續有關.在大陸板塊碰撞地帶，俯沖帶以及轉換斷層，地震的頻度高、強度大.在板塊內部，也發生大地震，不過頻度低一些.

由上述情況可知，有三種基本類型的斷層：逆斷層（reverse fault），走滑斷層（strikeslip fault）和正斷層（normal fault）.這三種斷層的發生是由主應力軸在空間的取向決定的（Jaeger，1962；Jaeger and Cook，1979；Turcotte and Schubert，2001）.

2.3.1 逆斷層.如果p1軸垂直于地面，p2和p3軸平行于地面，則破裂面過p2軸并與p3軸成θ角，0°＜θ＜45°，這種斷層稱為逆斷層，也稱為逆滑斷層（reverse-slip fault）或壓性斷層（compressional fault）.如圖13（a）所示，有兩個斷層面共軛的逆斷層，其斷層面的傾角δ都等于θ.斷層面的傾角的取值范圍是0°≤δ≤45°.隨著摩擦系數由零開始增加，δ由45°逐漸減小（圖14）.

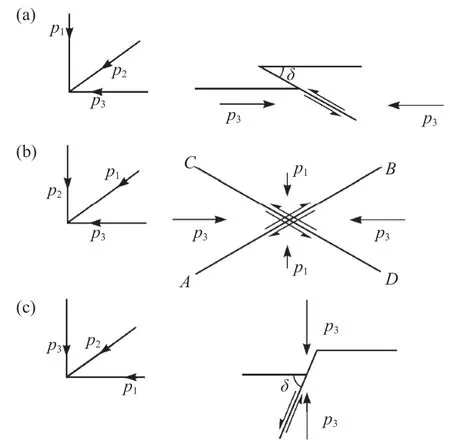
圖13 地震斷層（a）逆斷層；（b）走滑斷層；（c）正斷層Fig.13 Earthquake faults（a）Reverse fault；（b）Strike slip fault；（c）Normal fault

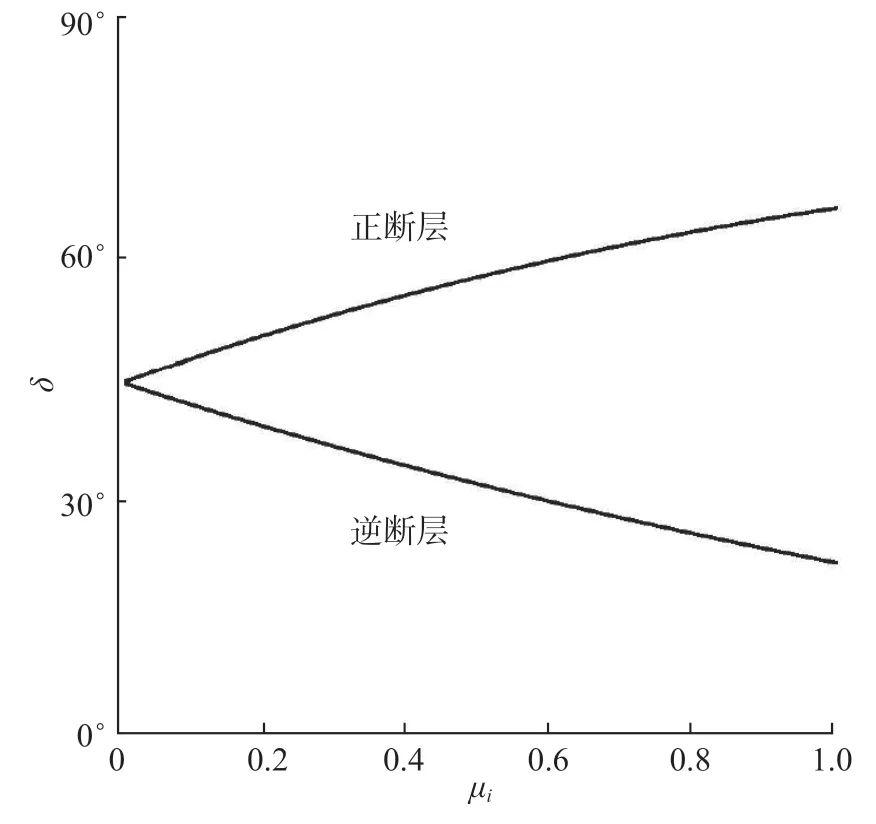
圖14 正斷層和逆斷層的斷層面傾角δ 與內摩擦系數μi 的關系Fig.14 Relationship between dip angle δ of fault plane and internal friction coefficient μi of normal fault and reverse fault

為了確定內摩擦系數μi，不但在野外對地質斷層做了許多觀測，而且在實驗室內對各種巖石做了測量（Byerlee，1967，1968，1977，1978）.結果表明，μi是數量級為1 的量，通常介于0.5 和1.0 之間.圖15 是各種不同類型的巖石開始摩擦滑動時的最大剪切應力p與正應力|pnn| 的關系圖，除了一些表示滑動面之間充塞著斷層泥的巖石的數據點外，結果比較集中：當正應力低于相當于地殼中部深度的正應力數值200 MPa（2 kbar）即|pnn|＜200 MPa 時，有

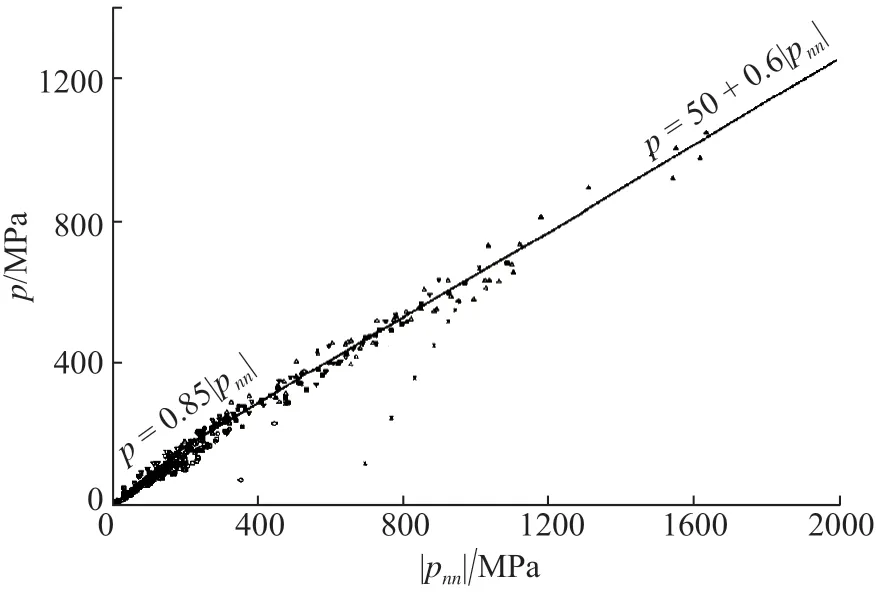
圖15 各種不同類型的巖石開始摩擦滑動時的最大剪切應力（p）與正應力（|pnn|）的關系Fig.15 The relationship between the maximum shear stress（p）and the normal stress（| pnn |）at the beginning of frictional sliding of different types of rocks

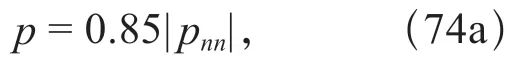
當200 MPa ＜ |pnn| ＜ 1 700 MPa 時，有

上式稱為拜爾理定律（Byerlee，1978）.在這個公式中，最大剪切應力p和正應力的數值|pnn|均以MPa 為單位，1 MPa=10 bar.若以kbar 為單位，則式（74b）等號右邊第一項的常數應改為0.5.對于式（74a）所表示的μi=0.85的情形，逆斷層的傾角δ=24.8°；對于式（74b）所表示的μi=0.6 的情形，逆斷層的傾角δ=29.5°。

2.3.2 走滑斷層.如果p2軸垂直于地面，p3與p1軸平行于地面，則圖13（b）所示的兩個共軛的斷層面都與p3軸成θ角.這種斷層稱為走滑斷層（strike-slip fault），也稱為橫推斷層（transcurrent fault）、橫斷層（lateral fault）、捩斷層（tear fault）或扭斷層（wrench fault）.走滑斷層的傾角δ常接近于90°.對于走滑斷層情形，p1可以是數值比p2和p3都小的壓應力，也可以是張應力.

走滑斷層分為右旋走滑斷層（dextral strike-slip fault，right-lateral slip fault）和左旋走滑斷層（sinistral strike-slip fault，left-lateral slip fault）.走滑斷層是右旋還是左旋可以用下述方法判別：站在斷層的一盤沿著與斷層走向垂直的方向觀看另一盤的運動，若該盤向右運動則斷層為右旋走滑斷層[圖13（b）右圖中的斷層AB]，若該盤向左運動則斷層為左旋走滑斷層[圖13（b）右圖中的斷層CD].

2.3.3 正斷層.在地下某一深度處，豎直方向的主應力可能變成最大主壓應力，即最小主（張）應力軸（p3）軸垂直于地面.此時，破裂面與垂線的夾角等于θ[圖13（c）].這種斷層稱為正斷層，也稱為正滑斷層（normal fault），張性斷層（tensional fault）或重力斷層（gravity fault）.如圖13（c）所示，正斷層的斷層面的傾角δ=90°-θ，其取值范圍為45°＜δ＜90°.隨著內摩擦系數由零增加，δ由45°逐漸增加.若μi=0.85，正斷層的傾角δ=65.2°，逆斷層的傾角δ=24.8°；若μ=0.6，正斷層的傾角δ=60.5°，逆斷層的傾角δ=29.5°.正斷層和逆斷層統稱傾滑斷層（dip-slip fault）.由于正斷層的斷層面的傾角δ=90°-θ，而因為0°＜θ＜ 45°，所以45°＜δ＜ 90°；而逆斷層的斷層面的傾角δ=θ，0°＜δ＜ 45°，所以正斷層的斷層面要比逆斷層的陡峭[圖13（a），（c）及圖14].傾滑斷層是正斷層還是逆斷層是由斷層面上方的地塊即上盤（hanging wall block）相對于下方的地塊即下盤（foot wall block）的運動是向下[圖13（c）]還是向上[圖13（a）]確定.

2.3.4 斜滑斷層.實際情況要比上述三種情形復雜，一般的斷層兼有走滑和傾滑兩種分量（圖16）.如果斷層面上的走向滑動和傾向滑動的分量都很明顯，則稱這種斷層為斜向滑動斷層（oblique fault），簡稱斜滑斷層，相應的滑動稱為斜滑（oblique slip）.斷層面兩側的地塊的運動可以用滑動矢量e描述.滑動矢量是表示斷層的上盤相對于下盤的運動方向的單位矢量.對于剪切滑動來說，滑動矢量可以位于斷層面上的任何方向上。滑動矢量與斷層面走向的夾角λ稱為滑動角（slip angle 或rake angle，分別簡稱為slip 或rake）。斷層面走向（strike）是斷層面與地面的交線，它有兩個方向，相差180°。為明確起見，規定選取站在上盤向右看的方向為斷層面走向。這樣一來，斷層面的傾向（dip direction）比斷層面的走向恒大90°，一旦說明了斷層面的走向?，0°≤?＜360°，便意味著斷層面的傾向是?+90°。當傾角δ=90°時，斷層面的走向以及上盤與下盤的選取原則上是任意的。但是，為明確起見，規定先任選兩個方向中的一個方向為斷層面的走向，一旦選定，便以沿該方向朝前看時右手邊的那一盤為“上盤”。規定0°≤λ＜360°，逆 時 針 為 正（Ben-Menahem and Singh，1981，p.183）。有 的 作 者（Aki and Richards，1980，p.106；Lay and Wallace，1995）則規定-180°＜λ≤180°，顯然，這兩種規定并無本質差別。隨著λ由0°逆時針增至360°，相應的剪切滑動斷層的地質學術語如表1 所示。有時，又將傾角σ＜ 45°的逆斷層特別稱為沖斷層（thrust fault），將δ＜ 10°的逆斷層特別稱為上沖斷層或逆沖斷層（overthrust fault）。作為舉例，圖17 以震源球下半球等面積投影表示走向為N-S 方向（?=0°），傾角為45°（δ=45°）的斷層面當滑動角λ由0°增至330°時震源機制解所表示的斷層滑動類型的變化。圖中，黑色區域表示初動為壓縮（+）的區域，白色區域表示初動為膨脹（－）的區域。以這種投影圖的方式表示的震源機制解（斷層面解）在西方形象地稱為“海灘球（beach ball）”或“沙灘球”，在我國則形象地稱為“西瓜皮”。圖18 則以投影圖即“海灘球”或“西瓜皮”（左圖）和側視圖（右圖）表示走向為N-S 方向（?=180°），傾角δ=45°的幾種震源機制解（Ben-Menahem and Singh，1981；Stein and Wysession，2003）。

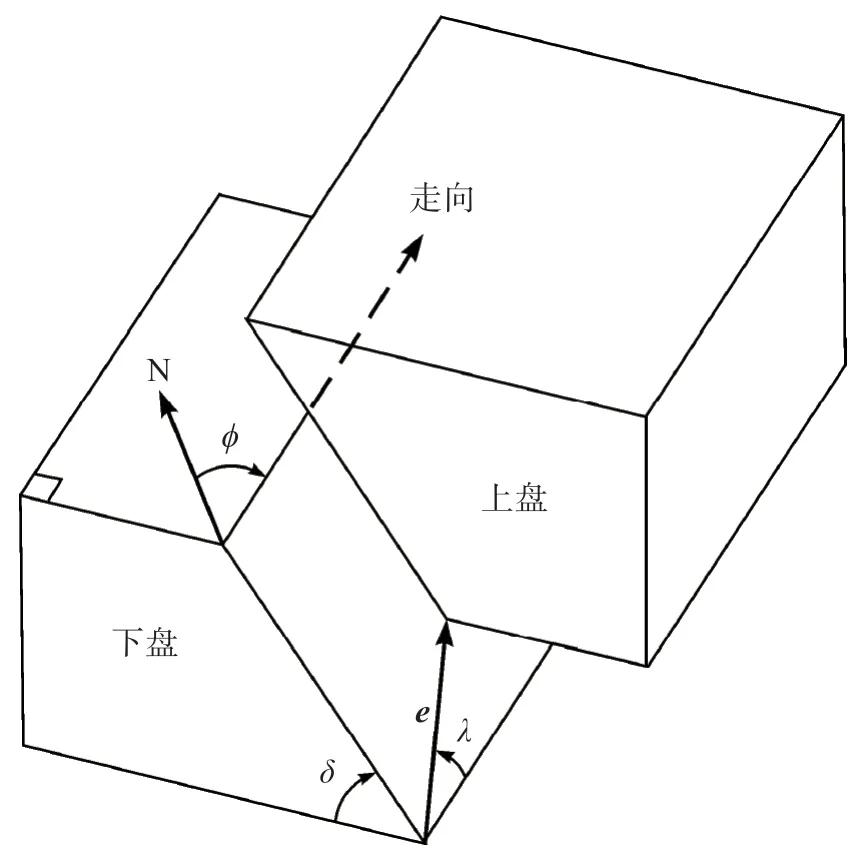
圖16 斜滑斷層圖中表示斷層面的走向?，傾向? +90°，傾角δ，斷層的上盤，下盤，滑動矢量e，滑動角λFig.16 Oblique fault The figure shows the strike ?,dip direction ?+90°,dip angle δ,the hanging and foot wall blcoks,slip vector e and slip angle λ of fault plane

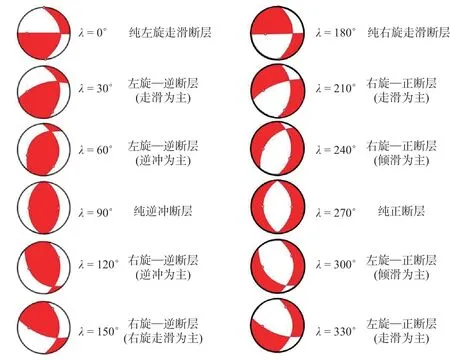
圖17 與各種不同的滑動角相應的地震的震源機制解當λ=0°，…，90°，…，180°，…，270°，…，330°時，由N-S 節面（?=0°，σ=45°的節面）所表示的震源機制，由純左旋走滑斷層（λ=0°），變至純逆沖斷層（λ=90°），變至純右旋走滑斷層（λ=180°），變至純正斷層（λ=270°），變至以走滑為主的左旋—正斷層（λ=330°）Fig.17 Focal mechanism for earthquakes with the same N-S striking fault plane（nodal plane ?=0°，δ=45°），but with slip angles varying from pure left lateral strikeslip（λ=0°）,to pure reverse dip-slip（λ =90°）,to pure right lateral strike-slip（λ=180°）,to pure normal dip-slip（λ=270°）,to mostly left lateral strike-slip with some normal dip-slip（λ=330°）

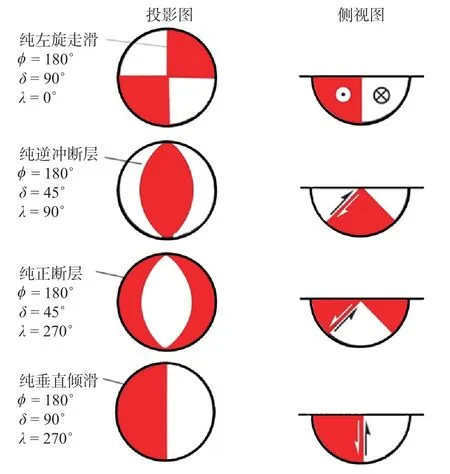
圖18 幾種地震震源機制解投影圖（左圖）與側視圖（右圖）Fig.18 Projection of solutions of several seismic source mechanisms（left）and side view（right）

表1 剪切滑動斷層的地質學術語Table 1 Geological terminology of shear slip fault

參考文獻（教程二）

Aki K and Richards P G.Quantitative Seismology:Theory and Methods,1 &2[M].San Francisco:W.H.Freeman,1980:1-932.安蕓敬一，P.G.理查茲.定量地震學.第1，2 卷[M].李欽祖，鄒其嘉，等譯.北京：地震出版社，1986：1-620，1-406.

Anderson E M.Dynamics of faulting[J].Trans Geol Soc Edinburgh,1905,8:387-402.

Anderson E M.The Dynamics of Faulting and Dyke Formation with Application to Britain[M].2nd edition.Edinburgh:Oliver and Boyd,1951:1-206.

Anderson E M.The Dynamics of Faulting[M].London:Oliver and Boyd,1942:1-183.

Atkinson B K.Fracture Mechanics of Rock[M].London:Academic Press,1987:1-534.Ben-Menahem A and Singh S J.Seismic Waves and Sources[M].New York:Springer-Verlag,1981:1-1 108.

Bullen K E.An Introduction to the Theory of Seismology[M].2nd edition.Cambridge:Cambridge University Press,1953:1-296.K E 布倫著.地震學引論[M].朱傳鎮，李欽祖譯，傅承義校.北京：科學出版社，1965：1-336.

Byerlee J D.Brittle-ductile transition in rocks[J].J Geophys Res,1968,73:4 741-4 750.

Byerlee J D.Friction of rocks[C]//Proc.Conf.II Experimental Studies of Rock Friction with Application to Earthquake Prediction,USGS,1977:55-77.

Byerlee J D.Friction of rocks[J].Pure Appl Geophys,1978,116:615-626.

Byerlee J D.Frictional characteristics of granite under high confining pressure[J].J Geophys Res,1967,72:3 639-3 648.

Coulomb C A.Theorie des Machines Simples//Memoires de Mathématique et de Physique de l’Académie Royale des Sciences,1785:161.

Jaeger J C and Cook N G W.Fundamentals of Rock Mechanics[M].3rd edition.London:Chapman and Hall,1979:1-593.

Jaeger J C.Elasticity,Fracture and Flow,with Engineering and Geological Applications[M].2nd edition.London:Methuen,1962:1-212.

Jeffreys H.On the mechanics of faulting[J].Geol Mag,1942,79:291-295.

Jeffreys H.The Earth:Its Origin,History,and Physical Constitution[M].6th edition.Cambridge:Cambridge University Press,1976:1-574.H.杰弗里斯.地球：它的起源、歷史和物理組成[M].張煥志，李致森譯.北京：科學出版社，1985：1-437.

Lay T and Wallace T C.Modern Global Seismology[M].New York:Academic Press,1995:1-521.

Stein S and Wysession M.An Introduction to Seismology,Earthquakes,and Earth Structure[M].Malden,MA:Blackwell Publishing,2003:1-498.

Turcotte D L and Schubert G.Geodynamics[M].4th edition.Cambridge:Cambridge University Press,2001:1-456.