準確度優先的多目標帝王蝶優化定量構效特征選擇方法

李小林，王 靜，張元孜，黃世國

(福建農林大學 計算機與信息學院，福州 350002) E-mail：fjhsg25@126.com

1 引 言

帝王蝶算法(Monarch Butterfly Optimization，MBO)是一種新的群體智能優化算法，通過模擬帝王蝶遷徙的行為實現尋優過程[1].為了避免算法過早收斂，通過結合和聲搜索操作[2]或結合自適應交叉算子和貪婪策略[3]對該算法進行了改進.馮艷紅等[4]在帝王蝶算法上結合差分變異策略來生成新個體，提高了獲得折扣{0，1}KP問題全局最優解的概率.針對TSP問題，Wang等[5]提出了一種二進制帝王蝶優化算法.

定量構效關系(Quantitative Structure-Activity Relationship，QSAR)的目標是建立化合物的結構性質和相應的生物活性之間的關系[6].化合物的結構由各種特征(分子描述符)進行編碼來描述.然而，并不是所有的特征都與其生物活性相關.特征太多可能導致模型過擬合，特征太少則可能會導致欠擬合[7].只包含相關和無冗余特征的最優特征子集能夠提高QSAR模型預測的精度和可解釋性[8].因此，特征選擇成為QSAR研究的關鍵預處理步驟.

元啟發式算法因其較強的全局搜索能力和潛力已成功應用于QSAR特征選擇.這些代表性的方法包括遺傳算法[9，10]，粒子群優化[11，12]，差分進化算法等.

針對QSAR特征選擇需在優先滿足最大化準確度前提下同時最小化特征數的多目標要求，本研究在MBO算法的粒子排序步驟中采用了非支配排序算法，并修改了調整算子；采用準確度優先的策略，改善了傳統多目標算法在低準確度區域耗費大量計算資源的缺陷；采用分小組使用不同突變策略的方法解決了算法早熟的問題.實驗結果表明，這些策略的綜合應用提升了MBO算法的性能，實現了QSAR建模提高準確度并減少特征數的目的.

2 定量構效建模

為了建立化合物結構特征與其活性之間的關系，采用機器學習方法來建立二者的關聯.其中偏最小二乘法(Partial Least Squares，PLS)常用于預測化合物結構特征與其相應的生物活性或化學性質之間的關系.偏最小二乘法通過具有因子分析的線性多元模型將兩個數據矩陣x和y聯系起來[13].在QSAR建模中，x表示所有化合物的特征向量，y表示相應化合物的活性.

用Q2值衡量QSAR建模的精度，定義如式(1)所示：

(1)

3 帝王蝶優化算法

帝王蝶優化算法模擬了帝王蝶的遷移行為[1].其行為簡單描述為：1)帝王蝶的整個種群被分為兩個子種群，稱為子種群1和子種群2；2)每個子種群中更優的子代個體將分別由遷移操作算子或調整算子產生，并取代其父代個體；3)當前最優的個體自動存活到下一代.

假設問題對應于一個d維解空間，初始化產生一個大小為NP的種群P=(X1，X2，…，XN)，第i個個體在解空間的位置可以表示為一個d維向量Xi=(xi，1，xi，2，…，xi，d)T，顯然，每個個體的位置都對應著目標問題的一個潛在解.其遷移算子和調整算子描述如下.

設NP1和NP2分別為兩個子種群中個體數量，p為子種群1個體的占比，即NP1=ceil(p×NP)，NP2=NP-NP1.其中，函數ceil(c)表示向上取整.遷移算子的數學模型描述如式(2)所示：

(2)

其中，i=1，2，…，N1，t表示當前迭代次數，xr1和xr2分別表示帝王蝶個體r1和r2的位置，這兩只帝王蝶分別隨機取自兩個子種群.標量r=rand×peri，rand是[0，1]間的一個隨機數；peri代表遷移周期.

在調整算子中，若rand≤p，則子種群2中個體按式(3)更新：

(3)

其中，i=1，2，…，N2.xbest表示全局最優個體的位置.

否則，個體將按式(4)更新：

(4)

其中，xr3表示從子種群2中隨機選擇的一個帝王蝶的位置.

(5)

(6)

其中，α是權重因子，由α=Smax/t2計算所得，Smax表示帝王蝶的最大步長.dx表示帝王蝶的步長，由Levy函數計算.BAR表示調整率.以最小值優化為例，MBO算法的步驟如算法1所示.

算法1.MBO算法偽代碼

初始化參數：種群大小NP，子種群1中個體的比例p，調整率BAR，遷移周期peri，權重因子α，最大步長Smax，t=1，最大評價次數T；

隨機初始化大小為NP的種群；

計算種群中每個個體的適應度值；

Whilet≤Tdo

根據適應度值對所有個體進行排序；

適應度值較小的前p×NP個個體組成子種群1，其余個體組成子種群2；

For子種群1中的每個個體

根據公式(2)進行個體的更新；

End

For子種群2中的每個個體

根據公式(3-6)進行個體的更新；

End

將兩個更新后的子種群合并成一個種群；

計算種群中每個個體的適應度值；

t=t+1；

End

輸出最優個體的位置xbest及其對應的適應度值f(xbest).

4 準確度優先的多目標帝王蝶優化QSAR特征選擇

4.1 二進制帝王蝶特征選擇算法

傳統的帝王蝶優化算法的目標是在連續數據空間中尋找最優解.但特征選擇是在二進制空間中搜索最優解.為了解決QSAR特征選擇的問題，每個個體均表示為一個二進制字符串.字符串的長度等于特征的數量.字符串中的“1”表示選擇了對應的特征，“0”表示未選擇對應的特征.同時，偏最小二乘法用于計算每個個體的適應度值.

二進制帝王蝶優化(Binary Monarch Butterfly Optimization，BMBO)算法的過程與標準帝王蝶優化算法相似，只在兩個地方做了修改：

1)在初始化階段，所有個體的位置均隨機生成，然后根據給定閾值轉換成二進制字符串.

2)因在調整算子中獲得的值是連續值，使用Tanh()傳遞函數[14]將其映射為二進制值.故當rand>BAR時，公式(5)修改為：

(7)

需要注意的是，為了適應最小值優化，本研究用準確度的負值即-Q2作為適應度函數.

4.2 快速非支配排序策略

為了同時滿足最小化準確度負值和最小化特征數的要求，引入了非支配排序算法.

首先，快速非支配排序涉及到的概念有如下兩點：

1)對于兩個向量x和y，當且僅當：

(8)

我們稱x支配y，表示為xy，否則，這兩個向量互不支配.

2)對于一個解x∈X，當且僅當：

{?x∈X|xjxi，i≠j}

(9)

則稱該解x為帕累托最優.所有帕累托最優解的集合稱為帕累托解集，定義如式(10)所示：

Ps={xi，xj∈X|?xjxi，i≠j}

(10)

一個包含帕累托解集目標函數值的集合稱為帕累托前沿，表示為式(11)：

Pf={f(xi)|xi∈Ps}

(11)

因此，快速非支配排序算法對每個解x均需計算兩個參數：1)種群中支配x的個體的數目nx；2)種群中被x支配的個體的集合Sx.

快速非支配排序的整個過程描述如下：

1)找到nx=0的個體，然后將這些個體存儲到當前集合Fi中，其中i代表級別；

2)找出在Fi中由x支配的個體的集合Sx.對于Sx中的每個個體x，用nx-1更新nx.如果nx=0，則將x存儲在集合H中.

3)F1中的個體為第一非支配水平的個體.H代表當前集合.重復上述這些步驟，直到所有的個體被分配到不同級別的集合為止.

同時，還對調整算子進行了修改.與傳統的非支配排序算法不同，我們只考慮第一層帕累托前沿F1，并且只計算F1中個體的擁擠度.當rand≤p時，調整算子中的個體按照式(12)進行更新：

(12)

4.3 準確度優先策略

該策略的思想是當子代個體擁有更好的精度時，對應的父代個體將會被其取代.增加該策略的原因是：在QSAR建模中，模型的準確度指標優先于特征數指標.采用準確度優先策略可以避免多目標算法耗費大量計算資源來搜索低準確度的空間，即圖1中矩形框內的區域.

圖1 低準確度的區域示意圖Fig.1 Illustration of region with the low accuracy

4.4 突變策略

為了解決早熟的問題，整個種群分為子組1、子組2和子組3，每個子組的個體數量均為NP/3.子組1中的突變率設置為隨著迭代次數的增加而降低，子組2的突變率則設置為隨機數，子組3中的個體不進行突變.

4.5 準確度優先的多目標帝王蝶優化QSAR特征選擇的基本框架

綜合上述3個策略，準確度優先的多目標帝王蝶優化(Accuracy Prior Multi-Objective Monarch Butterfly Optimization，APMOMBO)QSAR特征選擇的步驟如算法2所示.該算法最終輸出的最優粒子是準確度最高的粒子.

算法2.準確度優先的多目標帝王蝶優化QSAR特征選擇算法偽代碼

初始化參數：種群大小NP，子種群1的個體占比p，調整率BAR，遷移周期peri，最大步長Smax，t=1，最大評價次數T；

隨機初始化大小為NP的種群；

通過偏最小二乘法計算種群中每個個體的適應度值，并統計每個個體所選擇的特征數量；

通過非支配排序策略對種群中所有個體進行排序；

Whilet≤Tdo

根據p將種群分成子種群1和子種群2；

For子種群1中的每個個體

根據公式(2)進行個體的更新；

End

For子種群2中的每個個體

根據公式(7)和公式(12)進行個體的更新；

End

將兩個更新后的子種群合并成一個種群，并將該種群分成子組1、子組2和子組3；

根據突變策略對前兩個子組中的個體進行變異操作；

通過偏最小二乘法計算種群中每個個體的適應度值，并統計每個個體所選擇的特征數量；

根據準確度優先策略更新子組1和子組2中的父代個體；

將所有子組合并為一個種群；

通過非支配排序策略對種群中所有個體進行排序；

t=t+1；

End

輸出最優個體的位置xbest及其對應的適應度值f(xbest).

5 算法性能測試

5.1 實驗設置及性能指標

為了測試我們提出的算法的特征選擇性能，本文選擇了文獻[11]中的3個基準數據集，如表1所示.

表1 測試數據集Table 1 List of datasets used in the experiments

同時，將提出的APMOMBO算法和BMBO、PSO和WS-PSO進行比較.在本文中BMBO和APMOMBO算法的相關參數設置為：NP=150，p=0.5，BAR=0.5，peri=1.2，Smax=1.0，T=20000.除種群數量和評價次數分別為150和20000外，PSO和WS-PSO算法的其它參數設置與文獻[11]相同，即PSO的學習率a=0.5，WS-PSO的學習率a=0.5，b=0.8，突變率c=0.05以及加權抽樣比例為α=0.5.偏最小二乘法中潛在化合物的最大數量被設置為20，并且通過5折交叉驗證來確定潛在化合物的最佳數量.為了消除隨機性，所有算法在3個數據集上均獨立運行100次.本文所有實驗在硬件配置為Intel(R)Core(TM)i5-7500 CPU @3.40GHz、內存為16.0GB的計算機上進行，操作系統為Microsoft Windows 10.編程語言為MATLAB，編譯環境為MATLAB R2018b.我們使用文獻[11]中描述的5折交叉驗證方法來評估QSAR特征選擇的性能.本文的性能指標包括準確度Q2、均方根誤差[15](表示為RMSECV)和特征數量(表示為NSD).準確度的值越大越好，其它兩個指標則越小越好.同時，我們還計算了各指標的標準差.

5.2 性能比較與分析

由于BMBO未在QSAR建模特征選擇中得到應用，我們給出了BMBO和PSO和WS-PSO的比較結果，如表2所示，其中粗體為較優結果.在準確度Q2和均方根誤差RMSECV方面，BMBO的性能均優于PSO及WS-PSO算法，且標準差相對更低.這表明將BMBO算法用于QSAR建模特征選擇，可以保持較高的準確度和穩定性.但BMBO算法在Artemisinin數據集和Selwood數據集的降維效果較差，這說明需要進一步改進BMBO的降維性能.

為了評估不同策略與BMBO算法結合的性能和效率，我們將3個策略逐個添加到BMBO算法中，得到3個不同的算法，即僅采用快速非支配排序策略的二進制帝王蝶優化算法(稱為IBMBO-1)，同時采用快速非支配排序策略和準確度優先策略的二進制帝王蝶優化算法(稱為IBMBO2)，以及同時采用快速非支配排序策略、準確度優先策略以及突變策略的二進制帝王蝶優化算法即APMOMBO.表3給出了BMBO和上述不同策略結合的實驗結果，其中粗體為較優結果.

從表3可以看出，IBMBO-2和APMOMBO在準確度和均方根誤差方面比IBMBO-1表現更好，而在特征數量方面比IBMBO-1表現得差.這表明，準確度優先策略和準確度優先+突變策略有利于提高特征選擇的準確性和穩定性，僅使用快速非支配排序算法很難搜索到所有有用的特征來保持較高的準確性.與IBMBO-2相比，APMOMBO除了在Selwood數據集的特征數量之外的所有性能指標上都有提升.結果表明，采用突變策略避免了早熟，提高了精度，減少了均方根誤差和特征數.

對比表2和表3中的數據可以看出，APMOMBO在3個性能指標上都比BMBO、WS-PSO和PSO表現得更好.這說明改進的BMBO算法通過使用快速非支配排序、準確度優先和突變策略，提高了精度，減少了均方根誤差和特征數量.

表2 3種算法用于QASR建模特征選擇的性能指標對比Table 2 Comparison of the algorithms for feature selection in QSAR

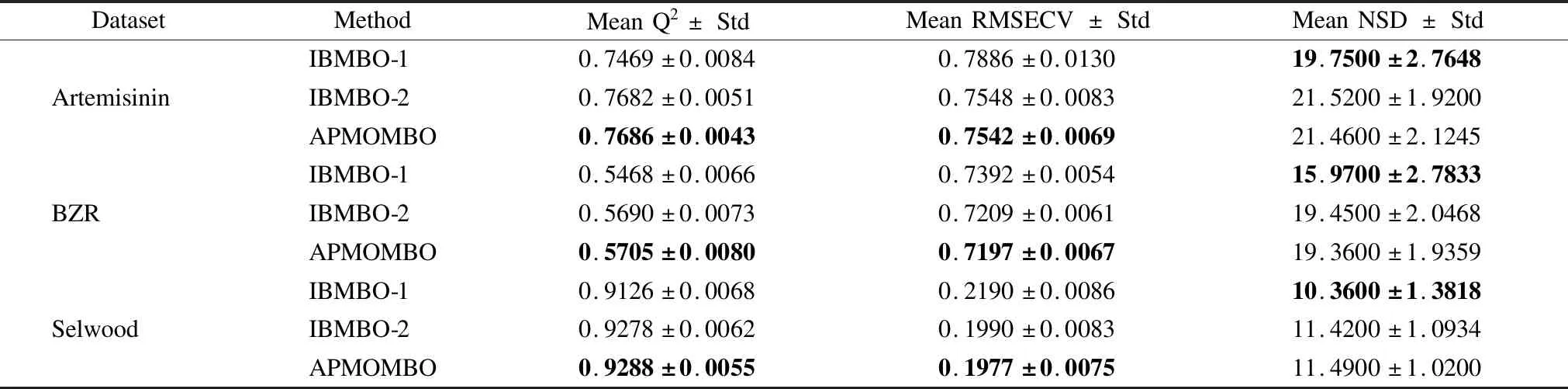
表3 BMBO算法結合3種策略的實驗結果Table 3 Experimental results of BMBO algorithms with three strategies

6 總 結

在本文中，我們應用二進制帝王蝶優化來選擇分子描述符用于QSAR建模，并且結合快速非支配排序、準確度優先和突變3種策略來提高BMBO的性能.

對BMBO和準確度優先的多目標帝王蝶優化QSAR特征選擇方法在3個基準數據集上進行了測試.實驗結果表明BMBO算法可以用于QSAR特征選擇，其在準確度和均方根誤差上的性能均優于PSO和WS-PSO，但在降維方面略有不足.而準確度優先的多目標帝王蝶優化QSAR特征選擇方法則在所有指標上均優于PSO、WS-PSO和BMBO算法.這表明快速非支配排序、準確度優先和突變策略提高了特征選擇的準確度，降低了均方根誤差，并減少了特征的數量.該算法可有效實現QSAR建模中的特征選擇.