基于ARIMAX-BP神經網絡組合模型的新疆小麥產量-播種面積-種植結構預測研究

徐剛剛,阿麗米熱·蘇萊曼，謝佳洋

(新疆農業大學 數理學院，新疆 烏魯木齊 830052)

0 引言

小麥是新疆主要的糧食作物，為全疆糧食的供需提供安全保障.近年來隨著小麥、玉米等糧食作物的供給側結構性改革，多項惠農政策的扶持以及農業部門的專業人員在育種、灌溉、施肥等方面的技術指導，小麥產量、播種面積以及種植結構等方面都有了較大的變化，達到了農民增收、農業增效的目的.

目前對有關小麥產量、播種面積以及種植結構等方面的預測也有很多文獻.李曄等[1]利用新維無偏灰色馬爾可夫模型預測小麥的產量，得出該模型適合中長期預測的結論；林瀅等[2]通過隨機森林算法預測河南冬小麥產量的最佳時間窗和影響因子，結果表明，隨機森林算法適用于河南省冬小麥產量預測，并且適用于短期預測；張明輝[3]利用層次分析法預測小麥產量，結果表明：組合模型能夠較好地監測與預測小麥產量；舒服華[4]利用NAR神經網絡算法對河南小麥產量進行預測，結果表明，NAR神經網絡算法適合于河南小麥產量的預測，并且誤差較小；王寧等[5]對2000～2019年河南省小麥播種面積與產量變化趨勢分析，結果表明，河南省的小麥播種面積和小麥產量將繼續增加.以上文獻都是基于一種模型進行研究.對于新疆小麥的研究，主要集中在栽培技術、病蟲害等方面.而對新疆各地州小麥產量、播種面積等方面的預測較少.因此，本文通過建立ARIMAX-BP神經網絡組合模型來擬合新疆小麥的產量、播種面積以及全國小麥的種植結構，進一步預測新疆小麥在這些方面的發展趨勢，為決策者提供可靠的理論依據.

基于此，為了更全面預測新疆小麥產量、播種面積及全國小麥種植結構，本文從《中國統計年鑒》選取1999～2020年新疆小麥產量、播種面積以及全國小麥種植結構數據為預測對象，以耕地灌溉面積、農用化肥施用量及農業機械總動力三組時間序列數據為解釋變量，建立多元時間序列ARIMAX模型、BP神經網絡算法以及它們的組合模型進行分析.經檢驗及比較，組合模型提高了預測的精度，避免了單一模型提取數據信息的不足，同時用多維數據建模更能反映新疆小麥的客觀現狀，更具有說服力.

1 理論模型與方法

1.1 ARIMAX動態回歸模型

其基本思想為[6]：假設輸出變量序列{Yt}和輸入變量序列{X1t},{X2t},…,{Xkt}均平穩，且兩組序列之間存在線性相關關系，為了討論輸入變量序列對輸出變量序列的影響，這里引入第i個輸入變量序列{Xit}對輸出變量序列{Yt}影響的延遲期數為li，有效作用期數為ni.Box和Jenkins通過引入輸出變量序列的自回歸結構，使模型的階數減少，模型的具體表達式為

(1)

Φi(B)=1-φi1B-φi2B2- …-φipiBpi,1≤i≤k.

Θi(B)是第i個自變量{Xit}的qi階移動平均系數多項式

Θi(B)=θi0-θi1B-θi2B2- …-θiqiBqi,1≤i≤k.

且qi+pi遠小于ni.

由于序列{Yt},{X1t},{X2t},…,{Xkt}均是平穩序列，因此由式(1)可得殘差序列{εt}平穩.進一步利用ARMA模型提取殘差序列{εt}中的相關信息，

其中：Θ(B)為殘差序列的移動平均系數多項式；Φ(B)為殘差序列自回歸系數多項式；et是均值為零的白噪聲序列.最終得到輸出變量序列{Yt}和輸入變量序列{X1t},{X2t},…,{Xkt}的回歸模型稱為動態回歸模型，記為ARIMAX，具體形式為

1.2 BP神經網絡算法

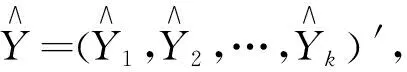
1.2.1 信號向前傳遞

當輸入訓練樣本為

Xs=(xs1,xs2,…,xsM)′,1≤s≤k，

M為樣本Xs的維數，則根據向前傳播方式，可得以下表達式：

(1)隱含層中有n1個神經元，第i個神經元的輸出為

(2)輸出層中有n2個神經元，第j個神經元的輸出為

j=1,2,…,n2.

(3)誤差平方和函數為

1.2.2 權值的調整及誤差的反向傳播

在BP神經網絡算法中，權值的調整量與輸出相對于期望響應的誤差對權值的偏微分大小成正比，符號相反.首先通過偏微分方法計算輸出層的權值調整量，具體計算過程為

定義局部梯度為

則輸出層的權值變化，從第i個輸入到第j個輸出的權值調整量為

同理可得偏差權值調整量為

通過以上推導，進一步迭代算出下一次權值ω2ji.

與輸出層權值調整量類似，隱層中從第m個輸入到第i個輸出的權值調整量為

同理可得偏差為

其中，n為迭代次數.

1.3 ARIMA-BP神經網絡組合模型

通常情況下，利用一種方法建模往往只能刻畫數據在某一方面的規律，容易忽略數據的綜合特征，導致預測精度不高.近年來隨著組合模型的出現，彌補了這方面的不足，使模型的預測精度得到了有效提高.組合模型是將多種單一模型通過加權進行組合，通過計算組合模型的誤差平方和并讓其達到最小時求出相應的組合權重，進而達到精準預測的效果.結合本文所研究數據的特征，將ARIMAX模型與BP神經網絡算法進行組合，利用組合之后的ARIMAX-BP神經網絡模型預測結果，預測流程如圖1所示.

用組合模型進行預測，最關鍵的技術是如何確定一套合理的組合權重.許多學者在這方面也做出了相應的研究，目前常用的權重確定方法有平均法、倒數法、熵權法等.例如Torbat等[8]用了一種混合概率ARIMA模型分析商品市場消費需求趨勢；羅文劼等[9]基于熵權-離差客觀組合賦權方法確定指標權重.

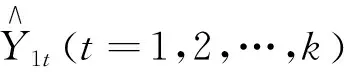
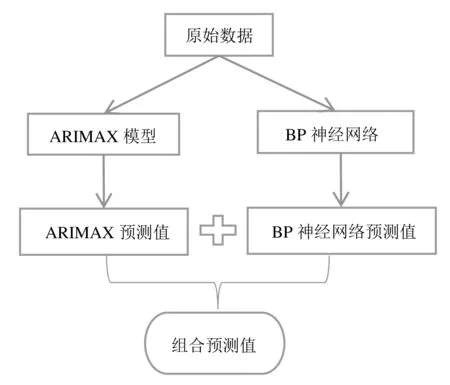
圖1 組合模型預測流程圖

設兩種預測方法的誤差矩陣e=(E1,E2)′,則組合預測的誤差信息陣為

記模型組合權重向量為

W=(ω1,ω2)′，ω1+ω2=0，ω1>0，ω2>0.

組合模型的預測值表示為

組合模型預測的誤差為

組合模型預測的誤差平方和為

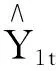
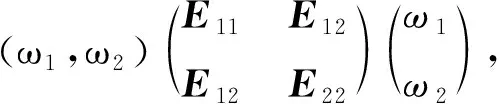
通過計算得到各自的權重及組合預測的誤差平方和為

2 新疆小麥發展趨勢預測

2.1 數據選取及處理

新疆小麥產量占據新疆糧食總產量的 41%以上，是新疆全區糧食安全發展的關鍵[11].為了研究新疆小麥發展現狀，從《中國統計年鑒》選取了1999～2020年新疆小麥產量(Y1t：萬噸)、新疆小麥播種面積(Y2t：千公頃)、全國小麥種植結構(Y3t：%)3個主要指標作為被解釋變量，以新疆耕地灌溉面積(X1t：千公頃)、新疆農用化肥施用量(X2t：萬噸)、新疆農業機械總動力(X3t：萬千瓦)3個方面的時間序列數據分別作為它們的解釋變量進行建模，分別表示為①、②、③.

在數據采集的過程中，2003年與2007年的個別數據缺失，為了便于分析，首先利用樣條插值法將原始數據中的缺失值進行插補，然后取對數，處理之后的數據記作{lnYit}與{lnXit},i=1,2,3;t=1999年,2000年,…,2020年.處理之后的時間序列圖如圖2所示.

從圖2能夠看出，小麥產量增長時段為1999～2000年、2004～2006年、2008～2011年、2012～2017年，產量下降年分為2000～2004年、2006～2008年、2011～2012年、2017～2020年；小麥種植面積與小麥產量具有同方向的增減趨勢；全國小麥種植結構在1999～2004年這段時間下降幅度較大，2004～2010年呈增長趨勢，2010～2020年大致呈緩慢下降趨勢；耕地灌溉面積、農用化肥施用量與新疆農業機械總動力總體為增長趨勢，并且各序列均表現出明顯的非平穩性，直接建模可能會產生偽回歸問題，即擬合得到的殘差序列非平穩.在實際研究中，若響應變量序列與解釋變量序列之間存在長期的均衡關系，即協整關系，說明殘差序列平穩，此時用非平穩序列也可以直接建模.

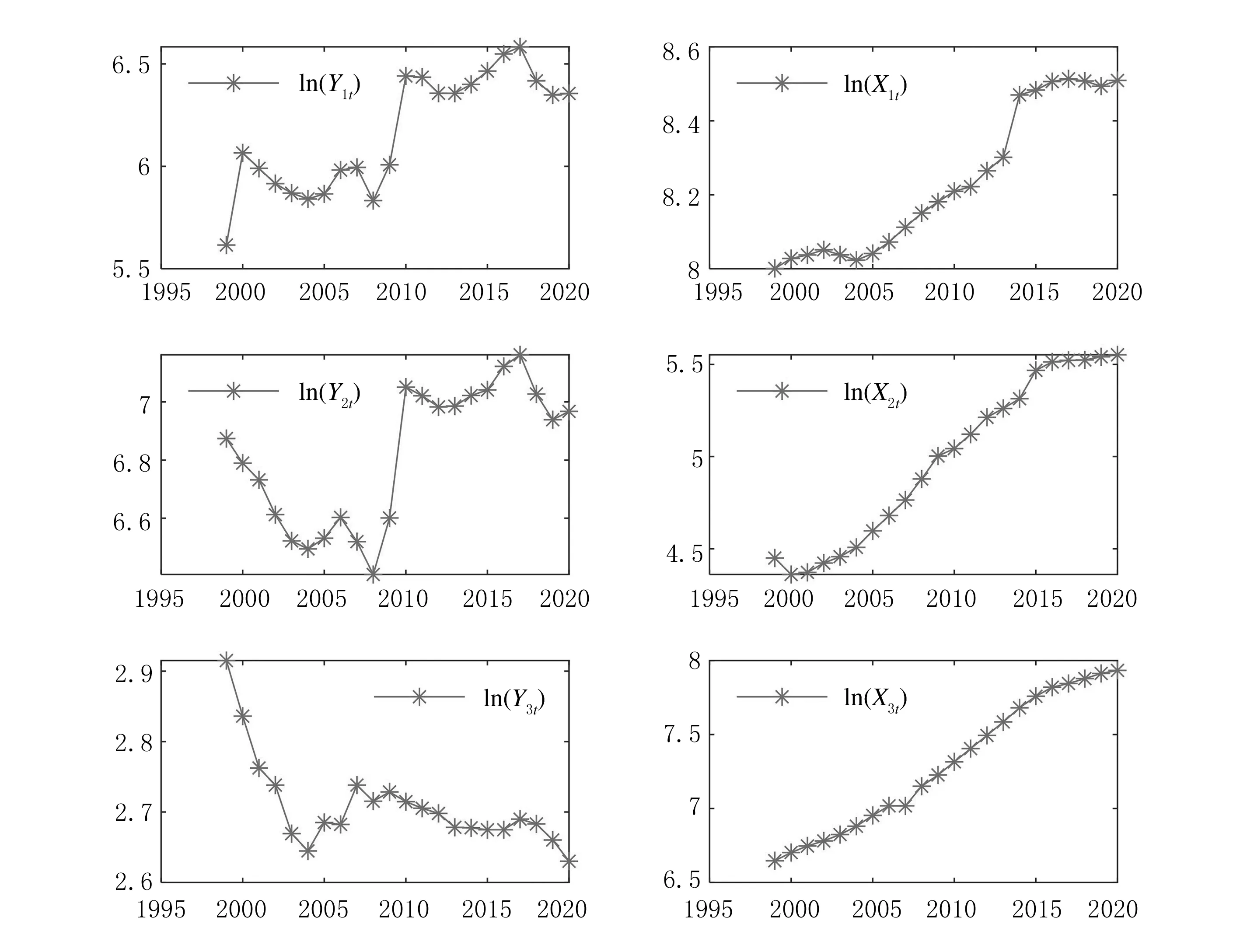
圖2 對原始數據取處理之后的時序圖

2.2 動態回歸模型ARIMAX預測

建立動態回歸ARIMAX模型之前，先對序列進行預白噪聲處理.即首先對單一序列{lnXit}建立合適的ARIMA模型，得到相應的殘差序列{εXit}.對序列{lnYit}實施同樣的變換，得到殘差序列{εYit}；然后考查{εXit}與{εYit}的互相關系數，判斷是否存在滯后效應，確定所要擬合的模型結構[12]；通過分析，初步建立響應序列{lnYit}與輸入序列{lnXit}間的ARIMAX模型，判斷得到的殘差序列{εit}是否平穩，若平穩，則模型可行，否則進一步用ARMA模型擬合殘差序列，直到最終的殘差序列為白噪聲序列.參數和模型均通過檢驗，此時認為得到的模型為最優模型，能充分提取數據的信息.殘差序列{εXit}與{εYit}的互相關系數如圖3所示.

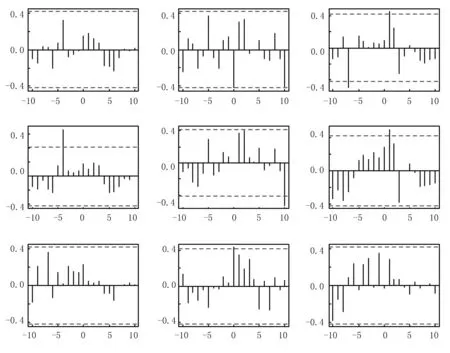
圖3 殘差序列{εXit}與{εYit}的互相關系數圖

圖3中最上面一行的三個圖為殘差序列{εY1t}與殘差序列{εXit}的互相關系數圖；中間一行為殘差序列{εY2t}與殘差序列{εXit}的互相關系數圖；第三行為殘差序列{εY3t}與殘差序列{εXit}的互相關系數圖.

從圖中可以看出，{εY1t}、{εY2t}都是滯后于{εX3t}1階時互相關系數最大，{εX2t}滯后于{εY2t}4階時互相關系數最大.結合以上分析及反復調試，最終模型的擬合結果與殘差序列的平穩性檢驗結果如表1所列.

表1 模型檢驗結果與殘差序列的白噪聲檢驗結果

表1是三組數據在ARIMAX模型擬合下的檢驗結果與相應的殘差序列的白噪聲檢驗結果，從檢驗結果可以看出：模型的擬合優度R2均大于0.8402，AIC值與誤差平方和(SSE1)都很小，即認為ARIMAX擬合結果較理想，提取了數據的大部分信息.此外，各模型的殘差序列檢驗的P值均大于顯著性水平0.05，不能拒絕原假設，即認為由ARIMAX模型擬合得到的各殘差序列均屬于白噪聲，且都達到平穩，因此所建模型合理.三個ARIMAX動態回歸模型的顯著性檢驗圖如圖4～圖6所示.

圖4 ARIMAX動態回歸模型①的顯著性檢驗圖

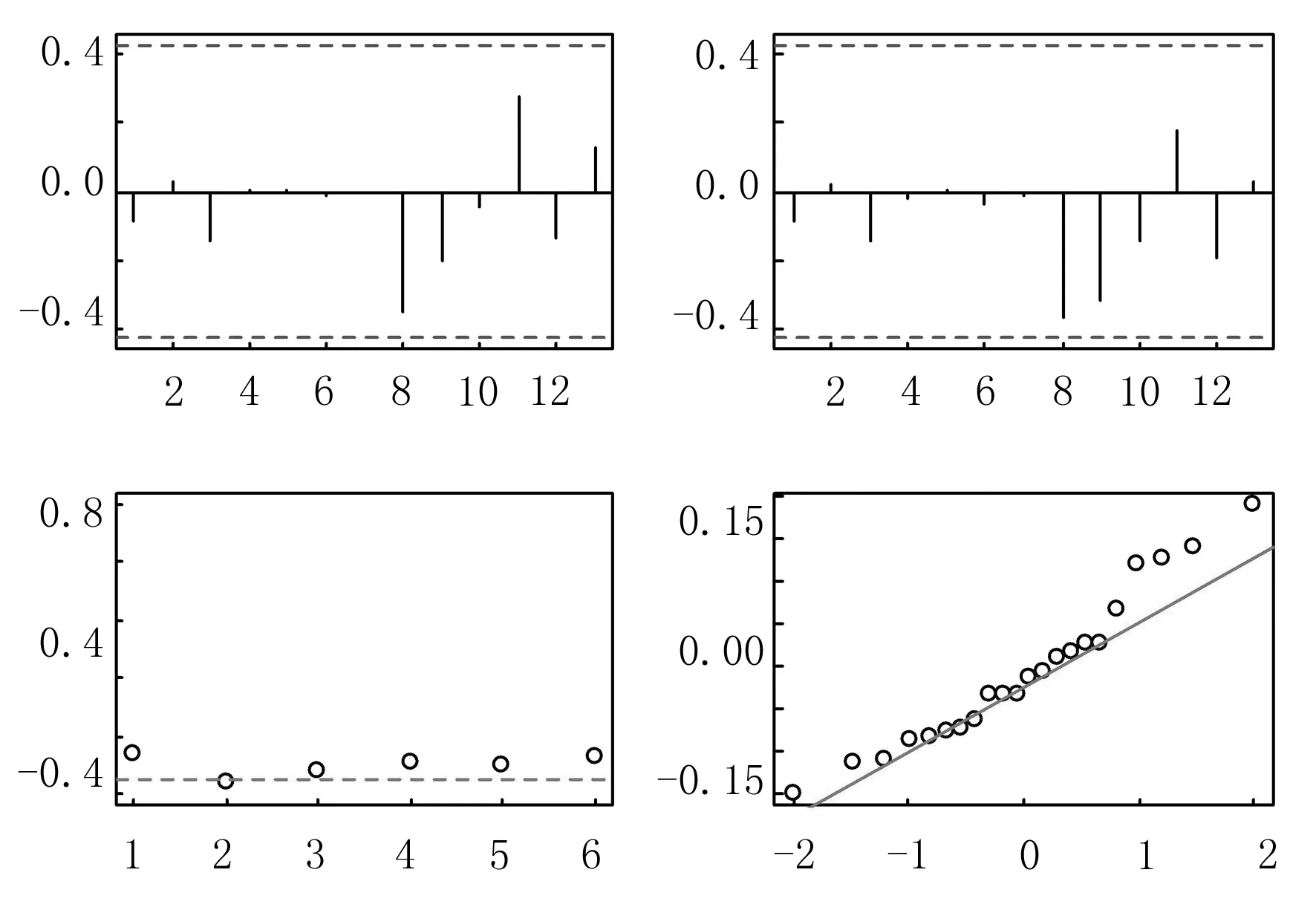
圖5 ARIMAX動態回歸模型②的顯著性檢驗圖

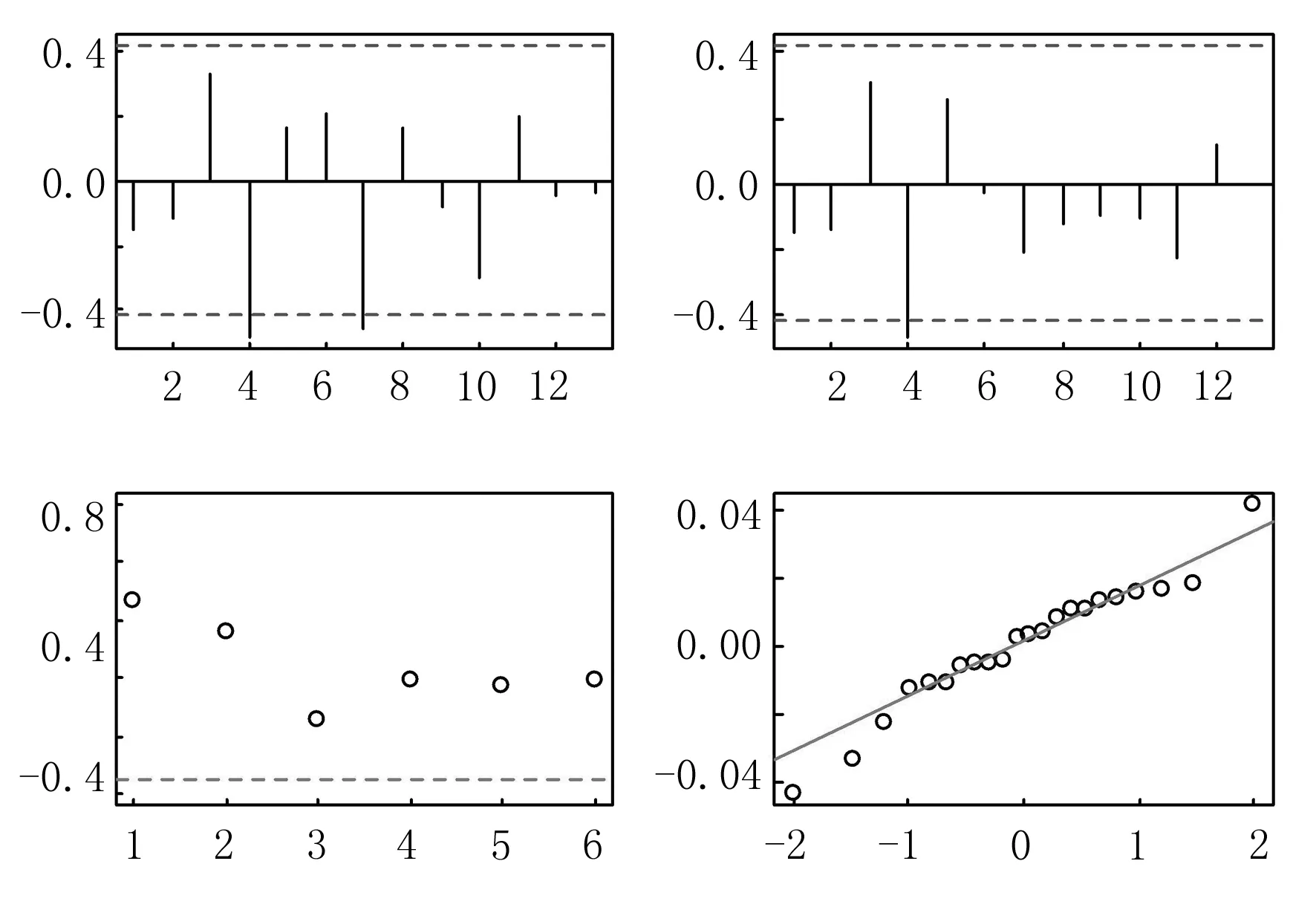
圖6 ARIMAX動態回歸模型③的顯著性檢驗圖

從圖4～6可看出：三個模型擬合得到的殘差序列均為白噪聲序列，與表4中的檢驗結果吻合，說明擬合的協整動態回歸模型顯著成立.

序列{lnYit}與自變量序列{lnXit}之間的長期均衡關系為

其中：at～N(0,0.011)；ε2t～N(0,0.008)；ε3t～N(0,0.0003).

2.3 BP神經網絡預測

神經網絡的輸入層為{lnXit}，輸出層為{lnYit}.在訓練過程中設定學習率為0.001，學習次數為10000，擬合誤差為10-4.得到合理的BP神經網絡模型后，再將原輸入層的序列數據回代預測，計算出相應的誤差平方和SSE2、擬合優度R2等檢驗指標值，結果如表2所列.

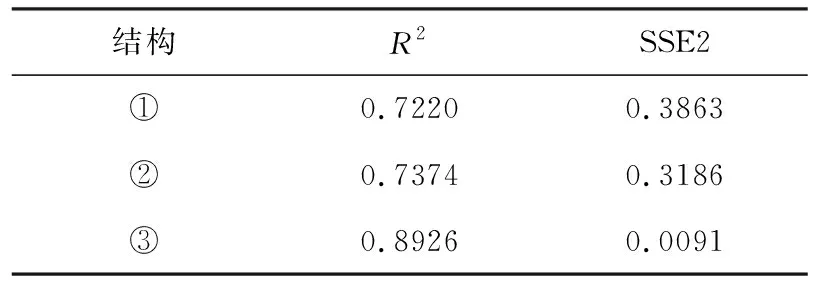
表2 BP神經網絡算法擬合的檢驗結果

表2為BP神經網絡算法的擬合優度R2與相應的誤差平方和SSE2，從兩個評價指標可以看出：擬合優度R2均大于0.72，誤差平方和SSE2均小于0.4，因此認為BP神經網絡模型擬合數據的結果較好，基本提取了數據的大部分信息.

2.4 ARIMAX-BP神經網絡組合模型預測

通過對ARIMAX模型與BP神經網絡模型擬合結果的比較得知兩種模型的擬合優度R2與誤差平方和SSE結果表現較好.總體來說，ARIMAX模型優于BP神經網絡模型，但是二者在預測結果方面存在一定的差異，因此考慮用二者的組合模型進一步預測.根據本文組合預測權值與總誤差平方和的計算方法，計算得到三組數據的ARIMAX模型與BP神經網絡算法的組合權重如表3所列.

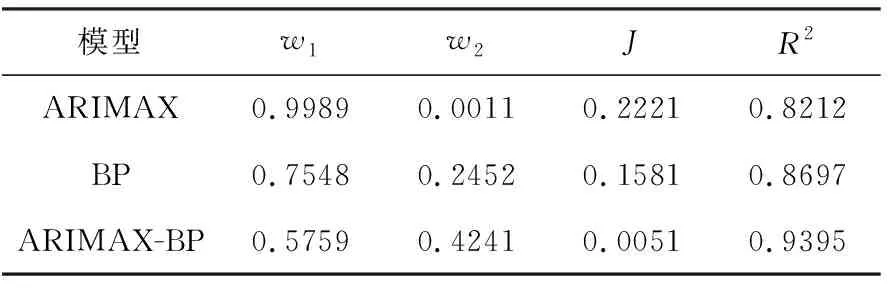
表3 組合模型的權重與總誤差平方和

從表3中可以看出：三組數據的ARIMAX模型的權重大于BP神經網絡算法的權重，說明數據更依賴于ARIMAX模型.從誤差平方和來看，組合模型ARIMAX模型>BP神經網絡算法.這充分體現了組合模型對新疆小麥產量、播種面積、全國小麥種植結構的預測效果較其他兩個單一模型更優，擬合精度更高.

三種模型的擬合情況如圖7～圖9所示.由于組合模型具有ARIMAX模型與BP神經網絡模型雙方面的特點，因此從圖中也可以看出：組合模型的預測值更接近真實值，更能刻畫數據波動的規律性.

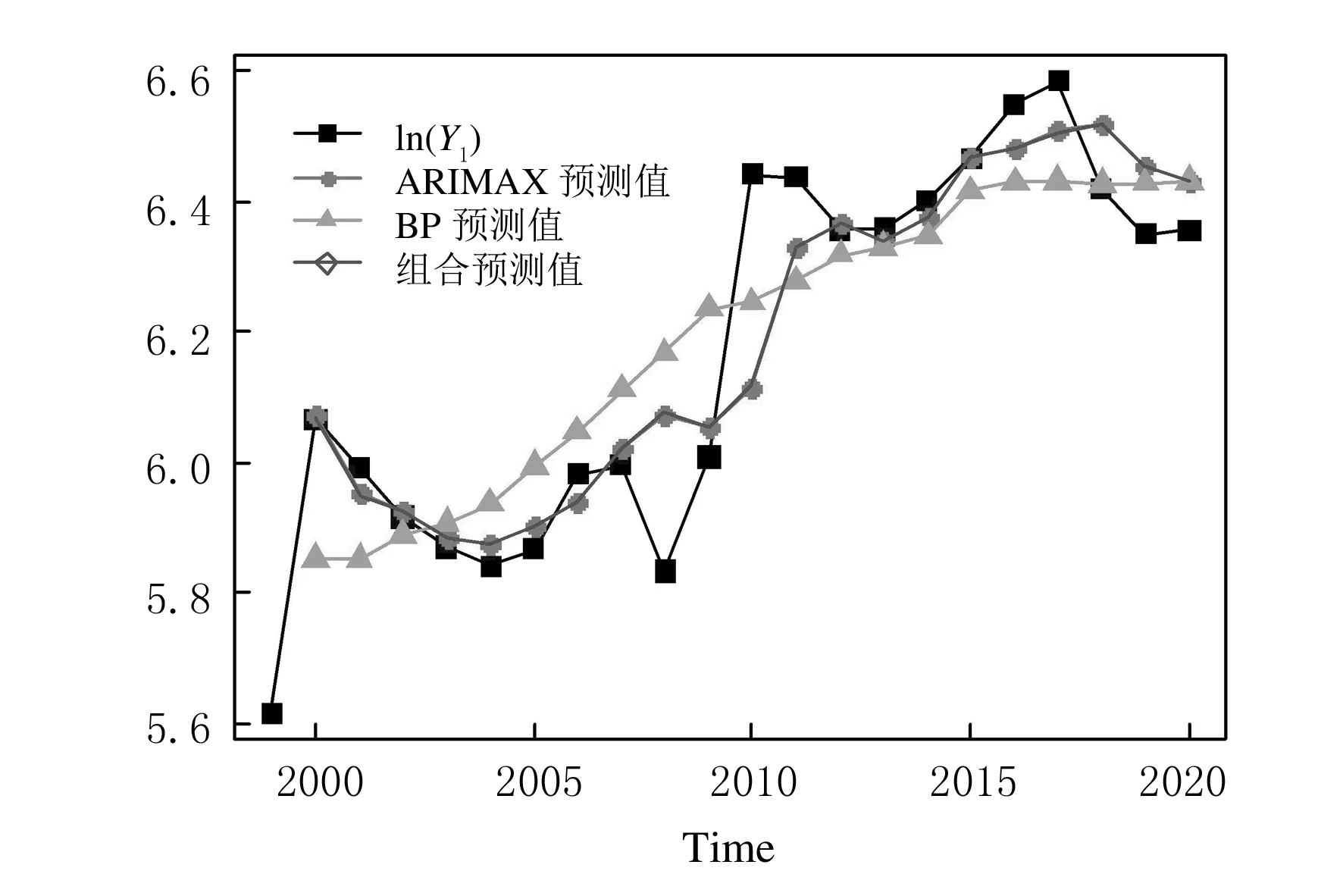
圖7 三種模型對lnY1t的預測結果圖

圖8 三種模型對lnY2t的預測結果圖

圖9 三種模型對lnY3t的預測結果圖

3 結論

本文建立多元時間序列回歸ARIMAX模型、BP神經網絡算法及二者的組合模型，通過回代法預測1999～2020年新疆小麥產量、新疆小麥播種面積以及全國小麥種植結構數據的波動規律，并根據每種方法預測的誤差平方和、擬合優度等指標評價模型的優劣，得到如下結論.

第一，經過模型檢驗與評價，兩種單一模型在預測本文數據時表現較好，在刻畫本文數據上，多元時間序列回歸ARIMAX模型較BP神經網絡算法更具說服力，但是由于單一模型本身的限制，仍然存在不能全面提取數據信息的可能性.通過組合預測權重法將兩種單一模型進行組合，組合模型汲取了單一模型的優點，預測精度得到了明顯提高，相應的擬合誤差也明顯比單一模型的誤差小.因此ARIMAX-BP神經網絡組合模型在預測新疆小麥產量、新疆小麥播種面積以及全國小麥種植結構上具有可行性.

第二，由組合模型的權重可知：ARIMAX模型的權重均大于BP神經網絡算法的權重，即組合模型更依賴于ARIMAX模型，因此可依照ARIMAX模型對新疆小麥產量、新疆小麥種植面積以及全國小麥種植結構波動的規律進一步解釋.首先對于新疆小麥產量來說，它主要受耕地灌溉面積與農用化肥施用量兩個變量的影響，并且均與小麥產量呈正相關關系，而農業機械總動力對新疆小麥產量的影響較小；其次對于新疆小麥播種面積來說，它受耕地灌溉面積的影響最大，農用化肥施用量與農業機械總動力影響相對較小；最后對于全國小麥種植化結構來說，它與農業機械總動力呈現很強的負相關關系，可以認為農業機械總動力在農業的其他方面應用較多，在小麥種植方面的投入較少，耕地灌溉面積與農用化肥施用量兩個變量與小麥種植結構呈正相關關系，這與小麥生產規律相符合.在本文研究過程中只用兩種模型進行組合，并未考慮更多模型；此外，對變量的選取方面還需進一步延伸，使預測結果更加準確，這也是后續有待完善的方面.