拉蓋爾-高斯光束雙縫衍射圖樣的仿真

徐全學 ,鄭思敏,王 濤

(1.拉薩師范高等專科學校 數學和自然科學系,西藏 拉薩 850007； 2.四川師范大學 物理與電子工程學院,四川 成都 610068)

1992年Allen等[1]在實驗中發現，光束在近軸傳播的近似條件下會形成具有螺旋相位波前或相位奇點的特殊光場,這種光束稱為渦旋光束,光束中的每個光子攜帶lh的軌道角動量, 該光束的表達式中帶有螺旋相位因子exp(ilθ)，其中l為拓撲荷數，θ為方位角.拉蓋爾-高斯光束是一種典型的人造渦旋光束,通常可以采用衍射光柵[2]、螺旋相位片[3]和全息叉形光柵[4]等方法生成.由于拉蓋爾-高斯光束在傳輸過程中能夠保持較高的穩定性，且具有軌道角動量和螺旋分布的相位結構，因此在光學俘獲、光鑷、量子信息處理、自由空間光通信等領域得到了廣泛應用[5-14].

近年來，渦旋光束的單縫衍射成為人們關注的熱點，國內外學者也對渦旋光束的衍射現象進行過相關研究.2008年，Soares等[15]通過拉蓋爾-高斯光束三角孔衍射實驗測量了拓撲荷值；2009年和2011年，王濤等[16]和高福海等[17]分別研究了拉蓋爾-高斯光束經過單縫衍射后的光強分布情況.2014年，諶娟等[18]對拉蓋爾-高斯光束中的圓孔衍射、單縫衍射和方孔衍射進行了研究，并分析了拉蓋爾-高斯光束的相位結構對光束衍射后場分布的影響.這些成果為推進渦旋光束衍射技術的應用奠定了重要的實驗與理論基礎，然而，到目前為止，還沒有關于渦旋光束經過雙縫衍射的報道，因此，本文將對此進行研究，并利用MATHCAD對條紋圖樣進行仿真，詳細討論了拉蓋爾-高斯光束的雙縫衍射圖樣光強分布特點及其影響因素.

1 理論分析

假設光源平面光束為拉蓋爾-高斯光束，其光場分布為[19]：

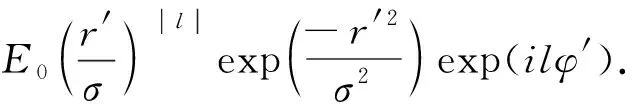
(1)

式中：E0為與光場振幅相關的常數，σ為光束的光斑大小，l為光束所帶拓撲電荷數，r′,φ′分別表示光源平面上任一點所對應的位置矢量的模和相位.

將(1)式寫成直角坐標形式為：

(2)

式中：arg表示復數的幅角.根據菲涅耳衍射積分，考慮到單縫衍射的方便，光束經過單縫后在衍射場中的光場分布可以寫成直角坐標的形式[16]：

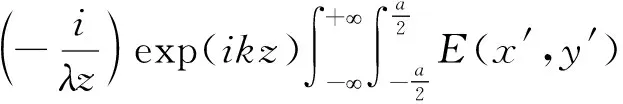
(3)

式中：(x′,y′)，(x,y)分別為光源平面和觀察平面的坐標，k為波數，z為衍射距離，a為單縫縫寬.從而可以得到衍射平面的光強和相位分布分別為[16]：

I(x,y,z)=E(x,y,z)E(x,y,z)*.

(4)

φ(x,y,z)=arg[E(x,y,z)].

(5)

根據菲涅耳衍射積分和拉蓋爾-高斯光束場強分布，基于以上理論推導，當拉蓋爾-高斯光束經過雙縫后的衍射光場可以表示為：

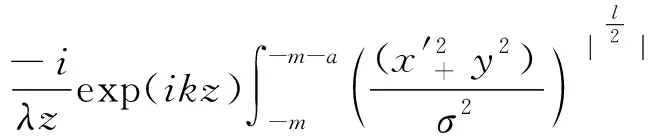
(6)

式中：(x′,y)，(x,y)分別為光源平面和觀察平面的坐標，k為波數，z為衍射距離，a為單縫縫寬，2m為雙縫間距(如圖1所示)，σ為光束的光斑大小,l為光束所帶拓撲電荷數.其中

(7)

為衍射平面的相位.

圖1 雙縫衍射示意圖

現在，我們考慮拉蓋爾-高斯光束經過雙縫衍射后的光強分布情況，其光譜強度可以通過下式來計算[16]：

I(x,y,z)=E(x,y,z)E(x,y,z)*.

(8)

2 數值模擬

將式(6)～(8)導入MATHCAD仿真平臺，模擬出了拉蓋爾-高斯光束照射雙縫后的衍射圖樣(圖2～圖6).從圖中可以清楚地看到：衍射圖樣是一組和狹縫平行且明暗交替分布的條紋，中央零級出現了兩條光強相等的亮條紋(主極大)，且其強度遠大于兩側亮紋(次極大)，而兩側亮紋隨著條紋級數的增加，光強逐漸減小.

圖2 a1=a2=0.3 mm，m=0.4 mm，z=1 m，σ=5 mm時，不同拓撲電荷數的衍射圖樣

圖2討論了不同拓撲荷值對衍射條紋光強分布的影響.從圖中我們發現，對于同一個x值，沿著y軸正方向看去，當拓撲荷值n=-1 時(如圖(a)所示)，衍射條紋從左向右發生了移動，且所有條紋中央光強減弱；當拓撲荷值n=1 時(如圖(c)所示)，衍射條紋從右向左發生了移動，同樣所有條紋中央光強減弱；而當拓撲荷值n=0 時(如圖(b)所示)，衍射條紋是明暗相間的直線條紋，且條紋中央光強明顯加強.可見拓撲荷值的大小和正負對衍射條紋的形狀和光強能夠產生一定的影響.

圖3 a1=a2=0.3 mm，m=0.4 mm，n=1，σ=5 mm時,不同衍射距離值的衍射圖樣

圖3討論了衍射距離對衍射條紋光強分布的影響.從圖3(a)～(c)可以觀察到，隨著衍射距離的增大，條紋間距也逐漸增大，條紋彎曲度越明顯，即衍射現象越顯著.由此可以判定，條紋間距跟衍射距離成正比，通過條紋間距的大小定性判斷衍射距離的遠近.

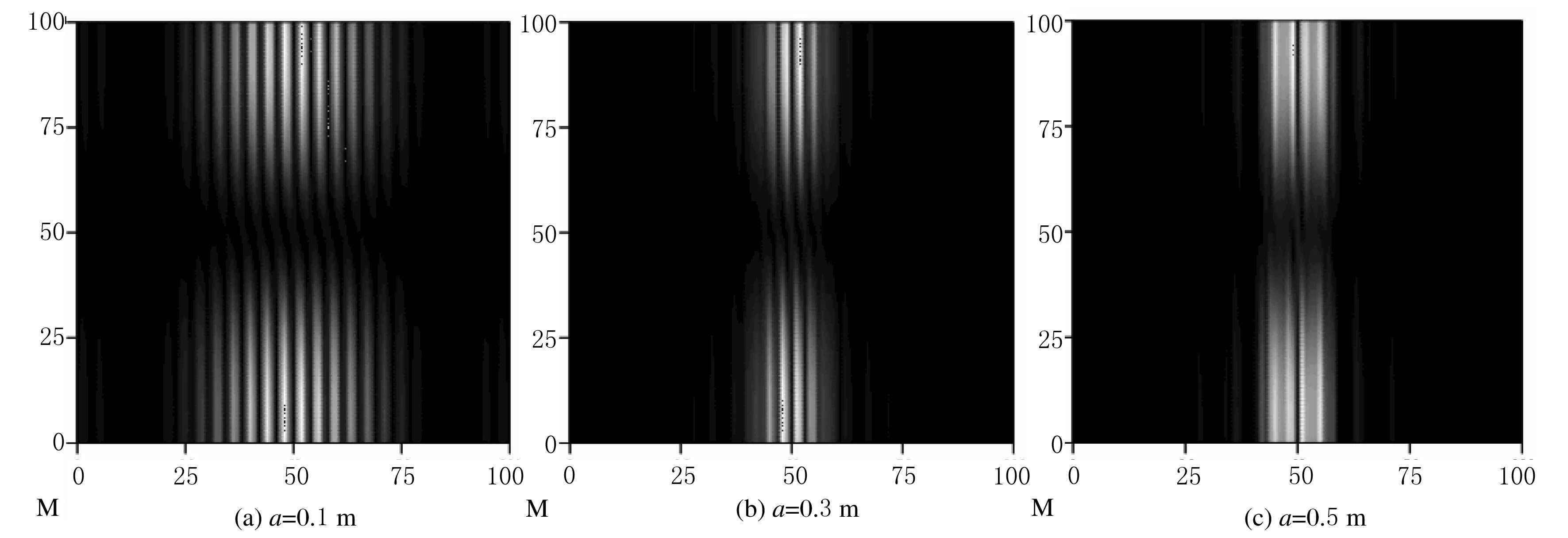
圖4 n=1，m=0.4 mm，z=1 m，σ=5 mm時,不同狹縫寬度的衍射圖樣

圖4討論了狹縫寬度對衍射條紋光強分布的影響.從圖4(a)～(c)可以看出，兩狹縫寬度越小，衍射條紋越清晰，且條紋數目越多，即條紋擴展度越大.由此判定，狹縫寬度越小，條紋擴展度越大，衍射現象越明顯.通過衍射條紋的擴展情況可以定性判斷衍射狹縫的寬窄.

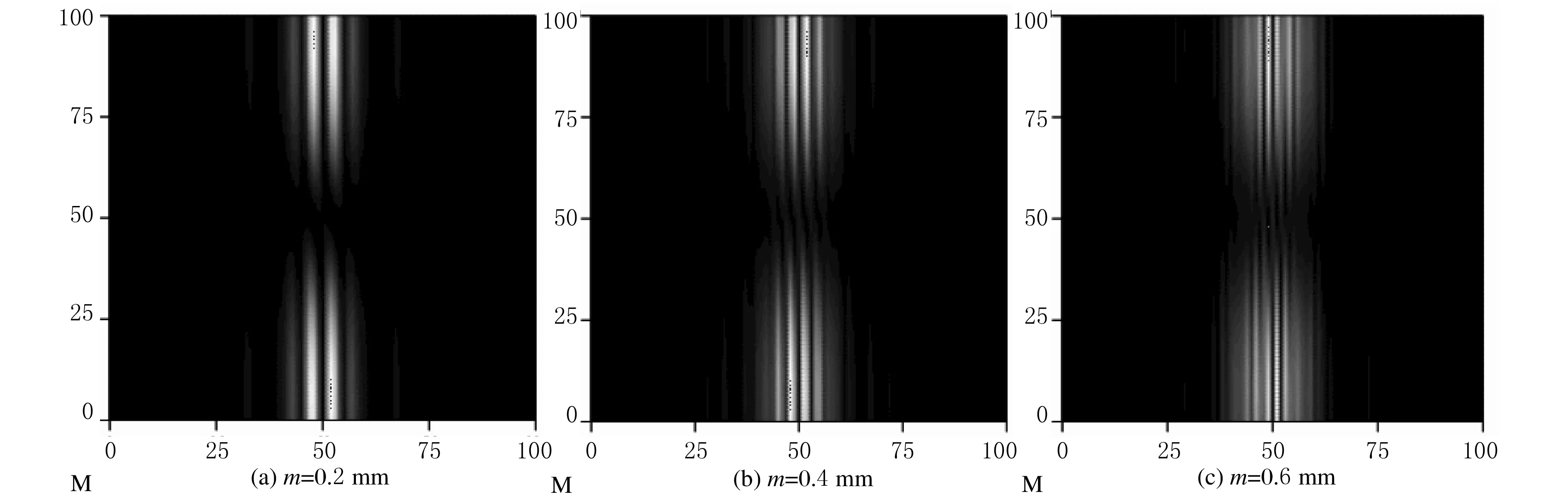
圖5 n=1，a1=a2=0.3 mm，z=1 m，σ=5 mm時,兩個狹縫間距值不同時的衍射圖樣

圖5討論了狹縫間距對衍射條紋光強分布的影響.圖5(a)～(c) 是狹縫間距分別為 2m=0.4 mm，2m=0.8 mm 和2m=1.2 mm時的衍射圖樣，圖中反映出狹縫間距越小，衍射條紋越清晰，即衍射現象越顯著.通過衍射現象的清晰度或顯著效應可以定性判斷狹縫間距的大小.

圖6 n=1，a1=a2=0.3 mm，m=0.4 mm，z=1 m,時，不同光斑大小的衍射圖樣

圖6討論了光斑大小對衍射條紋光強分布的影響.從圖6(a)～(c)可以看出，光斑越小，衍射條紋的可見度越大，即光斑大小與條紋的可見度成反比.由此可知通過衍射條紋可見度的相對大小定性判斷光斑的大小.

3 結論

討論了拉蓋爾-高斯渦旋光束通過雙縫衍射后在光場中的條紋分布情況，探究了拓撲荷值、衍射距離、狹縫寬度、狹縫間距、光斑大小對條紋形狀和光強的影響.結果表明，拉蓋爾-高斯渦旋光束的雙縫衍射圖樣是一組平行于狹縫的明暗交替分布的條紋，中央零級出現了兩條光強相等的主極大亮條紋，兩側次極大亮紋的光強隨著條紋級數的增加而逐漸減小.拓撲荷值的正負和大小對衍射條紋的形狀產生了一定的干擾；衍射距離跟條紋間距成正比；狹縫寬度越小，條紋的擴展度也越大，衍射現象越明顯；狹縫間距越小，衍射條紋越清晰；光斑越小，衍射條紋的可見度越大.