基于TensorFlow的深度神經(jīng)網(wǎng)絡(luò)優(yōu)化方法研究

王保敏，王 睿，阮進(jìn)軍，慈 尚

(安徽商貿(mào)職業(yè)技術(shù)學(xué)院 信息與人工智能學(xué)院,安徽 蕪湖 241002)

深度神經(jīng)網(wǎng)絡(luò)可以視為添加了若干個(gè)隱藏層的神經(jīng)網(wǎng)絡(luò)，它是感知機(jī)的拓展.感知機(jī)的基本結(jié)構(gòu)包括輸入層和輸出層，輸入層用于接收來自外界的信號(hào)，其模型如圖1所示.

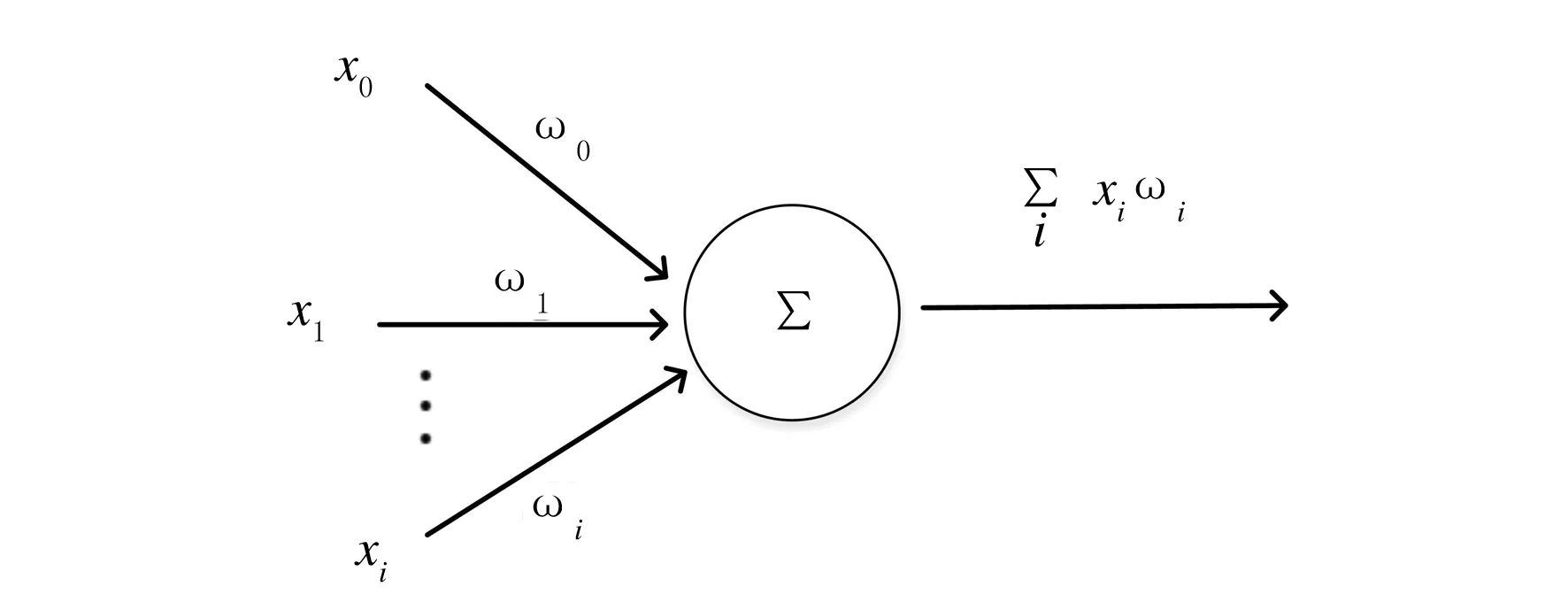
圖1 感知機(jī)模型結(jié)構(gòu)

感知機(jī)輸出和輸入之間的關(guān)系是線性的，經(jīng)過學(xué)習(xí)可得到的輸出結(jié)果為

(1)

經(jīng)過神經(jīng)元激活函數(shù)，可以得到最終的輸出結(jié)果為1或者-1[1]：

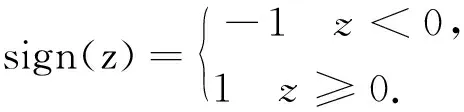
(2)

可以看出，一個(gè)簡(jiǎn)單的感知機(jī)模型能夠解決的僅僅是二分類問題.對(duì)于復(fù)雜的非線性模型，感知機(jī)模型無法通過學(xué)習(xí)得到理想的結(jié)果.隨著機(jī)器學(xué)習(xí)技術(shù)的發(fā)展，神經(jīng)網(wǎng)絡(luò)逐步替代了感知機(jī)，其對(duì)感知機(jī)模型做了3個(gè)方面的拓展：首先，在輸入和輸出之間增加了隱藏層，可以根據(jù)需要設(shè)計(jì)成多層結(jié)構(gòu)，從而增強(qiáng)了模型的表達(dá)能力；其次，輸出層的神經(jīng)元不再局限于兩個(gè)結(jié)果，而是可以為多個(gè)結(jié)果輸出，這樣模型可以靈活應(yīng)用于分類回歸以及其他機(jī)器學(xué)習(xí)領(lǐng)域的降維和聚類等問題；最后，神經(jīng)網(wǎng)絡(luò)對(duì)感知機(jī)的激活函數(shù)做了擴(kuò)展，可以是tanx、Softmax或者ReLU等，比如在Logistic回歸里面通常采用的是Sigmoid函數(shù)，即：f(x)=1/(1-e-x).不同的激活函數(shù)，在不同程度上都增強(qiáng)了神經(jīng)網(wǎng)絡(luò)的表達(dá)能力.

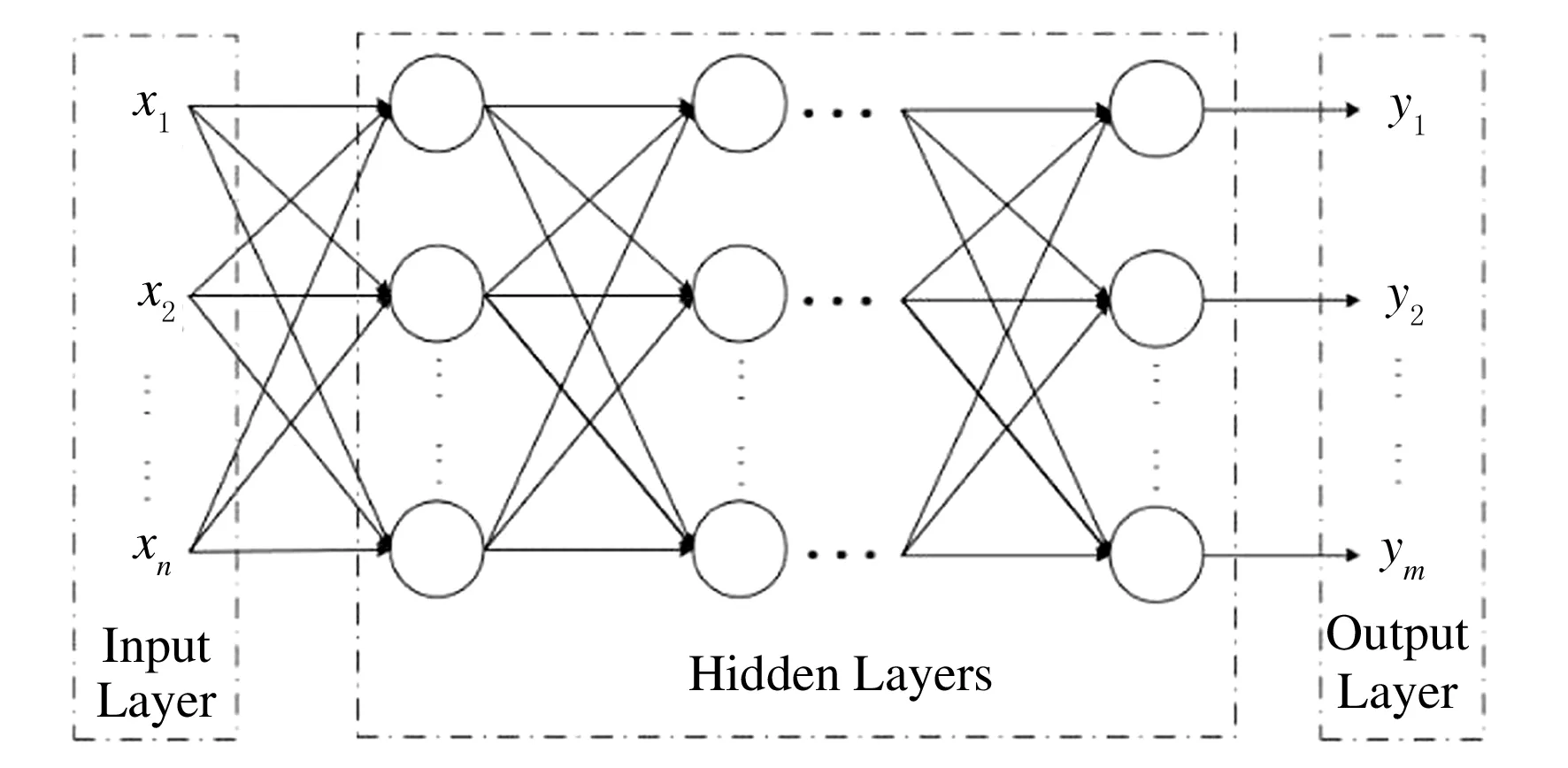
圖2 深度神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

從結(jié)構(gòu)上看，深度神經(jīng)網(wǎng)絡(luò)(Deep Neural Networks，DNN)是一個(gè)包含了多個(gè)隱藏層的網(wǎng)絡(luò),由輸入層、隱藏層和輸出層組成，層與層之間是全連接關(guān)系.雖然DNN內(nèi)部組成部分關(guān)聯(lián)性較大，但是從微觀范圍來看，基本與感知機(jī)類似，局部輸入和輸出之間是線性關(guān)系.從總體上看，DNN本質(zhì)上是一個(gè)非線性非凸函數(shù)[2]，其基本結(jié)構(gòu)如圖2所示.

1 問題分析

深度學(xué)習(xí)是一種基于特征的學(xué)習(xí)方法，而特征是通過學(xué)習(xí)過程從數(shù)據(jù)中提取出來的[3]，一般可以通過兩個(gè)步驟實(shí)現(xiàn)對(duì)神經(jīng)網(wǎng)絡(luò)的優(yōu)化.首先是通過前向傳播算法得到模型的輸出值(預(yù)測(cè)值)，同時(shí)計(jì)算輸出預(yù)測(cè)值和真實(shí)值的差值；其次利用BP(Back Propagation)算法求得損失函數(shù)對(duì)模型中每個(gè)參數(shù)的偏導(dǎo)數(shù)(梯度)，最終通過偏導(dǎo)數(shù)和學(xué)習(xí)率(learning rate)使用梯度下降算法迭代計(jì)算出各個(gè)參數(shù)的取值.

1.1 過擬合問題

在實(shí)際應(yīng)用場(chǎng)景中，并非僅僅是使用深度神經(jīng)網(wǎng)絡(luò)去模擬訓(xùn)練數(shù)據(jù)，而是通過訓(xùn)練，使得模型更加貼合實(shí)際從而最大程度地判斷未知數(shù)據(jù).判斷模型在未知數(shù)據(jù)中的性能，并不能完全根據(jù)其在訓(xùn)練數(shù)據(jù)上的表現(xiàn)結(jié)果，原因在于存在著過擬合問題.所謂過擬合，指的是當(dāng)模型復(fù)雜程度變高之后，雖然能夠較好地刻畫出訓(xùn)練數(shù)據(jù)中的隨機(jī)噪音，但是在挖掘和提煉訓(xùn)練數(shù)據(jù)中的通用規(guī)則或者特征等方面表現(xiàn)出了局限性.過擬合由于過度關(guān)注了訓(xùn)練數(shù)據(jù)中的噪音而忽視了問題的整體規(guī)律.

1.2 參數(shù)值突變問題

權(quán)重weight和偏差bias在神經(jīng)網(wǎng)絡(luò)模型訓(xùn)練過程中可能出現(xiàn)更新幅度過大或者過小，從而表現(xiàn)出參數(shù)值在迭代過程中出現(xiàn)“突變”現(xiàn)象，導(dǎo)致訓(xùn)練過程中遇到異常波動(dòng)狀況，降低了模型在未知數(shù)據(jù)上的健壯性.為便于說明這一問題，假設(shè)某個(gè)參數(shù)x在訓(xùn)練過程中得到了原始10個(gè)數(shù)值，用集合表示,記為x={-10,2,5,6,1,8,3,5,6,3,-1}，顯然可以看出這10個(gè)值存在較大的波動(dòng)性，尤其是-10作為參數(shù)將會(huì)是一個(gè)“噪音”，代入模型后，會(huì)對(duì)訓(xùn)練結(jié)果產(chǎn)生較大的干擾，不利于模型的訓(xùn)練效率和結(jié)果求解.

2 計(jì)算方法優(yōu)化

針對(duì)上述問題，本文分別引入了正則化思想解決過擬合問題，采用滑動(dòng)平均模型解決參數(shù)值突變問題，提高模型的訓(xùn)練效果.

2.1 正則化處理

為了優(yōu)化模型參數(shù)，避免過擬合問題，一個(gè)常用的方法是對(duì)模型進(jìn)行正則化(regularization)處理[4].正則化通過約束參數(shù)的范數(shù)來降低模型的復(fù)雜度，其基本方法是在損失函數(shù)中增加能夠表現(xiàn)模型復(fù)雜程度的附加項(xiàng)[5].假設(shè)模型中的損失函數(shù)為P(θ)，描述模型復(fù)雜程度的函數(shù)是Q(ω)，那么正則化處理的方式是：在優(yōu)化P(θ)的同時(shí)，優(yōu)化Q(ω)，即綜合優(yōu)化P(θ)+λQ(ω)，其中λ為模型復(fù)雜損失在總損失中的比重，θ代表神經(jīng)網(wǎng)絡(luò)模型中的所有參數(shù)，包括權(quán)值ω和偏移值b.通常模型復(fù)雜程度是由權(quán)重ω所決定.常用的描述模型復(fù)雜度的函數(shù)Q(ω)有兩種，一種是L1正則化，對(duì)ω取模后求和，計(jì)算公式為：

(3)

另一種是L2正則化，對(duì)ω平方取模后求和，計(jì)算公式為：

(4)

公式(3)和(4)中ωi表示模型中第i個(gè)權(quán)重參數(shù).上述兩種正則化方法的思想都是試圖通過限制模型中權(quán)值的大小來減少擬合訓(xùn)練數(shù)據(jù)過程中出現(xiàn)的隨機(jī)噪音，但L1正則化和L2正則化是存在很大差異的.L1正則化可以讓參數(shù)在訓(xùn)練過程中變?yōu)?，顯示出更稀疏的性質(zhì)，從而有利于模型類似特征的選取.L2正則化避免了這種情況的出現(xiàn)，因?yàn)楫?dāng)參數(shù)取值很小時(shí)，其平方更小以至于可以忽略，且L2正則化公式是可導(dǎo)的，在優(yōu)化時(shí)會(huì)令求損失函數(shù)的偏導(dǎo)變得更加簡(jiǎn)潔.在實(shí)際應(yīng)用中，可以同時(shí)使用L1正則化和L2正則化：

(5)

其中：α為L(zhǎng)1正則化項(xiàng)所占系數(shù).

2.2 指數(shù)移動(dòng)平均模型

在神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程中，為了使模型結(jié)果不發(fā)生突變，參數(shù)更新幅度不能過大或者過小，且更新后的參數(shù)值與之前的參數(shù)值需要有關(guān)聯(lián)，要盡量避免異常的參數(shù)值，即使遇到一些突變的數(shù)值，也需要對(duì)其進(jìn)行抑制，從而保障模型的魯棒性.為解決參數(shù)值突變問題，在模型中采用了指數(shù)移動(dòng)平均算法(Exponential Moving Average, EMA)，對(duì)不同階段的權(quán)重進(jìn)行平滑處理，以此來預(yù)測(cè)未知事物趨勢(shì)[7]，從而在一定程度上提高模型在測(cè)試數(shù)據(jù)集上的表現(xiàn).

滑動(dòng)平均模型的基本思想是對(duì)每個(gè)變量αt維護(hù)一個(gè)影子變量vt，vt與αt的初始值相同，在每次更新變量αt時(shí)，影子變量vt的值也做相應(yīng)調(diào)整，被設(shè)置為：

vt=vt-1·β+αt·(1-β)，

(6)

其中：β為衰減率，決定模型參數(shù)的更新速度.從滑動(dòng)平均模型與深度學(xué)習(xí)的關(guān)系來看，使用滑動(dòng)平均模型可令整體參數(shù)數(shù)據(jù)更加平滑，屏蔽了數(shù)據(jù)噪音，杜絕了異常值的出現(xiàn).

3 基于TensorFlow的優(yōu)化方法實(shí)現(xiàn)

3.1 正則化處理方法實(shí)現(xiàn)

TensorFlow是由Google開發(fā)的一種開源框架，借助其強(qiáng)大的深度學(xué)習(xí)功能，能夠高效進(jìn)行高性能數(shù)值計(jì)算[8].在TensorFlow中，損失函數(shù)可以加入正則化的部分，代碼如下：

loss=tf.reduce_mean(tf.square(y_-y))

tf.contrib.layers.l2_regularizer(lambda)(w)

以上代碼中，loss為損失函數(shù)，它包含兩個(gè)部分，分別是用于衡量模型在訓(xùn)練數(shù)據(jù)集上表現(xiàn)效果的均方誤差損失函數(shù)，以及抑制隨機(jī)噪音出現(xiàn)的正則化項(xiàng).TensorFlow提供tf.contrib.layers.l1_regularizer()函數(shù)計(jì)算L1的值，tf.contrib.layers.l2_regularizer()計(jì)算L2正則化項(xiàng)的值.在簡(jiǎn)單的神經(jīng)網(wǎng)絡(luò)中，這樣可以很好地計(jì)算包含正則化項(xiàng)的損失函數(shù).

3.2 指數(shù)移動(dòng)平均模型實(shí)現(xiàn)

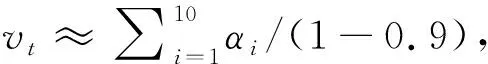
定義變量v1，其類型為tf.float32，初始值是0，用以計(jì)算指數(shù)移動(dòng)平均值：

v1=tf.Variable(0,dtype=tf.float32)

定義變量step，表示神經(jīng)網(wǎng)絡(luò)中選代的輪數(shù)，其作用是用以動(dòng)態(tài)控制衰減率：

step=tf.Variable(0,trainable=False)

定義類(class)來計(jì)算指數(shù)移動(dòng)平均值,其中0.98為初始化時(shí)的衰減因子：

ema = tf.train.ExponentialMovingAverage(0.98, step)

定義一個(gè)操作用來更新變量的滑動(dòng)平均值，需要傳入的參數(shù)是一個(gè)變量列表，每執(zhí)行一次操作列表中的變量將同時(shí)更新一次：

maintain_average_op=ema.apply([v1])

4 實(shí)驗(yàn)與結(jié)果分析

為驗(yàn)證正則化處理和采用滑動(dòng)平均模型的效果，本文在MNIST數(shù)據(jù)集上實(shí)現(xiàn)了神經(jīng)網(wǎng)絡(luò)優(yōu)化算法，識(shí)別數(shù)據(jù)集上的手寫數(shù)字[9].

對(duì)MNIST數(shù)據(jù)集中的每張圖片，像素矩陣大小為28*28，在TensorFlow中為方便輸入，將其處理為一個(gè)長(zhǎng)度等于784的一維數(shù)組，即輸入層的節(jié)點(diǎn)數(shù)為784，輸出層的節(jié)點(diǎn)數(shù)為10(代表0到9).此外模型的基本參數(shù)設(shè)定如下：隱藏層節(jié)點(diǎn)數(shù)為500，基礎(chǔ)學(xué)習(xí)率為0.5，學(xué)習(xí)率的衰減率為0.99，正則化項(xiàng)在損失函數(shù)中的比重為0.001，訓(xùn)練輪數(shù)為50 000，滑動(dòng)平均衰減率為0.98.有關(guān)正則化損失函數(shù)和指數(shù)學(xué)習(xí)率設(shè)置的說明和代碼如下.

創(chuàng)建正則化函數(shù)regularizer：

regularizer = tf.contrib.layers.l2_regularizer(REGULARIZATION_RATE)

定義需要正則化處理的項(xiàng)regularization(其中weights1為從輸入層到隱藏層的權(quán)重參數(shù)，weights2為從隱藏層到輸出層的權(quán)重參數(shù))：

regularization = regularizer(weights1) + regularizer(weights2)

定義損失函數(shù)loss(由交叉熵cross_entropy_mean和正則化損失regularization兩部分組成)：

loss=cross_entropy_mean + regularization

設(shè)置指數(shù)衰減型學(xué)習(xí)率learning_rate(其中基礎(chǔ)學(xué)習(xí)率LEARNING_RATE_BASE為常量0.5，global_step為訓(xùn)練輪數(shù)，每次訓(xùn)練使用的樣本數(shù)BATCH_SIZE為常量100，滑動(dòng)平均衰減率LEARNING_RATE_DECAY為常量0.98)：

learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE,global_step,mnist.train.num_examples/BATCH_SIZE,LEARNING_RATE_DECAY)

定義訓(xùn)練步驟train_step(采用梯度下降優(yōu)化器GradientDescentOptimizer實(shí)現(xiàn)損失函數(shù)loss最小化)：

train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step=global_step)

優(yōu)化前后，訓(xùn)練輪數(shù)與正確率之間的關(guān)系曲線如圖3所示.

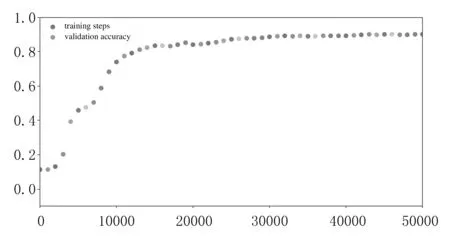
(a)優(yōu)化前

(b)優(yōu)化后 圖3 訓(xùn)練輪數(shù)與識(shí)別正確率關(guān)系曲線

由圖3可以看出，相比優(yōu)化前，優(yōu)化后的訓(xùn)練模型曲線更加平滑，這一趨勢(shì)在訓(xùn)練輪數(shù)為10 000至20 000區(qū)間內(nèi)表現(xiàn)尤為明顯，顯示出較高的性能.其次，從正確率上看，經(jīng)過50 000輪訓(xùn)練，說明優(yōu)化效果更好.

5 結(jié)論

隨著計(jì)算機(jī)硬件性能和計(jì)算能力的提升，深度神經(jīng)網(wǎng)絡(luò)被廣泛應(yīng)用于語音識(shí)別和圖形圖像識(shí)別，其識(shí)別準(zhǔn)確率和速率大大超過了人類.本文使用正則化和指數(shù)滑動(dòng)平均算法能夠優(yōu)化模型的訓(xùn)練參數(shù)[10]，能夠有效避免過擬合問題，降低數(shù)據(jù)“噪音”對(duì)模型訓(xùn)練的影響.